что такое ряд распределения
1. Статистические ряды распределения
1. Статистические ряды распределения
В результате обработки и систематизации первичных данных статистического наблюдения получают группировки, называемые рядами распределения.
Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку.
Различают атрибутивные и вариационные ряды распределения.
Атрибутивный – это ряд распределения, построенный по качественным признакам. Он характеризует состав совокупности по различным существенным признакам.
По количественному признаку строится вариационный ряд распределения. Он состоит из частоты (численности) отдельных вариантов или каждой группы вариационного ряда. Данные числа показывают, насколько часто встречаются различные варианты (значения признака) в ряду распределения. Сумма всех частот определяет численность всей совокупности.
В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды распределения. В дискретном вариационном ряде распределения группы составлены по признаку, изменяющемуся дискретно и принимающему только целые значения.
В интервальном вариационном ряде распределения группиро–вочный признак, составляющий основание группировки, может принимать в определенном интервале любые значения.
Вариационные ряды состоят из двух элементов: частоты и варианты.
Вариантой называют отдельное значение варьируемого признака, которое он принимает в ряду распределения.
Частота – это численность отдельных вариант или каждой группы вариационного ряда. Если частоты выражены в долях единицы или в процентах к итогу, то их называют частостями.
Правила и принципы построения интервальных рядов распределения строятся по аналогичным правилам и принципам построения статистических группировок. Если интервальный вариационный ряд распределения построен с равными интервалами, частоты позволяют судить о степени заполнения интервала единицами совокупности. Для проведения сравнительного анализа заполненности интервалов определяют показатель, который будет характеризовать плотность распределения.
Плотность распределения – это отношение числа единиц совокупности к ширине интервала.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
15. Статистические таблицы
15. Статистические таблицы Статистическая таблица – таблица, которая дает количественную характеристику статистической совокупности и представляет собой форму наглядного изложения полученных в результате статистической сводки и группировки числовых (цифровых)
19. Статистические карты
19. Статистические карты Статистические карты представляют собой вид графических изображений статистических данных на схематичной географической карте, характеризую–щих уровень или степень распространения того или иного явления на определенной территории.
38. Ряды агрегатных индексов с постоянными и переменными весами
38. Ряды агрегатных индексов с постоянными и переменными весами При изучении динамики экономических явл* ний строятся и исчисляются индексы за ряд последов тельных периодов. Они образуют ряды либо бази ных, либо цепных индексов. В ряду базисных индексе сравнение
6. Статистические термины
6. Статистические термины Статистическая информация, получаемая в результате наблюдения, необходима для предоставления органам государственного управления, для обеспечения информацией руководителей предприятий, компаний и т. д., для информирования общественности об
44. Статистические методы
44. Статистические методы Особенно широко используются статистические методы при изучении финансовых инвестиций. В основе изучения финансовых инвестиций лежит построение уравнения эквивалентности, так называемого баланса финансовой операции. Содержание данного
45. Статистические модели
45. Статистические модели Для эффективной работы на фондовом рынке необходимо знать, как доходность конкретного наименования акций (или портфеля акций конкретного инвестора) связана со средней рыночной доходностью всей совокупности акций, т. е. с рыночным индексом. Для
3. Статистические таблицы
3. Статистические таблицы После того как данные статистического наблюдения собраны и даже сгруппированы, их трудно воспринимать и анализировать без определенной, наглядной систематизации. Результаты статистических сводок и группировок получают оформление в виде
4. Ряды агрегатных индексов с постоянными и переменными весами
4. Ряды агрегатных индексов с постоянными и переменными весами При изучении динамики экономических явлений строятся и исчисляются индексы за ряд последовательных периодов. Они образуют ряды либо базисных, либо цепных индексов. В ряду базисных индексов сравнение
18. Статистические ряды распределения и их графическое изображение
18. Статистические ряды распределения и их графическое изображение Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку.Различают атрибутивные и вариационные ряды
19. Статистические таблицы
19. Статистические таблицы В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения.Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица
Статистические методы
Статистические методы Подсчет в толпе. Метод, честно говоря, наивный, но очень популярный. Организатор ресторанного бизнеса берет блокнот и карандаш, становится у двери похожего заведения в равноценном районе и считает, сколько человек проходит мимо в единицу времени.
1. Статистические ряды распределения
1. Статистические ряды распределения В результате обработки и систематизации первичных данных статистического наблюдения получают группировки, называемые рядами распределения.Статистические ряды распределения представляют собой упорядоченное расположение единиц
3. Статистические таблицы
3. Статистические таблицы В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения.Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица
ЛЕКЦИЯ № 10. Ряды динамики и их изучение в коммерческой деятельности
ЛЕКЦИЯ № 10. Ряды динамики и их изучение в коммерческой деятельности 1. Основные понятия о рядах динамики Все процессы и явления, протекающие в общественной жизни человека, являются предметом изучения статистической науки они находятся в постоянном движении и
Глава 6 АНГЛО-АМЕРИКАНЦЫ СМЫКАЮТ РЯДЫ
Международные статистические данные
Международные статистические данные Интернет существенно упростил сбор данных в мировом масштабе. В большинстве развитых и многих развивающихся странах обеспечен интернет-доступ к статистической информации. В свободном доступе размещают свои данные и международные
Ряды распределения, их виды



В результате сводки и группировки статистических данных получают ряды распределения.
Ряд распределения – это ряд чисел, характеризующий распределение единиц изучаемой совокупности по какому-либо признаку, причем значения признака расположены упорядоченно – в порядке возрастания либо убывания.
Ряды распределения подразделяются на следующие виды:
· атрибутивные ряды распределения;
· вариационные ряды распределения.
Атрибутивные ряды распределения образованы по атрибутивным, то есть качественным, признакам. Например, распределение населения по полу, по образованию и т.д. Атрибутивные признаки мы рассмотрели в параграфе 1.4.2. В атрибутивном ряду образуется столько групп, сколько наименований имеет данный атрибутивный признак. Например, в распределении населения по полу возможны только два типа признака: мужской и женский пол. Пример атрибутивного ряда распределения приведен в таблице 5.
Вариационные ряды распределения образуются по количественному признаку. Количественные признаки мы также рассмотрели в параграфе 4.2.
В вариационном ряду различают два элемента: варианты и частоты. Варианта – это отдельное значение признака в вариационном ряду. Варианты показываются в первой графе таблицы. Частота – это число, показывающее, как часто повторяется та или иная варианта. Значений частот столько, сколько вариант в данном ряду. Каждой варианте соответствует своя частота.
Различают такие вариационные ряды распределения:
В дискретных вариационных рядах признак изменяется прерывно, принимает отдельные целые значения. Пример приведен в таблице 7.
Таблица 7 – Распределение рабочих организации по квалифиции
| Разряд | Количество рабочих, чел. |
| Итого |
Данный ряд распределения является дискретным вариационным, так как признак (разряд) – количественный, выражается отдельными целыми числами, которые расположены в порядке возрастания.
В интервальных вариационных рядах значения вариант задаются в виде интервалов. Виды интервалов и правила их построения мы изучили в параграфе 1.4.2. Примеры интервального вариационного ряда приведены в таблицах 2, 3, 8.
Таблица 8 – Распределение работников организации по стажу работы
| Стаж работы, лет | Количество работников, чел. |
| от 0 до 5 | |
| от 5 до 10 | |
| от 10 до 15 | |
| от 15 до 20 | |
| от 20 до 25 | |
| свыше 25 | |
| Итого |
Данный ряд распределения является интервальным вариационным, так как признак (стаж) – количественный, выражается множеством как целых, так и дробных чисел, которые сгруппированы в интервалы и расположены в порядке возрастания. Интервалы – равные, закрытые, кроме последнего. Последний интервал – открытый.
Сводка и группировка статистических данных
3.3. Ряды распределения: виды, правила построения, графическое изображение
Ряды распределения делятся на атрибутивные и вариационные, в зависимости от признака, положенного в основу группировки. Если признак качественный, то ряд распределения называется атрибутивным. Примером атрибутивного ряда является распределение предприятий и организаций по формам собственности (см. табл. 3.1).
Если признак, по которому строится ряд распределения, количественный, то ряд называется вариационным.
Вариационные ряды бывают дискретными и интервальными. У дискретных рядов (табл. 3.7) варианты выражены конкретными числами, чаще всего целыми.
| Время работы в компании, полных лет (варианты) | Число работающих | |
|---|---|---|
| Человек (частоты) | в % к итогу (частости) | |
| до года | 15 | 11,6 |
| 1 | 17 | 13,2 |
| 2 | 19 | 14,7 |
| 3 | 26 | 20,2 |
| 4 | 10 | 7,8 |
| 5 | 18 | 13,9 |
| 6 | 24 | 18,6 |
| Итого | 129 | 100,0 |
Если признак принимает ограниченное число значений, обычно не больше 10, строят дискретные ряды распределения. Если вариант больше, то дискретный ряд теряет свою наглядность; в этом случае целесообразно использовать интервальную форму вариационного ряда. При непрерывной вариации признака, когда его значения в определенных пределах отличаются друг от друга на сколь угодно малую величину, также строят интервальный ряд распределения.
3.3.1. Построение дискретных вариационных рядов
Рассмотрим методику построения дискретных вариационных рядов на примере.
Пример 3.2. Имеются следующие данные о количественном составе 60 семей:
| 2 3 3 1 4 2 3 3 1 5 2 4 3 2 2 1 2 3 4 5 |
| 2 2 1 3 4 3 3 3 6 6 3 3 6 1 3 4 3 4 4 5 |
| 3 3 2 2 1 3 2 5 5 2 4 3 6 1 2 2 3 1 3 4 |
Для того чтобы получить представление о распределении семей по числу их членов, следует построить вариационный ряд. Поскольку признак принимает ограниченное число целых значений строим дискретный вариационный ряд. Для этого сначала рекомендуется выписать все значения признака (число членов в семье) в порядке возрастания (т.е. провести ранжирование статистических данных):
| 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 |
| 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 |
| 3 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 |
| Число членов семьи (х) | Число семей (y) |
|---|---|
| 1 | 8 |
| 2 | 14 |
| 3 | 20 |
| 4 | 9 |
| 5 | 5 |
| 6 | 4 |
| Итого | 60 |
3.3.2. Построение интервальных вариационных рядов
Покажем методику построения интервальных вариационных рядов распределения на следующем примере.
Пример 3.3. В результате статистического наблюдения получены следующие данные о средней величине процентной ставки 50 коммерческих банков (%):
| 14,7 | 19,0 | 24,5 | 20,8 | 12,3 | 24,6 | 17,0 | 14,2 | 19,7 | 18,8 |
| 18,1 | 20,5 | 21,0 | 20,7 | 20,4 | 14,7 | 25,1 | 22,7 | 19,0 | 19,6 |
| 19,0 | 18,9 | 17,4 | 20,0 | 13,8 | 25,6 | 13,0 | 19,0 | 18,7 | 21,1 |
| 13,3 | 20,7 | 15,2 | 19,9 | 21,9 | 16,0 | 16,9 | 15,3 | 21,4 | 20,4 |
| 12,8 | 20,8 | 14,3 | 18,0 | 15,1 | 23,8 | 18,5 | 14,4 | 14,4 | 21,0 |
Как видим, просматривать такой массив данных крайне неудобно, кроме того, не видно закономерностей изменения показателя. Построим интервальный ряд распределения.
Число интервалов на практике часто задается самим исследователем исходя из задач каждого конкретного наблюдения. Вместе с тем его можно вычислить и математически по формуле Стерджесса
Для нашего примера получим: n = 1 + 3,322lgN = 1 + 3,322lg50 = 6,6 » 7.
Для нашего примера
Интервалы вариационного ряда наглядны, если их границы имеют «круглые» значения, поэтому округлим величину интервала 1,9 до 2, а минимальное значение признака 12,3 до 12,0.
Интервалы, как правило, записывают таким образом, чтобы верхняя граница одного интервала являлась одновременно нижней границей следующего интервала. Так, для нашего примера получим: 12,0-14,0; 14,0-16,0; 16,0-18,0; 18,0-20,0; 20,0-22,0; 22,0-24,0; 24,0-26,0.
Подобная запись означает, что признак непрерывный. Если же варианты признака принимают строго определенные значения, например, только целые, но их количество слишком велико для построения дискретного ряда, то можно создать интервальный ряд, где нижняя граница интервала не будет совпадать с верхней границей следующего интервала (это будет означать, что признак дискретный). Например, в распределении работников предприятия по возрасту можно создать следующие интервальные группы лет: 18-25, 26-33, 34-41, 42-49, 50-57, 58-65, 66 и более.
Кроме того, в нашем примере мы могли бы сделать первый и последний интервалы открытыми, т.д. записать: до 14,0; 24,0 и выше.
| Ставка банка % (варианты) | |||
|---|---|---|---|
| 12,3 | 17,0 | 19,9 | 23,8 |
| 12,8 | 17,4 | 20,0 | 24,5 |
| 13,0 | 18,0 | 20,0 | 24,6 |
| 13,3 | 18,1 | 20,4 | 25,1 |
| 13,8 | 18,5 | 20,4 | 25,6 |
| 14,2 | 18,7 | 20,5 | |
| 14,3 | 18,8 | 20,7 | |
| 14,4 | 18,9 | 20,7 | |
| 14,7 | 19,0 | 20,8 | |
| 14,7 | 19,0 | 21,0 | |
| 15,1 | 19,0 | 21,0 | |
| 15,2 | 19,0 | 21,1 | |
| 15,3 | 19,0 | 21,4 | |
| 16,0 | 19,6 | 21,9 | |
| 16,9 | 19,7 | 22,7 | |
При подсчете частот может возникнуть ситуация, когда значение признака попадет на границу какого-либо интервала. В таком случае можно руководствоваться правилом: данная единица приписывается к тому интервалу, для которого ее значение является верхней границей. Так, значение 16,0 в нашем примере будет относиться ко второму интервалу.
Результаты группировки, полученные в нашем примере, оформим в таблице.
| Краткая ставка, % | Количество банков, ед. (частоты) | Накопленные частоты |
|---|---|---|
| 12,0-14,0 | 5 | 5 |
| 14,0-16,0 | 9 | 14 |
| 16,0-18,0 | 4 | 18 |
| 18,0-20,0 | 15 | 33 |
| 20,0-22,0 | 11 | 44 |
| 22,0-24,0 | 2 | 46 |
| 24,0-26,0 | 4 | 50 |
| Итого | 50 | — |
В процессе группировки данных при построении вариационных рядов иногда используются неравные интервалы. Это относится к тем случаям, когда значения признака подчиняются правилу арифметической или геометрической прогрессии или когда применение формулы Стерджесса приводит к появлению «пустых» интервальных групп, не содержащих ни одной единицы наблюдения. Тогда границы интервалов задаются произвольно самим исследователем исходя из здравого смысла и целей обследования либо по формулам. Так, для данных, изменяющихся в арифметической прогрессии, величина интервалов вычисляется следующим образом:
Порядок расчетов границ неравных интервалов для данных, изменяющихся приблизительно в арифметической прогрессии, показан в табл. 3.15.
Для показателей, приблизительно изменяющихся в геометрической прогрессии, величину интервалов можно вычислить по формуле
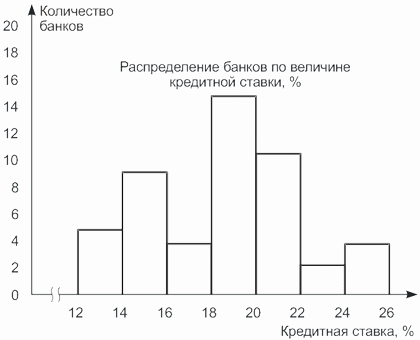
Для графического изображения интервального ряда используют гистограмму, имеющую вид многоступенчатой фигуры, состоящей из прямоугольников. По оси абсцисс откладывают значения границ интервалов. Сами интервалы будут являться основаниями прямоугольников. Высота прямоугольников соответствует частоте или частости интервалов, которые откладываются по оси ординат.
По данным таблицы, приведенной в примере 3.3, построим гистограмму (рис. 3.2).
При неравных интервалах у гистограммы распределения высотами прямоугольников будут являться показатели плотности распределения, рассчитываемые как частное от деления частоты интервала на его величину.
Зависимость между значениями признака и накопленными частотами показывают особые графики, называемые кумулятой и огивой распределения.
В случае интервального ряда при построении кумуляты по оси абсцисс отмечают границы интервальных групп, накопленные частоты по оси ординат относят к верхним границам интервалов.
По данным таблицы, приведенной в примере 3.3, построим кумуляту распределения для интервального ряда (рис. 3.2).
Если у кумулятивной кривой поменять местами ось абсцисс с осью ординат, получим график, называемый огивой распределения (рис. 3.4).