что такое ряд чисел фибоначчи

Что такое числа Фибоначчи и уровни Фибоначчи

Последовательность Фибоначчи это набор чисел (и проистекающих из них пропорций), который постоянно встречается в окружающей нас природе. Открытие этого явления приписывают математику 13-го века, Леонардо Фибоначчи.

В данной последовательности каждый член равен сумме двух предыдущих:

Используя эту формулу, и предполагая, что первые две цифры ноль и единица, можно вычислить первые десять чисел последовательности следующим образом:

Таким образом, первые десять чисел в последовательности Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.

Количество лепестков на цветах часто совпадает с числами Фибоначчи, особенно 3, 5 и 8. Некоторые ромашки имеют 13 и 21 лепестков.

Коэффициенты Фибоначчи

Из последовательности Фибоначчи выводится ряд коэффициентов имеющих особое значение для трейдеров.

Наиболее важным коэффициентом является отношение очередного члена последовательности к следующему члену. Это соотношение практически одинаково для любых двух последовательно идущих членов и стремится к величине 0,618 или 61,8%. Это соотношение называют «золотой серединой» или «золотым сечением». Золотое сечение также имеет широкое распространение в природе, в частности пропорции человеческого тела, очень близки к нему. В трейдинге значение 61,8% является наиболее надежным уровнем прогнозирования отката. Например:

8 разделить на 13 = 0,615 = 61,5%

13 разделить на 21 = 0,619 = 61,9%

21 разделить на 34 = 0.617 = 61,7%

Два других коэффициента Фибоначчи часто используемые трейдерами это 38,2% и 23,6%. Эти два коэффициента считаются менее надежными, но также применяются в техническом анализе.

Отношение 38,2% получают путем деления любого члена последовательности на число стоящее через один разряд вправо. Например:

8 делится на 21 = 0,380 = 38,0%

144 делится на 377 = 0,381 = 38,1%

6765 делится на 17 716 = 0,381 = 38,1%

Аналогичным образом, отношение 23,6% получается делением любого члена последовательности на число через два разряда вправо:

5 делится на 21 = 0,238 = 23,8%

34 разделить на 144 = 0,236 = 23,6%

6765 делится на 28 667 = 0,235 = 23,5%

Кликните по рисунку для увеличения

Практическое использование в трейдинге

Многие трейдеры уверены в том, что ценовое движение действительно подчиняется определённым ритмам и законам задаваемым последовательностью чисел и коэффициентов Фибоначчи, но есть и не мало противников данной теории.

Уверенность сторонников теории Фибонначи базируется на том, что рынок, являясь, по сути, одним из продуктов человеческой деятельности (а следовательно имеет прямую зависимость от природы человека), также подчиняется тем глобальным законам, которые характерны для природы в целом.

Считается, что первым кто обратил внимание на зависимость циклов ценовых движений от коэффициентов Фибоначчи, был американец Ральф Эллиот (создавший впоследствии на их основе теорию названную его именем). Он исследовал множество ценовых графиков за различные периоды времени и пришёл к выводу о том, что движение цены происходит волнообразно, при этом существуют волны большего и меньшего порядков отличающиеся друг от друга в пропорциях вытекающих из чисел последовательности Фибоначчи.

Заметьте, что Ральф Эллиот проводил свои исследования в 30-х годах прошлого века, когда не о каких компьютерах не было и речи. Каждый график требовалось отрисовывать и анализировать вручную. С развитием же современной компьютерной техники, возможность анализировать множество ценовых графиков на самых разных временных промежутках появилась у каждого трейдера имеющего в своём распоряжении мало-мальски приличный торговый терминал (например, тот же самый МТ4).

Числа, уровни и коэффициенты Фибоначчи на ценовых графиках

Давайте рассмотрим весь арсенал инструментов технического анализа основанных на применении чисел последовательности Фибоначчи. Ввиду большой популярности у трейдеров, все эти инструменты нашли своё отражение в современных торговых терминалах. Я покажу вам их на примере одного из самых распространённых терминалов — Мetatrader4 (МТ4).

Здесь их можно найти в меню «Insert» («Вставка») в разделе «Fibonacci»:

А кроме этого, здесь есть ещё и канальный индикатор на основе этих чисел. Его можно найти в разделе «Channels»:

Линии (Retracement)

Для построения на ценовом графике линий Фибоначчи вам нужно найти две базовые точки являющие собой два важных экстремума (в идеале — большой волны тренда). Соединив эти точки между собой вы получите шесть уровней от 0 до 100%.

Крайние из этих уровней (0% и 100%) будут соответствовать тем точкам, которые были выбраны в качестве базовых. А остальные четыре уровня: 23.6%, 38.2%, 50%, 61.8% будут показывать вероятные места разворотов и пределы откатов ценового движения.

Подробности построения и детали использования линий Фибоначчи изложены в материале: «Линии Фибоначчи. Построение, настройка и пример использования»

Временные зоны (Time Zones)

Точки разворота цены на графиках имеют две координаты. Одна из этих координат лежит на вертикальной оси (цены) и определяется горизонтальными уровнями на графике. Другая из координат находится на горизонтальной шкале времени. Временные зоны Фибоначчи как раз используются для того, чтобы определить эти самые вторые координаты важных разворотных точек на ценовом графике.

Для построения временных зон достаточно также выбрать два важных ценовых экстремума на графике.

Обратите внимание на то, как точно построенные временные зоны указывают на важные разворотные моменты графика. Более подробную информацию ищите здесь: «Временные зоны Фибоначчи. Как их установить и как правильно использовать»

Веер (Fan)

Также как и при построении вышеописанных инструментов, для того чтобы отобразить веер Фибоначчи на ценовом графике необходимо выбрать две базовые точки (например в виде экстремумов очередной волны тренда).

После этого на графике построится веер с вершиной в первой точке и тремя лучами соответствующими коэффициентам 38.2, 50.0, 60.8.

Как видите, последующие разворотные точки довольно точно накладываются на лучи построенного веера. Более подробно о веере вы можете прочитать здесь: «Веер Фибоначчи. Как установить, настроить и правильно использовать»

Дуги (Arcs)

Дуги также строятся на основе двух базовых точек, и таким же образом показывают наиболее вероятные границы на которых будут происходить развороты цены. Визуально они представляют собой три эллипса построенные по коэффициентам 38.2, 50.0, 60.8

Расширение (Expansion)

Для построения расширений Фибоначчи требуется уже не две, а три базовых точки. А в остальном они очень схожи с линиями Фибоначчи описанными выше. Базовые точки выбираются на экстремумах очередной волны тренда.

На восходящем тренде (как на рисунке выше) первая точка ставится на минимуме волны, вторая — на максимуме, а третья — на следующем минимуме (находящемся выше предыдущего). В случае нисходящего тренда первую точку ставим на максимуме волны, вторую — на следующем за ним минимуме и третью — на новом максимуме (который находится ниже предыдущего).

Как видно из представленного рисунка и здесь тоже развороты цены достаточно часто совпадают с уровнями заданными расширениями. Подробности по этому инструменту можно найти здесь: «Расширение Фибоначчи. Установка, настройка и использование»

Источник

Числа Фибоначчи: что это, кто открыл и где применимо. Число Фибоначчи в науке и искусстве

Фибоначчи ― числа, которые следуют друг за другом. При этом сумма двух очередных слагаемых равна сумме двух предыдущих. Например:

13 = 5 + 8, и так до бесконечности.

Название «числа Фибоначчи» было взято от прозвища математика Леонардо Пизанского, жившего в средние века в Италии. Буквально переводится как «рожден хороший сын». По двум другим версиям, означает «Боначчо» и «удачливый».

Как было сделано открытие?

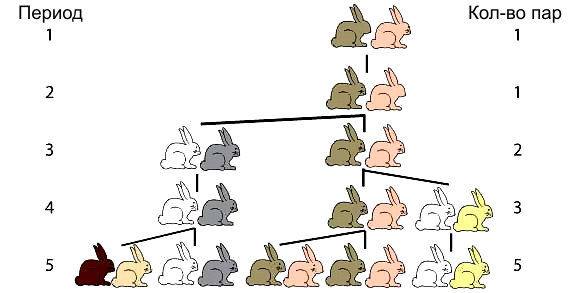
Средневековый математик Леонардо Пизанский привел последовательность чисел согласно числовой очередности в задаче о размножении кроликов. При условии, что вначале были самец и самка, и никто из рожденных не умирал, то за 12 месяцев животных становится 233 пары. О своем открытии ученый написал в научном труде «Книга Абака».

Но еще до того как была озвучена эта методика, древние инки пользовались ею при подсчете и минимизации количества зерен.

Числа Фибоначчи в природе

Где в окружающем мире встречаются числа Фибоначчи:

семена в корзине подсолнечника;

Так, фрактал, или подобие себя, увеличиваясь, сохраняет ту же форму. Благодаря ему создается максимально компактная структура с четким рисунком, под определенным углом — 137,5°. Это значит, например, что растущие под таким углом листья располагаются по спирали и не мешают росту других листков.

Число Фибоначчи в науке и искусстве

Число Фибоначчи нашло сегодня практическое применение в следующих областях:

архитектура (при строительстве Парфенона и собора Парижской Богоматери);

живопись (в картинах Леонардо да Винчи, Микеланджело, Шишкина);

музыка (в октавах Моцарта, Бетховена, Шопена).

Ученые до сих пор изучают число Фибоначчи, признавая, что это не до конца исследованное понятие.

Источник

Фибоначчи повсюду!

Числа Фибоначчи названы в честь Леонардо Фибоначчи из города Пизы (современная Италия). На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.

Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.

Числа Фибоначчи и золотое сечение

Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:

Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».

Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.

Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.

Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.

Почему эта последовательность настолько уникальна

Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.

Числа Фибоначчи в природе

Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.

Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.

Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.

Числа Фибоначчи в теле человека

Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.

Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.

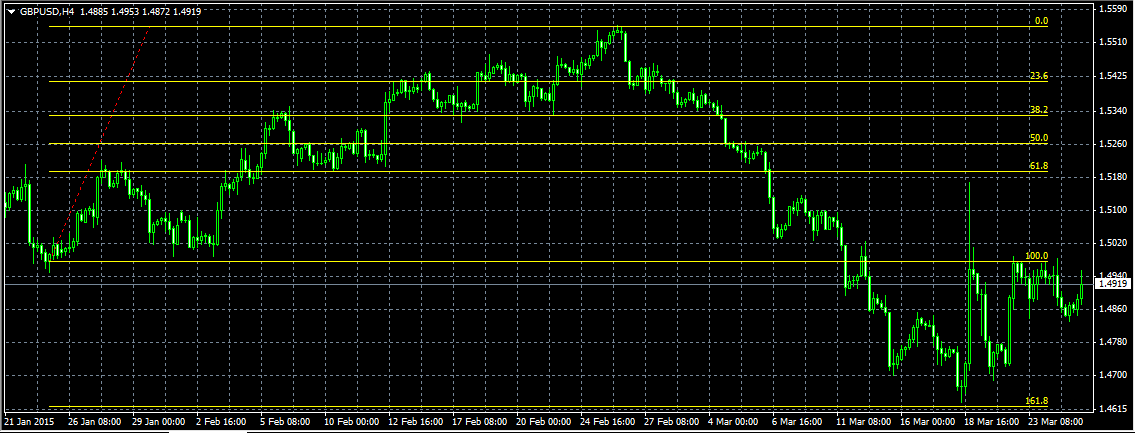
Числа Фибоначчи в биржевой торговле

Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.

Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2% (соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.

Числа Фибоначчи в фотографии и искусстве

В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.

Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.

Может именно из-за этого Дональд Трамп был избран президентом? (шутка):

Тем не менее, никогда не стоит недооценивать скрытые силы последовательности Фибоначчи.

Источник

Золотое сечение и числа Фибоначчи

Человек стремится к знаниям, пытается изучить мир, который его окружает. В процессе наблюдений появляются многочисленные вопросы, на которые, соответственно, требуется найти ответы. Человек ищет эти ответы, а находя их, появляются другие вопросы.

Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.

Леонардо был рожден в Пизе. Впоследствии получил прозвище Фибоначчи, что означает «хорошо рожденный сын». Когда Леонардо жил со своим отцом в странах Северной Африки, он изучал математику с арабскими учителями. Получив весь необходимый материал, он создал собственную книгу – «Книгу абака». Именно этот человек становится первым средневековым учёным, познакомившим Европу с арабской системой счисления, которой мы пользуемся всю нашу жизнь[1].

Основная задача, поясняющая возникновение ряда чисел Фибоначчи – задача о кроликах. Вопрос задачи звучит так: «Сколько пар кроликов в один год рождается от одной пары?». К задаче дано пояснение, что пара через месяц рождает ещё одну пару, а по природе кролики начинают объектом рождать потомство на второй месяц после своего рождения. Автор даёт нам решение задачи. Получается, что в первый месяц первая пара родит ещё одну. Во второй месяц первая пара родит ещё одну – будет три пары. В третий месяц родят две пары — изначально данная и рождённая в первый месяц. Получается пять пар. И так далее. Используя такую же логику в рассуждении, мы получим, что в четвёртый месяц будет 8 пар, в пятый– 13, в шестой – 21, в седьмой 34, в восьмой — 55, в девятый — 89, в десятый 144, в одиннадцатый – 233, в двенадцатый — 377[2](рис. 1).

Из этой задачи и можно вывести саму последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… В основе этой последовательности лежит алгоритм: начиная с «1, 1» следующим числом будет сумма двух предыдущих чисел. Разделив любой член данной последовательности на член, который стоит перед ним, мы получим величину, называемую «пропорцией Золотого сечения» — примерно 1, 618[3].

В эпоху Возрождения художники открыли некие зрительные центры, которые, влияя на психику человека, невольно приковывают наше внимание. Данные точки не зависят от формата картины. Их всего четыре, они делят картину в пропорциях Золотого сечения- примерно 3/8 и 5/8 (рис.2).

Для того чтобы привлечь внимание зрителя к определенному элементу картины, необходимо совместить его с одним из зрительных центров. Данное открытие назвали «золотое сечение картины»[4].

Правило золотого сечения используется в стоматологии, именно они используются при художественной реставрации зубов, их восстановлении. Рассмотрим эстетическое восстановление передних зубов, фронтального зубного ряда (рис. 3)[5].

Золотые пропорции включают в себя такие моменты:

— как ширина верхнего переднего зуба относится к ширине нижнего;

— как соотносятся между собой по ширине:

2 резца в нижнем фронтальном ряду;

двое резцов в верхнем ряду;

— какое имеется расстояние между премолярами и т.д.

Так же правило золотого сечения используется в косметологии и пластической хирургии. У людей с красивыми лицами существует идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это явление называется «динамической симметрией» или «динамическим равновесием».

Расстояние от линии смыкания губ до крыльев носа пропорционально расстоянию от линии губ до низшей точки подбородка в соотношении 1: 1,618. Ещё существует множество соотношений на лице, которые представлены на рисунке 4[6].

Числа Фибоначчи и Золотое сечение чтобы также используется и в психологии. Например, чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека. Если развернуть в ряд числа Фибоначчи, то получим: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т.д. Отношение между числами Фибоначчи составляет 0,618. Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества [7].

Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:

• 0 —начало отсчета — ребёнок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;

• 1 — ребенок овладел ходьбой и осваивает ближайшее окружение;

• 2 — понимает речь и действует, пользуясь словесными указаниями;

• 3 — действует посредством слова, задаёт вопросы;

• 5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребёнку охватить мир во всей его целостности;

• 8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии…

Закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.

В заключении отмечу, что данная работа является законченным исследованием и при этом имеет ряд перспектив. В дальнейшем возможно исследовать как числа Фибоначчи используются в биологии, химии, как это можно использовать и применять на практике в бытовых условиях.

1. Воробьев Н.Н. Числа Фибоначчи. – 5-е изд. – М.: Наука, 1978 – 144с.

Источник

masterok

Мастерок.жж.рф

Хочу все знать

Итак, мы выяснили с вами Кто такой Фибоначчи, а теперь давайте рассмотрим вот такой феномен.

Оказывается Фибоначчи повсюду!

На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.

Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.

Фибоначчи рассматривает гипотетическую ситуацию, когда в поле появляется пара кроликов. Они спариваются в конце месяца и в конце второго месяца самка производит еще одну пару. Кролики никогда не умирают, спариваются ровно через месяц, и самки всегда производят пару (один самец, одна самка). Вопрос, который поставил Фибоначчи был следующим: сколько пар будет через один год? Если посчитать, то окажется, что количество пар в конце N-го месяца равно Fn или N-му числу Фибоначчи. Таким образом, количество пар кроликов через 12 месяцев будет F12 или 144.

Числа Фибоначчи и золотое сечение

Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».

Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.

Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.

Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.

Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.

Почему эта последовательность настолько уникальна
Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.

Числа Фибоначчи в природе

Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.

Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.

Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.

Числа Фибоначчи в теле человека

Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.

Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.

Числа Фибоначчи в биржевой торговле

Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.

Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2% (соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.

Числа Фибоначчи в фотографии и искусстве

В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.

Сетка фи (красные линии) и спираль Фиббоначи в кадре.

Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.

Может именно из-за этого Дональд Трамп был избран президентом? (шутка):

И еще немного фундаментального числа!

Источник