что такое результирующий момент
Чему равен результирующий момент сил, действующих на тело?
Чему будет равна суммарная работа всех сил, действующих на локомотив, за первые 10 секунд от начала движения
Если локомотив массой 20 тонн начинает двигаться со станции так, что его скорость в зависимости от.
Найти работу, которую совершает над телом результирующий момент внешних сил
Шар массой 300 г и радиусом 4 см начинает вращаться относительно оси, проходящей через центр масс.
Найти: модуль суммарного момента сил, действующих на маховик; момент инерции маховика; его угловое ускорение
К ободу маховика в виде диска массой 20 кг и радиусом 10 см приложена сила 20 Н, направленная по.
Чему равен момент инерции полого цилиндра?
Чему равен момент инерции полого цилиндра относительно осей, x, y, z? Чему равен момент инерции.
Решение
Я теперь стал плохо соображать, поэтому проверьте, пожалуйста, мой расчёт.

Квадратный контур, сделанный из проводника длиной 2 м, расположенный в магнитном поле индукцией 1.
Чему равен момент, возникаемый в первом стержне. Задача по термеху
Всем привет. Есть стержень закрепленный на шарнире одник концом. Масса стержня сосредоточена в.
Чему равен и как направлен момент силы, действующей на диск
горизонтальный диск массой m и радиусом r вращается вокруг оси,проходящей через.
Контур имеет форму равностороннего треугольника со стороной b чему равен его магнитный момент
контур имеет форму равностороннего треугольника со стороной b чему равен его магнитный момент если.
Расчёт сил, действующих на конструкцию
Здравствуйте. Есть вот такая задачка: Есть конструкция: груз подвешен на балке разделённой на.
Нарисовать схему сил, действующих на рамку
Квадратная проволочная рамка со стороной а расположена в одной плоскости с длинным прямым проводом.
Большая Энциклопедия Нефти и Газа
Результирующие моменты сил в обеих частях компрессора расположены в плоскостях, вращающихся в направлении, обратном вращению вала, с той же частотой. Геометрическая сумма обоих результирующих моментов также является моментом, действующим во вращающейся плоскости. [1]
Результирующий момент силы вызывает прецессию пули, аналогичную прецессии волчка. Когда же пуля поворачивается немного боком ( вправо или влево), она отклоняется от намеченной траектории. [2]
Результирующий момент силы равен сумме составляющих моментов сил. [3]
Определение результирующего момента сил взаимодействия лопастного колеса с потоком жидкости представляет собой одну из основных задач гидродинамики лопастных машин. Основное уравнение лопастных гидромашин как для установившегося ( статического), так и для неустановившегося ( динамического) режима работы получают из теоремы о моменте количества движения, предполагая одномерный и осесимметричный поток в лопастном колесе. В соответствии с этой теоремой производная по времени от момента количества движения системы материальных точек относительно какой-либо оси равна сумме моментов всех внешних сил, действующих на систему. [4]
Определение результирующего момента сил взаимодействия лопастного колеса с потоком жидкости представляет собой задачу гидродинамики. [5]
Для вычисления результирующего момента сил сопротивления вращению шара в вязкой жидкости необходимо выражение (8.11) для ( pvs) a, умножить на элемент поверхности a2 sin bdbd. [6]
Для определения результирующего момента сил взаимодействия лопастей рабочего колеса с потоком жидкости необходимо знать действительное поле скоростей в межлопастных каналах, что представляет собой практически неразрешимую задачу. [7]
Обратно, если результирующий момент сил F относительно точки О равен нулю, то эти силы приводятся к одной результирующей, приложенной в этой точке. В этом случае равновесие должно иметь место, так как эта результирующая необходимо уравновешивается сопротивлением в точке О, которая закреплена неподвижно. В закрепленной точке развивается, таким образом, реакция связи R, равная и прямо противоположная геометрической сумме прямо приложенных сил. Реакция определяется, таким образом, вполне. [8]
Таким образом, результирующий момент сил воздействия вязкой несжимаемой жидкости на круглый цилиндр зависит только от коэффициента того слагаемого в ряде Лорана (5.17), которое содержит комплексное переменное л в первой степени. [9]
Показать, что в нашей системе отсчета результирующий момент сил Эйнштейна обращается в нуль. [11]
Для сохранения момента твердого тела требуется только, чтобы результирующий момент сил был равен нулю. [12]
Трение скольжения ( результирующая сила) и трение верчения ( результирующий момент сил ) при этом оказываются связанными между собою и, следовательно, изменение вертикальной составляющей угловой скорости шара влияет вообще на вид траектории движения центра шара. Вместе с тем при стремлении площадки контакта к нулю предельные движения шара переходят в движение шара с точечным контактом и, следовательно, идеализация соприкосновения поверхностей точечным контактом является правомерной. [14]
Савельев И.В. Курс общей физики, том I

Загрузить всю книгу 
Титульный лист
Главная редакция физико-математической литературы
Механика, колебания и волны,
КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I
Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.
Предисловие к четвертому изданию
При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.
Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.
Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.
Ноябрь 1969 г. И. Савельев
Из предисловия к четвертому изданию
Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.
При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.
Что такое результирующий момент
При поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, поэтому скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Поэтому достаточно определить движение одной из точек тела (например, его центра инерции) для того, чтобы полностью охарактеризовать его движение.
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.
причем для всех точек тела одно и то же. Разделив на соответствующий промежуток времени dt, получим скорость точки:
Следовательно, скорость этой точки при сложном движении тела имеет значение:
1.5.2. Движение центра инерции
(центра масс) твердого тела
Разбив тело на элементарные массы Δmi, можно представить его как систему МТ, взаимное расположение которых остается неизменным. Любая из этих элементарных масс может находиться под воздействием внутренних и внешних сил. Напишем для каждой элементарной массы уравнение второго закона Ньютона:
Однако сумма всех внутренних сил, действующих в системе, равна нулю. Поэтому (1.5.5) можно упростить так:
Используя определение центра инерции, можно записать:
Дифференцируя (1.5.7) дважды по времени, можно получить:
Подставляя (1.5.8) в (1.5.6), имеем:
Следовательно, центр инерции твердого тела движется так, как двигалась бы МТ с массой, равной массе тела, под действием всех приложенных к телу сил.
1.5.3. Момент силы
Рассмотрим схему установки на Рис. 1.5.1.
Рис. 1.5.1. Схема установки для исследования
равно-ускоренного вращательного движения
Под действием груза Р крестовина будет вращаться с возрастающей угловой скоростью, и вращение будет равно-ускоренным. Варьируя величину груза Р, радиус шкива l, массу грузов m и их расстояние R от оси вращения, можно прийти к заключению, что угловое ускорение β:
Следовательно, ускорение вращательного движения зависит не только от величины действующей на тело силы, но и от расстояния l от оси вращения до линии, вдоль которой действует сила. Произведение fl дает величину так называемого момента силы относительно оси вращения.
Из этого опыта следует также, что на величину углового ускорения влияет не только масса вращающегося тела, но и распределение массы относительно оси вращения. Величина, которая это учитывает, называется моментом инерции тела относительно оси вращения.
Рис. 1.5.2. К определению момента силы
Рис. 1.5.3. Момент пары сил
Полученное выражение не зависит от положения точки О на плоскости, в которой лежит пара сил.
Суммарный момент внутренних сил Силы, с которыми взаимодействуют друг с другом две любые элементарные массы, лежат на одной и той же прямой (Рис. 1.5.4).
Рис. 1.5.4. Момент внутренних сил
Их моменты относительно произвольной точки О равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы МТ, в частности, для твердого тела, всегда равна нулю.
1.5.4. Момент импульса материальной точки.
Закон сохранения момента импульса
Аналогично моменту силы введем момент импульса МТ относительно некоторой точки О:
Рис. 1.5.5. К определению момента импульса
Введя плечо l = rsinα, можно получить модуль вектора момента импульса в виде:
Продифференцируем (1.5.16) по времени:
1.5.5. Уравнение динамики
вращательного движения
Если МТ вращается по окружности радиуса r (Рис.1.5.6), то момент ее импульса относительно оси вращения О равен:
Рис. 1.5.6. К выводу уравнения динамики вращательного двмжения
Если вокруг оси О вращается система МТ с одной и той же угловой скоростью ω, то:
где, момент инерции системы МТ относительно оси вращения, равный сумме произведений масс МТ на квадраты их расстояний до оси вращения.
Важным частным случаем является вращение неизменяемой системы МТ или твердого тела вокруг неподвижной оси. В этом случае момент инерции I остается постоянным при вращении, и уравнение (1.5.22) будет иметь вид:
| — сила | — момент силы |
| — масса | — момент инерции |
| — линейная скорость | — угловая скорость |
| — линейная скорость | — угловая скорость |
| — линейное ускорение | — угловое ускорение |
| — импульс | — момент импульса |
Предположим, что твердое тело может изменять свою конфигурацию в результате перераспределения масс. Пусть в результате происходит изменение момента инерции от значения I1 до I2. Если такое перераспределение осуществляется при отсутствии моментов внешних сил, то согласно закону сохранения момента импульса должно выполняться равенство:
1.5.6. Момент инерции. Теорема Штайнера
Из определения момента инерции:
Распределение массы в пределах тела можно охарактеризовать с помощью физической величины, называемой плотностью. Если тело однородно, то его плотность может быть вычислена так:
Уменьшение объема в (1.5.27) следует производить до тех пор, пока не будет получен физически бесконечно малый объем, который достаточно мал, чтобы в его пределах макроскопические свойства вещества можно было считать одинаковыми, и достаточно велик, чтобы не могла проявиться дискретность (атомарное строение) вещества.
Согласно (1.5.27), элементарная масса тела может быть вычислена так:
Следовательно, момент инерции следует записать в виде:
Если плотность постоянна, ее можно вынести за знак суммы:
Устремляя ΔVi к нулю, можно в (1.5.30) перейти к интегрированию:
В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (Рис. 1.5.7).
Рис. 1.5.7. К расчету момента инерции диска
Разобьем диск на кольцевые слои толщиной dr. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном r. Объем такого слоя равен:
В данном случае вычисление момента инерции упрощалось благодаря однородности и симметричности тела. Если бы нужно было отыскать момент инерции относительно оси О’О’ (Рис. 1.5.7), перпендикулярной к диску и проходящей через его край, вычисления оказались бы значительно сложнее. В таких случаях отыскание момента инерции облегчается, если воспользоваться теоремой Штайнера : момент инерции I относительно произвольной оси равен сумме момента инерции I C относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
В соответствии с теоремой Штайнера момент инерции диска относительно оси О’О’ равен:
1.5.7. Работа и кинетическая энергия
вращающегося твердого тела
Если МТ вращается по окружности с радиусом r, то элементарная работа при повороте на угол dφ равна:
Кинетическая энергия твердого тела, вращающегося с угловой скоростью ω, может быть записана так:
Это выражение напоминает соответствующую формулу для кинетической энергии МТ и может быть получено из нее формальной заменой m → I, v → ω.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2013
СОДЕРЖАНИЕ
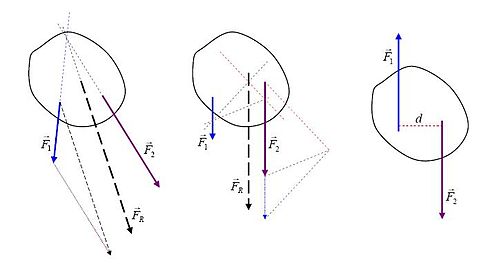
Иллюстрация
Схема иллюстрирует простые графические методы поиска линии приложения равнодействующей силы простых плоских систем.
Связанный вектор
Силы, приложенные к одной и той же точке, можно сложить, чтобы получить такое же воздействие на тело. Однако силы с разными точками приложения нельзя складывать вместе и поддерживать одинаковое воздействие на тело.
Изменить точку приложения силы просто, введя равные и противоположные силы в двух разных точках приложения, которые создают чистый крутящий момент на теле. Таким образом, все силы, действующие на тело, могут быть перемещены в одну точку приложения с соответствующими крутящими моментами.
Система сил на твердом теле объединяется путем перемещения сил в одну и ту же точку приложения и вычисления соответствующих крутящих моментов. Сумма этих сил и моментов дает результирующую силу-вращающий момент.
Соответствующий крутящий момент
Если точка R выбрана как точка приложения результирующей силы F системы из n сил F i, то соответствующий крутящий момент T определяется по формулам
таким образом, значение соответствующего крутящего момента остается неизменным.
Результат без крутящего момента
Если это условие выполнено, то есть точка приложения для результирующей, которая приводит к чистой силе. Если это условие не выполняется, то система сил включает чистый крутящий момент для каждой точки приложения.