что такое рекурсия php
Рекурсивные алгоритмы на PHP. Часть 1. Основы рекурсии
В этой статье я расскажу о рекурсии и о том как грамотно работать с ней на языке PHP.
PHP расшифровывается как PHP: Hypertext Preprocessor. Это смущает многих людей, потому что первое слово аббревиатуры это аббревиатура. Этот тип аббревиатуры называется рекурсивной аббревиатурой.
Перевод Google из официальной документации по PHP
Понятие рекурсии
Для начала разберёмся с понятием рекурсии. В общем смысле рекурсия это отображение чего-либо внутри самого себя. Рекурсивные алгоритмы используют рекурсивные функции, обладающие данным свойством.
Существует два варианта реализации рекурсивных функций: простой и сложный. В простом случае рекурсивная функция вызывает саму себя. В сложном — функция вызывает другую функцию, которая вызывает исходную функцию, с которой всё начиналось.
Рассмотрим пример из жизни. Если взять два больших зеркала и поставить их друг напротив друга, то можно увидеть бесконечный коридор из изображений зеркал. Каждое зеркало несёт в себе функцию отражения пространства расположенного перед ним. Поэтому здесь мы имеем пример сложной рекурсии (функция вызывает другую функцию, которая вызывает исходную).
Другим примером можно взять всем хорошо известное детское стихотворение:
Эта докучная сказка представляет собой пример простой рекурсии (здесь функция вызывает саму себя).
Глубина рекурсии
В связи с понятием рекурсии возникает понятие глубины рекурсии, то есть степени вложенности её отображений. Русская матрёшка, как правило, имеет 3-х и более вложенных в неё матрёшек. То есть глубина рекурсии в данном случае равна количеству вложенных матрёшек. Глубина рекурсии может быть равна бесконечности, в этом случае говорят о бесконечной рекурсии.
Два примера выше иллюстрируют именно этот случай. Правда в реальном мире, в отличие от мира математических абстракций, всегда есть какие-либо ограничения. Нельзя например бесконечно пересказывать одно и то же стихотворение, так как мы ограничены во времени.
Для нас важно, что ограничениям подвержен и сам компьютер. Память компьютера, производительность — не бесконечны. Поэтому применяя рекурсию, нужно понимать её опасности и подводные камни.
Применение простых алгоритмов в PHP: рекурсивный метод
Однажды я обнаружил очень интересную особенность развития современных web-программистов. Мы смело оперируем фабриками, синглтонами и декораторами, но забываем о такой фундаментальной части программирования, как классические алгоритмы. Ведь если присмотреться к их реализации, то это тоже своего рода паттерны. С институтской скамьи можно вспомнить, к примеру, nested sets, b-tree, сортировку «пузырьком». Реализация многих алгоритмов давно устоялась. А потому я хотел бы посвятить свою статью алгоритмам и их применении в PHP.
Начну я с самого простого — построения древовидной иерархии.
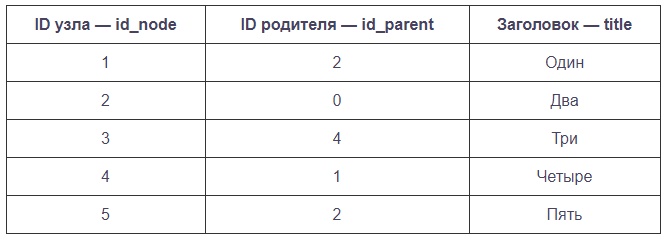
Казалось бы, что тут сложного? В базе данных есть таблица примерно следующего содержания:
Необходимо представить этот массив в виде древовидного меню. Я не буду говорить о том, какими неправильными способами можно решить эту задачу. Единственно верный подход в данном случае — рекурсивный метод.
Алгоритм (паттерн, если так хотите) будет примерно следующим: 0. Создаём объект дерева и выбираем все элементы в таблице. 1. Вызываем метод построения. Он инициализирует сборку массива родительских категорий. Именно этот момент является ноу-хау данного алгоритма. Он позволяет нам организовать изящную рекурсию. 2. Итеративно обходим массив, начиная с нулевого элемента. Выводим информацию о текущем элементе. 3. Увеличиваем уровень погружения. Рекурсивно вызываем метод для дочернего элемента. Если он есть в массиве родительских категорий, то идем к шагу 2, иначе — выходим в шаг-инициализатор. 4. Уменьшаем уровень погружения. Выходим из итерации.
Итак, метод сборки массива категорий будет выглядеть примерно вот так:
Далее напишем наш рекурсивный метод в соответствии с приведенным выше алгоритмом:
Теперь можем вызвать построение дерева, начиная с 0 элемента и 0 уровня. Замечу, что приведённый метод может вызывать построение с любой вложенной ноды и не ограничен по глубине.
А вот как будет выглядеть наше дерево в итоге:
Данный метод применим при построении меню на сайте, каталогов продукции и т. п. У него, разумеется, есть недостатки. При построении достаточно большого каталога метод будет работать довольно долго. Но выигрыш тут в том, что метод можно модифицировать и ограничить не только уровнем входа, но и уровнем погружения. Таким образом, можно достраивать дерево постепенно при запросе пользователей, что решит данную проблему.
Я не рассматриваю здесь проблемы хранения такой структуры, т. к. нас сейчас интересует только обход массива.
Рекурсия на PHP — алгоритм, применение
К написанию статьи сподвигли часы раздумий и экспериментов в области построения иерархических списков. Изначально логика обкатывалась на SQL запросах, но в последствии решил реализовать на PHP, дабы снять зависимость от СУБД. На простом примере я покажу как можно пройти от корня иерархии до каждого конечного элемента и обратно, информация скорее для новичков.
Итак, тестовая иерархия, с которой нам предстоит работать:
В базе данных имеется самая простая таблица на самом простом MSSQL сервере, тонкости подключения опустим, наша цель — разобраться с иерархией и рекурсией.
Описание полей есть в комментариях, чуть подробнее о поле access:
По умолчанию в моей системе для каждого нового документа проставляется inherit, то есть наследование от родителя. Для нашего эксперимента для некоторых эелементов пропишем доменные группы. В группе Domain Users моя учётная запись имеется, а вот в AD Group Secret меня нет.
Теперь предлагаю получить необходимые данные и перейти непосредственно к делу:
Задача №1
Необходимо научиться работать с иерархией как с деревом а не списком. Уровень вложенности заранее не известен и может быть любым, следовательно должно быть универсальное средство, позволяющее выполнять проход по дереву как сверху вниз, так и в обратном направлении.
Задача №2
Необходимо гибко управлять доступами, то есть, давать права на группы, отдельные документы и т.д., по аналогии с файловой системой NTFS, можно закрыть права на всю папку, но для одного документа в этой папке доступ нарезать — тоже самое должно получиться и у нас.
Задача №3
Необходимо скрыть от пользователей ресурсы, к которым у них нет доступа, но самое главное, при наличии прав хотя бы на один документ где то в глубине закрытой для него ветки, делать видимыми элементы ведущие к этому документу (иначе как пользователь до него доберётся?)
Вот собственно базовая функция:
Описание по большей части привёл в комментариях, но если говорить просто — после того как цикл foreach проходит строку и делает что то с данными(в нашем случае просто копирует данные в другой массив, добавляя поле level и точки к имени), он запускает эту же функцию, передав ей uid строки, и поскольку в условии if мы сравниваем его с pid, то следующий запуск однозначно захватит дочерние элементы. Цикл foreach перебирает все строки у которых uid родителя совпадает с переданным значением, поэтому перезапуская саму себя, функция отработает на каждом элементе каждого уровня. Для наглядности, мы так же передаём level увеличивая его на единицу. В итоге мы увидим какой документ какой уровень вложенности имеет.
Выводим массив $array в браузер:
Уже не плохо, не так ли?
А теперь немного усложним нашу функцию:
Разбираем по порядку:
1. Добавлено поле path — для формирования пути, добавляем к значению «/» и имя строки, затем полученное значение передаём в функцию, где история повторяется и на выходе получается путь от корня до элемента.
3. Добавлен индекс $array_idx_lvl = array();. Этот индекс нам так же потребуется позже, смысл таков — результирующий набор складывается не в одну кучу, а с разбивкой на массивы индексируемые по level.
4. Поле Access. Когда функция запускает саму себя, вместе с остальными параметрами она передаёт свою настройку прав $_row[‘access’] дочерям, а далее происходит следующее, проверяются права — если выставлено наследование (inherit), то применяются права родителя, если нет — через in_array проверяем, есть ли указанная в access доменная группа среди групп зашедшего пользователя. Если есть — добавляем в строку allow (разрешить), иначе deny (запрет).
Итоговый результат:
Ну что же, со спуском разобрались, теперь осталось разобраться с подъёмом и заполнением последнего поля view, определяющего видимость элементов. В начале статьи, я говорил для чего это нужно, но можно предположить иную ситуацию. Допустим вы решили привязать древовидный список к навигационному меню сайта, сделанному в виде многоуровневого выпадающего списка с кучей пунктов, и вы просто не хотите, чтобы пользователь, имеющий доступ всего лишь к одному документу ворочал весь этот массив и в объёмном меню искал свой пункт, ведь по сути ему нужно показать всего лишь одну ветку ведущую к нужной кнопке.
Почему здесь нужен проход в обратную сторону? Предположим у пользователя закрыт доступ для всего контента за исключением одного, самого дальнего(на последнем уровне) документа, если подумать, логично было бы брать начало от доступного, и вести его к корню дерева, показывая только нужные элементы.
Что делает эта функция — принимает в качестве параметра uid строки, с которой нужно начать действовать, обращается к этой строке и проверяет видимость. Если в поле view не show(т.е. показывать), а что то другое, проверяет что находится в безопасности, и если там стоит allow(доступ открыт), делает элемент видимым, в противном случае скрытым(hide), затем запускает себя же, передавая свой pid и настройку видимости, а так же переменную $ident увеличенную на 1, тем самым блокируя последующие самозапуски. При втором проходе, по переданному pid находится родительский элемент, выполняется та же проверка, за исключением одного, если от дочернего в переменной $view передано ‘show‘, то не смотря ни на что, текущему элементу так же присвоится show, то есть видимый.
На мой взгляд, работа с ограничителем — самый оптимальный вариант, ибо представьте ситуацию, на 10 уровне у нас 100 документов, для полного обхода всего дерева, нам нужно запускать эту функцию на каждом элементе, т.к. если на последнем уровне мы запустим функцию 100 раз, то выполняя самозапуски, перебор 100 раз дойдёт до корня. Если умножить на 10 уровней — уже получится 1000 циклов, что не есть хорошо, поэтому подъём нужно осуществлять равномерно, уровень за уровнем.
Запускает эту функцию следующий код:
Вот тут как раз и потребовался индекс по уровню. Здесь мы движемся от самого дальнего уровня, заходя в каждый, обрабатывая в нём каждый элемент.
Перед запуском, я намеренно прописал разрешающую группу для пункта «Отчет для налоговой», чтобы наглядно показать что код отрабатывает корректно. Несмотря на то, что доступ к разделу «Бухгалтерская отчетность» закрыт, он видимый.
Вот и собственно всё, думаю с задачей мы справились, основа получена, алгоритм работает, можно применить в реальной системе.
Рекурсия на PHP
В этой статье расскажу вам о рекурсии и о том как грамотно работать с ней на языке PHP.
PHP расшифровывается как PHP: Hypertext Preprocessor. Это смущает многих людей, потому что первое слово аббревиатуры это аббревиатура. Этот тип аббревиатуры называется рекурсивной аббревиатурой.
Перевод Google из официальной документации по PHP
Понятие рекурсии
Для начала разберёмся с понятием рекурсии. В общем смысле рекурсия это отображение чего-либо внутри самого себя. Рекурсивные алгоритмы используют рекурсивные функции, обладающие данным свойством.
Существует два варианта реализации рекурсивных функций: простой и сложный. В простом случае рекурсивная функция вызывает саму себя. В сложном — функция вызывает другую функцию, которая вызывает исходную функцию, с которой всё начиналось.
Рассмотрим пример из жизни. Если взять два больших зеркала и поставить их друг напротив друга, то можно увидеть бесконечный коридор из изображений зеркал. Каждое зеркало несёт в себе функцию отражения пространства расположенного перед ним. Поэтому здесь мы имеем пример сложной рекурсии (функция вызывает другую функцию, которая вызывает исходную).
Другим примером можно взять всем хорошо известное детское стихотворение:
…
Эта докучная сказка представляет собой пример простой рекурсии (здесь функция вызывает саму себя).
Глубина рекурсии
В связи с понятием рекурсии возникает понятие глубины рекурсии, то есть степени вложенности её отображений. Русская матрёшка, как правило, имеет 3-х и более вложенных в неё матрёшек. То есть глубина рекурсии в данном случае равна количеству вложенных матрёшек. Глубина рекурсии может быть равна бесконечности, в этом случае говорят о бесконечной рекурсии.
Два примера выше иллюстрируют именно этот случай. Правда в реальном мире, в отличие от мира математических абстракций, всегда есть какие-либо ограничения. Нельзя например бесконечно пересказывать одно и то же стихотворение, так как мы ограничены во времени.
Для нас важно, что ограничениям подвержен и сам компьютер. Память компьютера, производительность — не бесконечны. Поэтому применяя рекурсию, нужно понимать её опасности и подводные камни.
Опасности и подводные камни рекурсии
Рассмотрим простой пример.
Здесь функция foo() должна вызывать самое себя до бесконечности. В реальных условиях запуск программы приведёт к Segmentation fault, так как произойдёт переполнение стека вызова в силу ограничений на выделенную под него память. Понимая это следует избегать таких конструкций при разработке.
То же самое касается и примера со сложной рекурсией.
В PHP две функции не могут вызывать друг друга бесконечно, так как это неизбежно
приведёт к падению программы.
Теперь вернёмся к понятию глубины рекурсии. И рассмотрим следующий пример.
Здесь рекурсивный вызов должен завершиться по достижении степени вложенности n.
На практике при запуске этой программы для больших значений n произойдёт та же самая ошибка переполнения стека. Это так же следует учитывать при обработке больших списков и других структур данных, в которых глубина рекурсии зависит от их размера.
Рекурсивные алгоритмы на PHP
Теперь мы можем приступить к исследованию алгоритмов основанных на рекурсии.
Существует множество таких алгоритмов:
Рассмотрим некоторые из них.
Вычисление последовательности Фибоначчи
Следует сделать лирическое отступление, которое касается истории открытия данной последовательности…
В 1202 году Леонардо Пизанский, известный как Фибоначчи, решая задачу о размножении кроликов, пришёл к открытию рекуррентного соотношения: 

Вернёмся к нашему алгоритму. Знание рекуррентного соотношения позволяет нам с лёгкостью реализовать этот алгоритм на PHP:
С точки зрения программирования нам интересно знать насколько быстро он выполняется по сравнению с его реализацией на основе итераций, например этой:
Дело в том, что реализация рекурсивного алгоритма “в лоб” обладает одним существенным недостатком. А именно при такой реализации вызов функции для одного и того же аргумента производится многократно. Чтобы это увидеть, нужно внимательно рассмотреть само рекуррентное соотношение.
Повторные вызовы функции с одинаковыми аргументами занимает дополнительное время. Чтобы избежать этого, используют подход восходящего динамического программирования, который состоит в том, что задача разбивается на подзадачи и каждая подзадача решается только один раз. В нашем примере это можно реализовать в виде :
Таким образом вызов функций над одним и тем же аргументом производится лишь однажды, в случае повторных вызовов производится обращение к памяти к уже вычисленным значениям. Такой алгоритм выполняется гораздо быстрее, чем его простая реализация. Но всё же при этом он значительно уступает итеративной версии. Вы спросите в чём же дело?
Оказывается, что при рекурсивном вызове функций создаются копии её аргументов в стеке и следовательно дополнительные затраты на время выполнения операций копирования.
Чтобы обойти это, может быть использована парадигма Объектно-Ориентированного Программирования (ООП). К примеру мы можем создать массив внутри объекта, который будет иметь рекурсивный метод, внутри которого будет доступ к этому массиву так, что не потребуется передавать этот массив в качестве параметра для каждого вызова этого метода:
Время выполнения этой программы уже приближается к времени выполнения программы основанной на итерациях. Но всё же для достаточно больших значений n мы будем иметь отставание рекурсивной версии от его итеративного эквивалента, которое может быть значительным в практическом плане. Тогда же в чём смысл рекурсии спросите вы?
Предлагаю вам пока самостоятельно поразмышлять на эту тему.
Рекурсия на PHP
В этой статье расскажу вам о рекурсии и о том как грамотно работать с ней на языке PHP.
PHP расшифровывается как PHP: Hypertext Preprocessor. Это смущает многих людей, потому что первое слово аббревиатуры это аббревиатура. Этот тип аббревиатуры называется рекурсивной аббревиатурой.
Перевод Google из официальной документации по PHP
Понятие рекурсии
Для начала разберёмся с понятием рекурсии. В общем смысле рекурсия это отображение чего-либо внутри самого себя. Рекурсивные алгоритмы используют рекурсивные функции, обладающие данным свойством.
Существует два варианта реализации рекурсивных функций: простой и сложный. В простом случае рекурсивная функция вызывает саму себя. В сложном — функция вызывает другую функцию, которая вызывает исходную функцию, с которой всё начиналось.
Рассмотрим пример из жизни. Если взять два больших зеркала и поставить их друг напротив друга, то можно увидеть бесконечный коридор из изображений зеркал. Каждое зеркало несёт в себе функцию отражения пространства расположенного перед ним. Поэтому здесь мы имеем пример сложной рекурсии (функция вызывает другую функцию, которая вызывает исходную).
Другим примером можно взять всем хорошо известное детское стихотворение:
…
Эта докучная сказка представляет собой пример простой рекурсии (здесь функция вызывает саму себя).
Глубина рекурсии
В связи с понятием рекурсии возникает понятие глубины рекурсии, то есть степени вложенности её отображений. Русская матрёшка, как правило, имеет 3-х и более вложенных в неё матрёшек. То есть глубина рекурсии в данном случае равна количеству вложенных матрёшек. Глубина рекурсии может быть равна бесконечности, в этом случае говорят о бесконечной рекурсии.
Два примера выше иллюстрируют именно этот случай. Правда в реальном мире, в отличие от мира математических абстракций, всегда есть какие-либо ограничения. Нельзя например бесконечно пересказывать одно и то же стихотворение, так как мы ограничены во времени.
Для нас важно, что ограничениям подвержен и сам компьютер. Память компьютера, производительность — не бесконечны. Поэтому применяя рекурсию, нужно понимать её опасности и подводные камни.
Опасности и подводные камни рекурсии
Рассмотрим простой пример.
Здесь функция foo() должна вызывать самое себя до бесконечности. В реальных условиях запуск программы приведёт к Segmentation fault, так как произойдёт переполнение стека вызова в силу ограничений на выделенную под него память. Понимая это следует избегать таких конструкций при разработке.
То же самое касается и примера со сложной рекурсией.
В PHP две функции не могут вызывать друг друга бесконечно, так как это неизбежно
приведёт к падению программы.
Теперь вернёмся к понятию глубины рекурсии. И рассмотрим следующий пример.
Здесь рекурсивный вызов должен завершиться по достижении степени вложенности n.
На практике при запуске этой программы для больших значений n произойдёт та же самая ошибка переполнения стека. Это так же следует учитывать при обработке больших списков и других структур данных, в которых глубина рекурсии зависит от их размера.
Рекурсивные алгоритмы на PHP
Теперь мы можем приступить к исследованию алгоритмов основанных на рекурсии.
Существует множество таких алгоритмов:
Рассмотрим некоторые из них.
Вычисление последовательности Фибоначчи
Следует сделать лирическое отступление, которое касается истории открытия данной последовательности…
В 1202 году Леонардо Пизанский, известный как Фибоначчи, решая задачу о размножении кроликов, пришёл к открытию рекуррентного соотношения: 

Вернёмся к нашему алгоритму. Знание рекуррентного соотношения позволяет нам с лёгкостью реализовать этот алгоритм на PHP:
С точки зрения программирования нам интересно знать насколько быстро он выполняется по сравнению с его реализацией на основе итераций, например этой:
Если сделать тест выполнения с замером времени с помощью функции microtime, то обнаружится, что итеративная версия алгоритма выполняется гораздо быстрее, нежели его рекурсивный аналог. Почему это происходит?
Дело в том, что реализация рекурсивного алгоритма “в лоб” обладает одним существенным недостатком. А именно при такой реализации вызов функции для одного и того же аргумента производится многократно. Чтобы это увидеть, нужно внимательно рассмотреть само рекуррентное соотношение.
Повторные вызовы функции с одинаковыми аргументами занимает дополнительное время. Чтобы избежать этого, используют подход восходящего динамического программирования, который состоит в том, что задача разбивается на подзадачи и каждая подзадача решается только один раз. В нашем примере это можно реализовать в виде :
Таким образом вызов функций над одним и тем же аргументом производится лишь однажды, в случае повторных вызовов производится обращение к памяти к уже вычисленным значениям. Такой алгоритм выполняется гораздо быстрее, чем его простая реализация. Но всё же при этом он значительно уступает итеративной версии. Вы спросите в чём же дело?
Оказывается, что при рекурсивном вызове функций создаются копии её аргументов в стеке и следовательно дополнительные затраты на время выполнения операций копирования.
Чтобы обойти это, может быть использована парадигма Объектно-Ориентированного Программирования (ООП). К примеру мы можем создать массив внутри объекта, который будет иметь рекурсивный метод, внутри которого будет доступ к этому массиву так, что не потребуется передавать этот массив в качестве параметра для каждого вызова этого метода:
Время выполнения этой программы уже приближается к времени выполнения программы основанной на итерациях. Но всё же для достаточно больших значений n мы будем иметь отставание рекурсивной версии от его итеративного эквивалента, которое может быть значительным в практическом плане. Тогда же в чём смысл рекурсии спросите вы?
Предлагаю вам пока самостоятельно поразмышлять на эту тему.