что такое редуцирование в геодезии
Редуцирование пунктов строительной сетки
Геодезическая строительная сетка
Геодезическая строительная сетка является одним из более национальных видов обоснования при строительстве промышленных и гражданских сооружений.
ГССН применяется в качестве
1. Планового и высотного обоснования, для выноса в натуру основных осей сооружения.
2. В качестве плановой и высотной основы исполнительных съемок, проводимых в ходе строительства и после его завершения.
3. Применяется для проектирования генерального плана промышленных и гражданских сооружений.
4. Применяется для решения задач горизонтальной и вертикальной планировки.
Геодезическая строительная сетка имеет преимущества перед другими видами планового обоснования, а именно:
1. При наличии строительной сетки разбивочные работы выполняются с одинаковой точностью на всей территории строительной площадки.
2. Значительно упрощается подготовка данных для разбивочных работ.
З. Упрощается процесс переноса проекта в натуру, так как можно применять простые методы (способ прямоугольных координат, линейные засечки).
4.В целях контроля любая точка сооружения может быть вынесена дважды от разных точек и сторон.
5. Пункты строительной сетки можно использовать для других геодезических работ, например, исполнительных съёмок.
Формы и размеры
Геодезическая сетка представляет собой систему квадратов или прямоугольников покрывающих строительную площадку, в вершинах которых расположены опорные пункты. Направление осей выбирают параллельно основным осям инженерных сооружений. Длину струны квадрата принимают от 100 до 500 метров. В зависимости от типа строящегося объекта и назначения. Наибольшее распространение получила сетка с длиной стороны 200х200 метров. Для установки технологического оборудования применяют сетку с 10-20 метров.
Система координат ГССН.
Редуцирование пунктов строительной сетки
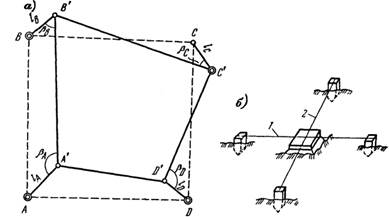
Детальную разбивку сетки, т.е. построение на местности сетки квадратов, можно выполнять различными способами. При большой площади строительной площадки применяют способ редуцирования, который обеспечивает высокую точность получения координат пунктов строительной сетки. Отисходных направлений разбивают сетку квадратов с точностью 1:2000 и закрепляют их вершины временными знаками. По этим пунктам прокладывают полигонометрические ходы, уравнивают их и получают исполнительные координаты. Сравнивая их значения с проектными, находят величины редукций (поправок), на которые перемещают каждый пункт сетки. Редуцирование выполняется с точностью ± 3 мм. После редуцирования пункты геодезической строительной сетки закрепляют постоянными знаками и выполняют контрольные измерения. Если ошибок не обнаружено, то координаты пунктов строительной сетки принимают равными проектным.
А) Схема редуцирования пунктов строительной сетки
Б) закрепление пункта постоянным знаком
1. Одной из вершин, присваивается условные координаты, остальные должны быть положительными или кратные 100 м. рекомендуется ЮЗ углу придать начальные координаты 0.0 и считать его за начальный пункт сетки. Координатные оси обозначать буквами (Х/А- ось абсцисс, У/В- ординат).
2. Направление А и В совместить с основными осями сооружения.
3. Пунктам сетки присвоить порядковую нумерацию. Для обозначения № пункта к буквам А и В добавить индекс указывающий число сотен метров по оси Х и У (4А/6В). Будет указывать координаты Х-400, У-600.
Что такое редуцирование в геодезии
Автор статьи: А. М. Ицков, геодезист. г. Иркутск
Ввод поправок за редукции линий на эллипсоид и плоскость – один из способов повышения точности съемочного обоснования
Как известно, при вычислении координат съемочного обоснования, в измеренные величины не вводятся поправки за редукцию с поверхности Земли на поверхность референц-эллипсоида и за редуцирование с эллипсоида на плоскость (далее – редукции и поправки за редукции). До появления компьютеров, ввод поправок за редукции занимал бы слишком много времени. Поэтому действующие инструкции (порядком устаревшие), не требуют ввода поправок за редукцию. В настоящее время расчеты, как правило, производятся при помощи специальных программ и учет редукций не усложняет камеральные работы. Однако считается, что в вводе поправок за редукции нет необходимости вследствие того, что они малы. Так ли это?
Рассмотрим этот вопрос.
В данной статье мы рассмотрим системы координат, параметры которых известны.
В России, в качестве государственной, принята система координат 95 года (СК-95г). В ней принят эллипсоид Красовского и проекция Гаусса-Крюгера. Данная проекция является частным случаем Поперечно-цилиндрической проекции Меркартора. Для обеспечения единой геодезической основы больших и протяженных объектов, например нефтепровод «Восточная Сибирь – Тихий океан», иногда применяется система координат 95 года.
Так же, для геодезической основы изысканий и строительства объектов, начали использовать систему координат WGS-84, UTM (Проект Сахалин-2, Береговые трубопроводы). В системе WGS-84, UTM принят эллипсоид WGS-84 и проекция Гаусса-Боага, так же являющаяся частным случаем поперечно-цилиндрической проекции Меркартора.
| Система координат | СК-95г | WGS-84, UTM |
| Проекция | (Гаусса-Крюгера) | (Гаусса-Боага) |
| Смещение на север No | 0 | 0 |
| Смещение на восток Eo | 500000 | 500000 |
| Масштаб по осевому мередиану ( mo ) | 1 | 0,9996 |
| Применяемый эллипсоид | Красовского | WGS-84 |
| Большая полуось эллипсоида, м | 6378245 | 6378137 |
| Сжатие эллипсоида | 1/298.3 | 1/298.257223563 |
Как мы видим, различие систем координат СК-95г и WGS-84, UTM состоит в несколько разных размерах большой полуоси исходных эллипсоидов и в довольно существенной разнице масштабов по осевому меридиану. Поскольку системы координат используют одну проекцию, то для съемочных сетей, формулы вычисления поправок за редукцию измеренных величин будут общими. Мы не будем приводить всех поправок, которые крайне малы и вводятся только при обработке высокоточных геодезических сетей. Рассмотрим только редукцию измеренных линий на эллипсоид и на плоскость.
Формулы вычисления редукций.
Редуцирование измеренных линий на поверхность референц- эллипсоида.
Для территории России принимаем среднее значение R=6380000 м [1]
Редуцирование линий на плоскость
Поскольку стороны в съемочном обосновании редко превышают 1000 м, то формулу 1 [1] можно записать в следующем виде:
На основании формул 1 и 2 получаем формулу суммарной поправки в линии:
В СК-95г и WGS-84, UTM для исключения отрицательных значений, ордината имеет смещение на +500000м. Формула (3) будет иметь вид:
Используя формулу ( 4 ) вычислим поправки за редукцию на эллипсоид и за редукцию на плоскость в системах координат СК-95г и WGS-84, UTM в линии длиной 1000 метров.
Таблица 2. Поправки в линию длиной 1000м в СК-95г и СК-63г.
Таблица 3. Поправки в линию длиной 1000м в СК WGS-84, UTM.
Как видно из таблиц, поправки могут быть как совсем небольшими, так и достигать значительных величин.
Возникает вопрос: «Всегда ли надо вводить поправки?»
В таблицах 2 и 3 желтым цветом выделены поправки менее 0.050 м на один километр. То есть, когда поправки можно не учитывать. Жирным курсивом выделены ошибки более среднеквадратической (более 0.25м на 1000м), когда поправки однозначно необходимо вводить в измеренные линии.
Система координат 95года. Ширина зоны в СК-95г равна 6 градусам. На территории России максимальное расстояние от осевого меридиана до края зоны составляет порядка 250 км. На краю зоны поправки за редуцирование могут достигать 0.76м на 1000м. Однако стоит отметить, что в диапазоне: высот от 0 до 500м и на расстоянии от осевого меридиана от 0 до 50км, редукции весьма малы. На каждом отдельном объекте геодезистам необходимо оценивать поправки за редукции и самостоятельно принимать решение о целесообразности их введения в измеренные линии.
Система координат 63г. Ширина зоны в СК-63г равна 3 градусам. Максимальное расстояние до края зоны в России составляет порядка 125 км. Обратимся к таблице 2. Учитывая, что в подавляющем большинстве случаев расстояние от осевого меридиана редко достигает 100км, можно сделать вывод о том, что в большинстве случаев поправки за редукцию измеренных линий будут небольшими. В том случае, если все необходимые параметры известны, то можно рассчитать и оценить величину поправки за редукцию.
Система координат WGS-84, UTM. Поправки значительные. Небольшие по своей величине поправки только при расстоянии 200км от осевого меридиана. При работе с системой координат WGS-84, UTM поправки за редуцирование линий необходимо вводить постоянно.
Уравнивание геодезических сетей по способу наименьших квадратов (МНК) производится при условии, что:
все измеренные в сети величины являются независимыми
в результатах измерений отсутствуют систематические ошибки
случайные ошибки измерений подчиняются закону нормального распределения
Погрешности, вызванные игнорированием редукций, аналогичны систематическим ошибкам. Корректное уравнивание сетей съемочного обоснования вследствии этого невозможно.
Тем не менее, считается, что поправки при уравнивании компенсируют поправки за редукции. Поэтому при создании планового обоснования нет необходимости в учете этих редукций. Рассмотрим этот вопрос на примере двух теодолитных ходов.
Воспользуемся программой CREDO DAT. Создадим проект теодолитного хода с нулевой невязкой, с учетом параметров СК-42г. Координаты возьмем в проекции Гаусса-Крюгера, ордината – 150 км, отметка 50м над уровнем моря. Суммарная поправка 0.269м на 1000 метров. Получим таким образом «истинные» координаты. После этого установим систему координат «Местная» и отключим учет поправок. Смоделируем уравнивание хода без ошибок в измерениях, но и без редукций. Сравним полученные результаты.
Таблица 4. Сравнение координат точек хода из двух вариантов уравнивания.
Таблица 5. Характеристики теодолитного хода.
Допустимая средняя ошибка определения координат точек хода составляет 0.1 мм в масштабе плана. В нашем случае – 0.10 м. Соответственно средняя квадратическая ошибка – 0.14 м и предельная ошибка – 0.28 м.
Полученная погрешность определения координат точек теодолитного хода в слабом месте практически равна предельной погрешности.
Таблица 6. Сравнение координат точек из двух вариантов уравнивания.
Таблица 7. Сравнение дирекционных углов сторон хода
Таблица 8. Характеристики теодолитного хода.
| рис. 3. Схема хода | Рис. 4. Журнал измерений хода |
Вследствии того, что ход с координатной привязкой, искажаются не только линии, но и азимуты сторон. В таблице 7 приведены дирекционные углы сторон хода. Искажения достигают 02’34». Так же показателен тот факт, что вычисленная фактическая угловая ошибка хода ( табл. 8 ) превышает допустимую погрешность.
В обоих примерах полученные погрешности определения координат точек планового обоснования, в слабом месте, сопоставимы с предельно допустимыми ошибками. В примере хода с координатной привязкой, ошибки дирекционного угла стороны достигли 02’34». Все эти ошибки обусловлены только неправильной математической обработкой. Если добавить ошибки измерений, то погрешности будут гораздо больше. Возможно, из-за этого появляется недоверие к уравниванию геодезических сетей в целом.
Рекомендации по обработке геодезических измерений.
1. При помощи программы CREDODAT.
Создание различных систем координат в проекте CREDO DAT 3.0 детально описано в главе 3 описаний к программе и в статье «Создание пользовательской системы координат в CREDO_DAT» [ 1 ]. Параметры проекций Гаусса-Крюгера и UTM приведены в таблице 1 данной статьи. Однако необходимо добавить, что для правильного редуцирования измеренных линий на эллипсоид, необходимо вводить отметки точек. При совместной обработке нивелирования и плановых сетей проблем не возникает. Если же уравнивается только плановое обоснование, то можно вводить отметки для каждой точки. Либо можно ввести среднюю отметку на объекте. При правильной настройке проекта все поправки вносятся в измеренные величины автоматически.
2. При помощи программы «TRIMBLE GEOMATIC OFFICE» (далее TGO).
3. Ввод поправок в измерения за редукции «вручную» при помощи таблиц.
Можно составить таблицы поправок для конкретного объекта, рассчитав поправки по формуле ( 3 ). Выбрать интервал значений Y (от 50км до 65 например) и среднюю отметку для объекта. По одной оси откладывать Y, по другой длины линий. Интервал линий рекомендуется брать через 10метров (210м, 220м, 230м и т.д.). Интервал значений Y через 10 км.
Способ редуцирования
При способе редуцирования сетку вначале выносят в натуру с точностью теодолитного хода и закрепляют временными знаками: деревянными столбами с гвоздем в торце, обозначающим центр; металлическими штырями или трубками на бетоне с накерненными центрами. Затем производят точные измерения, по результатам которых определяют фактическое положение временных пунктов. Из решения обратных задач между проектными и фактическими координатами пункта определяют данные для его смещения (редуцирования) в проектное положение. Найденную точку закрепляют постоянным знаком.
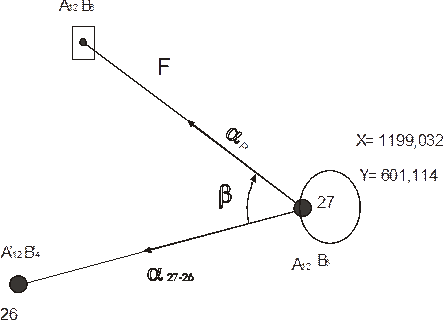
Рассмотрим технику редуцирования. Пусть пункту строительной сетки A12B6 соответствует временный пункт 27, для которого определены координаты х= 1199,032 и у=601,114 (рис. 40).
Рисунок 40 – Техника редуцирования
Дирекционный угол на смежный временный пункт 26- 270° 43’18». Из решения обратной задачи находим дирекционный угол редукции и ее линейный элемент:
¢19²;
м,
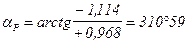
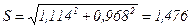
а затем угловой элемент редукции:
b=310 59’19»-270° 43’18» = 40° 16′ 01″.
Окончательное положение отредуцированной точки закрепляют на торце колышка гвоздиком. При отложении линейного элемента редукции, в случае необходимости, вводят поправку за наклон со знаком плюс по формуле:
,
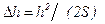
Если временный знак сдвинут незначительно или редуцирование выполняется непосредственно на головке знака, то, зафиксировав на горизонтальном круге теодолита направление с временного знака на постоянный, натягивают от центра временного знака в коллимационной плоскости теодолита струну или леску, фиксирующую это направление на местности, и вдоль нее откладывают линейный элемент редукции.
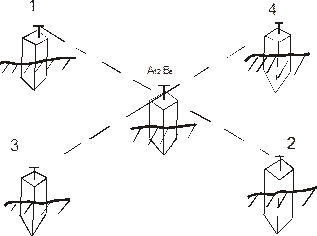
Рисунок 41 – Схема установки постоянных знаков
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Геодезия
Для студентов аспирантов и преподавателей
Разделы
Понятие о редукционной задаче
Под редукционной задачей высшей геодезии принято понимать комплекс проблем, связанных с разработкой математически строгого метода редуцирования измеренных величин с физической поверхности Земли на поверхность принятого референц-эллипсоида и необходимых для этого методов определения уклонений отвесных линий, а также геодезических высот пунктов над эллипсоидом.
В каждой стране принятый референц-эллипсоид должен быть ориентирован относительно оси вращения Земли и однозначно «закреплен» в теле Земли при помощи так называемых исходных геодезических дат, за которые принимают геодезические координаты Во, Lо, Но исходного пункта астрономо-геодезической сети. Исходные геодезические даты определяют, используя измерительную информацию всей астрономо-геодезической сети. Методы их определения рассматриваются в курсе теоретической геодезии.
Все измеренные в геодезической сети величины: горизонтальные направления, длины и азимуты сторон и т. п. редуцируют на поверхность референц-эллипсоида, применяя предложенный в 1934 г. Ф. Н. Красовским теоретически строгий метод проектирования. Проектирование измеренных величин осуществляется по нормалям к поверхности эллипсоида. Измеренные же величины (направления, азимуты и т. п.) связаны с отвесными линиями. Поэтому для редукции измеренных элементов на эллипсоид необходимо знать уклонения отвесных линий на пунктах геодезической сети, а также высоты пунктов над эллипсоидом. При решении редукционной задачи необходимо соблюдать следующие основные требования:
· редукционные поправки должны определяться с такой точностью, чтобы их ошибки были пренебрегаемо малы по сравнению с ошибками измерений редуцируемых величин. Другими словами, ошибки определения редукционных поправок и их влияние должны быть в пять—десять раз меньше ошибок самих измерений;
· формулы, используемые для вычисления редукционных поправок, должны быть получены с такой точностью, чтобы их погрешности не оказывали влияния на результаты вычисления редукций;
Уклонения отвесных линий при работах в горных районах должны быть известны для всех пунктов 1—3 классов. В астрономо-геодезической сети определяют астрономические широты и долготы l на отдельных пунктах в среднем через 70—100 км. Вычислив для этих пунктов геодезические широты В и долготы L, определяют по формулам (2.4) искомые уклонения отвесных линий. Для промежуточных пунктов их определяют путем косвенного интерполирования полученных уклонений с учетом нелинейности их изменений между пунктами. Для этого выполняют гравиметрическую съемку местности по определенной программе и для всех пунктов вычисляют сначала гравиметрические уклонения отвесных линий ξгр, hгр а затем с учетом их находят искомые уклонения ξar, har. Зная астрономо-геодезические уклонения отвесных линий ξar, harи расстояния между пунктами, определяют превышения квазигеоида и его высоты N над эллипсоидом (аномалии высот С). Определив в результате нивелирования нормальные высоты пунктов Ну, вычисляют их геодезические высоты по формуле (1.19).
Идея метода косвенного интерполирования астрономо-геодезических уклонений отвесных линий с использованием данных гравиметрической съемки и последующего вычисления превышений геоида предложена Ф. Н. Красовским в 1934 г. Этот метод был назван методом астрономо-гравиметрического нивелирования. Позднее он был развит в работах М. С. Молоденского применительно к предложенной им теории изучения фигуры и гравитационного поля Земли.
Астрономо-гравиметрический метод определения уклонений отвесных линий и превышений квазигеоида требует выполнения в большом объеме геодезических, астрономических и гравиметрических измерений. А следовательно, для его реализации необходимы и значительные затраты труда, средств и времени, которые особенно велики при работах в горах. В настоящее время в связи с бурным развитием науки и техники разрабатываются и постепенно внедряются высокоточные геодезические гравиинерциальные системы, позволяющие непосредственно, в кратчайшие сроки и с высокой точностью порядка 0,1″ измерять приращения астрономо-геодезических уклонений отвесных линий при переходе от одного пункта к другому, в том числе и в горных условиях. Измерив приращения астрономо-геодезических уклонений отвесных линий и зная расстояния между пунктами, можно вычислить превышения квазигеоида (геоида) между ними с достаточно высокой точностью. Данный метод изучения поверхности квазигеоида (геоида) целесообразно назвать методом гравиинерциального нивелирования. Этот метод может стать наиболее эффективным и точным методом изучения поверхности квазигеоида (геоида) особенно в континентальной части земного шара, где метод спутниковой альтиметрии не пригоден.
Определив на пунктах геодезической сети уклонения отвесных линий, а также геодезические высоты пунктов, вычисляют поправки в измеренные расстояния, горизонтальные направления, азимуты и т. п. за редукцию их к поверхности референц-эллипсоида по формулам, приведенным в учебнике. Затем измеренные величины редуцируют с эллипсоида на плоскость в проекции Гаусса—Крюгера по формулам сфероидической геодезии.