что такое разность событий

Операции над событиями

Определение 1. Говорят, что в некотором опыте событие А влечёт за собой появление события В, если при наступлении события А наступает и событие В. Обозначение этого определения А Ì В. В терминах элементарных событий это означает, что каждое элементарное событие, входящее в А, входит также и в В.

Определение 2. События А и В называются равными или эквивалентными (обозначается А = В), если А Ì В и В Ì А, т.е. А и В состоят из одних и тех же элементарных событий.

Достоверное событие представляется объемлющим множеством Ω, а невозможное событие – пустым подмножеством Æ в нём. Несовместность событий А и В означает, что соответствующие подмножества А и В не пересекаются: А∩В = Æ.

Определение 3. Суммой двух событий А и В (обозначается С = А + В) называется событие С, состоящее в наступлении по крайней мере одного из событий А или В (союз «или» для суммы является ключевым словом), т.е. наступает или А, или В, или А и В вместе.

Пример. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B – в том, что в мишень попадает 2-й стрелок. Событие A + Bозначает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков (1-й стрелок или 2-й стрелок, или оба стрелка).

Пример. Суммой событий А, В, С является событие, состоящее в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С, А или В, А или С, В или С, А или В или С.

Определение 4. Произведением двух событий А и В называется событие С (обозначается С = А ∙ В), состоящее в том, что в результате испытания произошли и событие А, и событие В одновременно. (Союз «и» для произведения событий является ключевым словом).

Аналогично произведением конечного числа событий А₁, А₂, …, А_n (обозначается А = А₁ ∙А₂ ∙…∙ А_n) называется событие А, состоящее в том, что в результате испытания произошли все указанные события.

Пример. Если события А, В, С есть появление «герба» в первом, во втором и третьем испытании соответственно, то событие А × В × С есть выпадение «герба» во всех трех испытаниях.

Замечание 1. Для несовместных событий А и В справедливо равенство А ∙ В = Æ, где Æ – невозможное событие.

Определение 5. Противоположными событиями называются два единственно возможных несовместных события, образующие полную группу. Событие, противоположное событию А, обозначается . Событие противоположное событию А, является дополнением к событию А до множества Ω.

Для противоположных событий одновременно удовлетворяются два условия А ∙ = Æ и А + = Ω.

Определение 6. Разностью событий А и В (обозначается А – В) называется событие, состоящее в том, что событие А наступит, а событие В – нет и оно равна А – В = А×.

Отметим, что события А + В, А ∙ В, , А – В удобно трактовать в графическом виде с помощью диаграмм Эйлера – Венна (рис. 1.1).

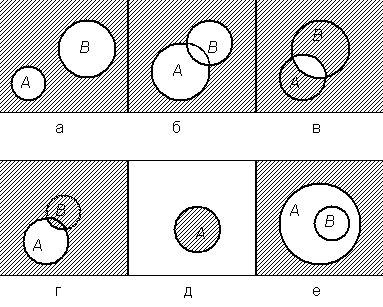
Рис. 1.1. Операции над событиями: отрицание, сумма, произведение и разность

Сформулируем пример так: пусть опыт G заключается в проведении стрельбы наугад по области Ω, точ-ки которого являются элементар-ными событиями ω. Пусть попа-дание в область Ω есть достоверное событие Ω, а попадание в области А и В – соответственно события А и В. Тогда события , А+В (или А È В – светлая область на рисунке), А ∙ В (или А Ç В – область в центре), А – В (или А \ В – светлые подобласти) будут соответствовать четырем изображениям на рис. 1.1. В условиях предыдущего примера со стрельбой двух стрелков по мишени произведением событий А и В будет событие С = А Ç В, состоящее в попадании в мишень обоими стрелками.

Замечание 3. Если операции над событиями представить как операции над множествами, а события представить как подмножества некоторого множества Ω, то сумме событий А+В соответствует объединение АÈВ этих подмножеств, а произведению событий А ∙ В — пересечение А∩В этих подмножеств.

Таким образом, операции над событиями можно поставить в соответствие операцию над множествами. Это соответствие приведено в табл. 1.1

Источник

Основные понятия теории вероятностей

Классификация событий

Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита и т.д.

Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.

Операции над событиями

При разработке аппарата и методики исследования случайных событий в теории вероятностей очень важным является понятие суммы и произведения событий.

Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

Сумма событий обозначается так:

Например, если событие есть попадание в цель при первом выстреле, событие — при втором, то событие есть попадание в цель вообще, безразлично, при каком выстреле — первом, втором или при обоих вместе.

Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Произведение событий обозначается

Например, если событие есть попадание в цель при первом выстреле, событие — при втором, то событие состоит в том, что в цель попали при обоих выстрелах.

Классическое определение вероятности случайного события

Для количественного сравнения событий по степени возможности их появления вводится числовая мера, которая называется вероятностью события.

Вероятностью события называется число, являющееся выражением меры объективной возможности появления события.

Из формулы (1.1) следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев:

Свойства вероятности

Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.

Свойство 4. Вероятность наступления противоположного события определяется так же, как и вероятность наступления, события :

Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.

Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение. Обозначим событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:

Элементы комбинаторики

Два сочетания различаются хотя бы одним элементом, а размещения различаются либо самими элементами, либо порядком их следования. Число сочетаний из элементов по вычисляется по формуле

есть число размещений из элементов по ; — число перестановок из элементов.

Пример 2. В партии из 10 деталей имеется 7 стандартных. Найти вероятность того, что среди взятых наудачу 6 деталей ровно 4 стандартных.

Статистическое определение вероятности

Формулу (1.1) используют для непосредственного вычисления вероятностей событий только тогда, когда опыт сводится к схеме случаев. На практике часто классическое определение вероятности неприменимо по двум причинам: во-первых, классическое определение вероятности предполагает, что общее число случаев должно быть конечно. На самом же деле оно зачастую не ограничено. Во-вторых, часто невозможно представить исходы опыта в виде равновозможных и несовместных событий.

Частота появления событий при многократно повторяющихся Опытах имеет тенденцию стабилизироваться около какой-то постоянной величины. Таким образом, с рассматриваемым событием можно связать некоторую постоянную величину, около которой группируются частоты и которая является характеристикой объективной связи между комплексом условий, при которых проводятся опыты, и событием.

Вероятностью случайного события называется число, около которого группируются частоты этого события по мере увеличения числа испытаний.

Это определение вероятности называется статистическим.

Преимущество статистического способа определения вероятности состоит в том, что он опирается на реальный эксперимент. Однако его существенный недостаток заключается в том, что для определения вероятности необходимо выполнить большое число опытов, которые очень часто связаны с материальными затратами. Статистическое определение вероятности события хотя и достаточно полно раскрывает содержание этого понятия, но не дает возможности фактического вычисления вероятности.

Геометрическая вероятность

В классическом определении вероятности рассматривается полная группа конечного числа равновозможных событий. На практике очень часто число возможных исходов испытаний бесконечно. В таких случаях классическое определение вероятности неприменимо. Однако иногда в подобных случаях можно воспользоваться другим методом вычисления вероятности. Для определенности ограничимся двумерным случаем.

Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.

Пример 3. Круглая мишень вращается с постоянной угловой скоростью. Пятая часть мишени окрашена в зеленый цвет, а остальная — в белый (рис. 4). По мишени производится выстрел так, что попадание в мишень — событие достоверное. Требуется определить вероятность попадания в сектор мишени, окрашенный в зелёный цвет.

Аксиомы теории вероятностей

Из статистического определения вероятности случайного события следует, что вероятность события есть число, около которого группируются частоты этого события, наблюдаемые на опыте. Поэтому аксиомы теории вероятностей вводятся так, чтобы вероятность события обладала основными свойствами частоты.

Аксиома 2. Вероятность достоверного события равна единице.

Аксиома 3. Вероятность невозможного события равна нулю.

Источник

Что такое разность событий

тБУУНПФТЙН НОПЦЕУФЧП F УПВЩФЙК, ЛПФПТЩЕ НПЦОП ОБВМАДБФШ Ч ОЕЛПФПТПН УМХЮБКОПН ЬЛУРЕТЙНЕОФЕ. рХУФШ – ДПУФПЧЕТОПЕ УПВЩФЙЕ, Б – ОЕЧПЪНПЦОПЕ, ФБЛЦЕ РТЙОБДМЕЦБФ НОПЦЕУФЧХ F.

лБЦДПНХ УПВЩФЙА б РПУФБЧЙН Ч УППФЧЕФУФЧЙЕ РТПФЙЧПРПМПЦОПЕ (ДПРПМОЙФЕМШОПЕ) УПВЩФЙЕ, ПВПЪОБЮБЕНПЕ Й ПЪОБЮБАЭЕЕ, ЮФП УПВЩФЙЕ ТЕБМЙЪХЕФУС ФПЗДБ Й ФПМШЛП ФПЗДБ, ЛПЗДБ УПВЩФЙЕ б ОЕ ТЕБМЙЪХЕФУС. чЧЕДЕН ЛБЛ БЛУЙПНЩ УМЕДХАЭЙЕ УЧПКУФЧБ ЬФПК ПРЕТБГЙЙ:

; ; .

рТЙНЕТБНЙ РТПФЙЧПРПМПЦОЩИ УПВЩФЙК НПЗХФ УМХЦЙФШ РПРБДБОЙЕ Й РТПНБИ РТЙ ЧЩУФТЕМЕ, ПФЛБЪ РТЙВПТБ Ч ДБООПН ЙОФЕТЧБМЕ ЧТЕНЕОЙ Й ЕЗП ЙУРТБЧОБС ТБВПФБ Ч ФПН ЦЕ ЙОФЕТЧБМЕ ЧТЕНЕОЙ.

дМС ЛБЦДПК РБТЩ УПВЩФЙК б Й ч ЧЧЕДЕН ПРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС.

уПВЩФЙЕ ЪБЛМАЮБАЭЕЕУС Ч ФПН, ЮФП ЙЪ ДЧХИ УПВЩФЙК б Й ч РТПЙУИПДЙФ РП ЛТБКОЕК НЕТЕ ПДОП, ОБЪЩЧБАФ ПВЯЕДЙОЕОЙЕН УПВЩФЙК б Й ч.

уПВЩФЙЕ (бч), ЪБЛМАЮБАЭЕЕУС Ч ФПН, ЮФП РТПЙУИПДСФ ПДОПЧТЕНЕООП ПВБ УПВЩФЙС б Й ч, ОБЪЩЧБАФ РЕТЕУЕЮЕОЙЕН УПВЩФЙК б Й ч.

пРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС ЛПННХФБФЙЧОЩ Й БУУПГЙБФЙЧОЩ

;
;
;
.

уМЕДХАЭЙЕ ЖПТНХМЩ ЧЧПДСФУС ЛБЛ БЛУЙПНЩ:

чЧЕДЕООЩЕ УППФОПЫЕОЙС РЕТЕОПУСФУС У ДЧХИ УПВЩФЙК ОБ РТПЙЪЧПМШОПЕ ЛПОЕЮОПЕ ОЕРХУФПЕ УЕНЕКУФЧП УПВЩФЙК .

пРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС, ОБЛПОЕГ, ДЙУФТЙВХФЙЧОЩ РП ПФОПЫЕОЙА ДТХЗ Л ДТХЗХ:

;
.

уФТХЛФХТБ, ЛПФПТБС ПВТБЪХЕФУС ОБ НОПЦЕУФЧЕ УПВЩФЙК ЧЧЕДЕООЩНЙ ПРТЕДЕМЕОЙСНЙ Й БЛУЙПНБНЙ, ОБЪЩЧБЕФУС УФТХЛФХТПК ВХМЕЧПК БМЗЕВТЩ. тБУУНПФТЙН ЧУРПНПЗБФЕМШОЩЕ РПОСФЙС, ПРТЕДЕМСЕНЩЕ ОБ ВХМЕЧПК БМЗЕВТЕ УПВЩФЙК.

дЧБ УПВЩФЙС б Й ч, ДМС ЛПФПТЩИ ОБЪЩЧБАФУС ОЕРЕТЕУЕЛБАЭЙНЙУС (ЧЪБЙНОП ЙУЛМАЮБАЭЙНЙ). пВЯЕДЙОЕОЙЕ ФБЛЙИ УПВЩФЙК ОБЪЩЧБАФ УХННПК Й ПВПЪОБЮБАФ б + ч ЧНЕУФП .

тБЪОПУФША ДЧХИ УПВЩФЙК б Й ч ОБЪЩЧБАФ УПВЩФЙЕ б – ч, УПУФПСЭЙЕ Ч ФПН, ЮФП РТПЙЪПКДЕФ УПВЩФЙЕ б Й ОЕ РТПЙЪПКДЕФ УПВЩФЙЕ ч. пЮЕЧЙДОП, ЮФП .

уЙННЕФТЙЮЕУЛПК ТБЪОПУФША ДЧХИ УПВЩФЙК б Й ч ОБЪЩЧБАФ УПВЩФЙЕ , ПЪОБЮБАЭЕЕ, ЮФП РТПЙУИПДЙФ МЙЫШ ПДОП ЙЪ б, ч.

уПВЩФЙС ПВТБЪХАФ РПМОХА ЗТХРРХ УПВЩФЙК, ЕУМЙ ПОЙ РПРБТОП ОЕ РЕТЕУЕЛБАФУС (ОЕУПЧНЕУФОЩ) Й , ФП ЕУФШ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ РТПЙУИПДЙФ ПДОП Й ФПМШЛП ПДОП ЙЪ ОЙИ.

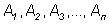
зПЧПТСФ, ЮФП УПВЩФЙЕ б ЧМЕЮЕФ УПВЩФЙЕ ч (ПВПЪОБЮБАФ ), ЕУМЙ УПВЩФЙЕ ч ПВСЪБФЕМШОП РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ УПВЩФЙС б. еУМЙ УПВЩФЙС б Й ч НПЗХФ РПСЧЙФШУС ЙМЙ ОЕ РПСЧЙФШУС ФПМШЛП ЧНЕУФЕ, ФП ЕУФШ Й , ФП ПОЙ ОБЪЩЧБАФУС ЬЛЧЙЧБМЕОФОЩНЙ (б = ч). ьЛЧЙЧБМЕОФОЩЕ УПВЩФЙС ТБЪМЙЮБФШ ОЕ ВХДЕН. пФОПЫЕОЙЕ «ЧМЕЮЕФ» СЧМСЕФУС ПФОПЫЕОЙЕН РПТСДЛБ Ч НОПЦЕУФЧЕ УПВЩФЙК.

вТПУБАЭБСУС Ч ЗМБЪБ БОБМПЗЙС НЕЦДХ УПВЩФЙСНЙ Й НОПЦЕУФЧБНЙ ПВЯСУОСЕФУС ФЕН, ЮФП ЛБЦДПЕ УПВЩФЙЕ УЧСЪБОП У ПРТЕДЕМЕООЩН НОПЦЕУФЧПН ЙУИПДПЧ ЬЛУРЕТЙНЕОФБ ФБЛ, ЮФП ПОП ПВСЪБФЕМШОП РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ ПДОПЗП ЙЪ ЙУИПДПЧ, РТЙОБДМЕЦБЭЙИ ЬФПНХ НОПЦЕУФЧХ, Й ОЕ РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ ПДОПЗП ЙЪ ЙУИПДПЧ, ОЕ РТЙОБДМЕЦБЭЙИ ЬФПНХ НОПЦЕУФЧХ. оБРТЙНЕТ, УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ ВХДЕФ ПДОП РПРБДБОЙЕ, ЕУФШ УХННБ ДЧХИ ОЕРЕТЕУЕЛБАЭЙИУС УПВЩФЙК: РПРБДБОЙЕ РТЙ РЕТЧПН Й РТПНБИ РТЙ ЧФПТПН ЧЩУФТЕМЕ Й РТПНБИ РТЙ РЕТЧПН Й РПРБДБОЙЕ РТЙ ЧФПТПН ЧЩУФТЕМЕ

.

дМС УФТПЗПЗП НБФЕНБФЙЮЕУЛПЗП ПВПУОПЧБОЙС, ЧЧПДСФ РПОСФЙЕ ЬМЕНЕОФБТОПЗП УПВЩФЙС.

ьМЕНЕОФБТОЩН УПВЩФЙЕН ОБЪЩЧБЕФУС УПВЩФЙЕ, ОЕ УПДЕТЦБЭЕЕ ОЙЛБЛЙИ РПДУПВЩФЙК, ЛТПНЕ ОЕЧПЪНПЦОПЗП УПВЩФЙС Й УБНПЗП УЕВС

ч ТБНЛБИ ЬЛУРЕТЙНЕОФБ, ЬМЕНЕОФБТОПЕ УПВЩФЙЕ ЬФП ТЕЪХМШФБФ ЬЛУРЕТЙНЕОФБ. лБЦДПЕ, ПФОПУСЭЕЕУС Л ТБУУНБФТЙЧБЕНПК НПДЕМЙ ЬМЕНЕОФБТОПЕ УПВЩФЙЕ, ЧМЕЮЕФ МЙВП ОБУФХРМЕОЙЕ, МЙВП ОЕ ОБУФХРМЕОЙЕ ЛБЦДПЗП ДБООПЗП УПВЩФЙС, УЧСЪБООПЗП У ТБУУНБФТЙЧБЕНПК НПДЕМША. оБРТЙНЕТ, РТЙ ПДОПН ЧЩУФТЕМЕ РП НЙЫЕОЙ ЬМЕНЕОФБТОЩН УПВЩФЙЕН ВХДХФ РТПНБИ Й РПРБДБОЙЕ. ч ЬЛУРЕТЙНЕОФЕ – РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ ВХДЕФ ПДОП РПРБДБОЙЕ – ЬМЕНЕОФБТОЩНЙ УПВЩФЙСНЙ ВХДХФ: РПРБДБОЙЕ РТЙ РЕТЧПН Й РТПНБИ РТЙ ЧФПТПН ЧЩУФТЕМЕ Й РТПНБИ РТЙ РЕТЧПН Й РПРБДБОЙЕ РТЙ ЧФПТПН ЧЩУФТЕМЕ.

уМХЮБКОЩК ЬЛУРЕТЙНЕОФ ОБЪЩЧБЕФУС ЛПОЕЮОЩН, ЕУМЙ ЙНЕЕФУС РПМОБС ЗТХРРБ ЬМЕНЕОФБТОЩИ УПВЩФЙК.

ч ФЕПТЙЙ ЧЕТПСФОПУФЕК ТБУУНБФТЙЧБАФУС МЙЫШ ФБЛЙЕ УМХЮБКОЩЕ ЬЛУРЕТЙНЕОФЩ, Ч ЛПФПТЩИ ЛБЦДПЕ УПВЩФЙЕ СЧМСЕФУС УХННПК ЧУЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК, ЧМЕЛХЭЙИ ЬФП УПВЩФЙЕ. фБЛПК УМХЮБКОЩК ЬЛУРЕТЙНЕОФ ПРЙУЩЧБЕФУС НОПЦЕУФЧПН ЬМЕНЕОФБТОЩН УПВЩФЙК, УЧСЪБООЩИ У ОЙН Й ОЕЛПФПТЩН ЛМБУУПН ЕЗП РПДНОПЦЕУФЧ, ОБЪЩЧБЕНЩИ УПВЩФЙСНЙ Й ОБЪЩЧБЕФУС РТПУФТБОУФЧПН ЬМЕНЕОФБТОЩИ УПВЩФЙК. пВПЪОБЮБЕФУС ПВЩЮОП . рТЙ ЬФПН МАВПЕ ЬМЕНЕОФБТОПЕ УПВЩФЙЕ – ФПЮЛБ РТПУФТБОУФЧБ ПВПЪОБЮБЕФУС ВХЛЧПК .

дПУФПЧЕТОПЕ УПВЩФЙЕ РТЕДУФБЧМСЕФ УПВПК НОПЦЕУФЧП ЧУЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК . оЕЧПЪНПЦОПЕ УПВЩФЙЕ РТЕДУФБЧМСЕФ УПВПК РХУФПЕ НОПЦЕУФЧП .

оБРТЙНЕТ, РТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК Ч ЬЛУРЕТЙНЕОФЕ, ЪБЛМАЮБАЭЕНУС Ч ФПН, ЮФП ОБВМАДБЕФУС РПРБДБОЙЕ ЙМЙ РТПНБИ РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ УПУФПЙФ ЙЪ ЮЕФЩТЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК: ДЧБ РПРБДБОЙС, РПРБДБОЙЕ – РТПНБИ, РТПНБИ – РПРБДБОЙЕ, ДЧБ РТПНБИБ.

дМС ОБЗМСДОПУФЙ РПУФТПЕООПК НБФЕНБФЙЮЕУЛПК НПДЕМЙ УМХЮБКОЩИ СЧМЕОЙК ХДПВОП ХУМПЧОП УЮЙФБФШ РТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК ОЕЛПФПТПК ПВМБУФША РМПУЛПУФЙ (ЛЧБДТБФПН), ЬМЕНЕОФБТОПЕ УПВЩФЙЕ — ФПЮЛБНЙ ЬФПК ПВМБУФЙ; РТЙ ЬФПН УПВЩФЙС ХДПВОП ЙЪПВТБЦБФШ Ч ЧЙДЕ ОЕЛПФПТЩИ ЖЙЗХТ (ЛТХЗПЧ).

оБ ТЙУХОЛБИ РТЕДУФБЧМЕОЩ ЙЪПВТБЦЕОЙС УМЕДХАЭЙИ ПРЕТБГЙК:

Б). б Й ч – ОЕУПЧНЕУФОЩЕ УПВЩФЙС;
В).— ПВЯЕДЙОЕОЙЕ УПВЩФЙК б Й ч;
Ч). бч – РЕТЕУЕЮЕОЙЕ УПВЩФЙК б Й ч;
З). б – ч – ТБЪОПУФШ УПВЩФЙК б Й ч;
Д). — РТПФЙЧПРПМПЦОПЕ Л б УПВЩФЙЕ;
Е). — УПВЩФЙЕ ч ЧМЕЮЕФ УПВЩФЙЕ б.

чБЦОЩН РТЙНЕТПН УМХЮБКОПЗП ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ЬЛУРЕТЙНЕОФ, Ч ЛПФПТПН ЙЪНЕТСЕФУС ОЕЛПФПТБС ЧЕМЙЮЙОБ и. ч ЛБЮЕУФЧЕ ЬМЕНЕОФБТОЩИ УПВЩФЙК ЪДЕУШ НПЦОП ЧЪСФШ УПВЩФЙС ЧЙДБ (и = И), ЗДЕ И – ОЕЛПФПТПЕ ЖЙЛУЙТПЧБООПЕ ЪОБЮЕОЙЕ. нОПЦЕУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК ЕУФЕУФЧЕООП ПФПЦДЕУФЧЙФШ У НОПЦЕУФЧПН ФПЮЕЛ ОБ РТСНПК. еУМЙ БРТЙПТЙ ЙЪЧЕУФОП, ЮФП и НПЦЕФ РТЙОЙНБФШ МЙЫШ ЪОБЮЕОЙС ЙЪ ОЕЛПФПТПЗП НОПЦЕУФЧБ н, ФП ЬФП НОПЦЕУФЧП Й УМЕДХЕФ ТБУУНБФТЙЧБФШ ЛБЛ НОПЦЕУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК. ч РТПГЕУУЕ ЙЪНЕТЕОЙС ЕУФЕУФЧЕООП РТЕДРПМБЗБФШ ЧПЪНПЦОПУФШ ОБВМАДЕОЙС УПВЩФЙС , ЗДЕ Б Й b – РТПЙЪЧПМШОЩЕ ЮЙУМБ. чУЕЧПЪНПЦОЩЕ ЛПОЕЮОЩЕ УХННЩ ФБЛЙИ РПМХЙОФЕТЧБМПЧ НПЦОП ТБУУНБФТЙЧБФШ ЛБЛ БМЗЕВТХ УПВЩФЙК, УЧСЪБООЩИ У ЬЛУРЕТЙНЕОФПН.

Источник