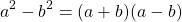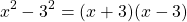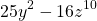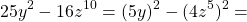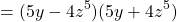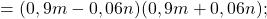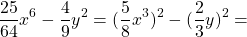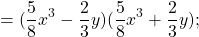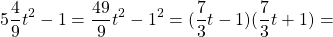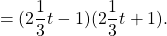что такое разность квадратов
Разность квадратов
Что такое разность квадратов
Разность квадратов двух чисел или выражений равняется сумме этих чисел/выражений, умноженной на их разность. То есть формула представляет собой разложение многочлена на множители:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Доказательство формулы разности квадратов
Арифметическое доказательство
Чтобы подтвердить справедливость определения разности квадратов, рассмотрим правую часть уравнения.
Раскроем скобки и получим:
(a+b)(a−b)=a 2 +ab−ba−b 2 =a 2 −b 2
Справедливость формулы доказана.
Геометрическое доказательство
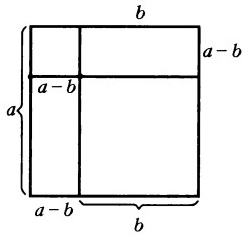
Продолжим любую прямую, на которой лежит сторона меньшего квадрата, до пересечения со стороной большего четырехугольника. В результате внутри исходного квадрата со стороной a имеем:
Теперь найдем величину, которая останется при вычитание площади меньшего квадрата из площади большего. Как видим по чертежу, она равна площадям двух образовавшихся прямоугольников, то есть:
Применение формулы разности квадратов
Формула разности квадратов в алгебре может использоваться в двух видах случаев:
Примеры прямого использования формулы и формулировка стандартной ошибки
Необходимо раскрыть скобки в выражении:
Возьмем 15m в качестве a, 12n — в качестве b, значит:
Исходя из формулы, запишем:
Подставим в полученное выражение исходные переменные:
Стандартная ошибка прямого использования формулы заключается в следующем. Если в исходном выражении переместить в начало множитель со знаком плюс, при этом поменяв местами слагаемые, то получим:
В данном варианте записи зачастую происходит путаница с уменьшаемым и вычитаемым, то есть:
Следует обратить внимание на множитель со знаком минус.
Возьмем 8f за a, 4e за b, тогда:
Учитывая возможность совершения стандартной ошибки при использовании формулы сокращенного умножения (разности квадратов), обращаем внимание на второй множитель, выраженный разностью. Чтобы применить формулу, нам необходимо поменять местами слагаемые в первом множителе. Тогда получим:
Выполним подстановку исходных переменных:
Видим, что числитель раскладывается на множители по формуле разности квадратов:
Разность квадратов: формула и примеры
В данной публикации мы рассмотрим формулу сокращенного умножения, с помощью которой можно разложить разность квадратов на множители. Также разберем примеры решения задач для закрепления изложенного материала.
Формула разности квадратов
Разность квадратов чисел/выражений a и b равна произведению их суммы на разность.
a 2 – b 2 = (a – b)(a + b)
Формулу можно представить справа-налево:
(a – b)(a + b) = a 2 – b 2
Примечание: a 2 – b 2 ≠ (a – b) 2
Доказательство формулы
Арифметическое
Геометрическое
Задача состоит в том, чтобы найти площадь фигуры голубого цвета ( a 2 – b 2 ).
Продолжив любую из линий сторон меньшего квадрата до границ большего мы получим:
Нам нужна только сумма площадей прямоугольников, которая вычисляется таким образом:
S = a ⋅ (a – b) + b ⋅ (a – b) = a 2 – ab + ba – b 2 = a 2 – b 2
Примеры задач
Решение
Применим формулу сокращенного умножения:
(8x – 3y)(8x + 3y) = 64x 2 – 9y 2
Решение
Воспользуемся формулой в обратную сторону:
25x 2 – y 2 = (5x – y)(5x + y)
Проверка
(5x – y)(5x + y) = 25x 2 + 5xy – 5xy – y 2 = 25x 2 – y 2
Сокращенное умножение: правила, формулы
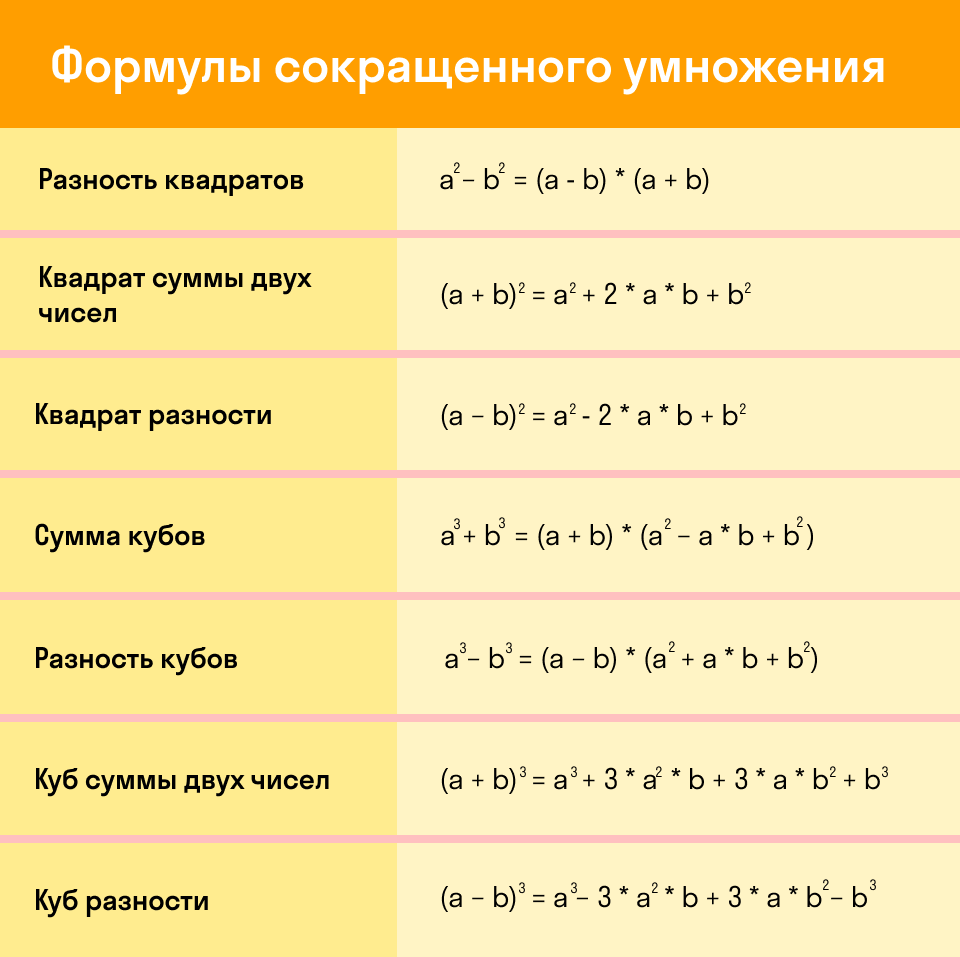
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
Доказательство формул сокращенного умножения
Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).
Для четных показателей можно записать так:
a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).
Для нечетных показателей:
a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с 3 – 8.
Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).
Задание 3
Как решаем:
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
Алгебра. 7 класс
Конспект урока
Перечень вопросов, рассматриваемых в теме:
• упрощение умножения многочленов;
• разложение многочлена на множители;
• вычисление значения числового выражения;
Теоретический материал для самостоятельного изучения.
Вы знаете формулы квадрата суммы и квадрата разности.
Сегодня мы рассмотрим ещё одну формулу и покажем её справедливость, применив это правило.
Формула разности квадратов.
Получено равенство, которое называют формулой разности квадратов.
Формулу разности квадратов используют:
• для упрощения умножения многочленов;
• для разложения многочлена на множители;
• для упрощения вычислений.
На рисунке выделена красным контуром, состоит из желтого и зеленого прямоугольников.
Площади составлены из одинаковых прямоугольников, значит, они равны.
Для преобразования выражений используют тождество:
Разбор решения заданий тренировочного модуля.
Вычисление значений числовых выражений.
В первом случае вы, вероятно, находили квадрат числа умножением в столбик, во втором случае устно.
Разность квадратов
Каждая из формул сокращенного умножения является тождеством. Это значит, что ее можно применять в обоих направлениях: и от левой части переходить к правой, и от правой — к левой. Разность квадратов — правая часть формулы произведения суммы и разности двух выражений.
Соответственно, разность квадратов двух выражений равна произведению их суммы и разности. Формула разности квадратов
На практике, как правило, выражения не представлены в виде квадратов, то есть, прежде чем воспользоваться формулой, их надо преобразовать.
Представим каждое выражение в виде квадрата, используя свойства степеней:
теперь можем разложить разность квадратов на множители:
С помощью схемы разложение разности квадратов на множители можно изобразить так:
Схему можно использовать для наглядности на начальном этапе работы с формулой.
Например, нужно разложить как разность квадратов двучлен 16a²-49b². Представим каждое из выражений в виде квадрата и воспользуемся схемой:
Еще примеры разложения многочлена на множители по формуле разности квадратов:
Чтобы представить в виде квадрата смешанное число, надо перевести его в неправильную дробь. Разложив разность квадратов на множители, неправильную дробь переводим в смешанное число, выделив целую часть
В алгебре разность квадратов — одна из самых востребованных формул сокращенного умножения.