что такое разбиение в математике

Что такое разбиение в математике

Пусть p ( n ) обозначает количество всех разбиений натурального Для небольших n легко вычислить p ( n ), просто выписав все разбиения. Например, Вот все 7 разбиений (5), (4, 1), (3, 2), (3, 1, 1), (2, 2, 1), (2, 1, 1, 1), (1, 1, 1, 1, 1). Однако получить таким способом, скажем, без помощи компьютера немыслимо. Между было известно ещё в XIX веке. Мы познакомим вас со многими интересными свойствами разбиений и научим находить не выписывая всех разбиений

Задача вычисления p ( n ) имеет почтенный возраст. Впервые она была сформулирована Лейбницем в 1654 году, а в 1740 — предложена немецким математиком Филиппом Ноде Леонарду Эйлеру. Занимаясь разбиениями, Эйлер открыл целый ряд их свойств, среди которых главное место занимала знаменитая «пентагональная теорема». С исследований Эйлера начинается история теории разбиений, в развитии которой принимали участие крупнейшие математики последующих поколений.

Две теоремы Эйлера

Изучение функции p ( n ) Эйлер начинает с рассмотрения бесконечного произведения

Каждый член произведения получается в результате умножения мономов, взятых по одному из каждой скобки. Если в первой скобке во то их произведение будет равно Значит, после раскрытия скобок получится сумма мономов вида

Посмотрим теперь на выражения в скобках. Каждое из них — бесконечная геометрическая прогрессия. По формуле суммирования

и т.д. Теперь наш результат можно записать так:

Эта формула была открыта Эйлером в 1740 году. Ряд, стоящий в левой части, называется производящей функцией последовательности чисел Производящая функция позволяет компактно записать информацию о последовательности, хотя извлечение этой информации из производящей функции порой требует большого искусства. Сейчас вы увидите, как это делал Эйлер.

Обозначим через d ( n ) количество разбиений числа n на различные слагаемые, а через l ( n ) — на нечётные. Например, среди выписанных выше разбиений различные части а нечётные — и Значит,

Такие же рассуждения, как при выводе формулы (1), позволяют выписать производящие функции последовательностей

В правой части равенства все числители сокращаются со знаменателями, содержащими x в чётной степени. Поэтому в знаменателе останутся только сомножители вида Итак,

Значит, производящие функции последовательностей d ( n ) совпадают! Мы доказали теорему Эйлера : Это доказательство хорошо иллюстрирует силу метода производящих функций.

Но вернёмся к вычислению p ( n ). Изучая производящую функцию последовательности Эйлер сосредоточил внимание на произведении знаменателе правой части Раскрывая в нём скобки, Эйлер получил удивительный результат:

Пентагональная теорема оказалась «крепким орешком» — Эйлер сумел доказать её лишь 14 лет спустя. Эта теорема позволяет сравнительно просто вычислять Вот как это делается.

и воспользуемся пентагональной теоремой:

Пользуясь формулой Эйлера, можно составить таблицу для что и проделал в начале известный английский специалист по комбинаторике майор В то время это была наиболее полная таблица

Итак, мы сформулировали две теоремы, одну из — доказали. Согласитесь, что при всей элегантности этого доказательства, оно всё же оставляет чувство неудовлетворённости. Два множества разбиений — на нечётные и на неравные части — неожиданно оказались состоящими из одинакового числа элементов, но причина этого равенства осталась скрытой от нас. Хотелось бы думать, что существует естественный способ каждому элементу одного множества ставить в соответствие элемент другого.

Соответствия Глэйшера и Сильвестра

Приведём ещё два доказательства теоремы Эйлера:

Первое соответствие между разбиениями на различные слагаемые и разбиениями на нечётные слагаемые строится так:

Например, разбиению (6, 2, 1) соответствует разбиение (3, 3, 1, 1, 1). Это остроумное соответствие придумано в конце XIX века английским математиком Дж. Глэйшером.

Чтобы доказать взаимную однозначность соответствия Глэйшера, достаточно построить обратное соответствие между разбиениями с нечётными частями и разбиениями с неравными частями. Вот это соответствие:

Пусть в разбиении некоторая нечётная часть r встречается k раз. Запишем k в виде суммы различных степеней двойки

и заменим на То, что получится, будет разбиением с различными частями.

Например, разбиение (5, 5, 5, 1, 1, 1, 1, 1, 1) соответствует разбиению (10, 5, 4, 2), поскольку число пятёрок равно а число единиц равно

Существует другое, не менее интересное и совершенно неожиданное доказательство теоремы Эйлера, принадлежащее американскому математику XIX века Дж. Сильвестру. Вот конструкция Сильвестра: пусть имеется разбиение на нечётные части: где На листе клетчатой бумаги в некотором её узле поставим Справа поставим в узлах и столько же точек поставим в узлах, расположенных под Затем проделаем то же самое с взяв в качестве исходной расположенную в следующем за по диагонали направо вниз узле, пока не дойдём до

Например, разбиению на нечётные части (9, 9, 5, 1, 1) будет отвечать картинка, изображённая на рис. 1.

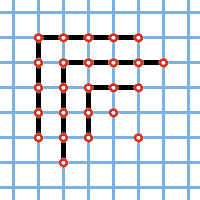Рис. 1.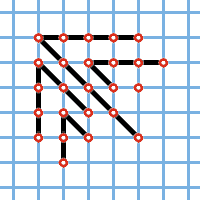

Рис. 2.

В нашем примере получится разбиение (9, 6, 5, 4, 1). Подумайте, как построить по разбиению на различные части разбиение на нечётные, т.е. восстановить по такому разбиению исходную симметричную картинку.

Отступление: решение задачи М1065

В этом разделе используется более сложная техника, чем в остальной части статьи. При желании вы можете пробежать его, не вникая в детали, и продолжить чтение со следующего раздела. Итак, займёмся решением задачи М1065 из «Задачника «Кванта» Напомним её формулировку.

Решение задачи начнём с того, что найдём общий вид целочисленных решений неравенства Числа и имеют одинаковую чётность, поэтому является чётным при любых Следовательно, для любого достаточно найти целочисленные решения уравнения Положим Тогда Из этих двух равенств немедленно получаем:

где q — любое целое число, а

Смысл чисел m и q станет более наглядным, если представлять себе векторы как точки с целыми координатами параболы лежащей в плоскости (Вы понимаете, почему это парабола?) Тогда полученные нами целочисленные решения неравенства показывают, что все точки с целыми координатами, лежащие на параболе и внутри неё, получаются сдвигами целых точек этой параболы на векторы (рис. 3). Удобно считать, что — номер параболы, на которой лежит a — номер точки на этой параболе.

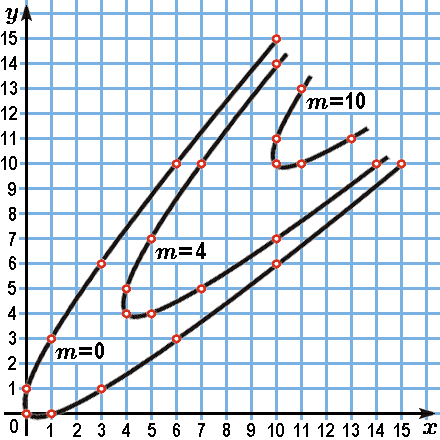
Рис. 3.

Поскольку условия задачи симметричны относительно перестановки координат векторов, достаточно доказать все утверждения для таких векторов что т.е. для векторов

Докажем достаточность условия в задачи. По формуле суммы арифметической прогрессии

Доказать необходимость условия тоже несложно. Пусть

Для такого вектора

(здесь мы снова воспользовались формулой суммы арифметической прогрессии). Из следует, что и вообще Поэтому — вектор что и требовалось доказать.

В геометрических терминах означает, что зависит лишь от параболы и не зависит от точки на параболе.

Такую пару мы будем записывать в виде

Рассмотрим отображение φ множества в множество заданной формулой

Чтобы доказать, что φ — взаимно однозначное отображение, построим обратное отображение прочитав правило, слева направо:

Построенные отображения взаимно обратны, поэтому φ — взаимно однозначное соответствие. Значит, что и утверждалось.

Чтобы научиться вычислять значения установим связь между числами

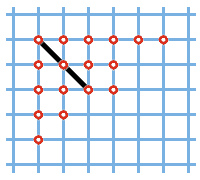
Рис. 4.

Проведём на диаграмме Юнга диагональ — чёрная линия на рис. 4. Пусть точек в первой строке, лежащих на диагонали и справа от неё, точек второй строки, лежащих на диагонали и справа от неё, точек первого столбца под диагональю, точек второго столбца под диагональю Поставим в соответствие диаграмме Юнга, изображающей разбиение пару последовательностей

Теперь ничего не стоит ответить и на последний вопрос задачи — о значении Поскольку лежит на третьей параболе. Значит,

Следующие упражнения — на применение диаграмм Юнга.

Решая задачу М1065, мы проделали большую работу. Нельзя ли снова воспользоваться производящими функциями и извлечь из равенства какое-нибудь красивое тождество?

Заменяя произведение на по мы преобразуем левую

и мы получаем следующую формулу:

Эти две формулы получены Гауссом. Нечего и говорить, что это удивительно красивые формулы!

В заключение я хочу познакомить вас с двумя знаменитыми тождествами теории разбиений, для которых до сих пор не найдено прозрачных доказательств, хотя эта задача и по сей день остаётся в сфере интересов многих математиков.

Конечно, закономерность, утверждаемая этими тождествами, в высшей степени красива и нетривиальна, и неудивительно, что крупнейший английский математик начала XX века Г. Харди, узнавший о них из письма Рамануджана, датированного 16 января 1913 года, пришёл в восхищение. *)

При чтении этой статьи у вас, может быть, сложилось впечатление, будто теория разбиений напоминает кунсткамеру, в которую заботливо собраны различные экзотические экспонаты, никак или почти никак между собой не связанные. До недавнего времени так оно и было. Ситуация коренным образом изменилась лишь в XX века, когда английскому математику Яну Макдональду удалось найти единый подход к доказательству большого класса тождеств теории разбиений и открыть много новых, объединив их в стройную теорию (тождество Гаусса–Якоби включается в неё). **) Для тождеств Роджерса–Рамануджана и многих аналогичных тождеств общего подхода не найдено, хотя в последнее время и появились алгебраические методы их доказательств. Так что, понимание истинной природы этих тождеств, вероятно, ещё впереди.

Источник

Разбиение числа

Разбие́ние числа́ n — это представление n в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие от композиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В канонической записи разбиения части перечисляются в невозрастающем порядке.

Число разбиений натурального числа n является одним из фундаментальных объектов изучения в теории чисел.

Содержание

Примеры

Например, или — разбиения числа 5, поскольку . Всего существует p(5)=7 разбиений числа 5: , , , , , , .

Некоторые значения числа разбиений (последовательность A000041 в OEIS) приведены в следующей таблице:

Число разбиений

Производящая функция

Последовательность числа разбиений имеет следующую производящую функцию:

Эта формула была открыта Эйлером в 1740 году.

Пентагональная теорема Эйлера

Изучая производящую функцию последовательности , Эйлер сосредоточил внимание на её знаменателе, то есть, на произведении . Это бесконечное произведение при раскрытии скобок приобретает следующий вид:

Показатели степеней x в правой части — это пятиугольные числа, то есть, числа вида где q — целое число, а знак при равен .

Согласно этому наблюдению Эйлер предположил, что должна быть верна Пентагональная теорема:

.

Впоследствии эта теорема была Эйлером доказана. Она позволяет вычислять числа разбиений при помощи деления формальных степенны́х рядов.

Асимптотические формулы

Асимптотическое выражение для количества разбиений было получено Харди и Рамануджаном и впоследствии уточнено Радемахером. Оригинальное выражение Харди — Рамануджана [источник не указан 48 дней]

при

дает, например, . Уточнение Радемахера представляет число разбиений в виде сходящегося ряда

Здесь суммирование ведется по , взаимно простым с , а — сумма Дедекинда. Ряд сходится очень быстро.

Рекуррентные формулы

Количество разбиений числа n на слагаемые, не превышающие k, удовлетворяет рекуррентной формуле:

n, \end» border=»0″ />

с начальными значениями:

для всех 0″ border=»0″ />

При этом количество всевозможных разбиений числа n равно .

Количество разбиений натурального числа n на k слагаемых удовлетворяет рекуррентной формуле:

с начальными значениями:

i.» border=»0″ />

Конгруэнтности

Диаграммы Юнга

Разбиения удобно представлять в виде наглядных геометрических объектов, называемых диаграммами Юнга, в честь английского математика Альфреда Юнга. Диаграмма Юнга разбиения — подмножество первого квадранта плоскости, разбитое на ячейки, каждая из которых представляет собой единичный квадрат. Ячейки размещаются в строки, первая строка имеет длину , над ней расположена строка длиной , и т. д. до -ой строки длины . Строки выровнены по левому краю.

Более формально, диаграмма Юнга — это замыкание множества точек таких, что

0″ border=»0″ /> и

где обозначает целую часть .

В англоязычной литературе диаграммы Юнга часто изображают отражёнными относительно оси абсцисс.

Схожий объект, называемый диаграммой Ферре, отличается тем, что

Применение

Разбиения естественным образом возникают в ряде математических задач. Наиболее значимой из них является теория представлений симметрической группы, где разбиения естественно параметризуют все неприводимые представления. Суммы по всем разбиениям часто встречаются в математическом анализе.

См. также

Литература

Полезное

Смотреть что такое «Разбиение числа» в других словарях:

Разбиение — В математике Разбиение единицы Разбиение множества Разбиение интервала Разбиение числа … Википедия

Разбиение единицы — Разбиение единицы конструкция, используемая в топологии для удобства работы с многообразием как множеством карт. С помощью разбиения единицы определяется, в частности, интеграл от дифференциальной формы на многообразии. Конструкция Пусть… … Википедия

Разбиение графа — Пример разбиения параллельной граф схемы алгоритма логического управления. В составе блоков, отмеченных разными цветами, нет параллельных вершин Разбиение графа на подграфы (англ. Graph partition) (иногда в литературе также употребляется… … Википедия

Разбиение Аммония — Таблицы канонов Евсевия (окончание первого канона). Латинская рукопись Евангелий, V в. Апостольская библиотека, Ватикан (Vat. Lat. 3806. F° 2v.) Страница из Ватиканского кодекса 354, Евангелия от Луки (Лк 17:34 18:8), написанного поздним… … Википедия

Композиция числа — У этого термина существуют и другие значения, см. Композиция. Не следует путать с Композиция функций. В теории чисел композицией, или разложением, натурального числа называется его представление в виде упорядоченной суммы натуральных слагаемых.… … Википедия

Вещественные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия

Действительные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия

Реальные числа — Вещественные, или действительные[1] числа математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.… … Википедия

КЛЕТОЧНОЕ РАЗБИЕНИЕ — CW комплекс, клеточный комплекс X, удовлетворяющий следующим условиям: (С) Для любой точки комплекс X(х)является конечным, т. е. состоит из конечного числа клеток (для произвольного подмножества А клеточного комплекса Xчерез X(А)обозначается… … Математическая энциклопедия

ЛОКАЛЬНОЕ РАЗБИЕНИЕ — свойство расположения замкнутого множества Ф в пространстве заключающееся в существовании такой точки а(точка, в к рой множество Ф разбивает пространство) и такого положительного числа что при любом числе в открытом множестве где (открытый) шар… … Математическая энциклопедия

Источник

РАЗБИЕНИЕ

— 1) Р.- представление заданного множества в виде объединения системы множеств, не имеющих попарно общих точек.

В дискретной геометрии часто рассматривают Р. нек-рого пространства на замкнутые области, к-рые покрывают все пространство и попарно не имеют общих внутренних точек (граничные точки могут быть общими). Напр., если зафиксировать любую точечную решетку евклидова пространства и сопоставить каждой точке решетки те точки пространства, к-рые удалены от этой точки не более, чем от любой другой точки решетки, то получается т. н. разбиение Д и р и х л е- В о р о н о г о. Р. пространства наз. правильным, если для любых его областей D 1 и D 2 существует такое движение M, что D 2 =M(D 1 ). и Р=М (Р). См. также Вороного типы решеток.

В комбинаторной геометрии имеется ряд задач и результатов, относящихся к специальным Р. нек-рых множеств. Примером такой задачи является Барсука проблема:можно ли разбить любое множество диаметра d, лежащее в , на n+1 таких частей, что каждая из них имеет диаметр

Полезное

Смотреть что такое «РАЗБИЕНИЕ» в других словарях:

разбиение — партиция, разделение, подразделение, разложение (на множество членов), декомпозиция; рассечение; членение, разбивание, расчленение, разбивка, подразбиение, раздробление, дробление, размежевка, размежевание Словарь русских синонимов. разбиение сущ … Словарь синонимов

разбиение — РАЗБИТЬ, зобью, зобьёшь; бей; итый; сов. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

разбиение — Разделение процесса на параллельные и независимые фрагменты; программы на модули. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики электросвязь,… … Справочник технического переводчика

Разбиение — В математике Разбиение единицы Разбиение множества Разбиение интервала Разбиение числа … Википедия

разбиение — skaidinys statusas T sritis radioelektronika atitikmenys: angl. partition; subdivision vok. Abteilung, f; Unterteilung, f rus. разбиение, n; разложение, n pranc. partition, f … Radioelektronikos terminų žodynas

разбиение — разби ение, я … Русский орфографический словарь

разбиение — 1. Syn: партиция, разделение, подразделение, разложение (мат., на множество членов), декомпозиция (матем.) 2. Syn: рассечение … Тезаурус русской деловой лексики

Разбиение — Компания разбивает переводимые средства на отдельные потоки для определенных целей. См. Bundling … Инвестиционный словарь

Разбиение интервала — [a, b] на вещественной оси это конечная последовательность вида a = x0 Википедия

Разбиение единицы — Разбиение единицы конструкция, используемая в топологии для удобства работы с многообразием как множеством карт. С помощью разбиения единицы определяется, в частности, интеграл от дифференциальной формы на многообразии. Конструкция Пусть… … Википедия

Источник