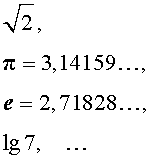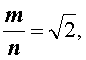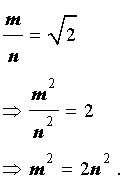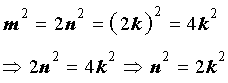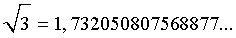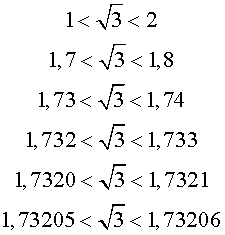что такое рациональное число и иррациональное число в математике
Числа: натуральные, целые, рациональные, иррациональные, действительные
Натуральные числа
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
сочетательное свойство сложения
переместительное свойство умножения
сочетательное свойство умножения
распределительное свойство умножения
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
Подробнее об иррациональных числах в разделе Иррациональные числа.
Действительные числа
Действительные числа – это все рациональные и все иррациональные числа.
Множество действительных чисел обозначается латинской буквой R.
Рациональные и иррациональные числа. Множество действительных чисел
Понятие рационального числа
Примеры рациональных чисел:
Любое рациональное число представимо в виде конечной или периодической бесконечной десятичной дроби.
Алгоритм перевода десятичной периодической дроби в обыкновенную дробь
Для смешанной периодической дроби – в знаменателе записать столько девяток, сколько цифр в периоде и справа дописать столько нулей, сколько цифр в дробной части до периода.
Шаг 3. Если необходимо, сократить полученную дробь
Чистые периодические дроби:
Смешанные периодические дроби:
Иррациональные числа
Примеры иррациональных чисел:
Множество иррациональных чисел не замкнуто относительно операции сложения.
Мера иррациональности действительного числа a – действительное число μ, которое показывает, насколько хорошо число a может быть приближено рациональными числами.
$μ(a) = 1 \iff a$ – рациональное число
Для многих трансцендентных чисел мера иррациональности неизвестна, есть только верхняя оценка.
Алгебраические и трансцендентные числа
Если действительное число является корнем уравнения вида
Алгебраические числа бывают рациональными и иррациональными.
Примеры трансцендентных чисел:$ π,2^<\sqrt2>, sin10^0, e^4$
Все трансцендентные числа иррациональны.
Т.е., трансцендентных чисел «больше», чем алгебраических. Их слишком много, чтобы можно было представить в виде последовательности.
Структура множества действительных чисел
Из-за несовпадения подмножеств, структуру множества действительных чисел можно представить двумя равносильными схемами:
Множество действительных чисел несчётно.
Множество действительных чисел замкнуто относительно операций сложения, вычитания, умножения и деления (исключая деление на 0).
В алгебре говорят, что действительные числа образуют непрерывное упорядоченное поле.
Примеры
Пример 1. Найдите рациональные дроби, равные данным бесконечным периодическим десятичным дробям:
Понятие о вещественных (действительных) числах, рациональные и иррациональные числа
Содержание
 Рациональные и иррациональные числа. Понятие о вещественных числах Рациональные и иррациональные числа. Понятие о вещественных числах |
 Иррациональность числа Иррациональность числа 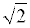 |
 Десятичные приближения иррациональных чисел с недостатком и с избытком Десятичные приближения иррациональных чисел с недостатком и с избытком |
Рациональные и иррациональные числа. Понятие о вещественных числах
Каждое из рациональных чисел можно представить в виде

где m – целое число, а n – натуральное число.
и т.п. являются примерами иррациональных чисел.
Иррациональные числа нельзя представить в виде дроби, числитель которой является целым числом, а знаменатель натуральным числом.
При обращении иррациональных чисел в десятичные дроби получаются бесконечные непериодические десятичные дроби. Множество иррациональных чисел бесконечно.
Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.
Иррациональность числа 
Проведем доказательство иррациональности числа 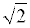
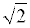

и такая, у которой числитель и знаменатель являются натуральными числами, не имеющими простых общих делителей.
Используя данное равенство, получаем:
Отсюда вытекает, что число n 2 является четным, а, значит, и число n является четным числом.
Итак, число m является четным, и число n является четным, значит, число 2 является общим делителем числителя и знаменателя дроби

Полученное противоречие доказывает, что несократимой дроби, удовлетворяющей соотношению
не существует. Следовательно, число 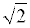
Десятичные приближения иррациональных чисел с недостатком и с избытком
Разберем понятие десятичных приближений иррациональных чисел с недостатком и с избытком на конкретном примере. Для этого рассмотрим иррациональное число
Это число, как и любое другое иррациональное число, изображается бесконечной непериодической десятичной дробью.
Последовательностью десятичных приближений числа 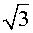
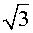
Само число 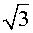
Для числа 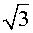
Точно также можно построить последовательность десятичных приближений с недостатком и с избытком для любого иррационального числа.
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №15. Действительные числа.
Перечень вопросов, рассматриваемых в теме
1) множество иррациональных чисел;
2) множество рациональных чисел;
3) правила выполнения действий с бесконечными десятичными дробями;
4)определение бесконечно убывающей геометрической прогрессии.
Иррациональные числа— это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.
Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.
Все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).
Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.
Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Все числа, которые мы изучаем в школе, называются действительными числами. Они образуют множество действительных чисел, которые принято обозначать латинской буквой R.
В свою очередь все действительные числа можно разделить на 2 группы: рациональные числа и иррациональные числа.
Иррациональные числа— это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.
Рациональные числа, в свою очередь, можно разделить на 2 вида – это целые числа и дробные числа.
Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.
Целые же числа можно разделить еще на несколько групп: отрицательные целые числа, нуль и положительные (натуральные) целые числа.
На числовой оси (Ох) между целыми числами будут находиться дробные иррациональные числа. Все вместе они будут представлять собой множество действительных чисел, R.
Обратите внимание, что все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).
Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.
Числа 4; 4,2; 4,28 и т.д. являются последовательными приближениями значений суммы

Пусть 



Читается «модуль разности у и 

Т.е. если 

Модуль действительного числа у обозначается как |у| и определяется так же, как и модуль рационально числа:

А теперь давайте вспомним, что такое геометрическая прогрессия.
Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего (Рисунок 1).
В результате, мы получили последовательность сторон квадратов 

И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,
n=15, 
n=20, 
n=21, 
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников. (рисунок 2)
Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.
То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.
Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.
Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.
Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
Используя данное определение можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: 
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.
По формуле суммы n первых членов геометрической прогрессии, она равна
Если n неограниченно возрастает, то
или 


Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности
Например, для прогрессии 

имеем
Так как 
Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле
Примеры и разборы решений заданий тренировочного модуля
Пример 1:
Найдем значение данного выражения с точностью до единиц.
Округлим полученные результаты до десятых:
Найдем значение данного выражения с точностью до десятых.
Округлим полученные результаты до сотых:

Найдем значение данного выражения с точностью до сотых.
Округлим полученные результаты до тысячных:


Давайте выясним, является ли последовательность бесконечно убывающей геометрической прогрессией, если она задана формулой:
а) 



Следовательно, данная геометрическая прогрессия является бесконечно убывающей.
Следовательно, данная последовательность не является бесконечно убывающей геометрической прогрессией.