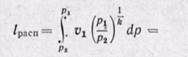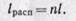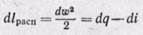что такое располагаемая работа

Располагаемая работа при истечении газа

Величинаравная бесконечно малому приращению внешней

кинетической энергии рабочего тела, называется элементарной рас­полагаемой работой. Эта энергия может быть использована для полу­чения внешней полезной работы.

Из сравнения уравнений (5-12) и (13-3) следует, что для обрати­мого процесса течения газа

(13-7)

Равенство (13-7) показывает, что при движении рабочего тела по каналу знаки dw и dp противоположны. Если dp>0, то газ сжи­мается, и его скорость будет уменьшаться dw 0.

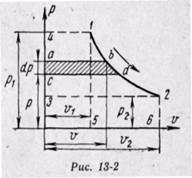
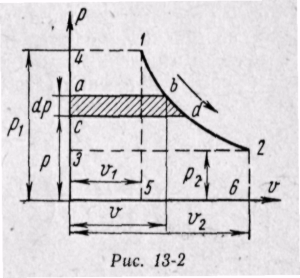
Располагаемую работу при истечении газа можно представить графически на рv-диаграмме. На рис. 13-2 изображен обратимый процесс расширения газа 1-2.

Бесконечно малая располагаемая работа — vdp измеряется элементарной площадкой abdc. Очевидно, вся располагаемая рабо­та в процессе 1-2 будет равна

(13-8)

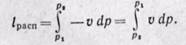
Отсюда приращение кинетической энергии потока газа (распола­гаемая работа) равно работе внешних сил (p₁v₁) плюс работа рас­ширения в процессе 1-2 и минус работа (p₂v₂), затраченная газом на преодоление сопротивления среды, в которую газ вытекает. Она измеряется пл. 1234, ограниченной линией процесса расширения газа, абсциссами крайних точек и осью ординат (р).

Если кривая 1-2 является политропой, то располагаемую работу определяют из уравнения

При адиабатном расширении иде­ального газа

(13-10)

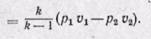
Сравнивая располагаемую рабо­ту при

истечении (пл. 1234) с ра­ботой расширения газа (пл. 1265), получаем, что величина распо­лагаемой работы в n раз больше работы расширения газа:

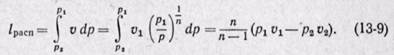
Из уравнения (13-3) следует, что

Располагаемая работа при течении газа может быть получена за счет внешнего тепла и уменьшения энтальпии газа. Это уравне­ние справедливо как для обратимых, так и для необратимых про­цессов течения газа с трением.

При адиабатном течении из уравнения (13-5)

(13-11)

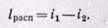
При необратимом истечении газа располагаемая работа при том же перепаде давления будет меньше.

Дата добавления: 2015-04-15 ; просмотров: 1827 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Располагаемая работа

При истечении газа

Величина 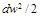, равная бесконечно малому приращению внешней кинетической энергии рабочего тела, называется элементарной располагаемой работой. Эта энергия может быть использована для получения внешней полезной работы.

Из сравнения уравнений (4.8) и (10.6) следует, что для обратимого процесса течения газа

. (10.10)

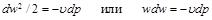
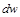
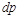
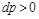
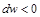
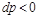
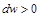
Равенство (10.10) показывает, что при движении рабочего тела по каналу знаки и противоположны. Если , то газ сжимается и его скорость уменьшается: .

Если , то газ расширяется и его скорость увеличивается: .

Эта закономерность лежит в основе специальных каналов переменного сечения, называемых соплами и диффузорами.

Если при перемещении газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называется соплом.

Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называется диффузором.

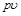
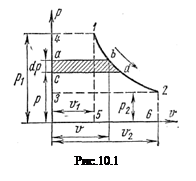
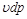
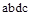
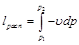
Располагаемую работу при истечении газа можно представить графически на -диаграмме. На рис. 10.1 изображен обратимый процесс расширения газа 1-2.

Бесконечно малая располагаемая работа – измеряется элементарной площадкой . Очевидно, вся располагаемая работа в процессе 1–2 равна

. (10.11)

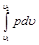
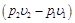
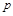
Приращение кинетической энергии потока газа (располагаемая работа), как это следует из (4.8) и (10.6) представляет собой разность работ расширения потока газа и работы проталкивания . Располагаемая работа l_расп измеряется пл. 1234, ограниченной линией процесса расширения газа, абсциссами крайних точек и осью ординат .

Если кривая 1–2 является политропой, то располагаемую работу определяем из уравнения

(10.12)

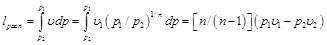
При адиабатном расширении идеального газа

. (10.13)

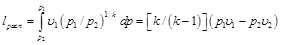
Сравнивая располагаемую работу при истечении (пл. 1234) с работой расширения газа (пл.1265), получаем, что величина располагаемой работы в n раз больше работы расширения газа:

.

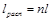
Из уравнения (10.4) следует, что

.

. (10.14)

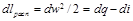
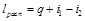
Располагаемая работа при течении газа может быть получена за счет внешней теплоты и уменьшения энтальпии газа. Это уравнение справедливо как для обратимых, так и для необратимых процессов течения газа с трением.

При адиабатном течении из уравнения (10.14)

,

. (10.15)

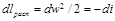
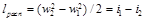
Из уравнения (10-15), принимая w₁≈0 найдём скорость истечения

. (10.16)

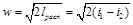
Дата добавления: 2020-07-18 ; просмотров: 212 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Располагаемая работа газа в потоке

Располагаемая работа газа в потоке

Осборн Рейнольдс впервые показал, что существуют два основных режима движения: ламинарный и турбулентный. Людмила Фирмаль

То есть в обратимом процессе увеличение скорости всегда связано с уменьшением давления, а в обратном случае уменьшение скорости сопровождается увеличением давления. Канал, через который происходит расширение газов, при уменьшении давления (ip 0) и увеличении скорости (wp> 0) называется соплом. Канал, в котором газ сжимается с увеличением давления (dr> 0) и уменьшением скорости (yi> 0), называется диффузионным. Золма. Как видно из уравнения(10.13), необходимым условием для получения доступной работы является перепад давления. Речь идет только о pp. Если во время процесса давление постоянно yp = 0, то доступная работа равна y /₀= 0.

Тот факт, что пограничный слой делит поток на зоны и, таким образом, вносит изменение в режим основного ядра потока, будет подробнее рассматриваться ниже. Людмила Фирмаль

В общем случае одноразовая работа может быть или не быть больше продолжительной работы, но это соотношение равно. Литропический процесс, при котором работа расширения газа определяется уравнением Сравнение с имеющейся работой приводит к равенству FН = Н1. Способ адиабатического расширения газа В случае изолированного потока газа доступная работа может также определяться энтальпией газа. Используя уравнение(10.13)、 ты » = — Си. Если вы интегрируете эту формулу、 1₀= — ^Λ = (1₁-y. (10.15). Таким образом, работа газов, имеющихся в адиабатическом потоке, будет равна разнице между энтальпией начального и конечного состояний.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Располагаемая работа

Политропный процесс описывается уравнением

Для данного процесса показатель политропы п является величиной посто­янной.

Из уравнения политропы и уравнения состояния нетрудно получить выраже­ния, устанавливающие связь между р, v и Т влюбых двух точках на политропе.

Внешняя работа процесса

Количество подведенной (или отве­денной) в процессе теплоты можно опре­делить с помощью уравнения первого закона термодинамики:

где теплоёмкость политропного процесса

	Процесс п с Изохорный ±∞ cv Изобарный cр Изотермный ∞ Адиабатный k Политропный п cnол
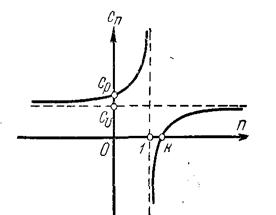
Рис. 4.5. Зависимость теплоёмкости от показателя политропы	Рис.4.6. Значения теплоёмкостей для разных процессов

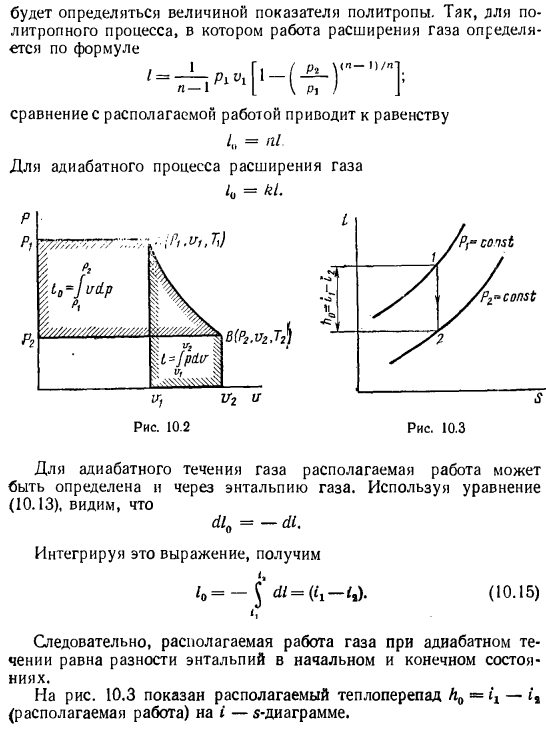
На рис. 4-5 приведена зависимость теплоёмкости от показателя политропы, из которого следует, что при n = 1 функция теплоёмкости терпит разрыв, при n k – вновь положительна.

Изменение внутренней энергии

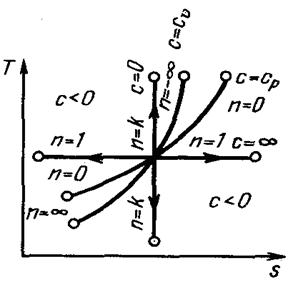Рис. 4.7. Изображение основных термоди­намических процессов идеального газа в Т, s-координатах

Изменение энтальпии

Изменение энтропии

Политропный процесс имеет обобща­ющее значение, ибо охватывает со­вокупность четырёх основных термодинамических процессов.

На рис. 4.7 показано взаимное распо­ложение на Т, s-диаграммах политропных процессов с разными значения­ми показателя политропы. Все процессы начинаются в одной точке («в центре»).

Адиабата и изотерма делит поле диаграммы на четыре квадранта. Изохора (п= ± оо) и изобара проходят через второй и четвёртый квадранты. Процессы, нахо­дящиеся правее изохоры, характеризу­ются положительной работой, так как сопровождаются расширением рабочего тела; для процессов, расположенных ле­вее изохоры, характерна отрицательная работа.

Процессы, расположенные правее адиабаты, идут с подводом теп­лоты к рабочему телу; процессы, лежа­щие левее адиабаты, протекают с отводом теплоты.

Для процессов, расположенных над изотермой (n = 1), характерно увеличе­ние

внутренней энергии газа; процессы, расположенные под изотермой, сопро­вождаются уменьшением внутренней энергии.

Процессы, расположенные между адиабатой и изотермой, имеют отрица­тельную

теплоемкость, так как q и du (а следовательно, и dT), имеют в этой области противоположные знаки. В таких процессах |l| > |q|, поэтому на произ­водство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела.

Исторически политропная модель термодинамического процесса возникла в конце XIX столетия как результат обобщения классических термодинамических процессов, открытых в XVII – XIX столетиях. Обобщённая модель была получена путём формального распространения значений показателей степени конкретных процессов на числовую ось ± ∞ при сохранении условия с = пост.

Давно установлено, что применительно к ДВС уравнения политропных процессов лишь приближённо отражают особенности реальных процессов сжатия и расширения и совсем не годятся для описания процесса сгорания. Во всех учебных пособиях много места занимают объяснения причин отклонений в протекании политропных и реальных процессов.

Объяснить несовершенство для применения при расчётах процессов в ДВС, основное развитие которых относится к значительно более позднему периоду, можно, главным образом, несоответствием характером подвода и отвода теплоты от рабочего тела при политропном и реальном процессе.

Широко освоенный метод определения показателя политропы n по индикаторным диаграммам [12], показал, что показатель n является переменной величиной, как в процессе сжатия, так и в процессах сгорания и расширения.

Сравнение показателя политропы с показателем адиабаты позволило объяснять динамику тепловых потоков в течение отдельных процессов реального цикла, которая противоречила расчётам по уравнениям политропных процессов. Иллюстрацией могут служить данные, полученные при индицировании четырехтактного компрессорного тихоходного двигателя с самовоспламенением (n = 226 об/мин, ε = 14) производства фирмы Зульцер и приведенные в изданном в 1953 году учебном пособии Мелькумова [16]). На графике рис. 1 приведена индикаторная диаграмма, там же нанесены кривые переменных значений показателя n₁ на ходе сжатия и показателя n₂ линии конечной фазы сгорания и фазы расширения.

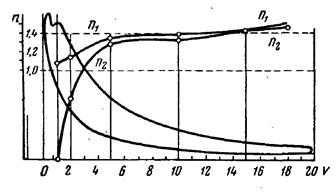Рис. 1. Изменение показателей политроп для линий сжатия и расширения в четырехтактном двигателе Зульцер.

Подобное изменение n₂ на графике могло также означать только одно: величина с в реальных газовых процессах изменяется: от с_v при изохоре и с_р при изобаре до ± ∞ при изотерме и последующем снижении до нуля при адиабате. Таким образом, можно утверждать, что к 1935 году наличие в газовых процессах двигателей внутреннего сгорания феномена с = var было доказано экспериментально.

Известно, что (Вукалович, стр 74) при изменении состояния идеального газа по политропе от температуры Т₁ до температуры Т₂ количество теплоты, подводимой или отводимой от газа, определяется выражением

. (1)

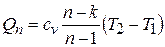
Из представленной зависимости следует, что количество теплоты при заданном n однозначно определяется разностью между показателями политропы и адиабаты, а такжеразностью температур между начальной и конечной точками процесса. Указанная зависимость также не отражает влияние температуры на величину показателя адиабаты. теплоёмкость политропного процесса

Исследование реальных процессов в двигателе показало, что удовлетворительное совпадение теоретического и реального процессов удаётся достичь только в случае изменения величины n в ходе процесса, что отражено в уравнениях термотропного процесса.

Источник

Располагаемая работа при истечении газа

Величинаравная бесконечно малому приращению внешней

кинетической энергии рабочего тела, называется элементарной рас­полагаемой работой. Эта энергия может быть использована для полу­чения внешней полезной работы.

Из сравнения уравнений (5-12) и (13-3) следует, что для обрати­мого процесса течения газа

(13-7)

Равенство (13-7) показывает, что при движении рабочего тела по каналу знаки dw и dp противоположны. Если dp>0, то газ сжи­мается, и его скорость будет уменьшаться dw 0.

Располагаемую работу при истечении газа можно представить графически на рv-диаграмме. На рис. 13-2 изображен обратимый процесс расширения газа 1-2.

Бесконечно малая располагаемая работа — vdp измеряется элементарной площадкой abdc. Очевидно, вся располагаемая рабо­та в процессе 1-2 будет равна

(13-8)

Отсюда приращение кинетической энергии потока газа (распола­гаемая работа) равно работе внешних сил (p₁v₁) плюс работа рас­ширения в процессе 1-2 и минус работа (p₂v₂), затраченная газом на преодоление сопротивления среды, в которую газ вытекает. Она измеряется пл. 1234, ограниченной линией процесса расширения газа, абсциссами крайних точек и осью ординат (р).

Если кривая 1-2 является политропой, то располагаемую работу определяют из уравнения

При адиабатном расширении иде­ального газа

(13-10)

Сравнивая располагаемую рабо­ту при

истечении (пл. 1234) с ра­ботой расширения газа (пл. 1265), получаем, что величина распо­лагаемой работы в n раз больше работы расширения газа:

Из уравнения (13-3) следует, что

Располагаемая работа при течении газа может быть получена за счет внешнего тепла и уменьшения энтальпии газа. Это уравне­ние справедливо как для обратимых, так и для необратимых про­цессов течения газа с трением.

При адиабатном течении из уравнения (13-5)

(13-11)

При необратимом истечении газа располагаемая работа при том же перепаде давления будет меньше.

Критическая скорость и максимальный секундный расход идеального газа

Скорость газа, которая устанавливается в выходном сечении суживающегося канала при истечении газа в окружающую среду с давлением, равным или ниже критического называется крити­ческой скоростью.

Критическую скорость можно определить из уравнения (13-14),

подставив в него вместо значение

(13-19)

Критическая скорость при истечении идеального газа зависит только от начальных параметров и его природы.

Можно доказать, что критическая скорость равна скорости зву­ка в газе при критических параметрах р_к и v_к.

Из адиабатного процесса следует

Из уравнения (13-17) находим или

Умножив правую и левую части уравнения на p₁, получим

Подставив значение p₁ v₁ в формулу (13-19), получим значе­ние w_к:

после преобразований будем иметь

(13-20)

Из физики известно, что величина определяет скорость звука в газе в выходном сечении суживающегося канала, или критическая скорость при истечении газа равна местной скорости звука (в данном сечении).

Последнее позволяет объяснить, почему в суживающемся канале газ не может расширяться до давления меньше критического, а скорость не может превысить критическую. Дей­ствительно, как известно из физики, импульс давления распространяется в материальной среде со скоростью звука, и поэтому, когда скорость ис­течения будет меньше скорости зву­ка (критической скорости), уменьше­ние внешнего давления передается по потоку газа внутрь канала и при­водит к перераспределению давления в канале. В результате в вы­ходном сечении канала устанавливается давление, равное давлению среды. Если же скорость истечения достигнет скорости звука (кри­тической скорости), то скорость движения газа и скорость распро­странения давления будут одинаковы и никакое уменьшение внеш­него давления не сможет повлиять на распределение давлений внут­ри канала. Оно будет постоянным, а следовательно, будет неизмен­ным, и давление в выходном сечении канала независимо от величины внешнего давления.

Отсюда следует, что скорость истечения в выходном сечении су­живающегося канала не может быть больше местной скорости звука в газе (рис. 13-6).

При критическом давлении в выходном сечении канала устанав­ливается максимальный секундный расход газа, который опреде­ляем из уравнения (13-16) при замене на значение его из урав­нения (13-17).

После соответствующих преобразований получаем

(13-21)

Максимальный секундный расход газа вполне

определяется начальным состоянием газа, величиной

сечения f_мин и природой идеального газа, т. е.

показателем адиабаты k.

Сопло́ — канал переменного поперечного сечения, предназначенный для разгона жидкостей или газов до определенной скорости и придания потоку требуемого направления.

Принцип действия сопла основан на непрерывном увеличении скорости жидкости или газа в направлении течения от входного до выходного сечения. Для обеспечения течения жидкости (газа) необходим перепад давления с превышением его на входном сечении.

В простейшем случае сопло представляет собой цилиндрический или конический патрубок, один конец которого присоединён к источнику жидкости или газа, а из другого истекает струя.

В зависимости от скорости истечения жидкости или газа различают дозвуковое и сверхзвуковое сопло. Для дозвукового сопла характерно равенство давлений на выходе сопла и в окружающей среде. В таком сопле при возрастании давления на входе сопла и постоянном давлении окружающей среды скорость в выходном сечении сначала увеличивается, а затем при определенном значении входного давления становится постоянной и не изменяется при дальнейшем увеличении давления на входе. При этом скорость истечения равна местной скорости звука и называетсякритической.

Сопло Лаваля (сверхзвуковое) состоит из двух участков — сужающегося, предназначенного для ускорения потока до местной скорости звука, и расширяющегося, предназначенного для ускорения потока до сверхзвуковой скорости. Самое узкое поперечное сечение сверхзвукового сопла называют критическим.

Широко используется на некоторых типах паровых турбин и является важной частью современных ракетных двигателей и сверхзвуковых реактивных авиационных двигателей.

Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами. Эффективные сопла современных ракетных двигателей профилируются на основании газодинамических расчётов.

Рис. 1. Схема дозвукового сопла.

Рис. 2. Схема сверхзвукового сопла (сопла Лаваля).

Из уравнения состояния идеального газа, и баланса энергии в газовом потоке выводится формула расчёта линейной скорости истечения газа из сопла Лаваля: [1]

(4)

— Скорость газа на выходе из сопла, м/с,

— Абсолютная температура газа на входе,

— Универсальная газовая постоянная Дж/(киломоль·К),

— молярная масса газа, кг/киломоль,

— Показатель адиабаты ,

— Удельная теплоёмкость при постоянном давлении, Дж/(киломоль·К),

— Удельная теплоёмкость при постоянном объеме, Дж/(киломоль·К),

— Абсолютное давление газа на выходе из сопла, Па

— Абсолютное давление газа на входе в сопло, Па

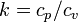
Диффузор (в аэрогидродинамике) — часть канала (трубы), в которой происходят замедление (расширение) потока и увеличение давления. При скоростях, не превышающих скорости звука, площадь поперечного сечения Д. вдоль потока возрастает, а при сверхзвуковых скоростях уменьшается. Существует конструкция, обратная диффузору, называемая конфузор — часть канала, в которой происходит соединение и плавный переход большего сечения в меньшее. Движение воздуха в конфузоре характеризуется тем, что динамическое давление в нём в направлении движения потока увеличивается, а статическое — уменьшается. Увеличивается скорость течения жидкости или газа.

Эже́ктор — (фр. éjecteur, от éjecter — выбрасывать от лат. ejicio) — гидравлическое устройство, в котором происходит передача кинетической энергии от одной среды, движущейся с большей скоростью, к другой. Эжектор, работая по закону Бернулли, создаёт в сужающемся сечении пониженное давление одной среды, что вызывает подсос в поток другой среды, которая затем переносится и удаляется от места всасывания энергией первой среды.

Эжекторы используются в струйных насосах, например водоструйных, жидкостно-ртутных, паро-ртутных, паромасляных.

Дата добавления: 2018-02-15 ; просмотров: 1503 ; Мы поможем в написании вашей работы!

Источник