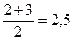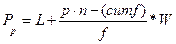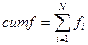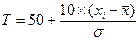что такое ранжирование в статистике

Правило ранжирования

1. Построить вариационный ряд (расположить данные первичного ряда в порядке возрастания)

2. Пронумеровать значения вариационного ряда, начиная с меньшего значения. Меньшему значению присваивается первый номер

3. Рядом со значением записать его ранг, при этом:

а) если значение в вариационном ряду встречается единственный раз, то ранг равен порядковому номеру;

б) если значение в вариационном ряду встречается два или более раз, то ранг вычисляется как среднее из порядковых номеров, которые присвоены этому значению.

4. Правильность ранжирования можно проверить. Сумма рангов должна совпадать с расчетной:

где N – количество значений в ранжируемом вариационном ряду.

Индивидуальные значения переменной «Х»: 2, 5, 6, 2, 5, 1, 3, 4, 4, 4.

Вариационный ряд «Х»: 1, 2, 2, 3, 4, 4, 4, 5, 5, 6

Данные вариационного ряда нумеруются. Определяется ранг значения, при этом, меньшему значению присваивается ранг равный единице. Значение «1» встречается в вариационном ряду единственный раз и имеет порядковый номер равный «1». Поэтому ранг значения «1» равен порядковому номеру, то есть R(1)=1. Значение «2» встречается в вариационном ряду два раза. Поэтому, ранг значения «2» вычисляется как среднее из порядковых номеров, на которых располагается это значение.

R(2)=

Значение «3» в вариационном ряду встречается единственный раз, поэтому ранг равен порядковому номеру. Ранг значения «3» равен четырем, то есть R(3)=4.

Сумма рангов должна совпадать с расчетной:

= =1+2,5+2,5+4+6+6+6+4,5+4,5+10

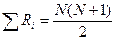
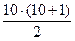
Процентиль – это процентная доля индивидов из выборки стандартизации, первичный результат которых ниже данного первичного показателя. Процентили показывают относительное положение каждого индивида в нормативной выборке, а не величину различия между результатами.

99 возможных процентилей (Р₁. Р₉₉) делят множество наблюдений на 100 частей с равным числом наблюдений в каждой.

Например, если 28% людей правильно решают 15 задач в тесте на арифметическое мышление, то первичному показателю 15 соответствует 28-й процентиль (Р₂₈).

Процентили указывают на относительное положение индивида в выборке стандартизации. Их также можно рассматривать как ранговые градации, общее число которых равно 100, с той разницей, что при ранжировании принято начинать отсчет сверху, то есть с лучшего члена группы, получающего ранг 1. В случае процентилей отсчет ведется снизу, так что, чем ниже процентиль, тем хуже позиция индивида.

Процентили не следует смешивать с обычными процентными показателям. Последние являются первичными показателями и представляют собой процент правильно выполненных заданий, тогда как процентиль – это производный показатель, указывающий на долю от общего числа членов группы. Первичный результат, который ниже любого показателя, полученного в выборке стандартизации, имеет нулевой процентильный ранг (Р₀). Результат, превышающий любой показатель в выборке стандартизации, получает процентильный ранг 100 (Р₁₀₀). Эти процентили, однако, не означают нулевого или абсолютного выполнения теста.

Перед началом вычисления любого процентиля в группе оценок надо упорядочить эти оценки по возрастанию. Для больших групп это непроизводительно и удобнее использовать сгруппированные данные.

Общая формула определения Р_р -го процентиляв группе n оценок

W – ширина интервала оценок

Накопленные частотык любой заданной оценке представляют собой суммарное количество частот на этой оценке или ниже ее.

Переход в шкалу Т-баллов:

Где, x_i-индивидуальное (i-е значение); 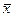— среднее арифметическое; σ-стандартное отклонение.

Источник

Ряды распределения. Атрибутные и вариационные ряды распределения. Ранжирования ряда. Характеристики варианта, частота, непрерывность, дискретность. Интервал

Поможем написать любую работу на аналогичную тему

Важнейшей частью статистического анализа является построение рядов распределения (структурной группировки) с целью выделения характерных свойств и закономерностей изучаемой совокупности. В зависимости от того, какой признак (количественный или качественный) взят за основу группировки данных, различают соответственно типы рядов распределения.

Если за основу группировки взят качественный признак, то такой ряд распределения называют атрибутивным (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.).

Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд.

Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд.

Очень часто таблица дополняется графой, в которой подсчитываются накопленные частоты S, которые показывают, какое количество единиц совокупности имеет значение признака не большее, чем данное значение.

Частоты ряда f могут заменяться частостями w, выраженными в относительных числах (долях или процентах). Они представляют собой отношения частот каждого интервала к их общей сумме, т.е.:

При построении вариационного ряда с интервальными значениями прежде всего необходимо установить величину интервала i, которая определяется как отношение размаха вариации R к числу групп m:

Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние. Если средняя арифметическая рассчитывается на основе использования всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное среднее положение в ранжированном вариационном ряду.

Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10) медианой будет величина, которая расположена в центре ряда, т.е. пятая величина.

Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин.

То есть для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле

Численное значение медианы определяют по накопленным частотам в дискретном вариационном ряду. Для этого сначала следует указать интервал нахождения медианы в интервальном ряду распределения. Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений.

Численное значение медианы

Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой.

Чтобы найти конкретное значение моды, необходимо использовать формулу

Мода имеет широкое распространение в маркетинговой деятельности при изучении покупательского спроса, особенно при определении пользующихся наибольшим спросом размеров одежды и обуви, при регулировании ценовой политики.

Основной целью анализа вариационных рядов является выявление закономерности распределения, исключая при этом влияние случайных для данного распределения факторов. Этого можно достичь, если увеличивать объем исследуемой совокупности и одновременно уменьшать интервал ряда. При попытке изображения этих данных графически мы получим некоторую плавную кривую линию, которая для полигона частот будет являться некоторым пределом. Эту линию называют кривой распределения.

Иными словами, кривая распределения есть графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, которое функционально связано с изменением вариант. Кривая распределения отражает закономерность изменения частот при отсутствии случайных факторов. Графическое изображение облегчает анализ рядов распределения.

Известно достаточно много форм кривых распределения, по которым может выравниваться вариационный ряд, но в практике статистических исследований наиболее часто используются такие формы, как нормальное распределение и распределение Пуассона.

Нормальное распределение зависит от двух параметров: средней арифметической и среднего квадратического отклонения . Его кривая выражается уравнением

Если нужно получить теоретические частоты f’ при выравнивании вариационного ряда по кривой нормального распределения, то можно воспользоваться формулой

При помощи этой формулы мы получаем теоретическое (вероятностное) распределение, заменяя им эмпирическое (фактическое) распределение, по характеру они не должны отличаться друг от друга.

Тем не менее в ряде случаев, если вариационный ряд представляет собой распределение по дискретному признаку, где при увеличении значений признака х частоты начинают резко уменьшаться, а средняя арифметическая, в свою очередь, равна или близка по значению к дисперсии (), такой ряд выравнивается по кривой Пуассона.

Кривую Пуассона можно выразить отношением

При выравнивании эмпирических данных теоретические частоты можно определить по формуле

Сравнивая полученные величины теоретических частот f’ c эмпирическими (фактическими) частотами f, убеждаемся, что их расхождения могут быть весьма невелики.

Объективная характеристика соответствия теоретических и эмпирических частот может быть получена при помощи специальных статистических показателей, которые называют критериями согласия.

Для оценки близости эмпирических и теоретических частот применяются критерий согласия Пирсона, критерий согласия Романовского, критерий согласия Колмогорова.

Наиболее распространенным является критерий согласия К. Пирсона , который можно представить как сумму отношений квадратов расхождений между f’ и f к теоретическим частотам:

Если , то расхождения между эмпирическими и теоретическими частотами распределения могут быть случайными и предположение о близости эмпирического распределения к нормальному не может быть отвергнуто.

Если вышеуказанное отношение 3, то расхождения могут быть достаточно существенными и гипотезу о нормальном распределении следует отвергнуть.

Критерий согласия А.Н. Колмогорова используется при определении максимального расхождения между частотами эмпирического и теоретического распределения, вычисляется по формуле

По таблицам значений вероятностей -критерия можно найти величину , соответствующую вероятности Р. Если величина вероятности Р значительна по отношению к найденной величине , то можно предположить, что расхождения между теоретическим и эмпирическим распределениями несущественны.

Необходимым условием при использовании критерия согласия Колмогорова является достаточно большое число наблюдений (не меньше ста).

Источник

Ранжирование (группировка, классификация) данных.

Данные, полученные в результате выборки, представляют собой «сырой» материал. Обычно перед тем, как приступить к вычислению характеристик выборки, его подвергают предварительной обработке. Наиболее распространенным методом такой обработки является ранжирование (группировка, классификация) данных. Эта процедура состоит в том, что мы все данные разбиваем на группы (ранги), и в дальнейшем всем результатам, отнесенным к одной группе, присваивается одно и то же значение (один и тот же ранг, если речь идет о качественном признаке). Например, так происходит при шитье на фабрике мужских костюмов – всех мужчин, чей рост находится в диапазоне 168-178 см., относят к одной группе(2-й рост) и всех их рассматривают как людей одного роста: 173см.

Этот метод применяется отнюдь не только в тех случаях, когда необходимость группировки данных диктуется потребностями стандартизации. Так поступают в очень многих случаях поскольку такой подход не только упрощает процедуру расчета, но и позволяет снизить влияние случайных небольших ошибок.

При разбиении всего множества вариант на группы (классы, ранги) стирается разница между дискретными и непрерывными величинами. Отметим сразу, что при работе с реальными данными непрерывных случайных величин не существует уже хотя бы потому, что любые измерения производятся с некоторой точностью, а значит любая непрерывная величина в результатах опыта предстает как дискретная, и в роли минимально возможного различия (шага дискретизации) выступает цена деления прибора.

С другой стороны, если максимальное число возможных значений дискретной случайной величины (максимальное минус минимальное значение, деленное на шаг измерения) очень велико, принципиальное различие между дискретной и непрерывной случайной величиной исчезает.[5] Т.е. практически при работе с конкретными данными имеет смысл говорить не о непрерывных и дискретных величинах, а о совокупностях данных с малым и большим числом градаций.

Способы разбиения и границы интервалов

Когда мы осуществляем группировку, мы фактически все множество возможных значений разбиваем на интервалы, и все значения, попавшие в один интервал, заменяем одним стандартнымзначением – центром интервала. При этом границы интервала определяются как средние арифметические между величинами двух соседних центров.

Отметим, что при группировке количественных характеристик, центральные значения групп всегда образуют прогрессию. Однако не всегда эта прогрессия арифметическая, иногда разумно считать что центры групп образуют геометрическую прогрессию. Последнее встречается в тех случаях, когда отношение наименьшего и наибольшего значения очень велико (ситуация большого динамического диапазона). Кроме того, геометрическая прогрессия для центров групп достаточно часто встречается в экономике потому, что для экономических задач весьма характерно «процентное» рассмотрение: результат вычисляется как некая доля исходных данных (прибыль, доход, налог – все они описываются чаще всего как доли или проценты). В случае, когда интервалы образуют арифметическую прогрессию, мы говорим о равномерной шкале, а в случае геометрической прогрессии о логарифмической шкале.

Пусть нам дана таблица данных

Легко заметить, что наши стандартизованные значения Х образуют арифметическую прогрессию, т.е. перед нами равномерная шкала. В группу со стандартным значением 270 при этом попали все значения, у которых в ходе опыта были получены результаты, лежащие в диапазоне 240 500Количество n72345422815

Здесь вполне очевидно, что центры групп образуют геометрическую прогрессию со знаменателем 1,33 (логарифмическая шкала). В группу со стандартным значением 280 при этом попали все значения, у которых в ходе опыта были получены результаты, лежащие в диапазоне 240

Распределение вариант и распределение средних. Выборочные характеристики как оценки характеристик генеральной совокупности. Свойства оценок: несмещенность, состоятельность, эффективность.

Обычно ситуация не бывает столь простой, как мы ее представили в п.1. Чаще всего мы не располагаем всей генеральной совокупностью данных и поэтому лишены возможности точно вычислить основные характеристики генеральной совокупности: генеральное среднее µ и стандартное отклонение σ. Приходится производить некоторые выборки из генеральной совокупности и на основании полученных таким образом данных вычислять не сами характеристики генеральной совокупности, а некие их оценки.

Обычно используемые оценки генерального среднего, генеральной дисперсии и стандартного отклонения по выборочным данным описываются такими формулами:

(1.3)

Обратите внимание: в этих формулах n есть объём выборки, а не генеральной совокупности.

Разумеется, желательно, чтобы наши формулы давали «хорошие» оценки, но для этого прежде всего следует ввести некие характеристики оценок, позволяющие судить, какие оценки хороши, а какие нет. Обычно используют три таких характеристики: несмещённость, состоятельность и эффективность.

Несмещённость. Если матожидание оценки совпадает с генеральным средним (или матожиданием случайной величины), оценка называется несмещенной.

Состоятельность. Если предел оценки по вероятности равен оцениваемому значению, то оценка называется состоятельной. Несколько упрощая ситуацию, можно сказать, что состоятельной называется такая оценка, которая дает практически точное значение, если используемая выборка достаточно велика и представительна.

Эффективность оценки определяется не предельным, а актуальным значением разброса оценок: из двух оценок величины более эффективна та у которой меньше дисперсия, а значит ее плотность распределения более «сжата».

Для того, чтобы правильно понимать смысл приведенных здесь характеристик нужно отчетливо представлять себе следующее. Как только мы начинаем рассматривать выборку, хотя бы только одну, мы сразу должны рассматривать ситуацию с точки зрения двух распределений: исходного распределения значений переменной х (распределение вариант) и распределения выборочных средних. Последнее трактуется следующим образом.

Пусть мы сделали не одну, а очень много выборок одинакового объёма n из одной и той же генеральной совокупности и для каждой из них вычислили среднее значение. Вполне очевидно, что различные выборки – пусть они одного объема, осуществлялись по одному принципу и в одинаковых условиях – вот у таких схожих выборок средние величины и стандартные отклонения окажутся все-таки различными. Причем различия эти продиктованы случайными причинами, поскольку случайным образом отбирались представители генеральной совокупности, попавшие в выборку, а это означает, что сами выборочные средние и выборочные стандартные отклонения являются случайными величинами. Поскольку такие выборочные средние сами есть случайные величины, мы можем построить распределение выборочных средних по данным многих выборок.

Распределение средних отличается такими важными особенностями:

а) Распределение средних при росте объёма выборки по форме стремится к нормальному распределению, независимо от того, каким по форме было распределение вариант. Т.е. оно постепенно становится близким к нормальному, даже если исходное распределение вариант сильно ассиметрично (например, экспоненциальное). Однако понятно, что для гладких, одновершинных и симметричных распределений практическая близость к нормальному будет наступать раньше, при меньших объемах выборки;

б) чем больше объем выборки n, тем более вытянутым по вертикали и сжатым по горизонтали оказывается кривая распределения выборочных средних, на рис.2б показаны кривые распределения для выборок из одной и той же генеральной совокупности, содержащих по 5 и по 12 элементов;

в) отметим, что выборочное среднее является несмещенной и эффективной оценкой генерального среднего µ.

Несмещенность оценки означает, что если по кривой распределения выборочных средних найти для случайной величины ее матожидание , то оно совпадет с матожиданием генеральной совокупности µ (на рис.2б распределение вариант симметрично, симметричны и оба распределения средних; ось симметрии у всех трех распредлений общая, что и указывает на равенство = µ). Можно показать, что существует много несмещенных оценок для матожидания генеральной совокупности µ, однако они обладают различной эффективностью.

А вот эффективность как оценки µ означает, что среди всех несмещенных оценок µ именно имеет наименьшую дисперсию.

Таким образом, несмещенной и эффективной оценкой стандартного отклонения в распределении средних является величина ,[7] т.е. матожидание величины совпадает с : M[ ] = , причем из всех оценок с таким матожиданием имеет наименьшую дисперсию

г) Стандартное отклонение в распределении средних всегда будет меньше стандартного отклонения для распределения вариант (встретить на улице человека выше 190см много вероятнее, чем встретить 20 человек, средний рост которых более 190см); причем чем больше объем выборки, тем меньше стандартное отклонение в распределении средних; точная зависимость величины стандартного отклонения от объема выборки приведена ниже

Итак, пусть мы располагаем данными полученными всего из одной выборки, все равно мы можем получить оценку характеристик генеральной совокупности на основе этой единственной выборки. При этом мы рассматриваем эти данные двояко: как описание нашей выборки, представленное таблицей; по этой таблице мы можем вычислить и σ для данной выборки. И одновременно как одну из точек на кривой распределения , этот подход будет активно использоваться при построении доверительных интервалов.

Отметим еще одно важное следствие. Выборочное среднее является несмещенной оценкой генерального среднего µ, а вот выборочное стандартное отклонение является смещенной оценкой генерального стандартного отклонения, несмещенной оценкой (см. 1.3) является s: ; нетрудно заметить, что

Источник