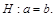что такое ранг в статистике
07.3. Примеры статистических моделей и гипотез, ранги и ранжирование
Ранги. Во многих случаях имеющиеся в нашем распоряжении числовые данные (например, значения элементов выборки) носят в той или иной мере условный характер. Например, эти данные могут быть тестовыми баллами, экспертными оценками, данными о вкусовых или политических предпочтениях опрошенных людей и т. д. Анализ таких данных требует особой осторожности, поскольку многие предпосылки классических статистических методов (например, предположения о каком-либо конкретном, скажем нормальном, законе распределения) для них не выполняются. Твердую основу для выводов здесь дают только соотношения между наблюдениями типа «больше-меньше», так как они не меняются при изменении шкалы измерений. Например, при анализе анкет с данными о симпатиях избирателей к политическим деятелям мы можем сказать, что политик, получивший больший балл в анкете, более симпатичен отвечавшему на вопросы человеку (респонденту), чем политик, получивший меньший балл. Но на сколько (или во сколько раз) он более симпатичен, сказать нельзя, так как для предпочтений нет объективной единицы измерения.
В подобных случаях (которые мы будем более подробно рассматривать в последующих главах), имеет смысл вообще отказаться от анализа конкретных значений данных, а исследовать только информацию об из взаимной упорядоченности. Для этого от исходных числовых данных осуществляют переход к их Рангам.
Определение. Рангом наблюдения называют тот номер, который получит это наблюдение в упорядоченной совокупности всех данных — после их упорядочения по определенному правилу (например, от меньших значений к большим или наоборот).
Чаще всего упорядочение чисел (набор которых составляют упомянутые выше данные) производят по величине — от меньших к большим. Именно такое упорядочение и связанное с ним ранжирование (присвоение рангов) мы будем иметь в виду в дальнейшем.
Пример. Пусть выборка состоит из чисел 6, 17, 14,5, 12. Тогда рангом числа 6 оказывается 2, рангом 17 будет 5 и т. д.
Определение. Процедура перехода от совокупности наблюдений к последовательности их рангов называется ранжированием. Результат ранжирования называется ранжировкой.
Статистические методы, в которых мы делаем выводы о данных на основании их рангов, называются ранговыми. Они получили широкое распространение, так как надежно работают при очень слабых предположениях об исходных данных (не требуя, например, чтобы эти данные имели какой-либо конкретный закон распределения). В последующих главах этой книги мы рассмотрим применение ранговых методов в наиболее распространенных практических задачах.
Средние ранги. Трудности в назначении рангов возникают, если среди элементов выборки встречаются совпадающие. (Так часто бывает, когда данные регистрируются с округлением.) В этом случае обыкновенно используют Средние ранги.
Средние ранги вводятся так. Предположим, что наблюдение 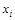
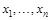
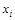
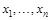
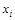
В качестве примера рассмотрим выборку 6, 17, 12, 6, 12. Ее ранжировка равна 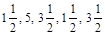
Покажем на примерах, как может проходить математическая формализация практических задач и как сформулированные на естественном языке вопросы превращаются в статистические гипотезы.
Тройной тест. Рассмотрим распространенный в психологии тройной тест (его другое название — тест дегустатора). Он состоит из серии одинаковых опытов, в каждом из которых испытуемому предъявляют одновременно три стимула. Два из них идентичны, а третий несколько отличается. Испытуемый, ориентируясь на свои ощущения, должен указать этот отличающийся стимул. Например, испытуемому могут быть предложены три стакана с жидкостью: два с чистой водой, а третий — со слабым раствором сахара, либо наоборот — два стакана подслащенных, а третий — с чистой водой. Задание для испытуемого — указать стакан, отличающийся от двух других.
Опыты стараются организовать так, чтобы они проходили в одинаковых условиях и чтобы в каждом из них испытуемый мог полагаться только на свои ощущения. В результате подобного однократного эксперимента можно получить как правильный, так и неправильный ответ.
При слабой концентрации раствора, когда его трудно отличить от воды, из одного ответа нельзя сделать определенного заключения о способности испытуемого чувствовать данную концентрацию. Испытуемый может случайно ошибиться, даже если в целом он способен отличать данную концентрацию сахара от чистой воды. С другой стороны, правильный ответ не исключает того, что испытуемый его просто угадал, не отличая раствора от воды.
Эти свойства эксперимента мы можем перечислить в виде следующих допущений:
• в каждом испытании ответ испытуемого случаен;
• существует вероятность правильного ответа, которая неизменна во все время испытаний;
• результаты отдельных испытаний статистически независимы.
Коротко это выражается так: статистической моделью эксперимента служит схема Бернулли.
Сформулировав математическую модель явления, перейдем к выдвижению статистических гипотез. Интересующая нас способность испытуемого характеризуется вероятностью правильного ответа, которую мы обозначим Р. В этом опыте она нам неизвестна. Естественно, эта вероятность зависит от степени концентрации сахара. Если концентрация очень мала и не воспринимается, то у испытуемого нет оснований для выбора. Он «наудачу» будет указывать один из трех стаканов. В этих условиях вероятность правильного ответа 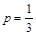
Предположим, что экспериментатора интересует, начиная с каких концентраций испытуемый отличает раствор от воды. Тогда для данной концентрации экспериментатор может выдвинуть предположение, что испытуемый ее ощутить не в состоянии. В изложенной модели это предположение превращается в статистическую гипотезу о том, что 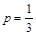
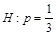
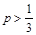
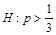
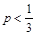
Экспериментатор может выдвигать и другие гипотезы о способности испытуемого к различению концентраций. Например, возможна такая гипотеза: испытуемый способен ощутить присутствие сахара, ошибаясь один раз из десяти. В этом случае вероятность правильного ответа равна 0.9 и гипотеза примет вид: Н : р = 0.9.
Заметим, что с чисто математической точки зрения гипотеза вида 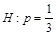
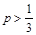
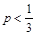
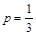
Сейчас мы не будем рассматривать процесс проверки этих гипотез (он описан в п. 4), а вместо этого приведем еще один пример перевода естественнонаучной задачи на статистический язык, т. е. построения статистической модели явления и выдвижения гипотезы для проверки.
Парные наблюдения. На практике часто бывает необходимо сравнить два способа действий по их результатам. Речь может идти о сравнении двух методик обучения, эффективности двух лекарств, производительности труда при двух технологиях и т. д. В качестве конкретного примера рассмотрим эксперимент, в котором выясняется, на какой из сигналов человек реагирует быстрее: на свет или на звук.
Эксперимент был организован следующим образом. Каждому из семнадцати испытуемых в случайном порядке поочередно подавались два сигнала: световой и звуковой. Интенсивность сигналов была неизменна в течение всего эксперимента. Увидев или услышав сигнал, испытуемый должен был нажать на кнопку. Время между сигналом и реакцией испытуемого регистрировал прибор. Результаты эксперимента приведены в табл. 1.
Время реакции на свет и на звук, в миллисекундах
I — номер испытуемого, I = 1. 17; Xi — время его реакции на звук, YI — время его реакции на свет.
Вместо поставленного выше вопроса о том, на какой из сигналов человек отвечает быстрее, выдвинем другой: можно ли считать, что время реакции человека на свет и на звук одинаковы? Логически эти вопросы тесно связаны: если мы отвечаем отрицательно на второй из них, мы тем самым признаем, что различия есть. После этого уже не трудно понять, когда время реакции меньше. Если же на второй вопрос мы отвечаем положительно, то первый после этого просто снимается. С математической же точки зрения второй вопрос проще, как мы увидим из дальнейшего обсуждения.
Итак, время реакции на звук, X, и время реакции на свет, Y, различно у разных людей, несмотря на то, что во время опыта они находились в одинаковых условиях. Ясно, что наблюдаемый разброс во времени реакции не связан с изучаемым явлением (различием двух действий). По-видимому, этот разброс можно объяснить различиями между испытуемыми и/или нестабильностью времени отклика на сигнал у каждого испытуемого. Как бы то ни было, эти колебания не имеют отношения к той закономерности, что нас интересует. Поэтому мы объявляем их случайными. Так сделан первый шаг к статистической модели: переменные Xi и Yi признаны реализациями случайных величин, скажем Xi и Yi. Поскольку каждый испытуемый решал свои задачи самостоятельно, не взаимодействуя с другими испытуемыми и не испытывая с их стороны влияния, мы будем считать случайные величины X1, Y1. Х17, Y17 Независимыми (в теоретико-вероятностном смысле).
Если экспериментатор уверен, что группа испытуемых достаточно однородна, он может дополнительно предположить, что 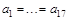
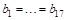
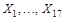
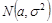
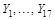
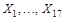
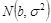
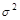
Ясно, что задача с меньшим числом неопределенных параметров, как во второй постановке, в принципе должна давать более точные ответы. При проверке гипотез это означает, что мы сможем принять или отвергнуть проверяемую гипотезу с большей степенью уверенности. Но следует помнить, что уменьшение количества параметров в модели является следствием принятия дополнительных предположений об имеющихся данных. Так, в приведенном выше примере мы предположили, что 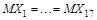
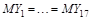
Итак, при построении статистической модели постоянно приходится вводить упрощающие математические предположения и одновременно оценивать, насколько они приемлемы с содержательной точки зрения. И часто надо быть готовым к тому, чтобы отказаться от недопустимых предположений или заменить их чем-то другим.
Другой путь построения статистической модели — так называемый Непараметрический. Здесь мы не делаем предположений о том, что наблюдаемые случайные переменные имеют какой-либо параметрический закон распределения. В этом случае мы делаем меньше математических допущений, а значит, здесь меньше опасности принять неоправданное предположение. Зато при этом мы используем не всю информацию об имеющихся данных, а только ту ее часть, которая не зависит от конкретного вида распределения исходных данных. Например, при проверке гипотезы о равном времени реакции на свет и звук мы должны будем использовать не сами значения времен реакций Xi и Yi, а их Ранги В объединенной выборке Xi и Yi. По сравнению с параметрическим методом (если предположения о параметрическом характере случайных событий справедливы), мы получим при этом несколько менее точные выводы, но зато непараметрический метод имеет гораздо более широкую область применимости.
Итак, при построении статистической модели приходится делать ряд предположений. Большую часть этих предположений мы не проверяем (и часто даже и не можем проверить). Некоторые предположения мы Выбираем для проверки их совместимости со статистическим материалом и называем такие предположения статистическими гипотезами. НиЖе Мы расскажем, как осуществляется проверка статистических гипотез.
Что такое ранг в статистике
Уважаемые посетители Портала Знаний, если Вы найдете ошибку в тексте, выделите, пожалуйста, ее мышью и нажмите Сtrl+Enter. Мы обязательно исправим текст!
Средний ранг
Пусть имеется выборка из n наблюдений 


Средний ранг 



Пример. Ранжируем выборку из пяти наблюдений (11,12,14,14,14). Значение «14» встречается в ней 3 раза. Если бы равные наблюдения мы считали различными, то набор рангов для этой выборки был бы (1,2,3,4,5). Поскольку все значения «14» равноправны, присваиваем им усреднённый ранг (3+4+5)/3=4 и получаем набор рангов (1,2,4,4,4).
Синоним: midrank – средний ранг, срединный ранг.
СОДЕРЖАНИЕ
Стратегии присвоения рейтингов
Стандартный конкурсный рейтинг (рейтинг «1224»)
В соревновательном рейтинге элементы, которые сравниваются с равными, получают один и тот же ранговый номер, а затем в ранжируемых числах остается пробел. Количество номеров ранжирования, оставленных в этом промежутке, на единицу меньше, чем количество сравниваемых элементов, равных. Эквивалентно, номер ранжирования каждого элемента равен 1 плюс количество элементов, ранжированных выше него. Эта стратегия ранжирования часто применяется для соревнований, так как это означает, что если два (или более) участника занимают одинаковую позицию в рейтинге, положение всех тех, кто занимает место ниже, не изменяется (т. Е. Участник занимает второе место только в том случае, если ровно один человек набирает больше, чем они, третье, если ровно два человека набирают больше, чем они, четвертое, если ровно три человека набирают больше, чем они, и т. д.).
Таким образом, если A занимает место впереди B и C (которые сравниваются одинаково), которые оба занимают место выше D, тогда A получает рейтинг номер 1 («первый»), B получает рейтинг номер 2 («совместный второй»), C также получает рейтинг номер 2 («совместный второй») и D получает рейтинг 4 («четвертый»).
Модифицированный рейтинг конкурса (рейтинг «1334»)
Таким образом, если A занимает место впереди B и C (которые сравниваются одинаково), которые оба занимают первое место в D, тогда A получает рейтинг номер 1 («первый»), B получает рейтинг номер 3 («совместная третья»), C также получает рейтинг номер 3 («совместный третий») и D получает рейтинг 4 («четвертый»). В этом случае никто не получит рейтинг 2 («второй»), и это останется как пробел.
Плотный рейтинг (рейтинг «1223»)
При плотном ранжировании элементы, которые сравниваются в равной степени, получают один и тот же ранговый номер, а следующие элементы получают следующий за ним ранговый номер. Эквивалентно, номер ранжирования каждого элемента равен 1 плюс количество элементов, ранжированных выше него, которые различаются по порядку ранжирования.
Таким образом, если A занимает место впереди B и C (которые сравниваются одинаково), которые оба занимают место выше D, тогда A получает рейтинг номер 1 («первый»), B получает рейтинг номер 2 («совместный второй»), C также получает рейтинг номер 2 («совместный второй») и D получает рейтинг 3 («третий»).
Порядковый рейтинг (рейтинг «1234»)
При порядковом ранжировании все элементы получают различные порядковые номера, включая элементы, которые сравниваются одинаково. Присвоение различных порядковых номеров элементам, которые сравниваются одинаково, может выполняться случайным образом или произвольно, но обычно предпочтительнее использовать произвольную, но последовательную систему, поскольку это дает стабильные результаты, если ранжирование выполняется несколько раз. Примером произвольной, но последовательной системы может быть включение других атрибутов в порядок ранжирования (таких как алфавитный порядок имени участника), чтобы гарантировать, что никакие два элемента не совпадают в точности.
С этой стратегией, если A занимает место впереди B и C (которые сравнивают равные), которые оба занимают место выше D, тогда A получает рейтинг номер 1 («первый»), а D получает рейтинг номер 4 («четвертый»), и либо B получает ранжирующий номер 2 («второй»), а C получает ранжирующий номер 3 («третий»), или C получает ранжирующий номер 2 («второй»), а B получает ранжирующий номер 3 («третий»).
При компьютерной обработке данных порядковое ранжирование также называется «нумерацией строк».
Дробное ранжирование (рейтинг «1 2,5 2,5 4»)
Элементы, которые сравнивают равные, получают одинаковый номер ранжирования, который является средним значением того, что они имели бы в порядковом рейтинге; эквивалентно, номер ранжирования, равный 1, плюс количество элементов, ранжированных выше, плюс половина количества элементов, равных ему. Эта стратегия обладает тем свойством, что сумма номеров ранжирования такая же, как и при порядковом ранжировании. По этой причине он используется при вычислении количества Борда и в статистических тестах (см. Ниже).
Таким образом, если A опережает B и C (которые в сравнении равны), которые оба занимают место впереди D, то A получает рейтинг 1 («первый»), B и C получают каждый рейтинг 2,5 (среднее значение «совместное второе / третье место»). «) и D получает рейтинг 4 (» четвертый «).
Вот пример: Предположим, у вас есть набор данных 1.0, 1.0, 2.0, 3.0, 3.0, 4.0, 5.0, 5.0, 5.0.
Порядковые ранги: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Таким образом, дробные ранги следующие: 1.5, 1.5, 3.0, 4.5, 4.5, 6.0, 8.0, 8.0, 8.0.
Рейтинг в статистике
Некоторые виды статистических тестов используют расчеты на основе рангов. Примеры включают:
Некоторые ранги могут иметь нецелые значения для связанных значений данных. Например, когда имеется четное количество копий одного и того же значения данных, вышеописанный дробный статистический ранг связанных данных заканчивается на 1/2.
Функция ранжирования в Excel
Сравнение рейтингов
Рейтинг и социально-экономическая оценка
Методология ранжирования, основанная на некоторых конкретных индексах, является одной из наиболее распространенных систем, используемых политиками и международными организациями для оценки социально-экономического контекста стран. Вот несколько ярких примеров: Индекс человеческого развития (ООН), Индекс ведения бизнеса (Всемирный банк), Индекс восприятия коррупции (Transparency International) и Индекс экономической свободы (Фонд наследия). Например, Индикатор «Ведение бизнеса» Всемирного банка измеряет правила ведения бизнеса и их соблюдение в 190 странах. Страны ранжируются по 10 показателям, которые синтезируются для получения окончательного рейтинга. Каждый индикатор состоит из подиндикаторов; например, индикатор регистрации собственности состоит из 4 субпоказателей, измеряющих время, процедуры, затраты и качество системы регистрации земли. Очевидно, что такие ранги основаны на субъективных критериях присвоения баллов. Иногда принятые параметры могут приводить к несоответствиям с эмпирическими наблюдениями, поэтому при применении этих критериев могут возникнуть потенциальные ошибки и парадокс.
Рейтинг как социальная игра
Что такое ранг в статистике. Ранговые коэффициенты связи
Рангом элемента выборки называется порядковый номер этого элемента в вариационном ряду или, другими словами, число элементов выборки меньших или равных
Следовательно, выборочному значению соответствует порядковая статистика вариационного ряда.
Ранговым вектором выборки называется перестановка чисел 1, 2, которая получается при замене элементов выборки их рангами. Ранговой статистикой называется произвольная функция от рангового вектора. Ранговый алгоритм предписывает сравнение некоторой ранговой статистики с порогом.
Исходную выборку можно восстановить, если известен вектор порядковых статистик и ранговый вектор R. Отдельно любой из этих двух векторов представляет необратимое нелинейное преобразование исходной выборки. Для однородной независимой выборки случайные векторы и R независимы.
Ранг элемента выборки размером при помощи функции единичного скачка или знаковой функции можно представить следующим образом:

Из (13.168 a и б) следует, что ранги являются знаковыми статистиками от разностей выборочных значений.
где область включает те точки выборочного пространства, которым при упорядочивании соответствует заданный вектор

Отметим, что ранговый вектор однородной независимой выборки инвариантен к безынерционному преобразованию выборки
Суммарный ранг важности а i
Среднее значение для суммарных рангов рассматриваемого ряда
Суммарное квадратическое отклонение Sсуммарных событий от среднего значения а есть
называемое коэффициентом конкордации. Величина Wизменяется в пределах от 0 до 1. При W = 0 согласованности совершенно нет, т.е. связь между оценками различных экспертов отсутствует. Наоборот, при W = 1 согласованность мнений экспертов полная.
В том случае, если последовательность (5.2) кроме строгих неравенств имеет равенства, т.е. существует совпадение рангов, то формула для вычисления коэффициента конкордации имеет вид
Когда ранги повторяются, то для получения нормальной ранжировки, имеющей среднее значение ранга, равное
необходимо приписать событиям, имеющим одинаковые ранги, ранг, равный среднему значению мест, которые эти события поделили между собой.
Например, получена следующая ранжировка событий:
События 2 и 5 поделили между собой второе и третье места. Значит, им приписывается ранг
события 3, 4 и 6 поделили между собой четвертое, пятое, шестое места, и им приписывается ранг
Таким образом, получаем нормальную ранжировку:
Пример. Рассмотрим ранжированиеm= 10 событий р = 3 экспертами;N,Q,R. Результаты расчетов представлены в табл. 5.3.
Для крайних значений коэффициента конкордации могут быть высказаны следующие предположения. Если W= 0, то согласованности в оценках нет, поэтому для получения достоверных оценок следует уточнить исходные данные о событиях и (либо) изменить состав группы экспертов. При W = 1 далеко не всегда можно считать полученные оценки объективными, поскольку иногда оказывается, что все члены экспертной группы заранее сговорились, защищая свои общие интересы.
Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.
Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная : r ху = + 0,99, р > 99,9%).
на применение рангового метода
Задание: методом рангов установить направление и силу связи между стажем работы в годах и частотой травм, если получены следующие данные:
| Стаж работы в годах | Число травм | Порядковые номера (ранги) | Разность рангов | Квадрат разности рангов | |
| X | Y | d(х-у) | d 2 | ||
| До 1 года | 24 | 1 | 5 | -4 | 16 |
| 1-2 | 16 | 2 | 4 | -2 | 4 |
| 3-4 | 12 | 3 | 2,5 | +0,5 | 0,25 |
| 5-6 | 12 | 4 | 2,5 | +1,5 | 2,25 |
| 7 и более | 6 | 5 | 1 | +4 | 16 |
| Σ d 2 = 38,5 | |||||
Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каминскому)
где d – разность рангов х и у ;
Коэффициент ρ может принимать значения от 0 до ±1. Следует иметь в виду, что, поскольку коэффициент Спирмэна учитывает разность только рангов, а не самих значений х и у, он менее точен по сравнению с линейным коэффициентом. Поэто-му его крайние значения (1 или 0) нельзя безоговорочно расцени-вать как свидетельство функциональной связи или полного от-сутствия зависимости между х и у. Во всех других случаях, т.е. когда ρ не принимает крайних зна-чений, он довольно близок к r.
Формула (147) применима строго теоретически только тогда, когда отдельные значения х (и у), а следовательно, и их ранги не повторяются. Для случая повторяющихся (связанных) рангов есть другая, более сложная формула, скорректированная на число по-вторяющихся рангов. Однако опыт показывает, что результаты расчетов по скорректированной формуле для связанных рангов мало отличаются от результатов, полученных по формуле для не-повторяющихся рангов. Поэтому на практике формула (147) ус-пешно применяется как для неповторяющихся, так и для повто-ряющихся рангов.



где S – фактическая общая сумма баллов при оценке +1 каж-дой пары рангов с одинаковым порядком изменения и –1 каждой пары рангов с обратным порядком изме-нения;

Отметим, что случаи следования одинаковых повторяющихся рангов (в любом ряду) оцениваются баллом 0, т.е. они не учиты-ваются при расчете ни со знаком «+», ни со знаком «–».
Преимущества ранговых коэффициентов корреля-ции Спирмэна и Кендэла: они легко вычисляются, с их помощью можно изучать и измерять связь не только между количественны-ми, но и между качественными (описательными) признаками, ранжированными определенным образом. Кроме того, при ис-пользовании ранговых коэффициентов корреляции не требуется знать форму связи изучаемых явлений.
Если число ранжируемых признаков (факторов) больше двух, то для измерения тесноты связи между ними можно использовать предложенный М. Кендэлом и Б. Смитом коэффициент конкордации (множественный коэффициент ранговой корреляции):

Формула (150) применяется для случая, кода ранги по каж-дому признаку не повторяются. Если же есть связанные ран-ги, то коэффициент конкордации рассчитывается с учетом числа таких повторяющихся (связанных) рангов по каждому фактору:

где t – число одинаковых рангов по каждому признаку.
Коэффициент конкордации W может принимать значения от 0 до 1. Однако, необходимо проверить его на существенность (значимость) с помощью критерия χ2 при отсутствии связанных рангов по формуле (152), а при их наличии – по формуле (153):


Фактическое значение χ2 сравнивается с табличным, соответ-ствующим принятому уровню значимости α (0,05 или 0,01) и числу степеней свободы v = п – 1. Если χ2факт > χ2табл, то W – существенен (значим).
При выставлении экспертных оценок или в других случаях ранжирования возникают ситуации, когда двум или большему числу качеств приписываются одинаковые ранги. В этом случае правила ранжирования таковы:
1. Наименьшему числовому значению приписывается ранг 1.
2. Наибольшему числовому значению приписывается ранг, равный количеству ранжируемых величин.
3. В случае если несколько исходных числовых значений оказались равными, то им приписывается ранг, равный средней величине тех рангов, которые эти величины получили бы, если бы они стояли по порядку друг за другом и не были бы равны.
Отметим, что под этот случай могут попасть как первые, так и последние величины исходного ряда для ранжирования.
4. Общая сумма реальных рангов должна совпадать с расчетной, определяемой по формуле (1).
Например, психолог получил у 11 испытуемых следующие значения показателя невербального интеллекта: 113, 107, 123, 122, 117, 117, 105, 108, 114, 102, 104. Необходимо проранжировать эти показатели.
| № испытуемых п/п | Показатели интеллекта | Условные ранги | Ранги |
| (8) | 8,5 | ||
| (9) | 8,5 |
Проверим правильность ранжирования по формуле (1):
Просуммируем реальные ранги: 6+4+11+10+8,5+8,5+3+5+7+1+2=66.
Т.к. суммы совпали, то ранжирование выполнено верно.
В ранговой шкале применяется множество статистических методов. Наиболее часто к измерениям, полученным в этой шкале применяются коэффициенты корреляции Спирмена и Кэндалла, кроме того, применительно к данным, полученным в этой шкале, используют разнообразные критерии различий.
Так, в психологии часто используется семантический дифференциал Ч.Осгуда, который является примером измерения по интервальной шкале различных психологических особенностей личности, социальных установок, ценностных ориентации, субъективно-личностного смысла, различных аспектов самооценки.
Абсолютно Не знаю Совершенно
не согласен (не уверен) согласен
Однако, как подчеркивают С. Стивенс и ряд других исследователей, психологические измерения в шкале интервалов по сущности нередко оказываются измерениями, выполненными в шкале порядков. Основанием для этого утверждения служит тот факт, что функциональные возможности человека меняются в зависимости от разных условий. При измерении, например, силы с помощью динамометра или устойчивости внимания с помощью секундомера, результаты измерения в начале и в конце опыта по причине усталости испытуемого не будут квантифицироваться равными интервалами.
Только измерение по строго стандартизированной тестовой методике, при условии того, что распределение значений в репрезентативной (см. ниже) выборке достаточно близко к нормальному (см. ниже), может считаться измерением в интервальной шкале. Примером последнего могут служить стандартизованные тесты интеллекта, где условная единица измерения IQ эквивалентна как при низких, так и при высоких значениях интеллекта
Принципиально важным является и то, что к экспериментальным данным, полученным в этой шкале, применимо достаточно большое число статистических методов.
Шкалу отношений называют также шкалой равных отношений. Особенностью этой шкалы является наличие твердо фиксированного нуля, который означает полное отсутствие какого-либо свойства или признака. Шакала отношений является наиболее информативной шкалой, допускающей любые математические операции и использование разнообразных статистических методов.
Шкала отношений по сути очень близка интервальной, поскольку если строго фиксировать начало отсчета, то любая интервальная шкала превращается в шкалу отношений.
Именно в шкале отношений производятся точные и сверхточные измерения в таких науках, как физика, химия, микробиология. Измерение по шкале отношений производятся и в близких к психологии науках, таких, как психофизика, психофизиология, психогенетика.