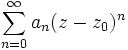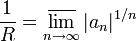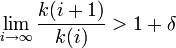что такое радиус сходимости

СОДЕРЖАНИЕ

Определение

Для степенного ряда f, определяемого как:

Некоторые могут предпочесть альтернативное определение, поскольку существование очевидно:

Нахождение радиуса сходимости

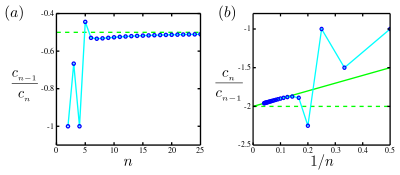
Возникают два случая. Первый случай теоретический: когда вы знаете все коэффициенты, вы берете определенные пределы и находите точный радиус сходимости. Второй случай практичен: когда вы строите решение сложной задачи в виде степенного ряда, вы, как правило, будете знать только конечное число членов в степенном ряду, от пары до ста членов. Во втором случае экстраполяция графика позволяет оценить радиус сходимости. c п <\ displaystyle c_ >

Теоретический радиус

Радиус сходимости можно найти, применив критерий корня к членам ряда. Корневой тест использует число

Предел, связанный с проверкой отношения, обычно легче вычислить, и когда этот предел существует, он показывает, что радиус сходимости конечен.

Это показано следующим образом. Тест отношения говорит, что ряд сходится, если

Практическая оценка радиуса в случае реальных коэффициентов

Радиус сходимости в комплексном анализе

Степенный ряд с положительным радиусом сходимости может быть преобразован в голоморфную функцию, если принять его аргумент как комплексную переменную. Радиус сходимости можно охарактеризовать следующей теоремой:

Радиус сходимости степенного ряда f с центром в точке a равен расстоянию от a до ближайшей точки, где f не может быть определено таким образом, чтобы сделать его голоморфным.

не имеет особенностей на действительной прямой, так как не имеет реальных корней. Его ряд Тейлора около 0 определяется выражением 1 + z 2 <\ displaystyle 1 + z ^ <2>>

Простой пример

Функция арктангенса тригонометрии может быть расширена в степенной ряд:

В этом случае легко применить корневой тест, чтобы найти, что радиус сходимости равен 1.

Более сложный пример

Рассмотрим этот степенной ряд:

напоминая, что если z = x + iy и e iy = cos ( y ) + i sin ( y ), то

Сходимость на границе

имеет радиус сходимости 1 и расходится в каждой точке границы.

Пример 3: степенной ряд

Пример 4: степенной ряд

Скорость сходимости

Если мы расширим функцию

Таким образом, для этих конкретных значений самая быстрая сходимость разложения степенного ряда находится в центре, и по мере удаления от центра сходимости скорость сходимости замедляется до тех пор, пока вы не достигнете границы (если она существует) и не пересечетесь, в в этом случае серии разойдутся.

Абсцисса сходимости ряда Дирихле.

Такой ряд сходится, если действительная часть s больше определенного числа в зависимости от коэффициентов a _n : абсцисс сходимости.

Источник

Радиус сходимости

Круг сходимости степенного ряда

Радиус сходимости

Радиус круга сходимости называется радиусом сходимости ряда.

Радиус сходимости ряда Тейлора аналитической функции равен расстоянию от центра ряда до множества особых точек функции, и может быть вычислен по формуле Коши — Адамара:

Эта формула выводится на основе признака Коши.

Теорема Адамара

Для степенного ряда

,

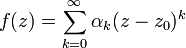
у которого почти все коэффициенты равны нулю, в том смысле, что последовательность ненулевых коэффициентов a_k(i) удовлетворяет

См. также

Полезное

Смотреть что такое «Радиус сходимости» в других словарях:

Радиус сходимости — радиус круга сходимости степенного ряда (см. Круг сходимости), т. е. такое число r, что степенной ряд z| г … Большая советская энциклопедия

КРУГ СХОДИМОСТИ — степенного ряда круг вида в к ром ряд (1) абсолютно сходится, а вне его, при расходится. Иными словами, К. с. есть внутренность множества точек сходимости ряда (1). Радиус RК. с. наз. радиусом сходимости ряда (1). К. с. может вырождаться в точку… … Математическая энциклопедия

предел сходимости — радиус сходимости — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы радиус сходимости EN convergence limit … Справочник технического переводчика

СТЕПЕННОЙ РЯД — 1)С. р. по одному комплексному переменному z функциональный ряд вида где a центр ряда, bk его коэффициенты, bk(z a)k члены ряда. Существует число r, называемое радиусом сходимости С. р. (1) и определяемое по формуле Коши Адамара такое, что при |z … Математическая энциклопедия

ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия

Источник

Радиус схождения: определение, примеры и решаемые упражнения

Содержание:

Любая аналитическая функция f (z) связал ряд степеней вокруг неособой точки, называемой Серия Тейлора:

кудак центр круга сходимости, z независимая переменная функции и c_п— коэффициенты, связанные с производными функции F по делу г = а.

Радиус сходимости р положительное действительное число, определяющее регион:

Чтобы определить область, в которой ряд сходится, мы вычисляем частное между членом (nth + 1) и членом (nth):

Абсолютное значение указанного выше частного составляет | x | и его предел, когда п → ∞ это также | x |.

Для сходимости рядов необходимо, чтобы:

Тогда радиус сходимости этого ряда равен г = 1, поскольку он сходится для значений x, которые находятся на расстоянии меньше 1 по отношению к центру х = 0.

Пример 2

Мы хотим найти ряд Тейлора функции е (х) = 1 / (1 + х) вокруг точки х = 0 и определить его радиус сходимости.

Чтобы найти ряд, мы берем последовательные производные функции f (x), из которых мы покажем первые три:

Принимая во внимание, что член нулевого порядка ряда Тейлора равен:

Первый заказ:f ‘(0) / 1!

И так далее, мы имеем, что ряд Тейлора данной функции:

Что совпадает со степенным рядом, изученным в примере 1.

Этот результат полностью совпадает с полученным в примере 1 другим способом.

Тот факт, что зона сходимости ряда Тейлора является открытым интервалом (-1, 1), означает, что функция и ряд совпадают в этом интервале, но не вне его.

Это показано на рисунке 2, где 41 член был взят из ряда Тейлора, нарисованный сплошной синей линией, в то время как исходная функция показана красной сегментной линией.

Решенные упражнения

— Упражнение 1

Рассмотрим ту же функцию е (х) = 1 / (1 + х) из примера 2, но на этот раз нас просят найти ряд Тейлора указанной функции вокруг точки a = 1.

Решение

Мы находим последовательные члены-коэффициенты ряда, начиная с независимого члена, который равен f (1) = ½.

Следующий коэффициент, соответствующий члену первого порядка, равен:

Далее следует коэффициент третьего порядка:

И так далее. Сериал Тейлора будет:

— Упражнение 2.

Найдите радиус сходимости предыдущего ряда

Решение

Запишем n-й член и n-й член плюс один:

Мы вычисляем частное этих двух членов, которое показано ниже в упрощенной форме:

За абсолютное значение предыдущего выражения берется получение:

Однако для сходимости ряда необходимо, чтобы предыдущая величина была строго меньше единицы, то есть:

Черные металлы: структура, виды, характеристики

Страх одиночества: как преодолеть его за 12 практических шагов

Источник

Степенные ряды

Радиус и круг сходимости степенного ряда.

Функциональные ряды вида
$$
\sum_^<\infty>c_(\zeta — a)^,\label
$$
где \(c_\ (n = 1, 2, \ldots)\) и \(a\) — заданные комплексные числа, \(\zeta\) — комплексное переменное, называют степенными рядами, а числа \(c_\) — коэффициентами степенного ряда \eqref.

Полагая в \eqref \(z = \zeta — a\), получим ряд
$$
\sum_^<\infty>c_z^,\label
$$
исследование сходимости которого эквивалентно исследованию сходимости ряда \eqref.

Если степенной ряд \eqref сходится при \(z = z_ <0>\neq 0\), то он сходится, и притом абсолютно, при любом \(z\) таком, что \(|z| |z_<1>|\).

Так как ряд \eqref сходится в точке \(z_<0>\), то должно выполняться условие
$$
\lim_c_z_<0>^ = 0,\nonumber
$$
откуда следует ограниченность последовательности \(\z_<0>^\>\), то есть
$$
\exists M > 0: \forall n \in \mathbb \rightarrow |c_z_<0>^| \leq M.\label
$$
Используя неравенства \eqref и \eqref, получаем
$$
|c_z^| = |c_z_<0>^|\left|\frac>\right|^ \leq M q^,\ \mbox<где>\ 0 \leq q Следствие 1.

Если ряд \eqref сходится в точке \(z_ <0>\neq 0\), то в круге \(K_ <1>= \

Если ряд \eqref сходится в точке \(z_ <0>\neq 0\), то ряды
$$
\sum_^<\infty>c_z^,\quad m \in \mathbb,\label
$$
$$
\sum_^<\infty>nc_z^\label
$$
сходятся абсолютно в круге \(K_<0>\), а в круге \(K_<1>\) — абсолютно и равномерно.

\(\circ\) Для ряда \eqref в круге \(K_<0>\) выполняется неравенство
$$
|c_z^| \leq \frac<|z_<0>|^>q^,\ 0 \leq q 0\), \(B > 0\), \(0 \leq q Теорема 2.

Для всякого степенного ряда \eqref существует \(R\) (\(R \geq 0\) — число или \(+\infty\)) такое, что:

\(\circ\) Пусть \(D\) — множество всех точек сходимости ряда \eqref. Это непустое множество, так как в точке \(z = 0\) ряд \eqref сходится.

Если \(D\) — неограниченное множество, то ряд \eqref сходится в произвольной точке \(\tilde\) комплексной плоскости. В самом деле, возьмем точку \(z_ <0>\in D\) такую, что \(|\tilde| R\). Тогда \(z’ \in D\) (по определению точной верхней грани), и поэтому ряд \eqref расходится в точке \(z’\). \(\bullet\)

На границе круга \(K\) ряд \eqref может как сходиться, так и расходиться. В любом меньшем круге \(K_ <1>= \

Если \(R\) — радиус сходимости степенного ряда \eqref, причем \(0 Доказательство.

\(\circ\) Теорема приводится без доказательства. \(\bullet\)

Если существует конечный или бесконечный \(\displaystyle\lim_ \sqrt[n]<|c_|>\), то для радиуса \(R\) сходимости ряда \eqref справедлива формула
$$
\frac<1> = \lim_ \sqrt[n]<|c_|>,\label
$$
а если существует конечный или бесконечный \(\displaystyle\lim_ \left|\frac>>\right|\), то
$$
R = \lim_ \left|\frac>>\right|,\label
$$

\(\circ\) Докажем формулу \eqref. Обозначим \(\rho = \displaystyle\lim_ \sqrt[n]<|c_|>\).

Пределы \eqref и \eqref могут не существовать. Однако имеется универсальная формула для вычисления радиуса сходимости \(R\) степенного ряда \eqref, а именно формула
$$
\frac<1> = \overline<\lim_> \sqrt[n]<|c_|>,\label
$$
которую называют формулой Коши-Адамара.

Найти радиус сходимости \(R\) степенного ряда \(\displaystyle\sum_^<\infty>c_z^\),

Найти радиус сходимости \(R\) степенного ряда \(\displaystyle\sum_^<\infty>2^z^<5n>\).

\(\vartriangle\) Обозначим \(2z^ <5>= t\). Тогда \(\displaystyle\sum_^<\infty>2^z^ <5n>= \sum_^<\infty>t^\), причем ряд \(\sum_^<\infty>t^\) сходится, если \(|t| 1\). Поэтому ряд \(\displaystyle\sum_^<\infty>2^z^<5n>\) сходится, если \(2|z|^ <5>\displaystyle\frac<1><\sqrt[5]<2>>\). Итак, радиус сходимости \(R = \displaystyle\frac<1><\sqrt[5]<2>>\). Тот же результат следует из формулы \eqref, так как
$$
\overline<\lim_> \sqrt[n]<|c_|> = \lim_ \sqrt[5n]<2^> = \sqrt[5]<2>.\ \blacktriangle\nonumber
$$

Для степенного ряда \(\displaystyle\sum_^<\infty>c_(z — a)^\) круг сходимости \(K\) имеет вид \(K = \ — R, x_ <0>+ R)\) называют интервалом сходимости, a \(R\) — радиусом сходимости ряда \eqref. Радиус сходимости ряда \eqref совпадает с радиусом сходимости ряда \(\displaystyle\sum_^<\infty>a_(z — x_<0>)^\), где \(z\) — комплексное переменное. При \(R = 0\) ряд \eqref сходится лишь в точке \(x = x_<0>\), а при \(R = +\infty\) — на всей числовой прямой.

Регулярные функции.

Введем понятие функции комплексного переменного. Пусть каждой точке \(z \in E\), где \(E\) — множество точек комплексной плоскости, поставлено в соответствие комплексное число \(w\). Тогда говорят, что на множестве \(E\) определена функция комплексного переменного, и пишут \(w = f(z)\), где символом \(f\) обозначено правило (закон), определяющее это соответствие.

Понятия предела, непрерывности, производной для функции комплексного переменного вводятся по аналогии с соответствующими понятиями для функции действительного переменного. Если
$$
\forall \varepsilon > 0\ \exists \delta = \delta_ <\varepsilon>> 0: \forall z: |z — a| Определение.

Функция комплексного переменного \(f(z)\) называется регулярной (однозначной аналитической, голоморфной) в точке \(a\), если она определена в некоторой окрестности точки \(a\) и представима в некотором круге \(|z — a| 0\), сходящимся к \(f(z)\) степенным рядом
$$
f(z) = \sum_^<\infty>c_(z — a)^.\label
$$

Отметим, что любой многочлен, то есть функция вида \(P(z) = \displaystyle\sum_^<\infty>a_z^\), является регулярной функцией в каждой точке комплексной плоскости.

Рациональная функция \(f(z) = \displaystyle\frac(z)>(z)>\), где \(P_\) и \(Q_\) — многочлены степени \(n\) и \(m\) соответственно, регулярна в каждой точке \(a\), в которой \(Q_ \neq 0\). Если многочлены \(P_\) и \(Q_\) не имеют общих корней и если \(z = z_<0>\) — корень многочлена \(Q_(z)\), то \(\displaystyle\lim_>f(z) = \infty\), а точку \(z_<0>\) называют полюсом функции \(f(z)\). Полюсы — один из типов особых точек функций комплексного переменного.

В теории функций комплексного переменного доказывается, что на границе круга сходимости степенного ряда \(\displaystyle\sum_^<\infty>c_(z — a)^\) лежит хотя бы одна особая точка его суммы \(f(z)\) и что радиус сходимости этого ряда равен расстоянию от точки \(a\) до ближайшей к \(a\) особой точки функции \(f(z)\).

В частности, если \(f(z) = \displaystyle\frac(z)>(z)>\), причем многочлены \(P_\) и \(Q_\) не имеют общих корней, то радиус сходимости \(R\) степенного ряда \(\displaystyle\sum_^<\infty>c_(z — a)^\) равен расстоянию от точки \(a\) до ближайшего к этой точке корня многочлена \(Q_(z)\), то есть
$$
R = \min_ <1 \leq k m>|z_ — a|,\nonumber
$$
где \(z_ (k = \overline<1, m>)\) — корни многочлена \(Q_(z)\) (предполагается, что \(a \neq z_\), \(k = \overline<1, m>\)).

Функция \(f(z)\), регулярная в точке \(a\), единственным образом представляется рядом \eqref.

\(\circ\) Пусть функция \(f(z)\) имеет два представления в виде степенного ряда \eqref в круге \(K = \ $$
f(z) = \sum_^<\infty>c_(z — a)^ = \sum_^<\infty>\tilde_(z — a)^.\label
$$
Докажем, что \(c_ = \tilde_\) для \(n = 0, 1, 2, …\)

По условию ряды \(\displaystyle\sum_^<\infty>c_(z — a)^\) и \(\displaystyle\sum_^<\infty>\tilde_(z — a)^\) сходятся в круге \(K\), и поэтому (см. следствие 1 из теоремы 1) эти ряды сходятся равномерно в круге \(K_ <1>= \

Свойства степенных рядов.

\(\circ\) Пусть \(R\), \(R_<1>\) и \(R_<2>\) — радиусы сходимости рядов \eqref, \eqref и \eqref соответственно, \(K\), \(K_<1>\) и \(K_<2>\) — круги сходимости этих рядов. Докажем, что
$$
R_ <1>= R = R_<2>.\label
$$

Так как \(\displaystyle\frac<1> \leq 1 \leq n\) для любого \(n \in \mathbb\), то
$$
\left|\frac>z^\right| \leq |z| \cdot |c_z^| \leq |z|^ <2>\cdot |nc_z^|.\label
$$
Неравенства \eqref справедливы при любом \(n \in \mathbb\) и при любом \(z\).

\(\circ\) Рассмотрим ряд
$$
\sum_^ <\infty>k a_ (x — x_<0>)^.\label
$$
составленный из производных членов ряда \eqref. По теореме 6 ряд \eqref имеет тот же радиус сходимости, что и ряд \eqref, а по следствию 1 из теоремы 1 ряд \eqref сходится равномерно на отрезке \(\Delta_ <\rho>= [x_ <0>— \rho, x_ <0>+ \rho]\), где \(\rho\) — произвольное число такое, что \(0 Следствие.

Коэффициенты ряда \eqref, имеющего радиус сходимости \(R > 0\), выражаются формулами
$$
a_ <0>= f(x_<0>),\quad a_ = \frac(x_<0>)>,\quad n \in \mathbb.\label
$$

\(\circ\) Формулы \eqref получаются из равенств \eqref и \eqref при \(x = x_<0>\). \(\bullet\)

Из формул \eqref следует единственность разложения функции \(f(x)\) в степенной ряд вида \eqref.

Источник

Степенные ряды

Содержание

Определение [ править ]

Лемма Абеля [ править ]

Вся теория степенных рядов основана на лемме Абеля.

[math]|a_n x_1^n| = |a_n x_0^n| \left(\frac<|x_1|><|x_0|>\right)^n[/math]

[math]\sum\limits_^\infty q^n[/math] — сходится, поэтому, интересующий наш ряд мажорируется сходящимся числовым рядом, значит, он тоже сходится.[math]\triangleleft[/math]

Радиус сходимости [ править ]

Можно определить важнейшую для теории величину — радиус сходимости ряда.

1) [math]|x| \lt R[/math] [math]\Rightarrow[/math] ряд абсолютно сходится.

2) [math]\forall [a; b] \in (-R; R)[/math] ряд сходится абсолютно и равномерно.

3) [math]|x| \gt R[/math] [math]\Rightarrow[/math] ряд расходится.

4) [math]|x| = R[/math] — неопределённость.

2) [math]\exists \delta \gt 0 : [a; b] \subset [-\delta; \delta] \subset (-R; R)[/math]

3) Следствие определения радиуса сходимости.

4) Ну неопределённость [math]:)[/math][math]\triangleleft[/math]

Докажем первый пункт. Второй доказывается аналогично.

Рассмотрим [math]\sum\limits_^\infty |a_n x^n|[/math] и применим к нему признак Даламбера.

Итого: [math]|x| \lt q[/math] — ряд сходится, [math]|x| \gt q[/math] — ряд расходится.

Второй пункт доказывается аналогично радикальным признаком Коши.

Примеры [ править ]

Произведение степенных рядов [ править ]

По теореме о радиусе сходимости, на промежутке сходимости ряд сходится абсолютно. Если взять два степенных ряда, то на общей части их промежутка сходимости, ряды будут абсолютно сходиться, и, значит, с ними можно делать любые арифметические действия. В частности, их можно умножать по Коши:

[math]f(x) g(x) = \sum\limits_^\infty c_n x^n[/math]

Вывод: произведение двух степенных рядов по правилу Коши — степенной ряд с суммой, равной произведению сумм исходных рядов.

По теореме о радиусе сходимости, на любом отрезке из [math](-R; R)[/math] степенной ряд сходится равномерно.

Значит, по теоремам о почленном дифференцировании и интегрировании рядов, их можно дифференцировать и интегрировать, и опять будет получаться сходящийся степенной ряд.

Вопрос: «Каковы будут радиусы сходимости почленно проинегрированных или продифференцированных рядов?»

Ответ: «Почленное интегрирование или дифференцирование не меняет радиуса сходимости ряда».

Выясним, что для [math]f(x)[/math] и [math]f'(x)[/math] одинаковые радиусы сходимости.

Поэтому, промежуток сходимости продифференцированного ряда [math]\subset[/math] промежутку сходимости исходного ряда.

Источник