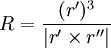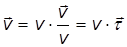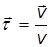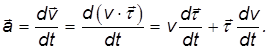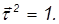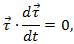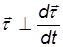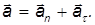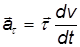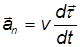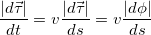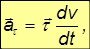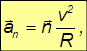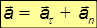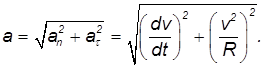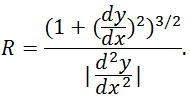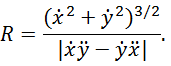что такое радиус кривизны траектории

Что такое радиус кривизны траектории?

Что такое радиус кривизны траектории точки?

В каком случае радиус кривизны траектории точки равен бесконечности?

При этом кривизна каждой дуги определяется её радиусом кривизны, направленном к дуге из мгновенного центра поворота, находящегося в той же плоскости, что и сама дуга. При том прямая линия рассматривается как предельный случай кривой, радиус кривизны которой может считаться равным бесконечности.

Что такое радиус кривизны формула?

Как найти радиус кривизны функции в точке?

Радиусом кривизны кривой в точке M(x,y) называется величина, обратная кривизне K данной кривой в рассматриваемой точке: R=1K. Следовательно, для плоских кривых, заданных явным уравнением y=f(x), радиус кривизны в точке M(x,y) будет определяться выражением R=[1+(y′(x))2]32|y′′(x)|.

Как найти уравнение траектории движения точки?

Для того чтобы получить уравнение траектории движения тела (y=y(x)) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) t и подставим его в выражение (3), получим: t=xv0cosα ; y=v0xv0cosα sinα −g2(xv0cosα )2→y=x tg α−

Что показывает кривизна траектории?

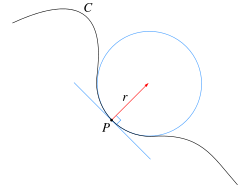
Кривизна траектории характеризует скорость поворота касательной при движении. Радиус кривизны траектории в данной точке – это радиус окружности, которая сливается на бесконечно малом участке в данном месте с кривой (рис. 1.8).

Почему изменяется радиус кривизны трека?

Радиус кривизны трека зависит от массы, скорости и заряда частицы. Радиус тем меньше (т е. отклонение частицы от прямолинейного движения больше), чем меньше масса и скорость частицы и чем больше ее заряд.

Что такое длина траектории?

Линию, по которой движется тело, называют траекторией движения тела. Длину траектории, по которой движется тело в течение некоторого промежутка времени, называют пройденным путём.

В каком случае касательное ускорение равно нулю?

Касательное ускорение равно нулю, если = d / dt = 0. Это условие выполняется, если все время v = | | = const, то есть при равномерном движении точки по траектории любой формы.

Как найти максимальный радиус кривизны?

Как найти кривизну?

Кривизну кривой можно определить как отношение угла поворота касательной Δφ к длине пройденной дуги Δs=MM1. Такое отношение ΔφΔs называется средней кривизной дуги кривой. Когда точка M1 приближается к точке M, мы получаем кривизну кривой в точке M: k=limΔs→0ΔφΔs=dφds.

Как обозначить радиус кривизны?

Как определить радиус кривизны трека?

Что такое кривизна линии?

Кривизна́ — собирательное название ряда характеристик (скалярных, векторных, тензорных), описывающих отклонение того или иного геометрического «объекта» (кривой, поверхности, риманова пространства и т. д.) от соответствующих «плоских» объектов (прямая, плоскость, евклидово пространство и т. д.).

Почему радиус кривизны на разных участках?

Радиусы кривизны разных участках трека одной и той же частицы различны, т. к. траектории заряженных частиц в магнитном поле направляются под действием силы Лоренца. Чем больше заряд частицы, тем меньше масса частицы и тем больше кривизна траектории.

Источник

Радиус кривизны

Радиус кривизны — величина, обратная кривизне. Радиус кривизны характеризует величину соответствия кривой от прямой. Чем больше радиус кривизны, тем больше кривая похожа на прямую.

Радиус кривизны определяется для конкретной точки конкретной кривой он равняется радиусу соприкасающейся окружности.

Вычисление

Пусть кривая задана параметрически, r(τ) Тогда радиус кривизны можно найти, воспользовавшись формулой:

Полезное

Смотреть что такое «Радиус кривизны» в других словарях:

радиус кривизны — Радиус дуги окружности, наиболее точно соответствующей форме закругления рассматриваемого элемента. [ГОСТ Р 41.61 2001] Тематики автотранспортная техника … Справочник технического переводчика

Радиус кривизны R_n — Радиус рабочей поверхности преобразователя Источник … Словарь-справочник терминов нормативно-технической документации

радиус кривизны — 2.8 радиус кривизны: Радиус дуги окружности, наиболее точно соответствующей форме закругления рассматриваемого элемента. Источник … Словарь-справочник терминов нормативно-технической документации

радиус кривизны — kreivumo spindulys statusas T sritis Standartizacija ir metrologija apibrėžtis Kreivės arba kreivo paviršiaus spindulys. atitikmenys: angl. radius of curvature vok. Krümmungsradius, m rus. радиус кривизны, m pranc. rayon de courbure, m … Penkiakalbis aiškinamasis metrologijos terminų žodynas

радиус кривизны — kreivumo spindulys statusas T sritis fizika atitikmenys: angl. radius of curvature vok. Krümmungsradius, m rus. радиус кривизны, m pranc. rayon de courbure, m … Fizikos terminų žodynas

Радиус кривизны — радиус круга кривизны (См. Кривизна) в данной точке кривой … Большая советская энциклопедия

Радиус кривизны — см. ст. Дифференциальное исчисление и ст. Кривизна … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Радиус кривизны мульды сдвижения — величина, обратная кривизне мульды сдвижения. Источник … Словарь-справочник терминов нормативно-технической документации

радиус кривизны беговой дорожки протектора — радиус кривизны беговой дорожки Радиус наружной поверхности беговой дорожки протектора в радиальной плоскости колеса. Rпр радиус кривизны беговой дорожки; С раствор бортов; Вб ширина борта покрышки. [ГОСТ 22374 77] Тематики шины пневматические… … Справочник технического переводчика

радиус кривизны линии притупления продольной кромки зуба — (Pk) радиус кривизны линии притупления [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины понятия, относящиеся к зубчатому колесупрофиль зуба Синонимы радиус кривизны линии притупления … Справочник технического переводчика

Источник

Что такое радиус кривизны траектории

4.1. Движение по окружности с постоянной скоростью.

Движение по окружности — простейший вид криволинейного движения.

4.1.1. Криволинейное движение — движение, траекторий которого является кривая линия.

Для движения по окружности с постоянной скоростью:

1) траектория движения — окружность;

2) вектор скорости направлен по касательной к окружности;

3) вектор скорости постоянно меняет свое направление;

4) за изменение направления скорости отвечает ускорение, называемое центростремительным (или нормальным) ускорением;

5) центростремительное ускорение меняет только направление вектора скорости, при этом модуль скорости остается неизменным;

6) центростремительное ускорение направлено к центру окружности, по которой происходит движение (центростремительное ускорение всегда перпендикулярно вектору скорости).

4.1.2. Период (T) — время одного полного оборота по окружности.

Это величина постоянная, так как длина окружности постоянная и скорость движения постоянна

4.1.3 Частота — число полных оборотов за 1 с.

По сути, частота отвечает на вопрос: как быстро вращается тело?

4.1.4. Линейная скорость — показывает, какой путь проходит тело за 1 с (это та же самая скорость, о которой говорилось в предыдущих темах)

где R — радиус окружности.

4.1.5. Угловая скорость показывает, на какой угол поворачивается тело за 1 с.

где — угол, на который повернулось тело за время

4.1.6. Центростремительное ускорение

Напомним, что центростремительное ускорение отвечает только за поворот вектора скорости. При этом, так как скорость постоянная величина, то значение ускорения тоже постоянно.

4.1.7. Закон изменения угла поворота

Это полный аналог закона движения при постоянной скорости :

Роль координаты x играет угол роль начальной координаты играет скорость — угловая скорость И с формулой следует работать так же, как ранее работали с формулой закона равномерного движения.

4.2. Движение по окружности с постоянным ускорением.

4.2.1. Тангенциальное ускорение

Центростремительное ускорение отвечает за изменение направления вектора скорости, но если еще меняется и модуль скорости, то необходимо ввести величину отвечающую за это — тангенциальное ускорение

Из вида формулы ясно, что — это обычное ускорение, о котором говорилось раньше. Если то справедливы формулы равноускоренного движения:

где S — путь, который проходит тело по окружности.

Итак, еще раз подчеркнем, отвечает за изменение модуля скорости.

4.2.2. Угловое ускорение

Мы ввели аналог скорости для движения по окружности — угловая скорость. Естественно будет ввести и аналог ускорения — угловое ускорение

Угловое ускорение связано с тангенциальным ускорением:

Из формулы видно, что если тангенциальное ускорение постоянно, то и угловое ускорение будет постоянно. Тогда можем записать:

Формула является полным аналогом закона равнопеременного движения, поэтому работать с этой формулой мы уже умеем.

4.2.3. Полное ускорение

Центростремительное (или нормальное) и тангенциальное ускорения не являются самостоятельными. На самом деле, это проекции полного ускорения на нормальную (направлена по радиусу окружности, то есть перпендикулярно скорости) и тангенциальную (направлена по касательной к окружности в сторону, куда направлен вектор скорости) оси. Поэтому

Нормальная и тангенциальные оси всегда перпендикулярны, следовательно, абсолютно всегда модуль полного ускорения можно найти по формуле:

4.4. Движение по криволинейной траектории.

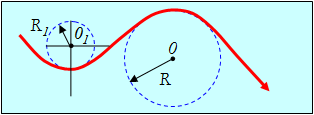
Движение по окружности является частным видом криволинейного движения. В общем случае, когда траектория представляет собой произвольную кривую (см. рис.), всю траекторию можно разбить на участки: AB и DE — прямолинейные участки, для которых справедливы все формулы движения по прямой; а для каждой участка, который нельзя рассмотреть как прямую, строим касательную окружность (окружность, которая касается траектории только в этой точке) — в точках C и D. Радиус касательной окружности называется радиусом кривизны. В каждой точке траектории радиус кривизны имеет свое значение.

Формула для нахождения радиуса кривизны :

где — нормальное ускорение в данной точке (проекция полного ускорения на ось, перпендикулярную вектору скорости).

Источник

Радиус кривизны плоской кривой

Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.

Между собой эти характеристики кривой связаны следующим образом:

k = 1/ρ (542.1)

Т.е. чем больше радиус кривой, тем меньше ее кривизна.

А теперь рассмотрим несколько частных случаев кривых.

Радиус кривизны окружности

Как определить радиус окружности, мы рассмотрим ниже.

Кривизна дуги

На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.

Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.

Понятие кривизны дуги формулируется так:

Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:

А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:

то, подставив значение длины дуги в уравнение (542.3), получим:

Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:

но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью

Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.

Рисунок 542.2. Дуга из точки начала координат.

Радиус кривизны прямой линии

Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.

Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:

k_п.л = 1/∞ = 0 (542.6)

все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими

Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:

1. Из уравнения (542.1) можно сделать вывод, что:

kp = 1 (542.7)

Соответственно для прямой линии:

0·∞ = 1 (542.7.2)

Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.

Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.

Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.

Радиус кривизны точки

k_т. = 1/0 = ∞ (542.9)

И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что «деление на ноль невозможно», тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.

Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.

Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.

R 2 = x 2 + y 2 (541.1.2)

А в общем случае, когда координаты центра окружности не совпадают с началом координат:

Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.

Плоские кривые с изменяющимся радиусом кривизны

Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:

1. Любую окружность можно рассматривать как некоторое множество дуг.

2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).

3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:

(542.3.1)

4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.

(542.11)

Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:

(542.12)

k = y» = d 2 y/dx 2 (542.12.2)

Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.

Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

2.6. Ускорение при криволинейном движении

Представим себе материальную точку, движущуюся по некоторой криволинейной траектории 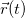. Запишем скорость в виде

и заметим, что вектор

— это единичный вектор, касательный к траектории и совпадающий по направлению с вектором скорости. Продифференцируем вектор скорости, записанный в данном представлении, и получим

Мы представили ускорение в виде двух слагаемых. Заметим прежде всего, что слагаемые ортогональны друг другу. Действительно, поскольку вектор 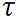— единичный, то

Дифференцируя это скалярное произведение, получаем

по свойству скалярного произведения.

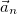
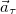
Таким образом, мы разложили ускорение на сумму двух взаимно ортогональных составляющих, обозначем их и :

Обсудим физический смысл каждого слагаемого. Слагаемое

— это тангенциальное ускорение, которое характеризует быстроту изменения модуля скорости. Эта часть полного ускорения 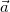направлена либо по скорости, когда производная dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное. Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:

направлено по нормали к траектории — перпендикулярно касательной к траектории и называется нормальным ускорением. Если тангенциальное ускорение определяет скорость, с которой меняется модуль вектора скорости, то нормальное ускорение определяет скорость, с которой меняется направление вектора скорости.

Рис. 2.10. К определению кривизны траектории

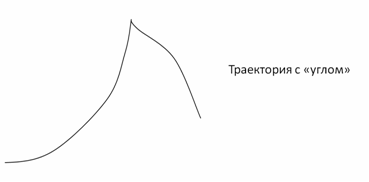
Рассмотрим «достаточно гладкую», в остальном произвольную плоскую криволинейную траекторию. Плоскую, то есть все точки траектории лежат в некоторой плоскости, — исключительно для упрощения выкладок, получаемый в рамках этого предположения, результат годится и для любой «достаточно гладкой» пространственной кривой, чьи точки уложить в одну плоскость невозможно. Последнее обстоятельство мы здесь рассматривать не будем, оно строго доказывается методами аналитической геометрии. Слова «достаточно гладкая» означают, что кривая описывается непрерывной функцией, имеющей непрерывные первую и вторую производные. С точки зрения физических приложений, требование существования непрерывных первых двух производных фактически не является ограничением на форму траектории, так как практически всегда выполнено. Проще говоря, на траектории не должно быть «углов» типа показанного на рисунке 2.11.

Такую «гладкую» кривую на любом её бесконечно малом участке можно заменить (рис. 2.12) участком окружности некоторого радиуса. Радиус этой окружности, аппроксимирующей траекторию на её бесконечно малом участке в окрестности некоторой точки, принято называть радиусом кривизны траектории в этой точке. Центр этой окружности принято называть центром кривизны траектории в данной точке. Кривизной траектории называется величина C = 1/R. Подчеркнем, что радиус кривизны, как и центр кривизны траектории — её локальные характеристика: каждой точке траектории соответствует свой радиус кривизны и свой центр кривизны. Исключениями являются: 1) окружность, её радиус кривизны во всех её точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой её конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.

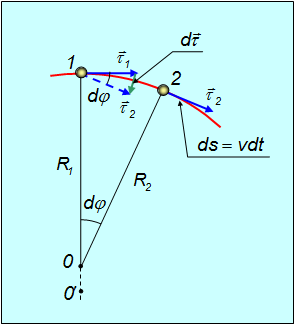
Рис. 2.12. К определению радиуса кривизны траектории

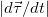
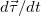
Вычислим модуль производной , входящей в выражение для нормального ускорения. Направлен вектор по нормали к траектории к центру к центру кривизны, что поясняет рис. 2.13.

Рис. 2.13. Графическое определение радиуса кривизны траектории

Для этого прежде всего перейдем от дифференцирования по времени к дифференцированию по «пути»: 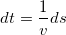, имеем:

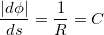
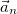
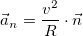
По определению производная кривизне кривой C, а величина ей обратная равна радиусу кривизны кривой R. Собирая всё вместе, для нормального ускорения окончательно получаем:

,

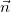
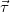
где нормаль перпендикулярна к касательной и всегда направлена к центру кривизны, см. рис. 11.

Приведем некоторое дополнительное пояснение к рисунку 11. Возьмем неподалеку от точки 1 точку 2. Построим в этих точках касательные единичные векторы ₁ и ₂. Перпендикуляры к этим касательным пересекутся в некоторой точке O₂. Заметим, что для кривой, не являющейся окружностью, расстояния R₁ и R₂ будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O₂ будет перемещаться вдоль прямой O₂1 и в пределе окажется в некоторой точке O₁. Расстояния R₁ и R₂ будут стремиться к общему пределу R, равному радиусу кривизны, а точка O₁ и будет центром кривизны для точки 1. Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту ₁). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.

Итак, в общем случае ускорение имеет две составляющие — тангенциальную

направленную вдоль касательной и определяющую скорость изменения модуля вектора скорости нормальную

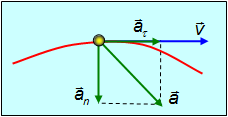
направленную перпендикулярно скорости к центру кривизны траектории и пропорциональную угловой скорости вращения вектора скорости при движении частицы вдоль криволинейной траектории (рис. 2.14).

Рис. 2.14. Тангенциальное и нормальное ускорения при ускоренном криволинейном движении.

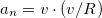
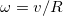
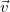
Действительно , где и есть угловая скорость вращения вектора скорости .

определяется по правилу параллелограмма. Модуль полного ускорения в соответствии с теоремой Пифагора равен

Выпишем без вывода формулы, связывающие радиус кривизны плоской траектории с координатами траектории. Если известна зависимость y = y(x), то

Если же траектория задана в параметрическом виде, x = x(t), y = y(t), то

Пример криволинейного движения с постоянным ускорением (тело, брошенное под углом к горизонту) приведен на следующем рисунке:

Рис. 2.15. Движение тела, брошенного под углом к горизонту

Источник