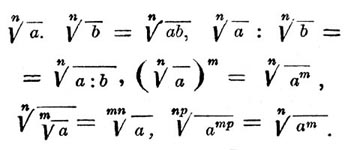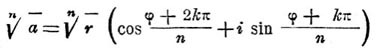что такое радикалы в математике

Радикал, в математике

Полезное

Смотреть что такое «Радикал, в математике» в других словарях:

РАДИКАЛ (в математике) — РАДИКАЛ, математический знак (измененное латинское r), которым обозначают действие извлечения корня, а также результат извлечения корня, т. е. число вида … Энциклопедический словарь

Радикал в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается Здесь а называется подкоренным числом, n показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

РАДИКАЛ — (лат., radix, radicis корень). 1) Политик, стремящийся к коренным преобразованиям в управлении страны. 2) английские социалисты носят также название радикалов. 3) В органической химии сложные вещества, способные соединяться с другими веществами… … Словарь иностранных слов русского языка

радикал — РАДИКАЛ, а, муж. 1. Сторонник радикализма (в 1 знач.), член радикальной партии. 2. Приверженец крайних, решительных действий, взглядов. | прил. радикалистский, ая, ое. II. РАДИКАЛ, а, муж. 1. В математике: знак, (Ц) обозначающий извлечение корня… … Толковый словарь Ожегова

РАДИКАЛ — (от лат. radicalis коренной) многозначный термин, используемый в разных науках (напр., в химии и математике) и практиках. 1, Сторонник радикальных (крайних, решительных) взглядов и действий, партий, движений. Бескомпромиссный человек. Склонность… … Большая психологическая энциклопедия

Радикал — В Викисловаре есть статья «радикал» Радикал (буквально: «коренной» от лат. radix … Википедия

РАДИКАЛ — Основное значение имеющий отношение к корню. Таким образом: 1. В математике знак (V), выражающий операцию разложения числа, стоящего под ним, на его корни. 2. В социальных/политических терминах описание любой точки зрения или предложения, в… … Толковый словарь по психологии

Центр (в математике) — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Вербицкий, Михаил Сергеевич — В Википедии есть статьи о других людях с такой фамилией, см. Вербицкий. Михаил Вербицкий … Википедия

Абель Нильс Хенрик — (Abel) (1802 1829), норвежский математик. Доказал, что алгебраические уравнения степени выше 4 й в общем случае неразрешимы в радикалах. Изучал интегралы от алгебраических функций (абелевы интегралы). Один из создателей теории эллиптических… … Энциклопедический словарь

Источник

Радикал в математике

Здесь а называется подкоренным числом, n — показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р. подразумевается число положительное. Алгебраическое выражение, содержащее Р., может подвергаться преобразованиям при помощи формул:

a = r (cos φ + i sin φ), где r > 0.

Для n значений Р. получается выражение

где k = 0, 1, 2. n— 1. В правой части

Полезное

Смотреть что такое «Радикал в математике» в других словарях:

РАДИКАЛ (в математике) — РАДИКАЛ, математический знак (измененное латинское r), которым обозначают действие извлечения корня, а также результат извлечения корня, т. е. число вида … Энциклопедический словарь

Радикал, в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается Здесь а называется подкоренным числом, n показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

РАДИКАЛ — (лат., radix, radicis корень). 1) Политик, стремящийся к коренным преобразованиям в управлении страны. 2) английские социалисты носят также название радикалов. 3) В органической химии сложные вещества, способные соединяться с другими веществами… … Словарь иностранных слов русского языка

радикал — РАДИКАЛ, а, муж. 1. Сторонник радикализма (в 1 знач.), член радикальной партии. 2. Приверженец крайних, решительных действий, взглядов. | прил. радикалистский, ая, ое. II. РАДИКАЛ, а, муж. 1. В математике: знак, (Ц) обозначающий извлечение корня… … Толковый словарь Ожегова

РАДИКАЛ — (от лат. radicalis коренной) многозначный термин, используемый в разных науках (напр., в химии и математике) и практиках. 1, Сторонник радикальных (крайних, решительных) взглядов и действий, партий, движений. Бескомпромиссный человек. Склонность… … Большая психологическая энциклопедия

Радикал — В Викисловаре есть статья «радикал» Радикал (буквально: «коренной» от лат. radix … Википедия

РАДИКАЛ — Основное значение имеющий отношение к корню. Таким образом: 1. В математике знак (V), выражающий операцию разложения числа, стоящего под ним, на его корни. 2. В социальных/политических терминах описание любой точки зрения или предложения, в… … Толковый словарь по психологии

Центр (в математике) — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Вербицкий, Михаил Сергеевич — В Википедии есть статьи о других людях с такой фамилией, см. Вербицкий. Михаил Вербицкий … Википедия

Абель Нильс Хенрик — (Abel) (1802 1829), норвежский математик. Доказал, что алгебраические уравнения степени выше 4 й в общем случае неразрешимы в радикалах. Изучал интегралы от алгебраических функций (абелевы интегралы). Один из создателей теории эллиптических… … Энциклопедический словарь

Источник

Математическая энциклопедия
РАДИКАЛЫ

Общая теория радикалов. Всюду в дальнейшем говорится только об алгебрах (имеются в виду алгебры над произвольным фиксированным ассоциативно-коммутативным кольцом с единицей); кольца являются частным случаем таких алгебр. Под идеалом алгебры, если это не оговорено специально, понимается двусторонний идеал.

(A) гомоморфный образ r-алгебры есть r-алгебра;

(Б) каждая алгебра Акласса обладает наибольшим r-идеалом, т. е. идеалом, содержащим любой r-идеал этой алгебры, и этот максимальный r-идеал наз. тогда r-радикалом этой алгебры и обозначается r(А).

Алгебра, совпадающая со своим Р., наз. радикальной. В любом классе алгебр и для любого радикала <0>является единственной одновременно радикальной и полупростой алгеброй. Подпрямое произведение любого множества полупростых алгебр само полупросто.

С каждым радикалом r связаны два подкласса алгебр в : класс (r) всех r-радикальных алгебр и класс (r) всех r-полупростых алгебр. По любому из этих классов однозначно находится радикал r(А).для каждой алгебры Аиз , а именно:

Алгебра r-радикальна тогда и только тогда, когда она не может быть отображена гомоморфно ни на одну ненулевую r-полупростую алгебру.

Известны условия на подклассы алгебр, необходимые и достаточные для того, чтобы эти подклассы служили классами всех радикальных или классами всех полупростых алгебр для каких-либо Р. в . Такие подклассы алгебр принято называть соответственно радикальными и полупростыми подклассами.

Наследственные радикалы. Радикал r наз. идеальо наследственным радикалом, или кручением, в классе , если для всякого идеала I алгебры Аэтого класса: Идеально наследственные Р. есть в точности те Р., для к-рых классы (r). и (r) замкнуты относительно идеалов. Радикал rназ. наследственным, если класс (r) замкнут относительно идеалов. В классах ассоциативных, а также альтернативных алгебр каждый наследственный Р. является кручением. Радикал r наз. строго наследственным, если класс (r) замкнут относительно подалгебр.

Класс всех кручений является полной дистрибутивной «решеткой» (см. Дистрибутивная решетка). Употребление кавычек здесь связано с тем, что совокупность элементов этой «решетки» является не множеством, а классом.

Лит.:[1] A m i t s u r S. A., «Amer. J. Math.», 1952, v. 74, p. 774-86: 1954, v. 76, p. 100-36; [2] К у р о ш А. Г.,»Матем. сб.», 1953, т. 33, в. 1, с. 13-26; [3] D i v i n s k у N.. Rings and radicals, Toronto, 1965;[4] A r t i n E., N e s b i t t С., Т h o r a l l R., Rings with minimum condition, Ann Arbor, 1944; [5] Итоги науки. Алгебра. Топология. Геометрия. 1967, М., 1969, с. 28-32; [6] Кольца, т. 2, Новосиб., 1973, с. 3-6; [7] А н д р у н а к и е в и ч В. А., Р я б у х и н Ю. М., Радикалы алгебр и структурная теория, М., 1979; [8] Ж е в л а к о в К. А., С л и н ь к о А. М., Ш е с т а к о в И. П., Ширшов А. И., Кольца, близкие к ассоциативным, М., 1978.

Лит.:[1] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [2] Теория алгебр Ли. Топология групп Ли. Семинар «Софус Ли», пер. с франц., М., 1962; [3] Ш е в а л л е К., Теория групп Ли, пер. с франц., т. 3, М., 1958. А. Л. Онищик.

Источник

«Радикализм» в числах

В этом году исполнилось 350 лет со дня смерти Пьера де Ферма — одного из известнейших математиков прошлого. Ферма считается одним из создателей нескольких разделов математики: аналитической геометрии, математического анализа, теории вероятностей и теории чисел. К теории чисел можно отнести и знаменитую Великую теорему Ферма, которую он сформулировал в виде комментария на полях «Арифметики» Диофанта: «Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.» В «формульном» виде это выглядит так:

Для любого натурального n > 2 у уравнения a n + b n = c n нет ненулевых решений в целых числах a, b, c.

За три с лишним века, прошедших со времен Ферма, математика сильно развилась и изменилась. Возникло много новых разделов и направлений, а счет новым идеям и методам уже давно никто не ведет. Даже теорему Ферма доказали уже почти 20 лет назад (это сделал Эндрю Уайлс в 1995 году). Но, как это довольно часто случается, между разными понятиями и теориями, даже если их разделяет несколько веков, можно обнаружить неожиданные взаимосвязи. Увидеть маленький пример такой связи — неожиданный подход к теореме Ферма — позволит эта задача. Нам потребуется одно несложное определение.

Радикалом натурального числа n (обозначается rad(n)) называется произведение всех простых делителей числа n, взятых по одному разу. Например, rad(100) = 10, rad(7) = 7, а rad(48) = 6.

Задача

Существуют ли такие три попарно взаимно простых натуральных числа A, B, C, что A + B = C и при этом C > 1000·rad(A·B·C)?

Подсказка

Такие числа существуют.

Что делает операция взятия радикала с числом? Если в разложении числа на простые множители какие-то из множителей встречаются в высоких степенях, то эта операция сильно уменьшит такое число: ведь после нее каждый из таких множителей останется только в первой степени. Поэтому если удачно подобрать A, B и C и в каждом из этих чисел будут множители в высоких степенях, то rad(A·B·C) будет во много раз меньше произведения A·B·C и может оказаться меньше сомножителей. Так, что даже умножение на 1000 не спасет.

Если сразу подобрать такие числа не получается, то можно попробовать вместо 1000 взять коэффициент поменьше. Например, 10. Также, чтобы не возиться с взаимной простотой, можно положить B = 1. Это сразу обеспечит требуемую в условии попарную взаимную простоту всех трех чисел (подумайте, почему).

Решение

Следуя совету из подсказки, будем считать, что B = 1. Тогда C = A + B = A + 1. Поскольку разность двух чисел делится на любой общий делитель этих двух чисел, а у нас получилось, что C − A = 1, то числа A и C взаимно просты.

Пусть пока коэффициент перед радикалом равен 10. Попробуем найти такие числа A и C, что А + 1 = С и C > 10·rad(A·C). Будем действовать «методом тыка».

Пусть С = 100. Тогда А = 99, rad(A·C) = 330, 10·rad(A·C) = 3300. Не совсем то, что хочется. За таким выбором С никаких глубоких соображений не стоит, просто автору показалось, что удобно взять степень 10, так как справа стоит множитель 10. Попробуем взять С = 1000. Тогда А = 999, rad(A·C) = 1110, 10·rad(A·C) = 11 100. Уже лучше!

Что будет, если продолжать пробовать в качестве С брать всё более высокие степени 10? Кое-что про это понять довольно легко. Так как А и С взаимно просты, то

Ясно, что есть и другие примеры подходящих чисел. Наверняка можно подобрать гораздо меньшие числа. Но данный способ решения ценен тем, что в нем видны все этапы рассуждений: от «экспериментальных» данных через обобщение и формулировку гипотезы к полному решению, которое годится для любого коэффициента перед радикалом в правой части неравенства из условия.

Послесловие

Рассмотренная задача напоминает формулировку abc-гипотезы — не доказанного еще утверждения из теории чисел, которое было сформулировано в середине 1980-х годов. Вот формулировка этой гипотезы:

Из решения нашей задачи видно, что если в правой части неравенства взять первую степень радикала (то есть при ε = 0), то сразу окажется бесконечно много троек чисел A, B, C, которые нарушают это неравенство. А вот если ε > 0, то такого «раздолья» уже не будет: для каждого ε можно подобрать такую константу k (для разных ε константы будут разные), что какую бы мы не взяли тройку натуральных чисел, удовлетворяющих равенству A + B = C, для них обязательно будет выполняться указанное неравенство. Если, конечно, гипотеза верна. Верна она или нет — сейчас неизвестно. Пока никому не удалось ни доказать ее, ни опровергнуть.

Попытки доказать abc-гипотезу регулярно предпринимаются, но пока все тщетно. Последней, видимо, серьезной заявкой на успех было доказательство японского математика Синъити Мотидзуки, однако представленные им тексты настолько трудны для понимания даже ведущими специалистами, что, вероятно, в ближайшее время никто не сможет проверить, верно ли его доказательство или нет. Ну, а раз математическому сообществу проверить не удается, то это фактически означает, что доказательства нет. «The Paradox of the Proof» — не отягощенный серьезными математическими подробностями рассказ об этом всем (есть неплохой русский перевод этого текста).

Есть два довода в пользу того, что гипотеза верна. Оба они ни в коем случае не могут рассматриваться как серьезные аргументы — скорее, эти доводы вселяют слабую надежду в справедливость гипотезы. Первый — большое количество компьютерных вычислений по поиску связанных с гипотезой троек чисел. Ищут тройки, для которых ε был бы как можно больше, но пока даже значение ε = 0,7 не достигнуто. Кстати, каждый может поучаствовать в этом.

Второй довод в пользу справедливости гипотезы состоит в том, что из нее следуют многие очень сложные и глубокие теоремы и еще не доказанные гипотезы. Достаточно упомянуть лишь гипотезу Морделла (которую в 1983 году доказал Фальтингс, за что он получил Филдсовскую медаль). Подробнее об этом можно узнать из лекции Д. Орлова «АВС-гипотеза и ее следствия».

Доступность формулировки гипотезы чем-то напоминает историю с Великой теоремой Ферма, формулировка которой тоже понятна школьнику. Правда, в остальном эти утверждения скорее противоположны. Дело тут не в том, одно из них уже доказанная теорема, а про второе пока ничего не понятно. Важно значение для развития науки и тот способ, которым это значение достигается. Теорема Ферма несколько веков была притягательной задачей для многих ученых. В попытках ее доказать родилось много плодотворных идей и методов. А доказана она была с использованием мощнейшего аппарата алгебраической геометрии, который был создан в XX веке (подробнее об этом читайте в статье Ю. Соловьева «Гипотеза Таниямы и последняя теорема Ферма», а вся история этой теоремы изложена в книге С. Сингха «Великая теорема Ферма»). Но вот из самой теоремы Ферма никаких полезных следствий нет. В противоположность этому из abc-гипотезы, как уже говорилось, следует много важных и не очень фактов. В том числе — что если abc-гипотеза верна, то из нее буквально в несколько предложений следует Великая теорема Ферма. Вот как это получается.

Вот такое вот простое и понятное доказательство теоремы Ферма. Вряд ли француз имел в виду это доказательство в своем комментарии в книге Диофанта. Но мы можем теперь сказать, что почти знаем поистине чудесное доказательство этой теоремы, которое вполне можно уместить на полях. Осталось только доказать abc-гипотезу.

Рассмотренная задача предлагалась участникам LXXVII Московской математической олимпиады.

Источник

РАДИКАЛЫ

Общая теория радикалов. Всюду в дальнейшем говорится только об алгебрах (имеются в виду алгебры над произвольным фиксированным ассоциативно-коммутативным кольцом с единицей); кольца являются частным случаем таких алгебр. Под идеалом алгебры, если это не оговорено специально, понимается двусторонний идеал.

(A) гомоморфный образ r-алгебры есть r-алгебра;

(Б) каждая алгебра Акласса обладает наибольшим r-идеалом, т. е. идеалом, содержащим любой r-идеал этой алгебры, и этот максимальный r-идеал наз. тогда r-радикалом этой алгебры и обозначается r(А).

Алгебра, совпадающая со своим Р., наз. радикальной. В любом классе алгебр и для любого радикала <0>является единственной одновременно радикальной и полупростой алгеброй. Подпрямое произведение любого множества полупростых алгебр само полупросто.

С каждым радикалом r связаны два подкласса алгебр в : класс (r) всех r-радикальных алгебр и класс (r) всех r-полупростых алгебр. По любому из этих классов однозначно находится радикал r(А).для каждой алгебры Аиз , а именно:

Алгебра r-радикальна тогда и только тогда, когда она не может быть отображена гомоморфно ни на одну ненулевую r-полупростую алгебру.

Известны условия на подклассы алгебр, необходимые и достаточные для того, чтобы эти подклассы служили классами всех радикальных или классами всех полупростых алгебр для каких-либо Р. в . Такие подклассы алгебр принято называть соответственно радикальными и полупростыми подклассами.

Частичная упорядоченность радикальных классов по включению индуцирует частичный порядок на классе всех Р. в 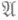. А именно, считается, что , если (r 1 ) содержит (r 2 ) (и в этом случае также (r 1 ) содержит (r 2 )).

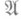
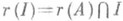
Наследственные радикалы. Радикал r наз. идеальо наследственным радикалом, или кручением, в классе , если для всякого идеала I алгебры Аэтого класса: Идеально наследственные Р. есть в точности те Р., для к-рых классы (r). и (r) замкнуты относительно идеалов. Радикал rназ. наследственным, если класс (r) замкнут относительно идеалов. В классах ассоциативных, а также альтернативных алгебр каждый наследственный Р. является кручением. Радикал r наз. строго наследственным, если класс (r) замкнут относительно подалгебр.

Класс всех кручений является полной дистрибутивной «решеткой» (см. Дистрибутивная решетка). Употребление кавычек здесь связано с тем, что совокупность элементов этой «решетки» является не множеством, а классом.

— верхний Р., определяемый классом всех матричных колец над телами;

В классе колец с условием минимальности первые семь Р. совпадают и соответствуют классическому Р. Если радикал r индуцирует в классе колец с условием минимальности классический Р., то . Для колец с условием максимальности . Для коммутативных колец , . Радикалы , являются специальными. Радикалы j, b, соответствуют одному и тому же разбиению простых колец, а -другим попарно различным разбиениям.

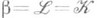
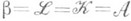
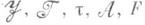
Лит.:[1] A m i t s u r S. A., «Amer. J. Math.», 1952, v. 74, p. 774-86: 1954, v. 76, p. 100-36; [2] К у р о ш А. Г.,»Матем. сб.», 1953, т. 33, в. 1, с. 13-26; [3] D i v i n s k у N.. Rings and radicals, Toronto, 1965;[4] A r t i n E., N e s b i t t С., Т h o r a l l R., Rings with minimum condition, Ann Arbor, 1944; [5] Итоги науки. Алгебра. Топология. Геометрия. 1967, М., 1969, с. 28-32; [6] Кольца, т. 2, Новосиб., 1973, с. 3-6; [7] А н д р у н а к и е в и ч В. А., Р я б у х и н Ю. М., Радикалы алгебр и структурная теория, М., 1979; [8] Ж е в л а к о в К. А., С л и н ь к о А. М., Ш е с т а к о в И. П., Ширшов А. И., Кольца, близкие к ассоциативным, М., 1978.

В классе алгебр Ли обычно радикалом наз. наибольший разрешимый идеал, т. е. разрешимый идеал r содержащий все разрешимые идеалы данной алгебры Ли. В конечномерной алгебре Ли существует также наибольший нильпотентный идеал n (называемый иногда нильрадикалом), к-рый совпадает с наибольшим идеалом, состоящим из нильпотентных элементов, а также с множеством таких , что присоединенный оператор adx содержится в Р. ассоциативной алгебры линейных преобразований пространства , порожденной присоединенной алгеброй Ли . Рассматривается также нильпотентный радикал алгебры Ли — это множество таких что s(x) = 0 для любого неприводимого конечномерного линейного представления s алгебры . Нильпотентный Р. совпадает также с наибольшим из идеалов, представляемых нильпотентными операторами при любом конечномерном линейном представлении алгебры При этом . Если характеристика основного поля равна 0, то — это наименьший из идеалов , для к-рых — редуктивная алгебра Ли. В этом случае нильпотентный Р. связан с радикалом r, соотношениями

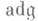
любое дифференцирование алгебры Ли переводит и . Нильрадикал и нильпотентный Р., однако, не являются Р. в смысле общей теории Р. колец и алгебр.

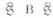
Лит.:[1] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [2] Теория алгебр Ли. Топология групп Ли. Семинар «Софус Ли», пер. с франц., М., 1962; [3] Ш е в а л л е К., Теория групп Ли, пер. с франц., т. 3, М., 1958. А. Л. Онищик.

Источник