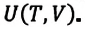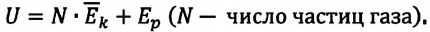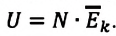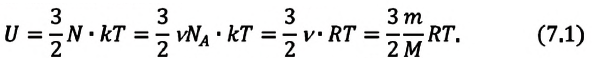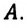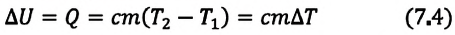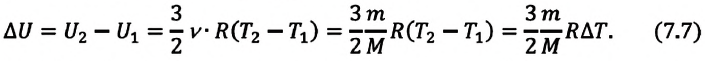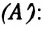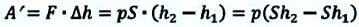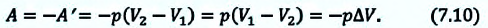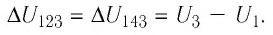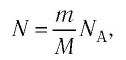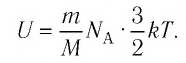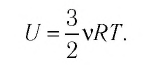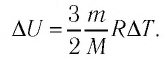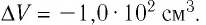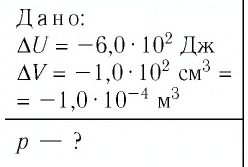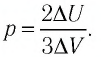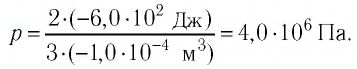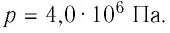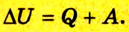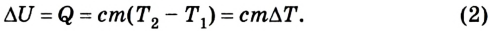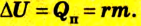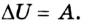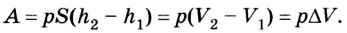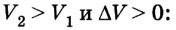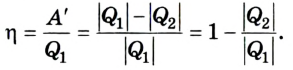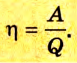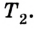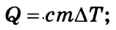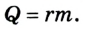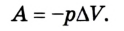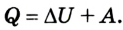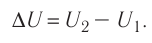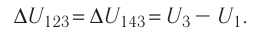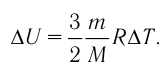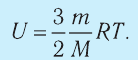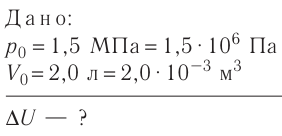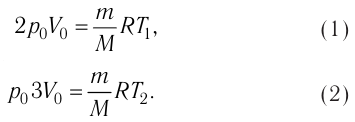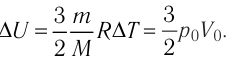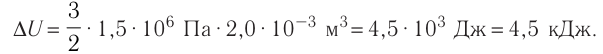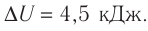что такое работа газа в физике определение

Что такое работа в физике? Работа сил, работа при расширении газа и работа момента силы

Работа как физическая величина

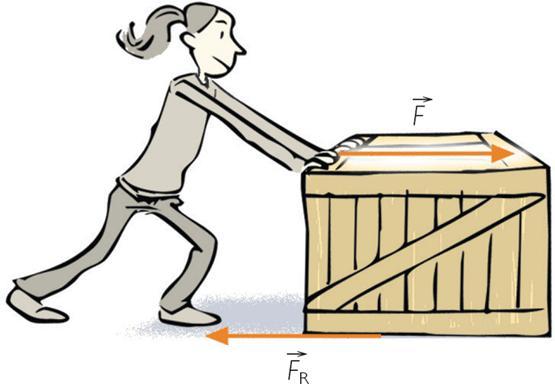
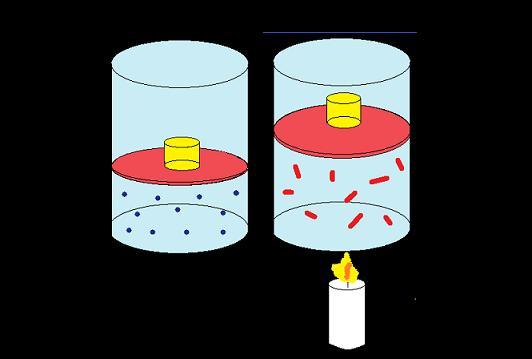
Отвечая на вопрос, что такое работа в физике, следует уточнить, что это энергия, которая затрачена на совершение каких-либо действий. Например, человек переносит груз с одного места на другое, при этом он совершает работу против сил трения. Если же этот человек начнет поднимать груз, то его работа будет направлена на преодоление силы тяготения планеты. Другой пример: газ, находящийся под поршнем, в результате нагрева начинает увеличивать свой объем, в таком случае говорят, что он совершает некоторую работу.

Вам будет интересно: Что такое педагогическое тестирование

Во всех перечисленных случаях присутствует одна общая черта: работа отличается от нуля только тогда, когда имеется какой-либо тип механического перемещения объектов или их частей (движение рабочего с грузом, расширение газа).

Формула работы

Теперь покажем, как количественно можно вычислить изучаемую величину. Перевод энергии между разными состояниями возможен только в том случае, если присутствует некоторая сила. Это может быть физическое усилие человеческих рук и ног, сила машин, создаваемое давление, которое легко пересчитывается в силу, в случае сгорания топлива в цилиндре, сила электромагнитной индукции электродвигателя и так далее.

На вопрос, как находить работу в физике, ответит следующая формула:

Здесь φ является углом между векторами силы F¯ и перемещения l¯.

Работа газа

Мы разобрали вопрос, что такое механическая работа в физике, и привели формулу, по которой ее можно вычислить. В случае расширения газов используют, однако, иное выражение.

Предположим, что у нас имеется газовая система, которая заполняет объем V1 и находится под давлением P. Пусть в результате какого-либо внешнего или внутреннего воздействия на систему ее объем изменился и стал равным V2. Тогда работу газа A можно определить по такой формуле:

Если изобразить на графике функцию P(V) в осях P-V, то площадь под кривой численно будет равна величине A.

В случае изобарного процесса (P = const) для идеального газа ответом на вопрос, как находить работу в физике, будет следующее простое выражение:

Если в результате термодинамического процесса объем газа не изменяется, то его работа будет равна нулю. Если V2>V1, то газ совершает положительную работу, если V1>V2, то отрицательную.

Работа момента силы

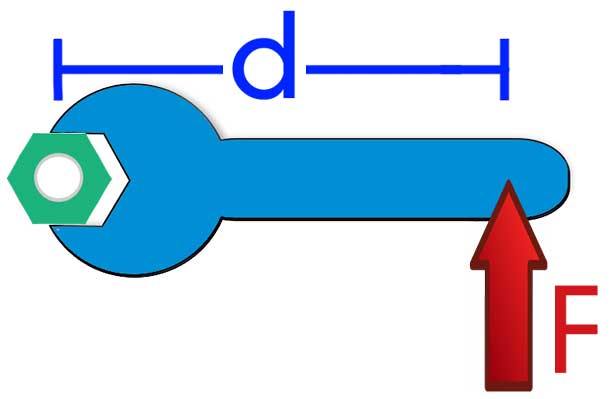
Моментом силы называется физическая величина, которая выражается следующей формулой:

То есть M равно векторному произведению силы F на радиус-вектор r относительно оси вращения. Момент силы выражается в Н*м.

Что такое в физике работа момента силы? На этот вопрос ответит следующая формула:

Это равенство означает, если момент M, действуя на систему, приводит к ее повороту вокруг оси на угол θ, то он совершает работу A. Угол θ здесь должен выражаться в радианах, чтобы получить работу в джоулях.

Вычисление работы момента силы играет важную роль во всех механических системах, где имеется вращение, например, колеса, шестерни, валы и так далее.

Работа силы тяжести

Разобравшись, что такое работа в физике, вычислим эту величину для сил тяготения. Предположим, что тело массой m падает с высоты h. Поскольку сила тяжести F действует вертикально вниз, то она совершает положительную работу. Определяется она по такой формуле:

Многие в полученной формуле для величины A могут увидеть выражение для потенциальной энергии тела, находящегося в поле сил гравитации. Во время падения тела сила тяжести совершает работу по переводу потенциальной энергии тела в кинетическую энергию его движения.

Источник

Внутренняя энергия и работа идеального газа

теория по физике 🧲 термодинамика

Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.

Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:

i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.

Изменение внутренней энергии идеального газа в изопроцессах

Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной.

Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.

Работа идеального газа

Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:

Перемещение равно разности высот поршня в конечном и начальном положении:

Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:

Работа идеального газа

p — давление газа, S — площадь поршня

Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:

A ‘ = p ( V 2 − V 1 ) = p Δ V > 0

Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.

Работа идеального газа при изобарном сжатии:

A ‘ = p ( V 2 − V 1 ) = p Δ V 0

Работа идеального газа при нагревании газа:

Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.

Геометрический смысл работы в термодинамике

В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).

Примеры графических задач

Изохорное охлаждение и изобарное сжатие:

Изобарное расширение:
Изобарное сжатие:
Изохорное охлаждение:
Замкнутый цикл: 1–2: A ‘ = ( p 1 − p 3 ) ( V 2 − V 1 )
Произвольный процесс:

Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A₂ к A₁ в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:

A 2 = p ( V 2 − V 1 ) = 4 p ( 5 V − 3 V ) = 4 p 2 V = 8 p V

A 1 = p ( V 2 − V 1 ) = p ( 5 V − V ) = 4 p V

Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?

Для каждой величины подберите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10 5 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10 5 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Источник

Что такое работа газа в физике определение

И сторическая справка.

1) М.В. Ломоносов, проведя стройные рассуждения и простые опыты, пришел к выводу, что «причина теплоты состоит во внутреннем движении частиц связанной материи… Весьма известно, что тепло возбуждается движением: руки от взаимного трения согреваются, дерево загорается, искры вылетают при ударе кремнием о сталь, железо накаливается при ковании его частиц сильными ударами»

2) Б. Румфорд, работая на заводе по изготовлению пушек, заметил, что при сверлении пушечного ствола он сильно нагревается. Например, он помещал металлический цилиндр массой около 50 кг в ящик с водой и, сверля цилиндр сверлом, доводил воду в ящике до кипения за 2.5часа.

3) Дэви в 1799 году осуществил интересный опыт. Два куска льда при трении одного о другой начали таять и превращаться в воду.

4) Корабельный врач Роберт Майер в 1840 году во время плавания на остров Яву заметил, что после шторма вода в море всегда теплее, чем до него.

В механике работа определяется как произведение модулей силы и перемещения: A=FS. При рассмотрении термодинамических процессов механическое перемещение макротел в целом не рассматривается. Понятие работы здесь связывается с изменением объема тела, т.е. перемещением частей макротела друг относительно друга. Процесс этот приводит к изменению расстояния между частицами, а также часто к изменению скоростей их движения, следовательно, к изменению внутренней энергии тела.

где ΔV — изменение объема газа. Если объем газа не изменяется (изохорный процесс), то работа газа равна нулю.

Почему при сжатии или расширении меняется внутренняя энергия тела? Почему при сжатии газ нагревается, а при расширении охлаждается?

Причиной изменения температуры газа при сжатии и расширении является следующее: при упругих соударениях молекул с движущимся поршнем их кинетическая энергия изменяется.

При сжатии и расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.

Работа внешних сил, действующих на газ

Запишем уравнение Клапейрона-Менделеева для двух состояний газа:

Следовательно, при изобарном процессе

Если m = М (1 моль идеального газа), то при ΔΤ = 1 К получим R = A. Отсюда вытекает физический смысл универсальной газовой постоянной: она численно равна работе, совершаемой 1 моль идеального газа при его изобарном нагревании на 1 К.

Геометрическое истолкование работы:

На графике p = f(V) при изобарном процессе работа равна площади заштрихованного на рисунке а) прямоугольника.

Если процесс не изобарный (рис. б), то кривую p = f(V) можно представить как ломаную, состоящую из большого количества изохор и изобар. Работа на изохорных участках равна нулю, а суммарная работа на всех изобарных участках будет равна площади заштрихованной фигуры. При изотермическом процессе (Т = const) работа равна площади заштрихованной фигуры, изображенной на рисунке в.

Источник

Содержание:

Термодинамические системы и макропараметры состояния вещества:

Внутреннее состояние тела очень сложно определить через параметры движения микрочастиц, потому что их очень много. Поэтому, чтоб упростить описание состояния термодинамической системы, его связывают с физическими величинами, которые характеризуют тело в целом, независимо от его молекулярного строения. К таким величинам принадлежат, в частности, масса, объем, плотность, давление, температура и т. п.
Их называют макропараметрами системы. Фактически они являются усредненными значениями данных физических величин на протяжении длительного времени.

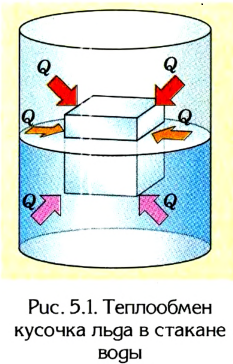
Например, из собственного опыта нам известно, что более нагретые тела отдают теплоту менее нагретым, вследствие чего со временем их температуры станут одинаковыми. Если, к примеру, кусочек льда бросить в стакан с теплой водой (рис. 5.1), то лед будет таять, а вода в стакане охлаждаться, отдавая определенное количество теплоты тающему льду. Кроме того, стакан с водой и лед пребывают в состоянии теплообмена с окружающей средой. Поэтому со временем температуры всех этих тел станут одинаковыми.

Тела с более высокой температурой отдают тепловую энергию телам с более низкой температурой; теплообмен происходит до тех пор, пока их температуры не станут одинаковыми.

Следовательно, со временем вследствие теплообмена в термодинамических системах наступает состояние термодинамического равновесия, когда температуры всех тел становятся одинаковыми и теплообмен между ними прекращается. Значение температуры характеризует вполне определенное состояние теплового равновесия термодинамической системы, в котором она пребывает в данный момент. Он может быть изменен в результате термодинамического процесса.

Термодинамика рассматривает в основном состояния термодинамического равновесия и процессы, которые происходят достаточно медленно, и поэтому каждое новое их состояние можно считать равновесным. В состоянии термодинамического равновесия между макропараметрами системы существуют определенные функциональные зависимости, отображаемые уравнениями состояния термодинамической системы.

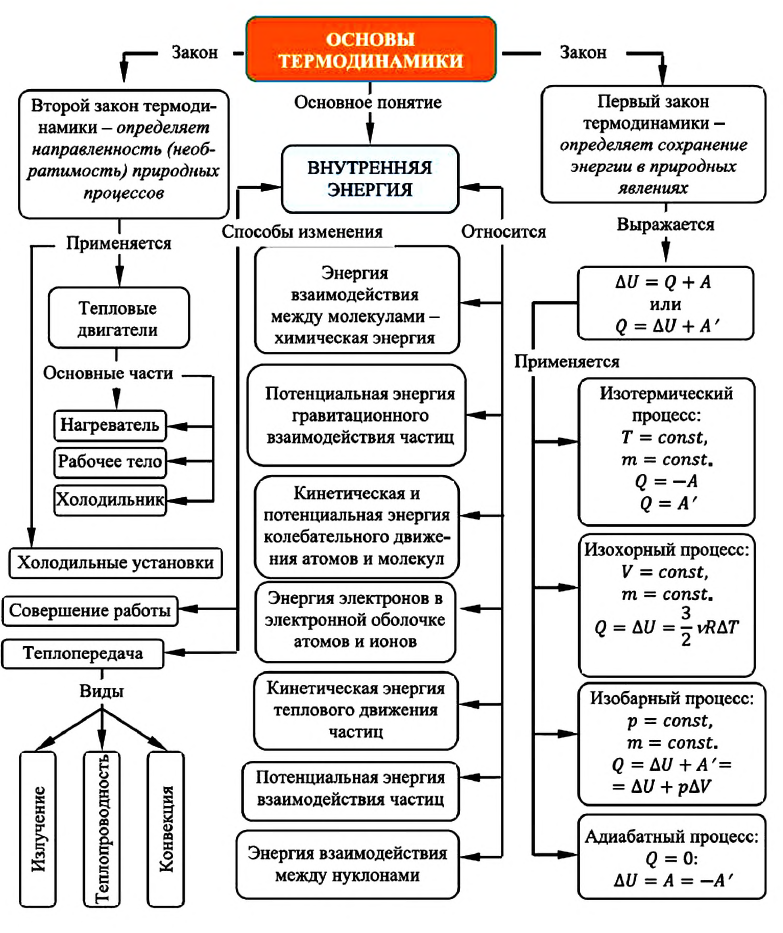
Карта основ термодинамики:

Термодинамическая система

Раздел физики, изучающий тепловые явления в макроскопических системах, называется термодинамикой. В основе термодинамики лежат термодинамические законы, опирающиеся на большое количество экспериментальных фактов. Эти законы отвечают на вопрос «как?», например, как изменяется состояние тела (твердого тела, жидкости или газа) при нагревании (или охлаждении), в каком направлении и как передается тепло, как изменяется температура газа при его расширении и другие. Объектами исследования термодинамики являются термодинамические системы.

Любое макроскопическое тело или система макроскопических тел называется термодинамической системой. Состояние термодинамической системы характеризуется макроскопическими или термодинамическими параметрами (масса, плотность, объем, давление, температура).

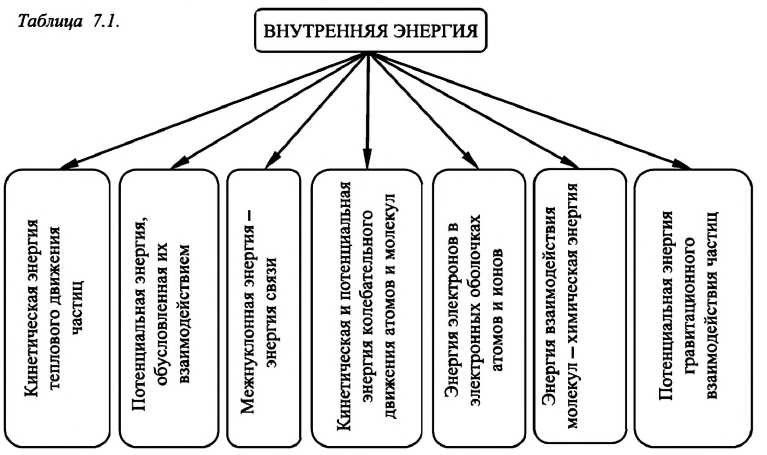
Внутренняя энергия

Величины, определяющие состояние термодинамической системы в данный момент времени, то есть соответствующие этому состоянию макроскопические параметры, называются функциями состояния. Основной среди этих величин является внутренняя энергия.

Внутренняя энергия термодинамической системы является функцией температуры и объема, определяющих состояние системы:

Внутренняя энергия одноатомного идеального газа

Газ, молекулы которого состоят из одного атома, называют одноатомным газом. Внутренняя энергия одноатомного газа равна сумме кинетических энергий поступательного движения частиц и потенциальных энергий их взаимодействия:

Однако внутренняя энергия идеального газа данной массы равна сумме средних кинетических энергий хаотического движения частиц:

Средняя кинетическая энергия одной частицы одноатомного идеального газа определяется выражением 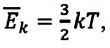следовательно, внутренняя энергия такого газа зависит только от температуры:

Это выражение является формулой закона Джоуля:

Внутренняя энергия идеального газа зависит от ее массы, рода (молярной массы) и температуры. Даже если давление и объем газа изменятся, при постоянной температуре его внутренняя энергия не изменится.

Сопоставив формулу (7.1) с выражением Менделеева-Клапейрона, получим:

Способы изменения внутренней энергии

Для изменения внутренней энергии термодинамической системы необходимо изменить или среднюю кинетическую энергию теплового движения молекул системы, или потенциальную энергию их взаимодействия, или же изменить обе энергии одновременно. Из многочисленных опытов было определено, что существует два способа изменения внутренней энергии: теплопередача и совершение работы.

Изменение внутренней энергии системы происходит двумя способами: передачей количества теплоты 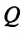и совершением работы

Если внутренняя энергия изменяется только в результате теплообмена, то изменение внутренней энергии равно полученному (или отданному) системой количеству теплоты. Например, при нагревании и охлаждении тела изменение его внутренней энергии определяется так:

Изменение внутренней энергии в процессе плавления твердого тела или кристаллизации жидкости происходит за счет изменения потенциальной энергии взаимодействия молекул тела. Изменение внутренней энергии при этих процессах численно равно теплоте плавления (кристаллизации):

Где 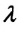— удельная теплота плавления.

Изменение внутренней энергии тела в процессе парообразования и конденсации также равно затраченному во время этого процесса количеству теплоты:

Где 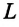— удельная теплота парообразования.

Изменение внутренней энергии одноатомного идеального газа определяется изменением его температуры:

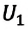
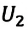
Где и — соответственно, значения внутренней энергии одноатомного газа в начальном и конечном состояниях.

Внимание. Изменение внутренней энергии термодинамической системы зависит не от вида процесса, а от его начального и конечного состояния.

Работа в термодинамике

Если изменение внутренней энергии происходит только в результате совершения механической работы, то это изменение равно или работе внешних сил над системой 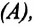или работе системы против внешних сил

Работа в термодинамике — это одна из мер изменения внутренней энергии термодинамической системы.

Работа газа

Таким образом, работа, совершенная газом над внешними силами, в результате расширении газа данной массы при постоянном давлении равна:

Работа же, совершенная внешними силами над газом равна :

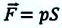
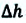
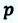
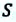
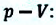
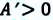
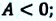
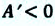
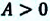
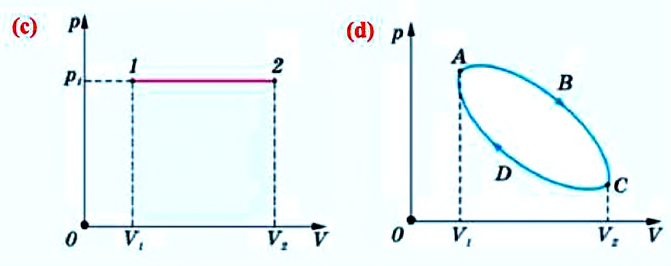
Где — сила, с которой газ действует на поршень, — смещение поршня, — давление газа, — площадь поперечного сечения цилиндра, — изменение объема газа. Совершенная работа численно равна площади фигуры, образованная графиком в системе координат при расширении газа (т.е. при увеличении объема газа) или при сжатии же газа (т.е. при уменьшении объема газа) или (с).

Если в процессе совершения работы газ через некоторое время возвращается в первоначальное состояние, то такой процесс называется замкнутым или циклическим процессом.

Если стрелки, показывающие направление циклического процесса, совпадают с направлением вращения часовых стрелок, то работа газа положительна, а работа внешних сил отрицательна (d). Если же стрелки, определяющие направление процесса, направлены против вращения часовых стрелок, то работа газа отрицательна, а работа внешних сил положительна.

Что такое термодинамическая система

Полную энергию физической системы можно представить как алгебраическую сумму её механической энергии и внутренних энергий тел, образующих систему. Убыль механической энергии системы в ряде случаев происходит при самопроизвольном переходе её части во внутреннюю энергию тел системы. Так, например, режущие инструменты заметно нагреваются при заточке. При скольжении конькобежца под коньками тает лёд, что обеспечивает хорошее скольжение. В этих примерах тела при трении нагреваются, и интенсивность теплового движения их молекул возрастает, что приводит к увеличению внутренней энергии тел. Как же определить внутреннюю энергию термодинамической системы? И что понимают под термодинамической системой?

В термодинамике физические тела и их модели называют термодинамическими системами. Для их описания используют параметры системы, такие, как давление, объём, температура (макропараметры), а не физические характеристики молекул (микропараметры). Макропараметры можно непосредственно измерить, используя приборы, или выразить через другие величины, которые можно измерить на опыте. Мы рассмотрим простейшие термодинамические системы, состояние которых определяют, используя только давление, объём и температуру.

Тела, образующие термодинамическую систему, могут обмениваться с окружающей средой энергией, а также веществом. Если этого не происходит, то термодинамическую систему называют замкнутой или изолированной.

Что такое внутренняя энергия

Рассматривая полную энергию макроскопического тела, необходимо учитывать не только его механическую энергию (кинетическую и потенциальную), но также и энергию, заключённую внутри самого тела, — внутреннюю энергию.

Внутренняя энергия макроскопического тела — алгебраическая сумма кинетической энергии теплового движения всех частиц, образующих тело, и потенциальной энергии их взаимодействия.

Внутренняя энергия любой термодинамической системы состоит из внутренних энергий тел, входящих в данную систему, и является одной из основных физических величин, используемых в термодинамике.

В термодинамике представляет интерес не само значение внутренней энергии системы, а её изменение. Поэтому обычно принимают во внимание только те составляющие внутренней энергии, которые изменяются в рассматриваемых процессах.

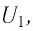
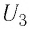
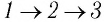
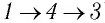
Рассмотрим переход некоторой массы идеального газа из состояния 1, в котором его внутренняя энергия в состояние 3, в котором его внутренняя энергия (рис. 62). Смену состояний можно осуществить или при изохорном нагревании, а затем при изобарном расширении (процесс ), пли при изобарном расширении, а затем при изохорном нагревании (процесс ). Однако приращение* внутренней энергии газа в обоих случаях одинаково:

Внутренняя энергия зависит от конкретного состояния системы. Это означает, что изменение внутренней энергии при переходе термодинамической системы из одного состояния в другое зависит только от значений параметров этих состояний и не зависит от процесса перехода.

Внутренняя энергия идеального одноатомного газа

Определим внутреннюю энергию идеального одноатомного газа, т. е. газа, образованного атомами. Например, одноатомными газами являются инертные газы — гелий, неон, аргон и др.

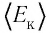
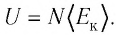
Из определения понятия «идеальный газ» следует, что его внутренняя энергия является суммой кинетических энергий хаотического движения всех атомов (или молекул) (потенциальная энергия взаимодействия между частицами отсутствует). Следовательно, внутренняя энергия идеального одноатомного газа равна произведению средней кинетической энергии теплового движения частиц на их число N, т. е. Поскольку

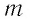
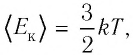
где — масса газа, а то

С учётом того, что произведение постоянной Больцмана и постоянной Авогадро 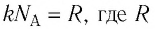— универсальная газовая постоянная, получим:

Из формулы (11.1) следует, что внутренняя энергия данной массы идеального одноатомного газа пропорциональна его абсолютной температуре. Она не зависит от других макроскопических параметров состояния — давления и объёма. Следовательно, изменение внутренней энергии данной массы одноатомного идеального газа происходит только при изменении его температуры:

При определении внутренней энергии реальных газов, жидкостей и твёрдых тел необходимо учитывать потенциальную энергию взаимодействия частиц, которая зависит от расстояния между ними. Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.

Изменить внутреннюю энергию термодинамической системы можно двумя способами: используя теплообмен и совершая работу. Процесс теплообмена и совершение работы характеризуют соответственно физическими величинами — количеством теплоты Q и работой А, которые являются мерами изменения внутренней энергии системы.

Пример решения задачи №1

При изобарном охлаждении внутренняя энергия идеального одноатомного газа изменилась на 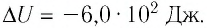Определите давление газа, если его объём изменился на

Решение. Приращение внутренней энергии некоторого количества идеального одноатомного газа

Используя уравнение Клапейрона—Менделеева, можно осуществить замену:

Решая совместно уравнения (1) и (2), получим:

Ответ:

Внутренняя энергия тела

Любое макроскопическое тело обладает энергией, что обусловлено его микросостоянием. Эта энергия называется внутренней (обозначается U). Она равна энергии всех микрочастиц вещества, из которых состоит данное тело. Например, внутренняя энергия идеального газа состоит из кинетической энергии всех его молекул, без учета их потенциальной энергии, поскольку взаимодействием молекул в модели идеального газа пренебрегают.

Модель идеального газа предусматривает, что молекулы пребывают на расстоянии нескольких диаметров друг от друга. Поэтому энергия их взаимодействия намного меньше энергии их движения, следовательно, ею можно пренебречь.

В реальных газах, а также в жидкостях и твердых телах внутреннюю энергию необходимо учитывать, потому что она соизмерима с кинетической энергией и существенно влияет на их свойства. В таком случае их внутренняя энергия состоит из кинетической энергии теплового движения микрочастиц и потенциальной энергии их взаимодействия.

Изменение внутренней энергии тела может произойти за счет теплообмена или в результате выполнения работы:

Следовательно, передача количества теплоты и выполнение работы являются факторами, благодаря которым можно изменить внутреннюю энергию тела:

В случае, когда происходит лишь теплообмен, полученное или отданное телом количество теплоты полностью идет на изменение его внутренней энергии, в частности кинетической энергии его атомов и молекул: 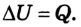Во время нагревания или охлаждения тела она равна:

В процессе плавления или кристаллизации твердых тел внутренняя энергия изменяется за счет потенциальной энергии взаимодействия микрочастиц, потому что происходит структурная перестройка вещества. В данном случае изменение внутренней энергии равно теплоте плавления (кристаллизации) тела:

где 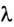— удельная теплота плавления (кристаллизации) твердого тела.

Если изменение внутренней энергии тела происходит вследствие теплообмена, то или или

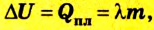
Изменение внутренней энергии тела вследствие выполнения механической работы (без теплообмена) равно значению работы:

Следовательно, с точки зрения молекулярной физики внутренняя энергия тела является суммой кинетической энергии теплового движения атомов, молекул и других частиц, из которых оно состоит, и потенциальной энергии их взаимодействия. Это энергия термодинамической системы, которая зависит от ее внутреннего состояния. Поэтому вычисляют изменение внутренней энергии 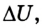которое происходит в результате теплообмена или выполнения работы, а не само ее значение U.

Работа газа

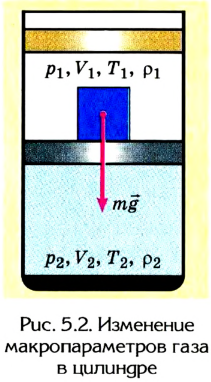
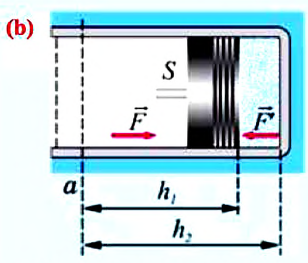
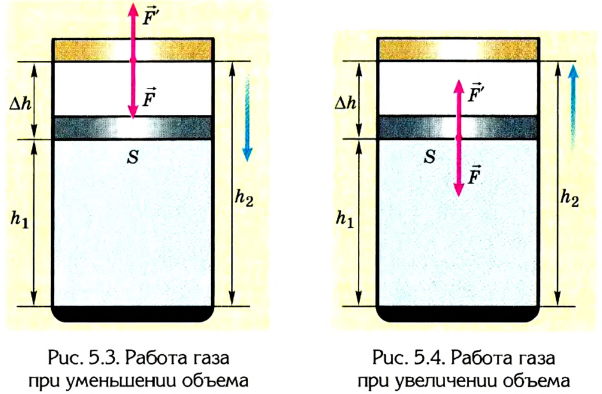
Вычисление выполненной работы в термодинамике связывают с макропараметрами системы. Рассмотрим газ, находящийся в цилиндре под поршнем площадью S (рис. 5.3).

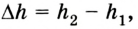
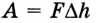
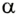
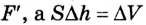
Пусть на газ действует поршень, вызывая его сжатие. Под действием силы F поршень опускается на высоту выполняя работу (направление действия силы имеет то же направление, что и перемещение, поэтому cos — 1). Если перемещение поршня будет незначительным, то давление газа практически не изменится (р = const). Учитывая, что согласно третьему закону Ньютона сила F по модулю равна силе давления газа — это изменение объема газа, получим:

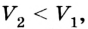
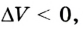
Поскольку следовательно, то работа внешних сил над газом будет равна:

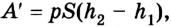
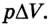
Если под действием силы давления F’ газ расширяется (рис. 5.4), т. е. он сам выполняет работу то ее значение также равно Выполненная газом работа в данном случае будет положительной, поскольку

Во время незначительных изменений объема и при постоянном давлении формулы (1) и (2) справедливы не только для газов, но и иных термодинамических систем. Поскольку изменение объема при постоянном давлении сопровождается изменением температуры тела, то можно сделать вывод, что выполнение работы в термодинамике вызывает изменение состояния тела, ведь при этом изменяются его температура Т и объем V.

Первый закон термодинамики

Позже этот фундаментальный закон природы приобрел логическую форму первого закона термодинамики: переход термодинамической системы из одного состояния в другое характеризуется изменением ее внутренней энергии, равной сумме работы внешних сил и количества теплоты, переданной системе:

т. е. передача термодинамической системе определенного количества теплоты вызывает изменение ее внутренней энергии или выполнение работы, либо то и другое одновременно.

Еще в 1775 г. Французская академия наук приняла решение не рассматривать проекты вечных двигателей.

Последняя формулировка первого закона термодинамики важна с точки зрения отрицания возможности создания вечного двигателя: нельзя создать машину, которая бы неограниченно выполняла работу, не получая энергию извне. Ведь, если количество теплоты Q = 0, то А’ = 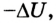т. е. работа выполняется за счет уменьшения внутренней энергии, которая не безгранична по размеру.

Тепловые двигатели

Человечество научилось использовать тепловую энергию, создав тепловые машины и двигатели. В основу их действия положена идея, что выполнение механической работы может осуществляться за счет теплоты, получаемой от какого-либо нагревателя и частично отдаваемой холодильнику.

Принцип действия тепловой машины можно представить схематически (рис. 5.5). Нагреватель передает рабочему телу определенное количество теплоты 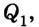часть которой идет на выполнение работы А’. Рабочим телом в тепловых машинах

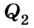
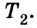
Выполняя работу, рабочее тело отдает определенную часть количества теплоты охладителю (специальному устройству или окружающей среде), вследствие чего его температура снижается до значения Оно не может использовать всю предоставленную тепловую энергию, поскольку часть ее рассеивается в окружающей среде из-за выбросов отработанного пара или выхлопных газов.

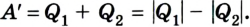
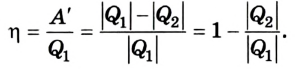
Согласно закону сохранения энергии значение выполненной работы По определению коэффициент полезного действия равен:

Коэффициент полезного действия равен отношению величины выполненной работы к затраченной при этом энергии:

Холодильник также является тепловой машиной. Принцип его действия основан на обратимости цикла тепловой машины. Холодильная машина работает как тепловой насос: она отбирает тепловую энергию у менее нагретого тела и передает ее более нагретому (рис. 5.6). Это не противоречит законам термодинамики, поскольку охлаждение происходит за счет выполнения работы.

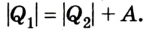
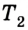
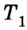
Для того чтобы привести в действие холодильную машину, необходимо над рабочим телом выполнить работу. В таком случае нагревателю будет передаваться количество теплоты, превышающее по значению то, которое отбирается у охладителя: Следовательно, температура охладителя будет еще больше снижаться, а температура нагревателя при этом будет повышаться.

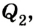
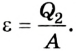
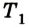
Эффективность работы холодильной машины характеризуется отношением количества теплоты отобранного у тела, к выполненной при этом работе А: Данный коэффициент может быть больше 1. Он зависит от разницы температур нагревателя и охладителя

Основные определения и формулы

Внутренняя энергия тела равна энергии всех микрочастиц вещества, из которых оно состоит. Ее можно изменить за счет теплообмена или в результате выполнения работы. Количество теплоты, переданное телу (либо отобранное у него), определяется в зависимости от теплового процесса, который при этом осуществляется:

при нагревании (охлаждении )

при плавлении (кристаллизации )

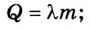
при парообразовании (конденсации)

Работа газа при постоянном давлении (р = const) равна: 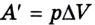и изменяет знак на противоположный при выполнении работы внешними силами над газом:

Первый закон термодинамики устанавливает, что количество теплоты, переданное термодинамической системе, вызывает изменение ее внутренней энергии или выполнение работы, либо и той другое одновременно:

Он отражает сущность фундаментального закона сохранения энергии, которым отрицается возможность создания вечного двигателя: нельзя создать машину, которая неограниченно выполняла бы работу, не получая энергию извне.

Законы термодинамики получили широкое практическое применение, в частности, в технике, при конструировании тепловых машин. Все тепловые машины (двигатели внутреннего сгорания, реактивные двигатели, паровые и газовые турбины, холодильные машины и пр.) построены по принципу выполнения механической работы за счет внутренней энергии. Их КПД всегда меньше 1 и равен:

Основы термодинамики

В 9 классе вы узнали, что полная энергия физической системы представляет собой сумму её механической энергии и внутренних энергий тел, образующих систему. Причём изменение механической энергии в ряде случаев происходит в результате перехода её части во внутреннюю энергию тел системы. Режущие инструменты заметно нагреваются при заточке их на точильном камне. При скольжении конькобежца по льду под коньками тает лёд, что обеспечивает хорошее скольжение. В этих примерах тела при трении нагреваются, и интенсивность хаотического движения молекул возрастает, что приводит к увеличению внутренней энергии тел. Как же определить внутреннюю энергию термодинамической системы? И что понимают под термодинамической системой?

Выводы термодинамики основаны на фундаментальных законах, называемых началами термодинамики. Эти законы установлены в результате обобщения многочисленных экспериментальных фактов. Опираясь на них, термодинамика позволяет делать определённые выводы о свойствах исследуемых систем, которые подтверждаются экспериментально. Физические тела и их модели в термодинамике называют термодинамическими системами. Термодинамическую систему характеризуют набором параметров, определяющих её состояние. В отличие от молекулярно-кинетической теории в термодинамике не рассматривают микроскопическое строение тел и для их описания используют не физические характеристики молекул (микропараметры), а параметры системы (макропараметры), такие как давление, объём, температура.

Замкнутая, или же изолированная, термодинамическая система стремится к равновесию, когда все её макропараметры не изменяются с течением времени. Иначе говоря, для каждой изолированной термодинамической системы существует состояние термодинамического равновесия, в которое она переходит самопроизвольно.

Это утверждение называют нулевым началом термодинамики.

Говоря о полной энергии макроскопического тела, необходимо всегда учитывать не только его механическую энергию (кинетическую и потенциальную), но также кинетическую энергию теплового движения его частиц и потенциальную энергию их взаимодействия. В термодинамике под внутренней энергией тела понимают полную энергию, относящуюся к самим частицам, образующим тело. Это кинетическая энергия теплового движения молекул, кинетическая энергия движения атомов внутри молекул, потенциальная энергия взаимодействия между молекулами, энергия электронных оболочек атомов и внутриядерная энергия.

Внутренняя энергия любой термодинамической системы состоит из внутренних энергий тел, входящих в данную систему.

В термодинамике главную роль играет не сама внутренняя энергия, а её изменение, которое происходит при переходе системы из одного состояния в другое. Под приращением (изменением) внутренней энергии понимают разность внутренних энергий в конечном и начальном состояниях:

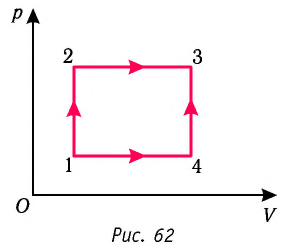
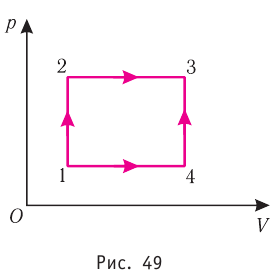
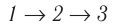
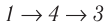
Например, переход некоторой массы идеального газа из состояния / в состояние 3 (рис. 49) можно осуществить или в ходе процесса (при изохорном нагревании, а затем при изобарном расширении), или в ходе процесса (при изобарном расширении, а затем при изохорном нагревании). Однако приращение (изменение) внутренней энергии газа и в одном и в другом случае будет одинаковым:

Внутренняя энергия является функцией состояния системы. Это означает, что изменение внутренней энергии при переходе термодинамической системы из одного состояния в другое зависит только лишь от значений параметров этих состояний, а не от процесса перехода.

Внутренняя энергия идеального одноатомного газа:

Определим внутреннюю энергию идеального одноатомного газа, т. е. газа, состоящего из отдельных атомов. Например, к одноатомным газам относят инертные газы — гелий, неон, аргон и др.

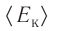
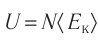
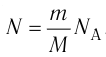
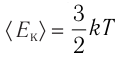
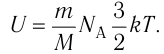
Из определения понятия «идеальный газ» следует, что его внутренняя энергия является суммой кинетических энергий хаотического движения всех молекул или атомов (взаимодействие между частицами отсутствует). Следовательно, внутренняя энергия идеального одноатомного газа равна произведению средней кинетической энергии теплового движения частиц на их число N,

т. е. . Поскольку , где m — масса газа, а , то

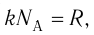
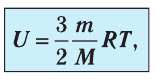
С учётом того, что получим:
(9.1)
или

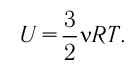
Как видно из формулы (9.1), внутренняя энергия данной массы идеального одноатомного газа пропорциональна абсолютной температуре газа. Она не зависит от других макроскопических параметров состояния — давления и объёма. Следовательно, изменение внутренней энергии данной массы идеального одноатомного газа происходит только при изменении его температуры: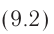

При определении внутренней энергии реальных газов, жидкостей и твёрдых тел необходимо учитывать потенциальную энергию взаимодействия частиц, которая зависит от расстояния между ними. Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.

При изучении физики в 8 классе вы узнали, что изменить состояние термодинамической системы можно двумя способами: используя теплопередачу и совершая работу. Процесс теплопередачи и совершение работы характеризуют соответственно физическими величинами — количеством теплоты Q и работой А, которые являются мерами изменения внутренней энергии системы.

Пример решения задачи №2

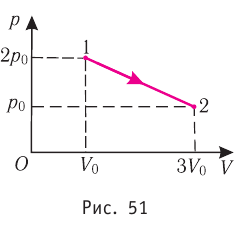
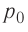
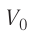
На рисунке 51 в координатах (р, V) изображён процесс перехода идеального одноатомного газа определённой массы из состояния 1 в состояние 2. Определите приращение внутренней энергии газа, если давление газа в конечном состоянии = 1,5 МПа, а его объём в начальном состоянии = 2,0 л.

Приращение внутренней энергии идеального одноатомного газа 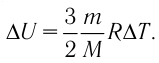Найти массу m газа, его молярную массу M и

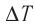
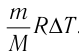
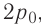
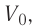
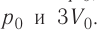
изменение температуры не представляется возможным. Однако, используя уравнение Клапейрона—Менделеева, для состояний 1 и 2 можно определить значение выражения . Из рисунка 51 видно, что в состоянии 1 давление газа а его объём а в состоянии 2 — Тогда уравнение Клапейрона—Менделеева для состояний 1и 2 примет вид:

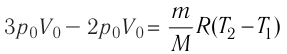
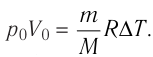
Вычтем из уравнения (2) уравнение (1): и получим, что . Тогда

Ответ:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник