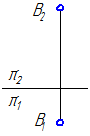что такое прямая общего положения

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

2.3. Частные положения прямой в пространстве

.

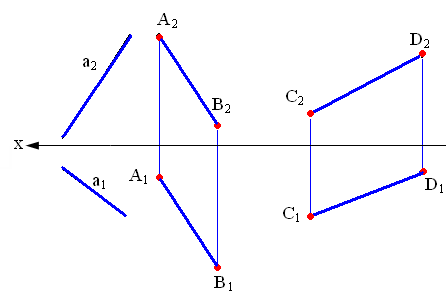
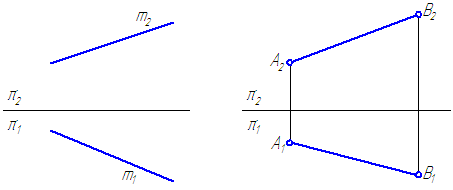
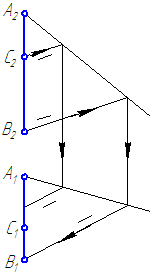
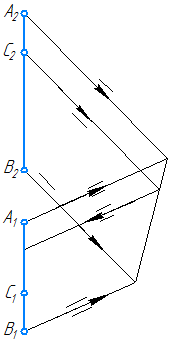
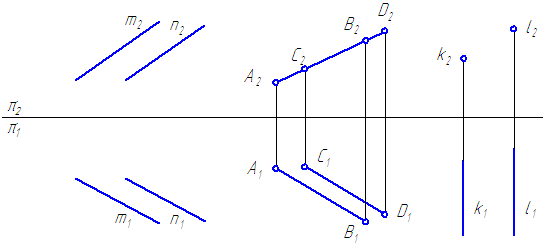
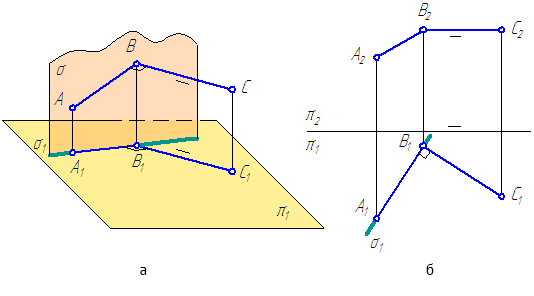
Рис. 2.1. Прямые общего положения

На рис. 2.1 показаны прямые общего положения, т. е. прямые, произвольно расположенные относительно плоскостей проекций.

Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.

Рассмотрим изображение на эпюре и отметим основные свойства этих прямых.

Прямые, параллельные плоскостям проекций.

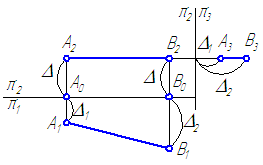
1. Горизонтальная прямая h (рис. 2.2) – горизонталь

Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций π₁.

Так как все точки этой прямой равноудалены от плоскости проекций π₁ (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π₁ проецируются без искажения отрезок прямой АВ (А₁В₁=АВ) и углы наклона прямой к плоскостям проекций π₂ и π₃ (углы β 0 и γ 0 ).

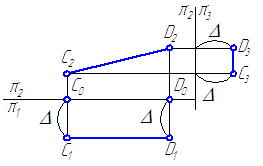
2. Фронтальная прямая f (рис. 2.3) – фронталь

Фронтальная прямая – это прямая параллельная фронтальной плоскости проекций π₂. Так как все точки этой прямой равноудалены от плоскости проекций π₂ (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π₂ проецируются без искажений отрезок этой прямой CD (C₂D₂+CD) и углы наклона прямой к плоскостям проекций π₁ и π₃ (углы α 0 и γ 0 )

.

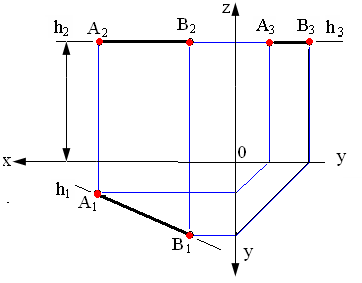
Рис. 2.2. Горизонтальная прямая

3. Профильная прямая p (рис. 2.4)

Прямые, принадлежащие плоскостям проекций

Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых. Характерным признаком для эпюра, на котором изображена подобная прямая будет принадлежность одной из проекций прямой соответствующей оси.

.

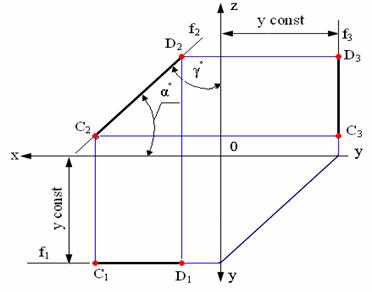
Рис. 2.3. Фронтальная прямая

.

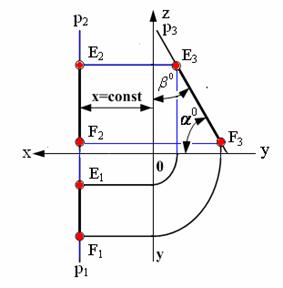
Рис. 2.4. Профильная прямая

На рис. 2.5, 2.6, 2.7 показаны прямые, принадлежащие соответственно горизонтальной плоскости проекций (частный случай горизонтальной прямой Z=0), фронтальной плоскости проекций (частный случай фронтальной прямой Y=0) и профильной плоскости проекций (частный случай профильной прямой Х=0).

.

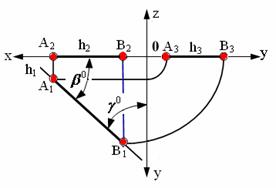
Рис. 2.5. Прямая, принадлежащая горизонтальной плоскости проекций

.

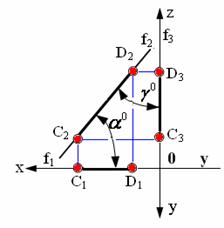
Рис. 2.6. Прямая, принадлежащая фронтальной плоскости проекций

.

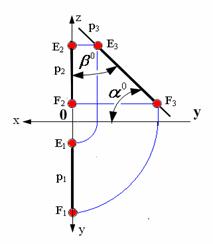
Рис. 2.7. Прямая, принадлежащая профильной плоскости проекций

Прямые, перпендикулярные плоскостям проекций.

На рис. 2.8 и 2.9 показаны прямые, перпендикулярные соответственно горизонтальной и фронтальной плоскостям проекций

Прямая перпендикулярная горизонтальной плоскости проекций – горизонтально-проецирующая прямая. Такая прямая проецируется на плоскость π₁ в точку; ее фронтальная проекция перпендикулярна оси Х (рис. 2.8).

Прямая, перпендикулярная фронтальной плоскости проекций – фронтально-проецирующая прямая. Эта прямая проецируется на плоскость π₂ в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9).

Прямая, перпендикулярная профильной плоскости проекций – профильно-проецирующая прямая. Эта прямая проецируется на плоскость π₃ в точку, а ее фронтальная проекция перпендикулярна оси Z.

Эти прямые являются частными случаями фронтали и горизонтали.

.

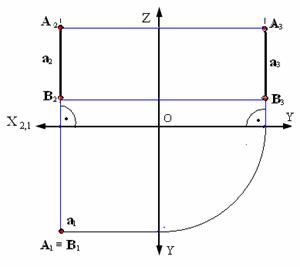
Рис. 2.8. Прямая, перпендикулярная горизонтальной плоскости проекций

.

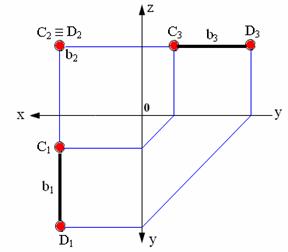
Рис. 2.9. Прямая, перпендикулярная фронтальной плоскости проекций

.

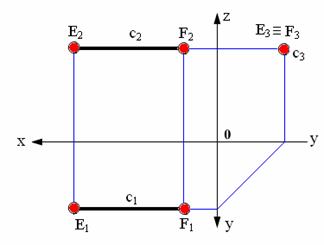
Рис. 2.10. Прямая, перпендикулярная профильной плоскости проекций

Источник

Что такое прямая общего положения

Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.

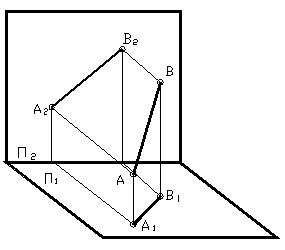
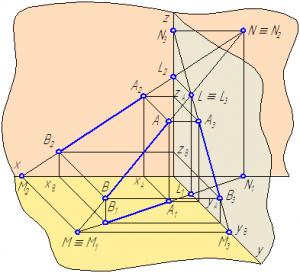
Рисунок 8

а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.

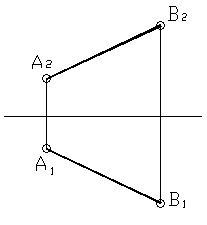
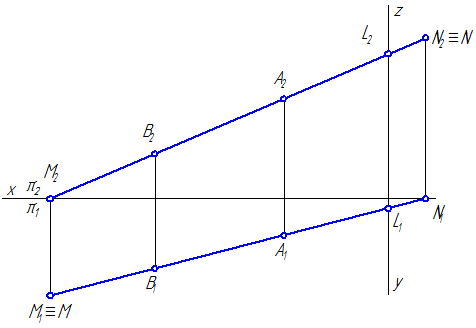
Рисунок 9

б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

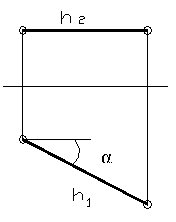
Рисунок 10

Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.

Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

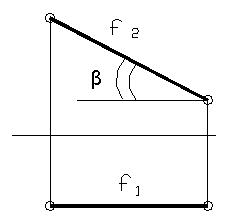
Рисунок 11

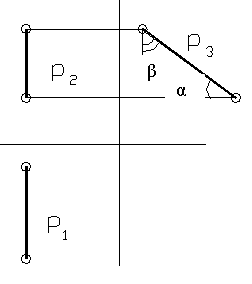
Рисунок 12.

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).

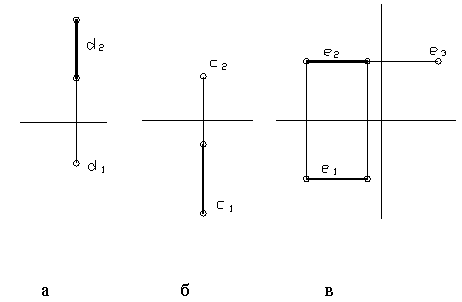
Рисунок 13

Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

а) три точки, не лежащие на одной прямой;

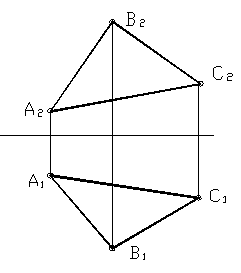
Рисунок 14

б) прямая и точка, не лежащая на ней;

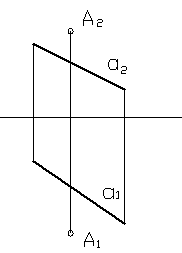
Рисунок 15

в) две параллельные прямые;

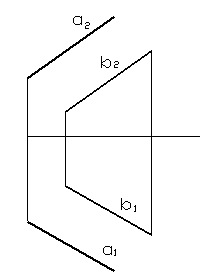
Рисунок 16

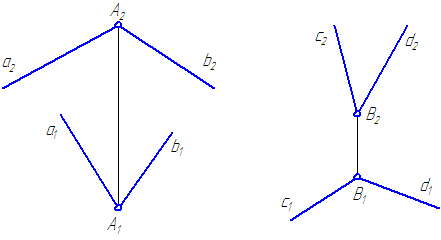
г) две пересекающиеся прямые;

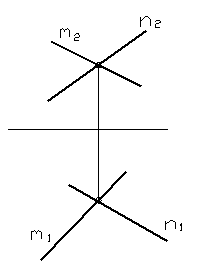
Рисунок 17

д) плоская фигура (многоугольник, круг и т.д.).

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

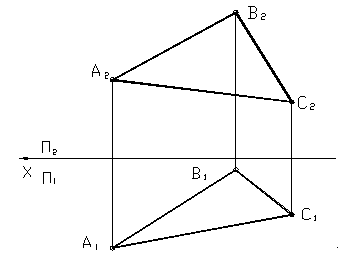
Рисунок 18

Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.

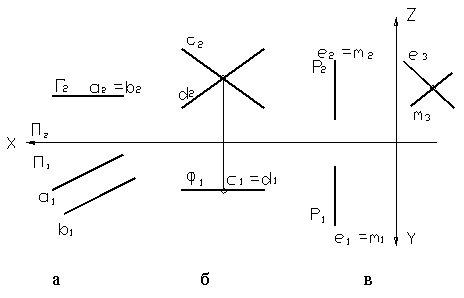
Рисунок 19

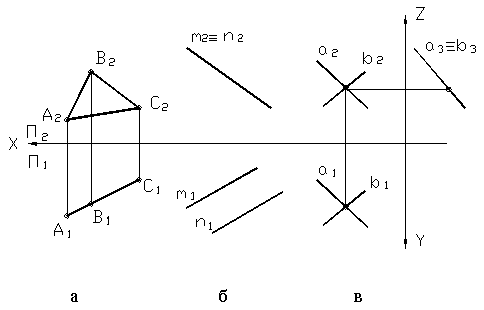
Рисунок 20

1. Как образуется комплексный чертеж прямой линии?

2. Прямые какого положения вы знаете?

3. Назовите прямые уровня.

4. Как называется прямая, проекцией которой на горизонтальной плоскости будет точка?

5. Перечислите способы задания плоскости.

6. Дайте определение плоскости общего положения.

7. Какие бывают плоскости частного положения? Как они называются и как выглядят на комплексном чертеже?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Лекция 2. Ортогональные проекции прямой

2.1. Задание прямой на эпюре

Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.

а б
Рисунок 2.1 – Проекции прямой

Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.

Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.

2.2. Прямые частного положения

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).

Рисунок 2.2 – Эпюр горизонтали

Если отрезок параллелен плоскости проекций π₁, то его фронтальная проекция А₂В₂ параллельна оси проекций π₁/π₂, а горизонтальная проекция отрезка А₁В₁ определяет истинную величину АВ:

Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).

Рисунок 2.3 – Эпюр фронтали

Если отрезок параллелен плоскости проекций π₂, то его горизонтальная проекция параллельна оси проекций π₂/π₁, а фронтальная проекция отрезка C₂D₂ определяет истинную величину CD.

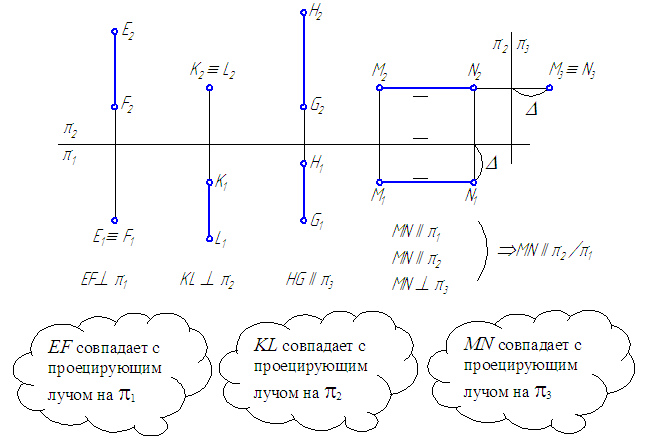
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).

Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).

Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).

Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).

Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH

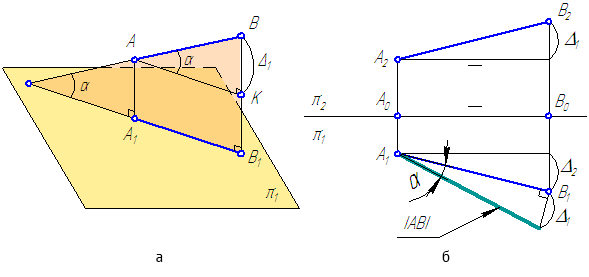
2.3. Метод прямоугольного треугольника

Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.

Рассмотрим положение отрезка АВ относительно горизонтальной плоскости проекций π₁ (Рисунок 2.5).

Рисунок 2.5 – Определение истинной величины отрезка общего положения

АА₁ – расстояние от точки А до плоскости проекций π₁;

ВВ₁ – расстояние от точки В до плоскости проекций π₁;

ΔАКВ – прямоугольный треугольник, в котором:

ВК=ВВ₁–АА₁=Δ₁ – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π₁ (то есть, разности координат Z точек А и В);

АВ – гипотенуза ΔАКВ – истинная величина.

При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.

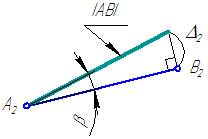
Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π₂

2.4. Точка и прямая

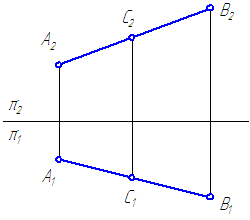
Если точка принадлежит прямой, то её проекции:

Рисунок 2.7 – Принадлежность точки прямой
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:

Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:

Упражнение

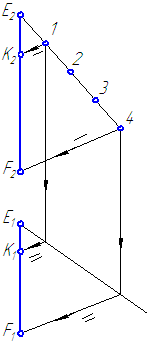
Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)

Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:

Упражнение

Определить принадлежность точки С отрезку прямой АВ (Рисунок 2.9).

Рисунок 2.9а – Решение упражнения 2. Способ 1.

Рисунок 2.9б – Решение упражнения 2. Способ 2.

Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.

2.5. Следы прямой

След прямой – точка пересечения прямой с плоскостью проекций.

Прямая общего положения в общем случае может быть три следа:

След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:

Рисунок 2.10 – Построение следов отрезка прямой АВ

Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).

Для построения горизонтального следа прямой АB необходимо:

Чтобы построить фронтальный след отрезка АB прямой, необходимо:

Ниже приводим алгоритм построения следов отрезка прямой АВ:

Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ

Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.

2.6. Взаимное расположение прямых

Две прямые в пространстве могут быть:

Параллельные прямые – прямые, пересекающиеся в несобственной точке.

Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).

Рисунок 2.12 – Параллельные прямые
Пересекающиеся прямые – прямые, имеющие одну общую точку.

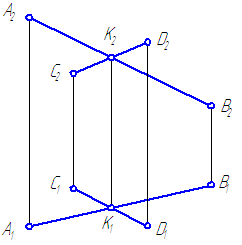
Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).

Рисунок 2.13 – Пересекающиеся прямые

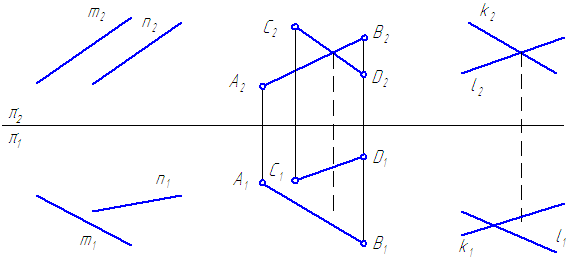
Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).

Рисунок 2.14 — Скрещивающиеся прямые

2.7. Проекции плоских углов

Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.

Рисунок 2.15

По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.

Теорема о проецировании прямого угла в частном случае

Рисунок 2.16 – Проецирование прямого угла

Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,

2.8. Задачи для самостоятельного решения

1. Построить отрезок прямой АВ // π₁, равный 35 мм и наклонённый к π₂ под углом 25° (Рисунок 2.17).

Рисунок 2.17

2. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π₂ и π₁.

3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π₁ и 45° — к плоскости проекций π₂.

4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π₂/π₁ (Рисунок 2.18).

Источник

Что такое прямая общего положения

Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.18).

Рисунок 18. Прямая общего положения

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня . В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.19). Для любой пары точек горизонтали должно быть справедливо равенство

Рисунок 19. Горизонтальная прямая

2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями ( рис.20).

Рисунок 20. Фронтальная прямая

2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 21).

Рисунок 21. Профильная прямая

Рисунок 22. Фронтально проецирующая прямая

4. Прямые параллельные биссекторным плоскостям (рис. 25)

5. Прямые перпендикулярные биссекторным плоскостям (рис. 25)

Источник

Что такое прямая общего положения

Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.

Рисунок 8

а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.

Рисунок 9

б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

Рисунок 10

Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.

Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

Рисунок 11

Рисунок 12.

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).

Рисунок 13

Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

а) три точки, не лежащие на одной прямой;

Рисунок 14

б) прямая и точка, не лежащая на ней;

Рисунок 15

в) две параллельные прямые;

Рисунок 16

г) две пересекающиеся прямые;

Рисунок 17

д) плоская фигура (многоугольник, круг и т.д.).

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Рисунок 18

Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.

Рисунок 19

Рисунок 20

1. Как образуется комплексный чертеж прямой линии?

2. Прямые какого положения вы знаете?

3. Назовите прямые уровня.

4. Как называется прямая, проекцией которой на горизонтальной плоскости будет точка?

5. Перечислите способы задания плоскости.

6. Дайте определение плоскости общего положения.

7. Какие бывают плоскости частного положения? Как они называются и как выглядят на комплексном чертеже?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник