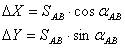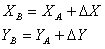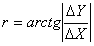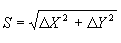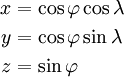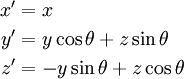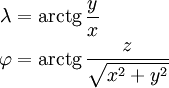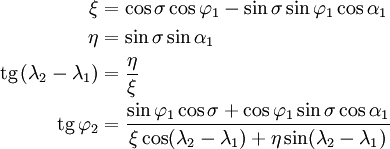что такое прямая геодезическая задача
Прямая и обратная геодез задачи



Геодезическая задача – математического вида задача, связаная с определением взаимного положения точек земной поверхности и подразделяется на прямую и обратную задачу.
Обратная геодезическая задача (ОГЗ) заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и дирекционного угла направления между этими точками.
В зависимости от длины геодезической линии, соединяющей рассматриваемые точки, применяются различные методы и формулы, разработанные в геодезии. По размерам принятого земного эллипсоида (см. Эллипсоид Красовского) составляются таблицы, облегчающие решение геодезических задач и рассчитанные на использование определённой системы формул.
Для определения координат точки в прямой геодезической задаче обычно применяют формулы:
1) нахождения приращений :
2) нахождения координат :
В обратной геодезической задаче находят дирекционный угол и расстояние:
1) вычисляют румб по формуле :
2) находят дирекционный угол в зависимости от четверти угла :
3) определяют расстояние между точками :
Геодезическая задача в том и другом виде возникает при обработке полигонометрии и триангуляции, а также во всех тех случаях, когда необходимо определить взаимное положение двух точек по длине и направлению соединяющей их линии или же расстояние и направление между этими точками по их геодезическим координатам. В ряде случаев геодезические задачи решают в пространственных прямоугольных координатах по формулам аналитической геометрии в пространстве. В этих случаях вместо длины и дирекционного угла, соединяющей две точки, используют длину и пространственные компоненты направления прямой линии между этими точками.
Тахетрическая съемка
Тахеометрическая съемка – топографическая съемка, выполняемая с помощью теодолита или тахеометра и дальномерной рейки (вехи с призмой), в результате которой получают план местности с изображением ситуации и рельефа.
Тахеометрическая съемка выполняется самостоятельно для создания планов или цифровых моделей небольших участков местности в крупных масштабах (1: 500 – 1: 5000) либо в сочетании с другими видами работ, когда выполнение стереотопографической или мензульной съемокэкономически нецелесообразно или технически затруднительно. Ее результаты используют при ведении земельного или городского кадастра, для планировки населенных пунктов, проектирования отводов земель, мелиоративных мероприятий и т.д. Особенно выгодно ее применение для съемки узких полос местности при изысканиях трасс каналов, железных и автомобильных дорог, линий электропередач, трубопроводов и других протяженных линейных объектов.
Слово «тахеометрия» в переводе с греческого означает «быстрое измерение». Быстрота измерений при тахеометрической съемке достигается тем, что положение снимаемой точки местности в плане и по высоте определяется одним наведением трубы прибора на рейку, установленную в этой точке. Тахеометрическая съемка выполняется обычно с помощью технических теодолитов или тахеометров.
При использовании технических теодолитов сущность тахеометрической съемки сводится к определению пространственных полярных координат точек местности и последующему нанесению этих точек на план. При этом горизонтальный угол B между начальным направлением и направлением на снимаемую точку измеряется с помощью горизонтального круга, вертикальный угол v – вертикального круга теодолита, а расстояние до точки D – дальномером. Таким образом, плановое положение снимаемых точек определяется полярным способом (координатами в,d), а превышения точек – методом тригонометрического нивелирования.
Преимущества тахеометрической съемки по сравнению с другими видами топографических съемок заключаются в том, что она может выполняться при неблагоприятных погодных условиях, а камеральные работы могут выполняться другим исполнителем вслед за производством полевых измерений, что позволяет сократить сроки составления плана снимаемой местности. Кроме того, сам процесс съемки может быть автоматизирован путем использования электронных тахеометров, а составление плана или ЦММ – производить на базе ЭВМ и графопостроителей. Основным недостатком тахеометрической съемки является то, что составление плана местности выполняется в камеральных условиях на основании только результатов полевых измерений и зарисовок. При этом нельзя своевременно выявить допущенные промахи путем сличения плана с местностью.
Что такое обратная и прямая геодезическая задача: суть, методы решения, назначение
В строительстве большую часть времени занимают геодезические работы. Это комплекс различных измерений и вычислений на местности. Стоит ли говорить, что качество выполненных работ зависит от точности полученных результатов. Это влияет на размещение зданий и сооружений, а также возведение их конструктивных элементов. Все должно соответствовать проектным показателям и техническим регламентам. Геодезические работы выполняются в объеме, определенном особенностями объекта и стадией его реализации. Компания «Промтерра» специализируется на их проведении с составлением необходимых чертежей, схем и расчетов. Для этого есть все составляющие: действующая лицензия, опыт, допуск СРО, штат специалистов. Один из вопросов, который поступает при выполнении работ, касается геодезической задачи. Что это такое, как используется в работе и ее назначение.
Математика в действии
По своей сути геодезические задачи — это математика в чистом виде. Основная задача состоит в определении взаимного положения точек принадлежащих какой-либо поверхности. Наиболее часто приходится иметь дело с прямыми и обратными геодезическими задачами, но на этом математические вычисления не заканчиваются. В зависимости от поставленных условий могут применяться и другие виды. Например, решение треугольника по измеренным углам и сторонам. Интересный исторический факт: с геодезическими задачами исследователи этой темы работают уже больше трех веков, а споры относительно методов дальше продолжаются.
Что такое прямая геодезическая задача
Эта разновидность предполагает вычисление координат, то есть широты и долготы определенной точки. А она, в свою очередь, лежит на математически правильной поверхности — земном эллипсоиде. Вычисления производятся по координатам другой точки, по длине и азимуту геодезической линии. Точность решения зависит от корректности исходных данных. Для проведения вычислений используют формулы нахождения приращений и определения координат.
Специалисты применяют разные методы для получения результатов. Наиболее востребованными считаются косвенный и прямой. Они отличаются тем, что в основе лежит точность исходных данных. Косвенные методы решения очень чувствительны к ним. Если в исходнике есть значительные расстояния, изменения по азимуту, то вычисления не получится сделать, или они будут с большими погрешностями. Прямые методы работают по соотношениям сфероидической геодезии, поэтому результаты можно получить более точные. Кстати, прямой тип геодезических задач применяется при вычислении координат в теодолитном ходе.
Что такое ОГЗ: суть обратной геодезической задачи
При работе над обратной геодезической задачей вычисления проводятся по известным координатам двух точек на земном эллипсоиде. Это нужно для получения значений горизонтального положения линий между ними, а также дирекционного угла этой самой линии. В этом состоит суть. Для получения искомых величин используется вычисление румба и расстояние между координатами точек. Нужно помнить, что дирекционный угол при этом находится по четверти системы координат, которая и является объектом, где размещены искомые позиции. Для решения нужно учитывать знаки приращения, которые свойственны для определенных четвертей. В этом типе задач уделяют большое значение сходимости результатов, поэтому расчеты могут проводиться несколько раз. На это влияют свойства горизонтального положения между точками. В каких случаях применяется обратная геодезическая задача? В тех, когда по известным двум точкам и их координатам определяют расстояние не только между ними, но и дирекционный угол линии.
В том или ином виде геодезические задачи возникают и в других направлениях — в полигонометрии, триангуляции, но на этом не заканчивается востребованность. Используется также, когда стоит задача определения взаимного положения точек по исходным данным длины и направления соединяющей линии. Есть ряд случаев, когда геодезические задачи решают с использованием формул аналитической геометрии в пространстве. Речь идет о пространственных прямоугольных координатах. Для этого используют пространственные компоненты направления прямой линии между этими точками.
Обратный тип геодезической задачи — не просто математическая проверка и вычисления. Она имеет практическое значение, ведь используется при вычислении длин проектных линий. Кроме этого, используется при выполнении привязки теодолитных ходов к пунктам геодезической сети, съемочных сетей и сетей сгущения. Еще одно практическое назначение — определение направления с пункта на пункт при отсутствии видимости. Обратная геодезическая задача используется в промышленном и гражданском строительстве.
А как решать обратные задачи, если в исходнике большие расстояния? В этом случае рекомендуется использовать метод итерации. Его можно использовать при расстояниях до 20 000 км. Итерация основана на решении прямой геодезической задачи любым выбранным методом — численным или аналитическим. И точность решения именно ОГЗ определяется решением ПГЗ.
Прямые и обратные геодезические задачи требуют получения точных результатов. Насколько получится достичь поставленной цели, зависит от исходных сведений и выбранного метода решения. Вычисление способом Бесселя, методом Рунге-Кутта-Фельберга, итерации, численного интегрирования — в каждом отдельном случае выбор зависит от расстояний и координат точек. В штате компании «Промтерра» работают опытные специалисты в сфере инженерной геодезии, поэтому за решение даже самых сложных задач можно быть спокойными. Тема геодезических задач всегда остается актуальной, поэтому отслеживание последних тенденций в проведении вычислений для получения точных результатов — необходимость. Важно отметить, что подобного плана математические методы востребованы не только в геодезической сфере деятельности, но и в навигации, корректировке ракетного огня и др.
Прямая геодезическая задача, решение на плоскости
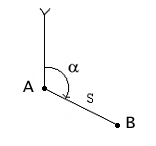
Прямая геодезическая задача состоит в том, что по известным координатам начального пункта А(хА,уА), линии АВ, дирекционному углу этой линии αАВ и ее горизонтальному проложению SАВ — вычисляют координаты конечной точки В(хВ, уВ). Прямая геодезическая задача решается разными способами.
Для точек на плоскости она решается следующим образом.
Разности ΔX и ΔY точек последующей и предыдущей называются приращениями. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:
Так как в этих формулах SAB всегда число положительное, то знаки приращений ΔX и ΔY зависят от знаков cos αAB и sin αAB. Для различных значений углов знаки ΔX и ΔY представлены в таблице ниже.
Таблица знаков приращений координат ΔX и ΔY
| Приращения | Четверть окружности в которую направлена линия | |||
| I (СВ) | II (ЮВ) | III (ЮЗ) | IV (СЗ) | |
| ΔX | + | – | – | + |
| ΔY | + | + | – | – |
При помощи румба, приращения вычисляют по формулам:
Знаки приращениям дают в зависимости от названия румба.
Вычислив приращения, находим искомые координаты другой точки:
Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения. Прямая геодезическая задача чаще всего используется при вычислении координат в теодолитном ходе.
Что такое прямая и обратная геодезическая задача?
Основной профиль компании БРИГС – геодезические работы в строительстве. Мы стараемся предоставлять информацию о нашей деятельности в как можно более доступной форме. Довольно часто нас спрашивают о геодезической задаче – что это, какими методами она решается и какие результаты приносит ее выполнение? На эти вопросы мы постараемся ответить в данном обзоре.
Что такое геодезическая задача?
Итак, геодезическая задача заключается в определении взаимного положения заданных точек на поверхности земли. В том или ином виде она возникает при обработке триангуляции и полигонометрии, то есть в процессе создания сети опорных пунктов геодезии. Геодезическая задача бывает прямой и обратной.
Прямая геодезическая задача решается методом вычисления широты и долготы конкретной точки, которая лежит на условном земном эллипсоиде. При этом необходимо знать координаты другой точки, а также длину и дирекционный угол направления, соединяющего обе эти позиции. Обратная геодезическая задача заключается в определении длины и дирекционного угла направления между точками на земном эллипсоиде с исходными геодезическими координатами.
Прямая геодезическая задача.
Решение задач данного типа проводится с помощью формул нахождения приращений и определения координат. Возможность и точность расчета координат точек зависит от корректности исходных данных, а также применяемой методики. Решение прямой геодезической задачи может осуществляться косвенными или прямыми методами.
Что касается первых, они являются весьма чувствительными к исходным данным и не работают при наличии значительных расстояний и изменений азимута, в частности, в северных широтах. Прямые же методы позволяют получить достаточно точные координаты по соотношениям сфероидической геодезии.
Обратная геодезическая задача.
В данном случае искомые величины рассчитываются с помощью вычисления румба и расстояния между заданными точками. При этом угол дирекции находится по четверти системы координат, в которой размещены искомые позиции.
Решение обратной геодезической задачи проводится с учетом знаков приращений. В свою очередь последние свойственны той или иной четверти. Правильность решения определяется сходимостью результатов вычислений, которые проводятся несколько раз в зависимости от свойств горизонтального проложения между расчетными точками.
GIS-LAB
Географические информационные системы и дистанционное зондирование
Задачи на сфере: прямая геодезическая задача
Прямая геодезическая задача — это нахождение положения точки по координатам исходного пункта и значениям начального направления и расстояния.
Содержание
[править] Общие положения
В качестве модели Земли принимается сфера с радиусом R, равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга.
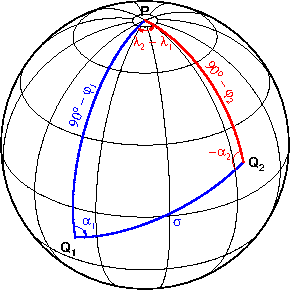
Введём следующие обозначения:
Линейное расстояние по дуге большого круга s связано со сферическим расстоянием σ формулой s = R σ.
Прямая и обратная геодезические задачи являются важными элементами более сложных геодезических задач.
[править] Постановка задачи
На рисунке синим цветом выделены заданные элементы сферического треугольника, красным цветом неизвестные.
[править] Алгоритм
Существует великое множество подходов к решению поставленной задачи. Рассмотрим простой и надёжный векторный метод.
Если третий пункт пропустить, на выходе вместо долготы λ₂ получится разность долгот (λ₂ − λ₁), что упростит алгоритм. Останется только прибавить долготу первого пункта. С другой строны, благодаря третьему пункту долгота λ₂ всегда будет в диапазоне [−180°, +180°].
Пример реализации алгоритма в виде функции языка Си:
Следует заметить, что прямая и обратная задача математически идентичны, и алгоритмы их решения зеркально отражают друг друга.
[править] Преобразование сферических координат в декартовы
В данном случае в качестве сферических координат φ, λ подставим углы (90° − σ), (180° − α₁).
[править] Вращение вокруг оси
Представим оператор вращения вокруг оси X на угол θ в следующем виде:
Операторы вращения вокруг осей Y и Z получаются перестановкой символов.
Реализация вращения вокруг i-ой координатной оси на Си:
[править] Преобразование декартовых координат в сферические
В данном случае в роли сферических координат φ, λ окажутся φ₂, λ₂.
[править] Пример программной реализации
Исходники вышеприведённых функций можно найти в архиве Sph.zip в файле sph.c. Кроме того, в файл sph.h включены следующие определения:
Теперь напишем программу, которая обращается к функции SphereDirect для решения прямой задачи:
В архиве Sph.zip этот код находится в файле dir.c. Создадим исполняемый модуль dir компилятором gcc:
Впрочем, в архиве есть Makefile. Для MS Windows готовую программу dir.exe можно найти в архиве Sph-win32.zip.
Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и « [править] Решение прямой задачи средствами PROJ
В пакет PROJ входит программа geod, предназначенная для решения прямых и обратных геодезических задач на сфере. Так выглядит команда обработки файла dir.dat:
Параметр +a определяет радиус сферы, -f — формат вывода угловых величин, +units — единица измерения расстояний. В итоге получим идентичный результат:
Различие значений α₂ на 360° объясняется тем, что dir выводит азимуты в диапазоне от 0° до 360°, а geod от −180° до +180°.
С помощью geod можно также расставить промежуточные точки вдоль геодезической линии либо по дуге малого круга на заданном расстоянии от исходного пункта. В обоих случаях нужно задать положение начальной точки параметрами +lat_1, +lon_1 и либо координаты второй точки +lat_2, +lon_1, либо расстояние и азимут ко второй точке +S, +A. За подробностями обращайтесь к документации.
[править] Альтернативные методы
Большая часть других методов основана на сферической тригонометрии. Многие из них используют вычисление φ₂ или (λ₂ − λ₁) по таким функциям, как синус, косинус или гаверсинус. Это приводит к неоднозначности результатов вблизи особых значений, когда производная функции равна нулю. Такие методы не могут считаться универсальными.
К наиболее надёжным относится следующий способ:
В сферической тригонометрии углы и стороны должны быть в диапазоне [0, 180°]. Алгоритмизация формул требует анализа и обработки случаев, когда входные величины не попадают в эти рамки.
[править] Ссылки
Последнее обновление: 2020-05-10 07:46
Дата создания: 11.03.2014
Автор(ы): ErnieBoyd