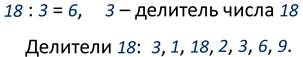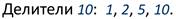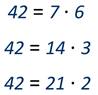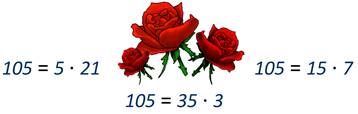что такое простые и составные числа видеоурок

Что такое простые и составные числа видеоурок

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

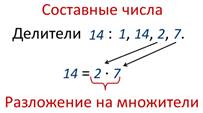
Вспомним, что такое делитель натурального числа. Делителем натурального числа а называют натуральное число, на которое а делится без остатка.

Рассмотрим натуральное число 5.

Например: числа 3,7,11,13 – простые.

Рассмотрим натуральное число 6.

Число 6 без остатка делится на 1,2,3,6. Значит, натуральное число 6 имеет четыре делителя. Такие числа называют составными. Натуральное число называют составным, если оно имеет более двух делителей.

Например: числа 4,8,9,10 – составные.

Заметим, что число 1 имеет только один делитель: само это число. Его не относят ни к составным, ни к простым числам.

Рассмотрим более подробно натуральное число 350.

350 мы можем представить в виде произведения двух множителей 35 и 10.

Числа 35 и 10 – составные. Их мы тоже можем представить в виде произведений:

Числа 2,5,7 являются простыми (каждое из них имеет только два делителя). Значит, число 350 мы представили в виде произведения простых чисел. Другими словами, число 350 мы разложили на простые множители.

Разложить натуральное число на простые множители – это значит представить его в виде произведения простых чисел.

Число 350 мы можем разложить на простые множители и другим способом:

350 = 70 · 5 = 10 · 7 · 5 = 2 · 5 · 7 · 5

Мы получили те же самые простые множители, только записаны они в другом порядке.

Т. о., всякое составное число можно разложить на простые множители. При любом способе разложения получаются одни и те же множители.

Источник

Урок 4 Бесплатно Простые и составные числа

На этом уроке мы познакомимся с двумя видами чисел. Они будут различаться количеством делителей.

Также узнаем, как можно разложить составное число на простые числа, изучим основную теорему арифметики и увидим решето Эратосфена.

Простые и составные числа

Если мы попытаемся разделить число 11 на какие-нибудь числа без остатка, то у нас получится это сделать, только если мы будем делить на 1 или на 11.

Получается, что число 11 имеет только два делителя: 1 и 11.

Если мы поступим так же с числами 9 и 18, то узнаем, что у числа 9 три делителя: 1, 3 и 9, а число 18 имеет шесть делителей: 1, 2, 3, 6, 9 и 18

Натуральное число простое, если оно имеет делителями только единицу и само себя.

Если натуральное число имеет больше двух делителей, то оно называется составным.

Таким образом, числа, которые мы используем при счете, в итоге можно разделить на три разные группы по количеству делителей:

Пример 1

Даны числа: 1, 7, 10, 12, 13, 24. Найдите все делители для каждого из чисел. Выпишите числа, имеющие:

В) больше двух делителей

Решение:

Число 1 имеет один делитель: 1

Число 7 имеет два делителя: 1, 7

Число 10 имеет четыре делителя: 1, 2, 5, 10

Число 12 имеет шесть делителей: 1, 2, 3, 4, 6, 12

Число 13 имеет два делителя: 1, 13

Число 24 имеет восемь делителей: 1, 2, 3, 4, 6, 8, 12, 24

Ответ:

А) один делитель- 1

Б) два делителя- 7, 13

В) больше двух делителей- 10, 12, 24

Таким образом, числа 7 и 13 являются простыми, потому что имеют по два делителя.

Числа 10, 12, 24 являются составными, потому что имеют больше двух делителей.

Пример 2

Даны числа: 2, 4, 17, 21, 28, 30, 42, 55, 127. Какие из них простые, а какие составные?

Найдите все делители для составных чисел.

Решение:

Простые: 2, 17, 127

Составные: 4, 21, 28, 30, 42, 55

Число 4 имеет три делителя: 1, 2, 4

Число 21 имеет четыре делителя: 1, 3, 7, 21

Число 28 имеет шесть делителей: 1, 2, 4, 7, 14, 28

Число 30 имеет восемь делителей: 1, 2, 3, 5, 6, 10, 15, 30

Число 42 имеет восемь делителей: 1, 2, 3, 6, 7, 14, 21, 42

Число 55 имеет четыре делителя: 1, 5, 11, 55

У меня есть дополнительная информация к этой части урока!

Простые и составные числа с древнейших времён интересовали разных учёных. Например, древнегреческий учёный Эратосфен (276- 194 гг. до н.э.) занимался вопросом таких чисел.

Он был главой Александрийской библиотеки и в его работах появились первые факты математической географии, вычисления величины земного шара с достаточно для того времени хорошей точностью.

Для своих вычислений он создал довольно простой способ, который использовался для исследования простых чисел и дошел до нашего времени без изменений. Этот способ назвали «Решето Эратосфена».

Пусть перед нами стоит задача нахождения простых чисел от 1 до 100 включительно.

Распишем все эти числа в квадрате 10 на 10.

После этого начинаем зачеркивать те, которые делятся на 2, потом на 3, потом на 5 (на 4 не берем, ведь они уже будут зачёркнуты, когда мы будем зачеркивать делящиеся на 2), потом на 7 и… всё!

Больше зачеркивать ничего не нужно, так как дальше работает доказанное правило: оставшиеся числа в таблице будут простыми.

Почему вдруг такую таблицу назвали решетом?

Получается вот что: мы убираем числа, потом повторяем с оставшимися числами, и то, что будет не зачёркнуто, как бы напоминает то, что ОСТАЕТСЯ В РЕШЕТЕ.

Если внимательно посмотреть на табличку, то можно увидеть что все вычеркнутые стоят на прямых линиях. А, кто видел решето, тот знает, что оно состоит из нитей, натянутых в виде прямых. Значит, можно построить такое решето, просто проводя прямую в тех местах, где число нужно вычеркнуть – вот и все. Поэтому мы и получаем подобие решета.

Решето Эратосфена работает по подобию простой вычислительной машины. И значит, еще очень давно, была изобретена СЧЕТНАЯ МАШИНА.

На сегодняшний день не существует формулы получения любого простого числа, зато еще с древности известно решето Эратосфена. Всё гениальное просто, как говорится в известном афоризме.

На числовой прямой простые числа не имеют никакой закономерности, стоят в хаотичном порядке. Но если мы соберем числовую прямую в решето Эратосфена большого размера, мы их все просеем через него и соберем без исключения и потерь.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Простые и составные числа

Урок 4. Математика 6 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Простые и составные числа»

Число 18 делится на 3 без остатка, так как 18 : 3 = 6. Говорят, что 3 – делитель числа 18. Это число имеет и другие делители. Найдём все натуральные числа, на которые делится 18 без остатка, то есть найдём все делители восемнадцати.

Число 10 имеет четыре делителя:

А есть числа, которые имеют только два делителя.

Такие числа называют простыми числами.

Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.

А вот числа, имеющие и другие делители, называют составными.

Число 1 имеет только один делитель: само это число. Поэтому его не относят ни к составным, ни к простым числам.

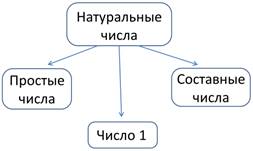
В зависимости от количества делителей, все числа можно разбить на

Если натуральное число имеет только два делителя, то его называют простым.

Если натуральное число имеет более двух делителей, то его называют составным.

Если натуральное число имеет только один делитель – это единица.

Поговорим подробнее о простых числах.

Число 2 – наименьшее простое число. Кроме того, 2 – единственное ЧЁТНОЕ простое число. Остальные простые числа нечётные.

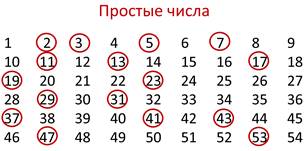
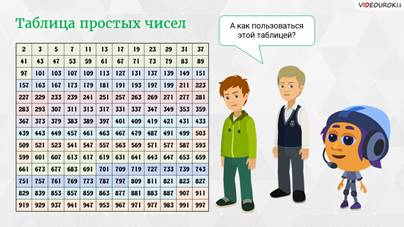
Математики составили специальные таблицы, в которых перечисляются подряд все простые числа.

Из этой таблицы желательно знать наизусть однозначные и двузначные простые числа, что упростит вычисления по многим темам школьной программы.

Обратите внимание, что простые числа в ряду натуральных чисел встречаются неравномерно, и чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует ли последнее простое число? Оказывается, что ответ на этот вопрос уже есть и найден…больше 2000 лет назад.

Великий математик Древней Греции Евклид доказал, что полный список составить просто невозможно. Можно сказать также, что среди простых чисел нет самого большого числа. Так две с лишним тысяч лет назад Евклид лишил математиков надежды получить полный список простых чисел.

Теперь поговорим подробнее о составных числах.

Любое составное число можно разложить на 2 множителя, каждый из которых больше одного.

Для поздравления приобрели 105 роз, из которых были сделаны букеты. Найдите возможные варианты числа одинаковых букетов и количество роз в каждом. Известно, что букетов было больше одного. Кроме того, в каждом букете было больше одной розы.

В зависимости от того, сколько делителей имеет число, числа делятся на простые и составные. Не забудем про единицу, которая не является ни простым, ни составным числом.

Знание наизусть однозначных и двузначных простых чисел или проверка их по таблице вам понадобится для сокращения дробей, нахождения наибольшего общего кратного, наименьшего общего знаменателя и в других вычислениях.

Источник

Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена

В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.

Простые и составные числа – определения и примеры

Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.

Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.

Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.

Простые числа – это натуральные числа, имеющие только два положительных делителя.

Составное число – это натуральное число, имеющее более двух положительных делителей.

Натуральные числа, которые не являются простыми, называют составными.

Таблица простых чисел

Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:

Рассмотрим теорему, которая объясняет последнее утверждение.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Простых чисел бесконечно много.

Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.

Решето Эратосфена

Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.

Перейдем к формулировке теоремы.

Данное число простое или составное?

Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.

Доказать что число 898989898989898989 является составным.

Ответ: 11723 является составным числом.

Источник

Простые и составные числа

Урок 4. Математика 6 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Простые и составные числа»

Представим себе такую историю…

– Саша, давай с тобой сыграем в одну игру, – предложил другу Паша.

– Что за игра? – решил уточнить Саша.

– В общем, смотри: перед тобой таблица, в которой записан ряд натуральных чисел начиная с 2 и заканчивая 100, – начал Паша. – Тебе нужно взять число, а потом вычёркивать все числа, которые на него делятся. Вот, например, возьмём число 2, обведём его в кружочек, чтобы не потерять, и вычеркнем из этой таблицы все числа кратные двум.

– Понятно – прошептал Саша. – Значит, вычёркиваю все чётные числа.

– Хорошо! – продолжил Паша. — Следующее незачёркнутое число – 3. Обведём его в кружок. А теперь из оставшихся чисел тебе нужно вычеркнуть все числа кратные 3.

– Так… – начал размышлять Саша. — Если сумма цифр числа делится нацело на 3, то и само число делится нацело на 3.

И Саша принялся вычёркивать числа.

– Молодец! – поддержал друга Паша. – Следующее незачёркнутое число – 5. Значит, из оставшихся чисел тебе нужно вычеркнуть все числа кратные 5.

– Ага! Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5 – сказал Саша. И занялся вычёркиванием чисел.

– Отлично! – сказал Паша. – Перейдём к следующему незачёркнутому числу. И это 7. То есть теперь ты должен вычеркнуть из оставшихся чисел все числа кратные 7.

– Ну, признака делимости на 7 мы ещё не знаем, – задумался Саша, – значит, буду просто вычёркивать все числа, которые делятся на 7.

И Саша принялся вычёркивать числа.

– Ну вот и всё! – сказал Паша. – Наша игра окончена. Посмотри, в таблице у тебя остались только числа, которые делятся на 1 и сами на себя.

– И точно! – заметил Саша.

– То, что мы сейчас с тобой делали, называют «решето Эратосфена», – продолжил Паша.

– А почему решето? – спросил Саша. – Разве эта таблица с дырочками?

– Название «решето» метод получил потому, что, согласно легенде, Эратосфен (это древнегреческий математик) писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны числа, имеющие больше двух делителей. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все числа, имеющие больше двух делителей, а оставались только простые числа. Эратосфен дал таблицу простых чисел до 1000.

– А что это за простые числа? – спросил Саша.

– Давай спросим у Мудряша, – предложил Паша. – Он точно сможет нам помочь.

– Ребята, прежде чем я вас познакомлю с простыми числами, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. — Как вы уже знаете, все натуральные числа имеют делители. И вы, кстати, уже научились их находить с помощью свойств и признаков делимости. Меньше всего делителей у числа 1. Единственным его делителем является само это число. А вот любое другое натуральное число а имеет по крайней мере два делителя – 1 и само число а.

– А ведь действительно, – сказали мальчишки, – если число а разделить на 1, то получится а, а если число а разделить на а, то получится 1.

– Некоторые натуральные числа имеют ровно два делителя, – продолжил Мудряш. – Например, число 13 делится только на 1 и на 13. Другие же числа могут иметь больше двух делителей. Например, числа 6 и 18. Число 6 имеет четыре делителя: 1, 2, 3 и 6. А вот число 18 – шесть делителей: 1, 2, 3, 6, 9 и 18.

– Запомните! – сказал Мудряш. – Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число. Натуральное число называют составным, если оно имеет больше двух натуральных делителей.

– Может, вы сможете привести примеры простых и составных чисел? – спросил Мудряш у ребят.

– Простыми числами являются, – начали мальчишки, – 2, 3, 5, 7, 11, 13, 17, 19 и так далее. А составными числами будут: 8, 12, 16 и так далее.

– Молодцы! – похвалил ребят Мудряш. — Обратите внимание: число 2 – это наименьшее простое число. Кстати, это единственное чётное простое число. Потому что любое другое чётное число имеет по крайней мере три делителя: число 1, число 2 и само число. Простых чисел бесконечно много. Наибольшего простого числа не существует.

– Таким образом, – продолжил Мудряш, – все натуральные числа, в зависимости от количества делителей, можно разбить на три группы: 1 (один делитель), простые числа (два делителя) и составные числа (три и более делителей).

– А как узнать, глядя на число, простое оно или составное? – спросили мальчишки.

– Хороший вопрос! – обрадовался Мудряш. – Если число небольшое, то можно перебрать одно за другим все числа, которые могут быть его делителями. Например, возьмём число 11. Его делители могут встретиться лишь среди чисел от 1 до 11. Понятно, что 1 и 11 – делители числа 11. А перебирая одно за другим числа от 2 до 10, мы убедимся, что ни на одно из них число 11 не делится. Так что у числа 1 только два делителя. Значит, оно простое.

– А если число большое? – решили уточнить мальчишки.

– Если число большое, то понятно, что перебирать числа в поисках его делителей придётся слишком долго, – начал Мудряш. – А чтобы не тратить время на эту однообразную работу, пользуются таблицей простых чисел. На экране вы как раз и видите её.

– А как пользоваться этой таблицей? – спросили ребята.

– Здесь нет ничего сложного, – ответил Мудряш. — Вы должны просто посмотреть, есть в таблице интересующее вас число или нет. Если его в таблице нет – значит, оно составное. Конечно, учить эту таблицу наизусть не стоит. Но если вы запомните хотя бы все однозначные и двузначные простые числа, то это значительно упростит вычисления по многим темам школьной программы.

– Интересно, что последовательность простых чисел имеет много необычных свойств и тайн. Так, например, учёные Древней Эллады отметили, что среди простых чисел много таких, разность которых равна двум, например: 3 и 5, 5 и 7, 11 и 13, 17 и 19 и так далее. Подобные пары чисел называют простыми числами близнецами.

– А для чего вообще нужны простые числа? – спросили ребята.

– Простые числа помогают в поиске делителей, – начал Мудряш. — Так, например, возьмём число 510. Понятно, что оно составное, то есть имеет более двух делителей. Если мы представим это число в виде суммы разрядных слагаемых, то заметим, что оно не делится на 7. А значит, уже не нужно проверять его делимость ни на 14, ни на 21, ни на 28 и так далее.

– Запомните! – сказал Мудряш. – Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.

– А как это делают? – спросили ребята.

– Число 110 можно разложить в произведение чисел не равных единице. Например, 110 равно произведению 10 и 11. В свою очередь, число 10 тоже составное число. Значит, его тоже можно разложить в произведение, то есть 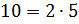. А тогда число 110 можно представить в виде произведения 2, 5 и 11. Обратите внимание: в правой части равенства все множители – простые числа. То есть мы с вами сейчас записали число 110 в виде произведения простых чисел. Говорят, что число 110 разложили на простые множители.

– Запомните! Разложить натуральное число на простые множители – значит представить его в виде произведения простых множителей.

– При разложении числа на простые множители удобно пользоваться схемой, – продолжил Мудряш. — Давайте я вам покажу эту схему на примере разложения числа 2940.

– Итак, 2940 — чётное число, значит, оно делится на 2. При делении получим 1470. Число 1470 также чётное. Значит, можем поделить его на 2. Получим 735. Заметим, что сумма цифр числа 735 равна 15. Значит, это число делится на 3. Разделим его. Получим 245. Число 245 оканчивается цифрой 5. Значит, оно делится на 5. Разделим. Получим 49. В свою очередь, число 49 делится на 7. Число 7 также делится на 7. И в результате получим 1.

– Обратите внимание: числа, расположенные друг под другом слева от вертикальной черты, получаются при последовательном делении на простые числа, записанные справа от черты.

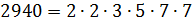
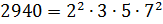
– Теперь можем записать число 2940 в виде произведения простых множителей. . Заметим, что в разложении числа присутствуют одинаковые множители — это две 2 и две 7. Как правило, одинаковые множители заменяют их степенями. Тогда .

– А все составные числа можно разложить на простые множители или есть исключения? – спросили мальчишки.

– Любое составное число можно разложить на простые множители, – ответил Мудряш. – При этом каждое число имеет своё, единственное разложение на простые множители, если не учитывать, в каком порядке они записаны. Утверждение о единственности разложения на простые множители называют основной теоремой арифметики.

А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним задание.

Итак, заполните таблицу. Если значение выражения — простое число, то во втором столбце таблицы поставьте знак «галочка», если составное – то в третьем столбце.

Решение: первое числовое выражение — сумма двух частных: 14 и 2, и 32 и 8. Первое частное равно 7, второе – 4. Тогда сумма равна 11. Число 11 – это простое число.

Следующее выражение: разность числа 25 и суммы частного чисел 6 и 2, и произведения 2 и 5. Частное равно 3, произведение – 10. Тогда сумма равна 13. Осталось вычислить разность. 25 минус 13 равно 12. Число 12 составное.

И последнее выражение: произведение суммы чисел 45 и 28, и разности числа 22 и произведения 3 и 7. Сумма равна 73. Произведение 3 и 7 равно 21. А разность 22 и 21 равна 1. Тогда произведение 73 и 1 равно 73. Число 73 простое.

Источник