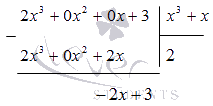что такое простой множитель дроби

Что такое множитель и разложение на простые множители

Дадим определение понятию «множитель» и разберемся что такое множитель. Какие множители бывают и почему некоторые из множителей — простые.

Определение множителя

В младших классах вы учили, что множители — это числа, которые мы умножаем, называя результат их умножения произведением.

Определения множителя как компонента умножения

Сейчас немного расширим понятие множителя.

Давайте рассмотрим определение множителя на примерах. Давайте определим где в представлении числа или выражения прячется множитель?

Пример 1

Пусть нам дано число 15. Это число можно представить в виде произведения . Значит, согласно определению 5 — это множитель, 3 — это тоже множитель.

Пример 2

Рассмотрим теперь выражение: . Это выражение можно представить в виде произведения . Получаем два множителя — первый множитель (2x-3) и второй множитель (2x+3).

Самое простое произведение имеет два множителя, но может быть и больше множителей.

Простые множители

Пример 1

Разложите число 65 на простые множители.

Решение: число 65 будем делить на простые числа, пока оно нацело не разделится. Так мы видим, что число 65 не делится на 2, 3 и 4, так как не соответствует признакам делимости на эти числа. Зато делится на 5, так как оканчивается на 5. При делении мы получаем 13. Число 13 — простое, так как делится только на себя и на единицу. Таким образом, число . И мы выполнили разложение числа на простые множители. Теперь вы знаете, как разложить число на простые множители.

Пример 2

Разложите число 270 на простые множители.

Решение: Разделим сначала число 270 на 2 (сначала берем самое маленькое простое число), получим 135. Посмотрим, делится ли это число на 3. Для этого сложим все числа, стоящие в разрядах данного числа — . Девять делится на 3, значит, и число 135 разделится на 3: . Получившееся число опять делится на 3: . И снова число 15 делится на 3: . Получили простое число 5. Делим .

Итак, запишем разложение числа 270 на простые множители в виде столбца, где справа от черты мы пишем на какое простое число мы делим, а слева — что получаем:

Разложение числа на простые множители в столбик.

Разложение числа на простые множители в строчку записывается так: .

Про разложение многочлена на множители поговорим в отдельной теме.

Источник

Метод неопределённых коэффициентов для разложения дроби на сумму простейших дробей

Простейшие дроби

$x^2+7x+30$ – не раскладывается.

Обобщая, получаем следующее определение:

Простейшими (элементарными) дробями называют дроби вида:

Примеры простейших дробей:

Любая рациональная алгебраическая дробь может быть разложена на сумму простейших дробей, и притом единственным способом.

Алгоритм разложения дроби на сумму простейших дробей

Попробуем её разложить на две простейшие дроби следующим образом:

Дроби равны, знаменатели равны, значит, должны быть равны и числители:

4 x+ 1 = A(x-3)+B(x+10) = (A+B) x+ (-3A+10B)

Теперь используем важнейшее свойство многочленов:

У равных многочленов коэффициенты при соответствующих степенях переменной равны.

Получаем представление дроби в виде суммы простейших дробей:

Этот способ разложения был предложен в 17 веке Декартом и получил название «метода неопределённых коэффициентов».

Алгоритм метода неопределённых коэффициентов

Примеры

Пример 1. Разложите на простейшие дроби:

Раскладываем знаменатель на множители:$ x^2+5x+6 = (x+2)(x+3)$

Записываем разложение с неопределенными коэффициентами:

Приравниваем коэффициенты при одинаковых степенях x:

Записываем разложение с неопределенными коэффициентами:

Записываем разложение с неопределенными коэффициентами:

Раскладываем знаменатель на множители:$ 9x^2-4 = (3x-2)(3x+2)$

Записываем разложение с неопределенными коэффициентами:

Пример 2*. Разложите на простейшие дроби:

Источник

Обыкновенные дроби

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

Виды дробей:

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Полученные числа запишем справа сверху над числителем.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

Источник

Разложение дроби на простейшие

Для закрепления материала будут рассмотрены несколько примеров и рассмотрена теория по разложению дробей на простейшие. Подробно рассмотрим метод неопределенных коэффициентов и метод частных значений, изучим всевозможные комбинации.

Простые дроби имеют название элементарных дробей.

Типы дробей

При упрощении выражения быстрее выполняются вычислительные функции. Представление дробно-рациональной дроби как суммы простейших дробей аналогично. Для этого применяют ряды Лорана для того, чтобы разложить в степенные ряды или для поиска интегралов.

Когда степень числителя многочлена меньше степени многочлена в знаменателе, имеет место разложение на простейшие дроби. Иначе применяется деление для выделения целой части, после чего производят разложение дробно-рациональной функции.

Применим деление углом. Получаем, что

Отсюда следует, что дробь примет вид

Алгоритм метода неопределенных коэффициентов

Для того, чтобы правильно произвести разложение, необходимо придерживаться нескольких пунктов:

Рассмотрим на нескольких примерах:

P 4 x + Q 4 ( x 2 + p x + q ) 4 + P 3 x + Q 3 ( x 2 + p x + q ) 3 + P 2 x + Q 2 ( x 2 + p x + q ) 2 + P 1 x + Q 1 x 2 + p x + q + + R 2 x + S 2 ( x 2 + r x + s ) 2 + R 1 x + S 1 x 2 + r x + s

Приведение полученной суммы простейших дробей при наличии неопределенного коэффициента к общему знаменателю, применяем метода группировки при одинаковых степенях х и получаем, что

Необходимо постоянно выполнять проверки. Это способствует тому, что приведение к общему знаменателю получит вид

Методом неопределенных коэффициентов считают метод разложения дроби на другие простейшие.

Использование метода частных значений способствует представлению линейных множителей таким образом:

По условию имеем, что степень многочлена числителя меньше степени многочлена знаменателя, тогда деление выполнять не нужно. Необходимо перейти к разложению на множители. для начала необходимо выполнить вынесение х за скобки. Получим, что

x 1 + x 2 = 5 x 1 · x 2 = 6 ⇔ x 1 = 3 x 2 = 2

Имея такой знаменатель, дробь раскладываем на простейшие дроби с неопределенными коэффициентами. Выражение примет вид:

Полученный результат необходимо приводить к общему знаменателю. Тогда получаем:

После упрощения придем к неравенству вида

Метод коэффициентов и метод частных значений отличаются только способом нахождения неизвестных. Данные методы могут быть совмещены для быстрого упрощения выражения.

По условию имеем, что степень числителя многочлена меньше знаменателя, значит зазложение примет вид

Производим приведение к общему знаменателю. Имеем, что

Приравняем числители и получим, что

157 = 8 C 3 ⇒ C 3 = 157 8

Поэтому подставим полученный значения в числитель, тогда

Раскроем скобки для того, чтобы привести подобные слагаемые с одинаковыми степенями. Придем к выражению вида

Итог решения – это искомое разложение дроби на простейшие вида:

При непосредственном применении метода неопределенных коэффициентов необходимо было бы решать все пять линейных уравнений, объединенных в систему. Такой метод упрощает поиск значения переменных и дальнейшее решение в совокупности. Иногда применяется несколько методов. Это необходимо для быстрого упрощения всего выражения и поиска результата.

Источник

Разложение дроби на простейшие.

Для начала разберем теорию, далее решим парочку примеров для закрепления материала по разложению дробно рациональной функции на сумму простейших дробей. Подробно остановимся на методе неопределенных коэффициентов и методе частных значений, а также на их комбинации.

Простейшие дроби часто называют элементарыми дробями.

Различают следующие виды простейших дробей:

Называют их соответственно дробями первого, второго, третьего и четвертого типов.

Для чего вообще дробь раскладывать на простейшие?

Приведем математическую аналогию. Часто приходится заниматься упрощением вида выражения, чтобы можно было проводить какие-то действия с ним. Так вот, представление дробно рациональной функции в виде суммы простейших дробей примерно то же самое. Применяется для разложения функций в степенные ряды, ряды Лорана и, конечно же, для нахождения интегралов.

К примеру, требуетя взять интеграл от дробно рациональной функции . После разложения подынтегральной функции на простейшие дроби, все сводится к достаточно простым интегралам

Но об интегралах в другом разделе.

Разложить дробь на простейшие.

Вообще отношение многочленов раскладывают на простейшие дроби, если степень многочлена числителя меньше степени многочлена в знаменателе. В противном случае сначала проводят деление многочлена числителя на многочлен знаменателя, а уже затем проводят разложение правильной дробно рациональной функции.

Выполним деление столбиком (уголком):

Следовательно, исходная дробь примет вид:

Таким образом, на простейшие дроби будем раскладывать

Алгоритм метода неопределенных коэффициентов.

Во-первых, раскладываем знаменатель на множители.

Здесь все методы хороши – от вынесения за скобки, применения формул сокращенного умножения, до подбора корня и последующего деления столбиком (при знаменателе в виде многочлена с рациональными коэффициентами степени выше второй). Об этом подробнее в разделе теории – разложение многочлена на множители.

В нашем примере все просто – выносим х за скобки.

Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами.

Здесь стоит рассмотреть виды выражений, которые могут быть у Вас в знаменателе.

Возьмите на заметку: какая степень – столько и слагаемых.

ОБЫЧНО ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ (как правило, довольно простая).

Если собрать все в кучу ,то дробь представится в виде суммы простейших дробей всех четырех типов:

Хватит теории, на практике все равно понятнее.

То есть, пришли к равенству:

При x отличных от нуля это равенство сводится к равенству двух многочленов

А два многочлена являются равными тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают.

При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных:

В-пятых, решаем полученную систему уравнений любым способом (при необходимости смотрите статью решение систем линейных алгебраических уравнений, методы решения, примеры), который нравится Вам, находим неопределенные коэффициенты.

В-шестых, записываем ответ.

Пожалуйста, не ленитесь, проверяйте ответ, приводя к общему знаменателю полученное разложение.

Метод неопределенных коэффициентов является универсальным способом при разложении дроби на простейшие.

Очень удобно использовать метод частных значений, если знаменатель представляет собой произведение линейных множителей, то есть имеет вид схожий с

Рассмотрим на примере, чтобы показать плюсы этого метода.

Разложить дробь на простейшие.

Так как степень многочлена в числителе меньше степени многочлена в знаменателе, то производить деление нам не придется. Переходим к разложению знаменателя на множители.

Для начала выносим х за скобки.

Находим корни квадратного трехчлена (например, по теореме Виета):

Следовательно, квадратный трехчлен можно записать как

То есть, знаменатель примет вид

При данном знаменателе, исходная дробь раскладывается в сумму трех простейших дробей первого типа с неопределенными коэффициентами:

Таким образом, пришли к равенству:

При х=0 имеем:

При х=2 имеем:

При х=3 имеем:

Как видите, различие метода неопределенных коэффициентов и метода частных значений лишь в способе нахождения неизвестных. Эти методы можно совмещать для упрощения вычислений.

Разложить дробно рациональное выражение на простейшие дроби.

Так как степень многочлена числителя меньше степени многочлена знаменателя и знаменатель уже разложен на множители, то исходное выражение представится в виде суммы простейших дробей следующего вида:

Приводим к общему знаменателю:

Приравниваем числители.

При х=1 имеем:

При х=-1 имеем:

При х=3 имеем:

Осталось найти неизвестные и

Для этого подставляем найденные значения в равенство числителей:

После раскрытия скобок и приведения подобных слагаемых при одинаковых степенях х приходим к равенству двух многочленов:

Приравниваем соответствующие коэффициенты при одинаковых степенях, тем самым составляем систему уравнений для нахождения оставшихся неизвестных и . Получаем систему из пяти уравнений с двумя неизвестными:

Из первого уравнения сразу находим , из второго уравнения

В итоге получаем разложение на простейшие дроби:

Если бы мы сразу решили применить метод неопределенных коэффициентов, то пришлось бы решать систему пяти линейных алгебраических уравнений с пятью неизвестными. Применение метода частных значений позволило легко отыскать значения трех неизвестных из пяти, что значительно упростило дальнейшее решение.

Источник