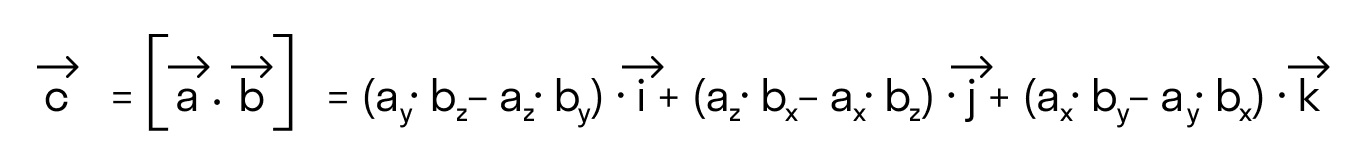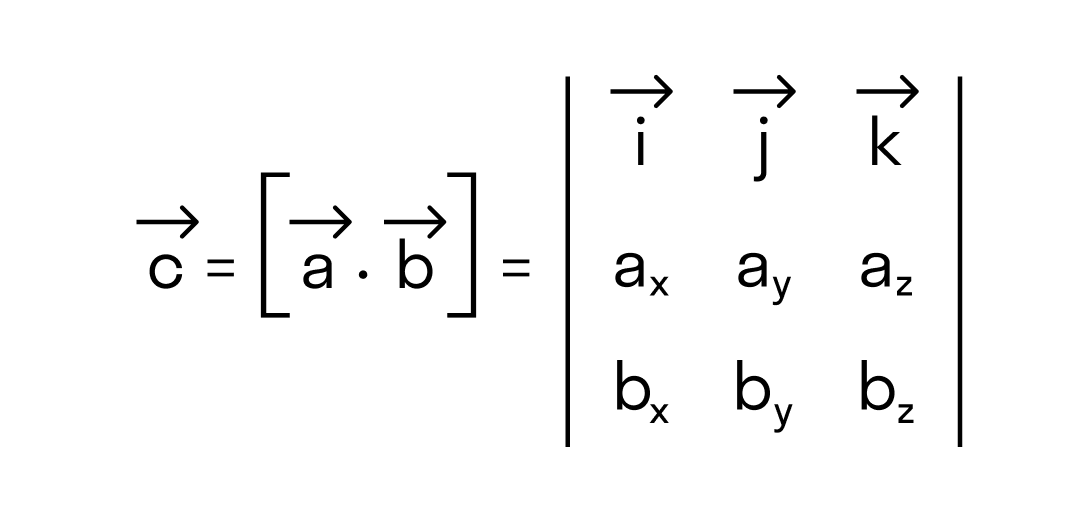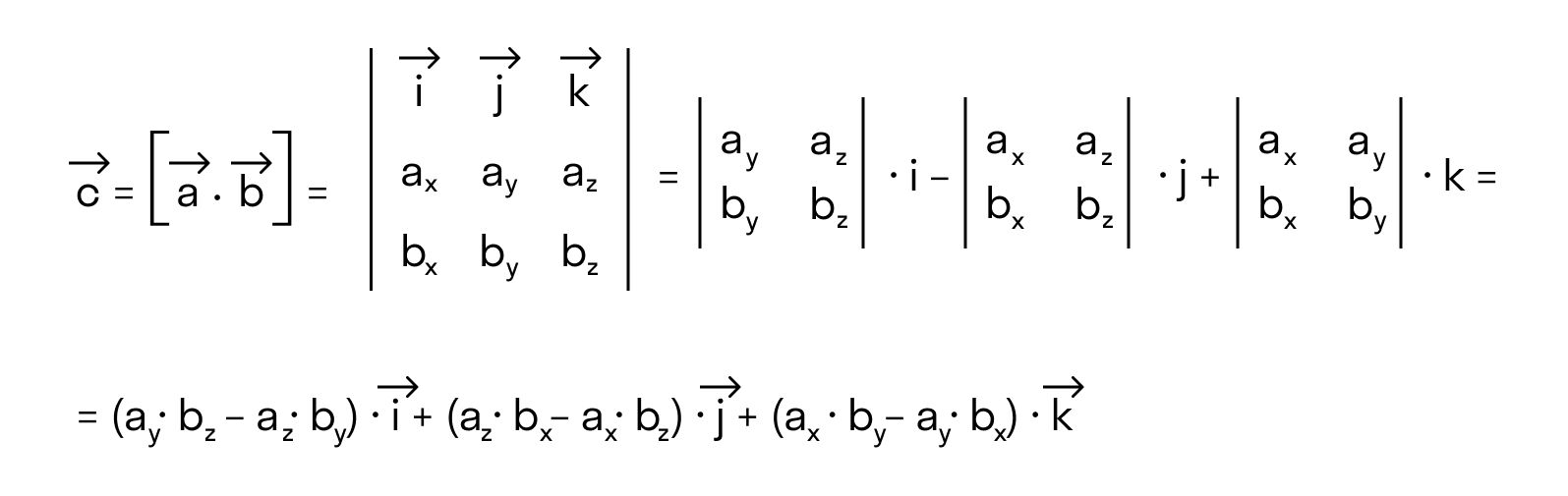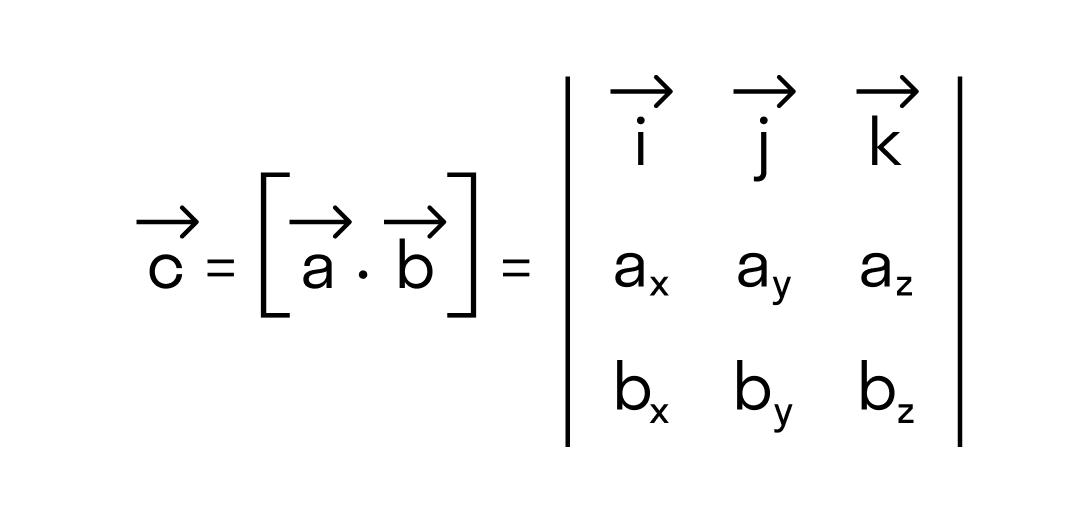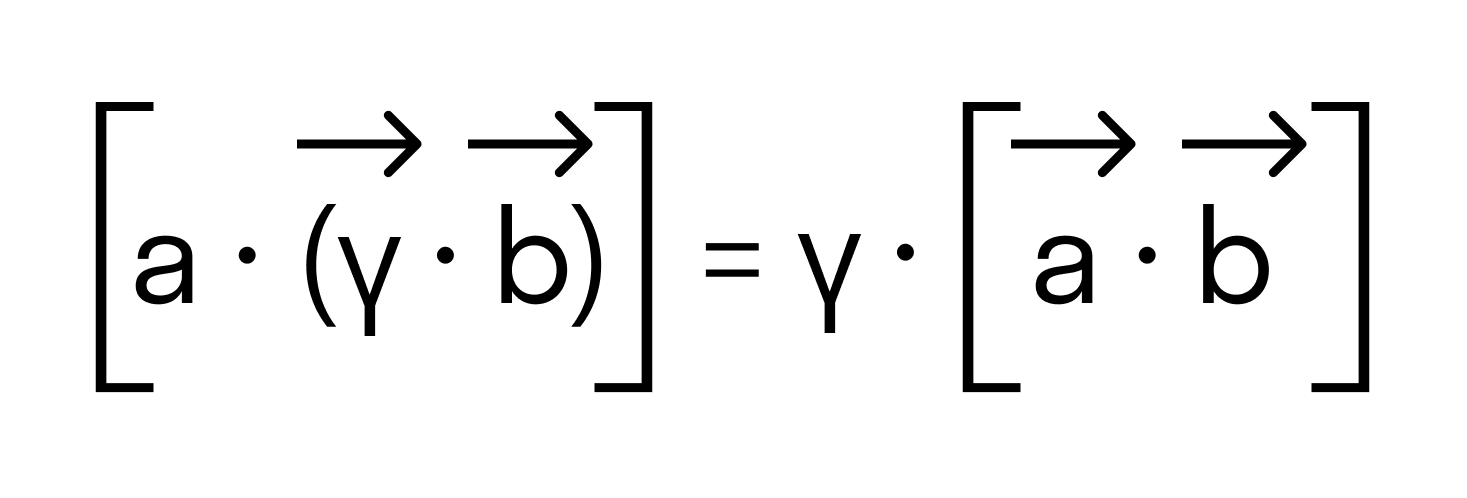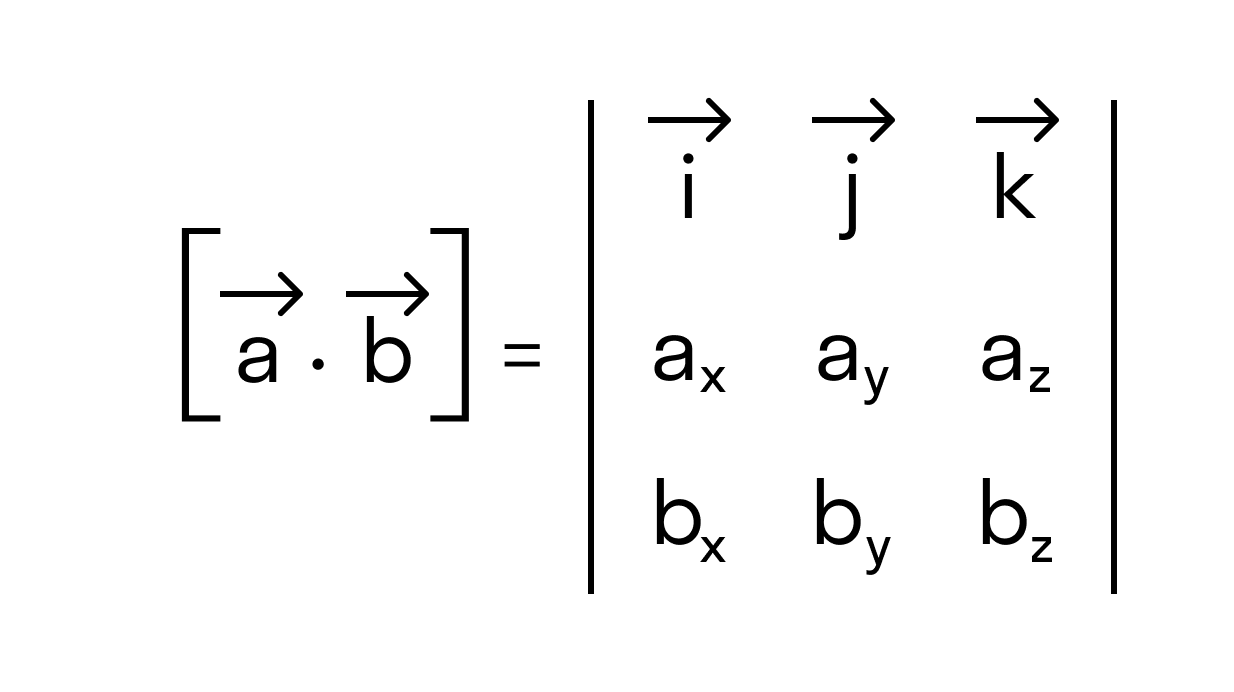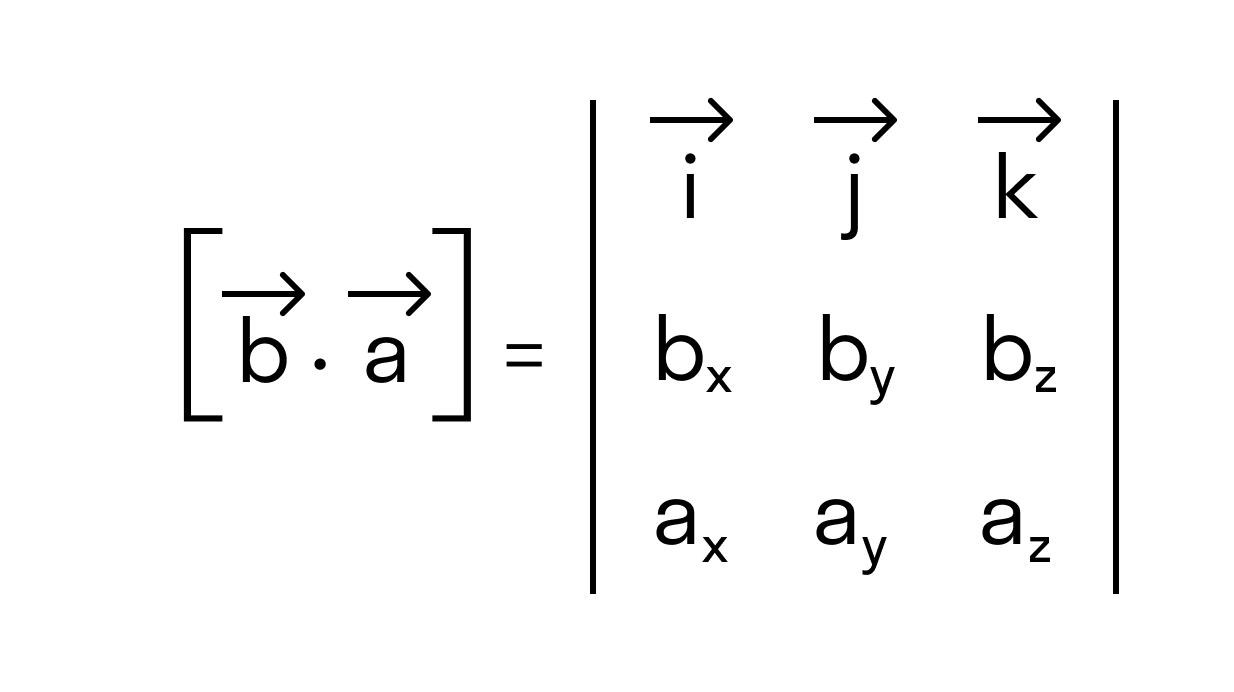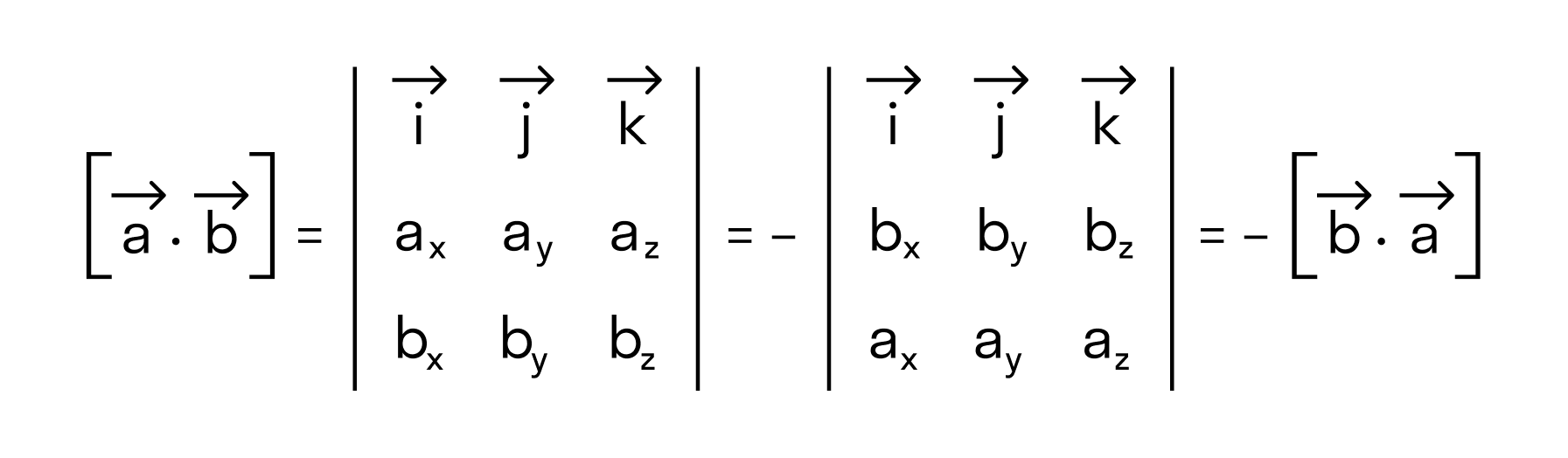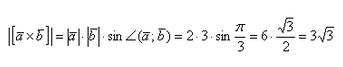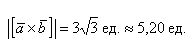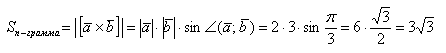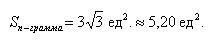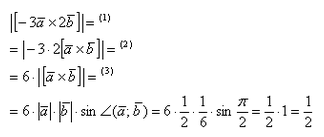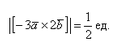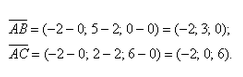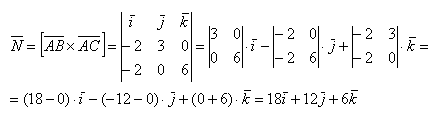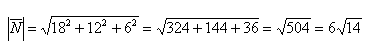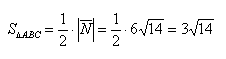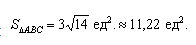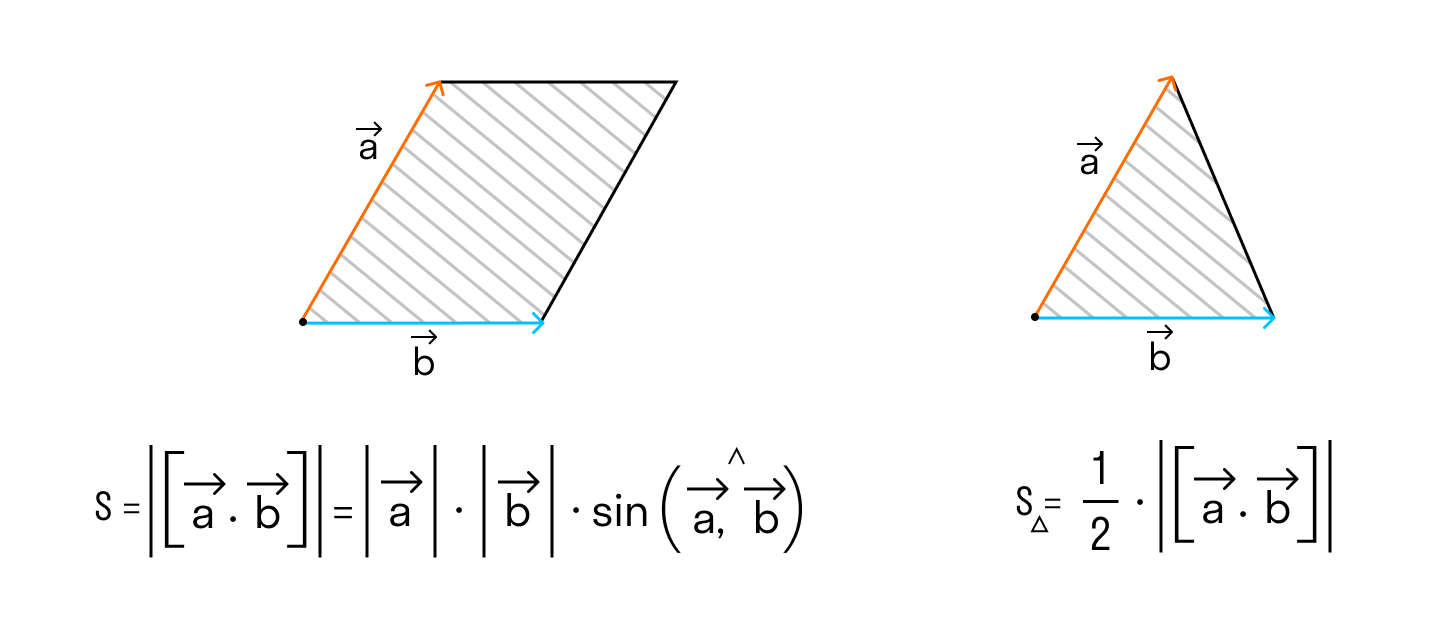что такое произведение сторон
Сюжет — это что такое? Примеры увлекательных сюжетов в литературе
Сюжет: определение и особенности
Сюжет в литературе является основой формой произведения. Он показывает ряд событий, которые происходят в произведении, выстроенных определенным образом.
Сюжет состоит из определенных составляющих: экспозиция, завязка, развитие действия, кульминация. Также может присутствовать пролог и эпилог.
Рис. 1. Составляющие сюжета в таблице.
Пролог – это вступление, эпилог – заключительная часть, не всегда связанная с сюжетом произведения
В экспозиции обычно происходит знакомство с главными героями, читатель начинает вникать в суть истории и понимать причину, по которой в дальнейшем произойдет конфликт. Экспозиция всегда предшествует началу сюжета, однако может следовать как после завязки, так и до нее.
Начало действия происходит завязка, в которой и обнаруживаются противоречия, которые волнуют главных героев.
Например, в трагедии Шекспира «Гамлет» завязкой является встреча героя с призраком.
Кульминация в произведении – это самый напряженный момент, который становится переломным и влияет на дальнейшие события и на мировоззрение героев.
Однако сюжет в литературе может встречаться не во всех литературных произведениях. Например, в лирических текстах сюжет зачастую и вовсе отсутствует, так стихотворные жанры передают чувства героев, а не повествуют о их действиях и поступках.
Очень близким понятием к сюжету является фабула. Однако считается, что они все-таки различаются. Сюжет – это ход событий, выстроенных в определенном порядке, а фабула подразумевает под собой освещение основного конфликта, который по ходу этих событий развивается. Однако существует мнение, что фабула не является самостоятельным элементом и сама по себе значения не имеют, поэтому при анализе произведения всегда говорят про сюжет,но очень редко про фабулу.



Что же такое сюжет
Аристотель, создатель реалистической эстетики античности, в своей “Поэтике” уделяет большое место проблеме сюжета, определяя его как “подражание действию”, “сочетание фактов”. При этом Аристотель настаивает на утверждении доминирующей роли сюжета в драме, в частности в трагедии, которая “есть подражание не людям, но действию и жизни”, цель которой — “какое-нибудь действие, а не качество” и для которой сюжет “есть основа и как бы душа”.
В повествовательных произведениях сюжет составляет их драматическую сторону (что допускает возможность их инсценировки), которая здесь совмещается с более или менее развитым описанием, а также авторскими высказываниями эмоционально-лирического, философского или публицистического характера.
В русскоязычной литературе бытуют два понятия — сюжет и фабула. Означают они примерно одно и то же, но есть и различия.
Если говорить кратко и просто, то:
К примеру, в романе Достоевского «Преступление и наказание» фабула такова:
Бедный студент совершил убийство старухи-ростовщицы. После долго мучился и раскаялся. Признался, пошел на каторгу и обрел покой и счастье.
Бедный студент, размышляющий над новейшими философскими концепциями своего времени, воспринимает старуху-ростовщицу как обезличенное зло, которое стоит на его пути, пути просвещенного и потенциально великого человека, и все в его жизни зависит от того, хватит ему решимости и смелости признаться, что он выше ее и имеет право ее уничтожить, чтобы достичь всего того, что он может; сможет ли он быть настоящим человеком, а не дрожащей тварью.
Чтобы доказать себе, что он человек, а не тварь, студент старуху убивает — топором, неумело и с ужасом; сцена убийства потрясает его настолько, что он впадает в шоковое состояние и постепенно скатывается в психическое расстройство… и так далее.
Думаю, этого достаточно, чтобы вы поняли разницу между фабулой и сюжетом.
Виды сюжета
Принято выделять концентрический сюжет и хроникальный. Данная классификация основана на отличии связей между событиями. Если в хроникальном сюжете главное внимание уделяется времени и его течению, то в концентрическом сюжете упор делается на психические факторы. Именно поэтому с первым сюжетом обычно имеют дело авторы саг и хроник, а второму отдают предпочтение писатели-фантасты, романисты и другие, для которых хронология событий не имеет принципиального значения.
В концентрическом сюжете всё просто и понятно: автор исследует только какой-то один конфликт, а элементы композиции легко выделить и назвать, так как они идут один за другим. Здесь все эпизоды будут иметь причинно-следственную связь, и весь текст будет пронизан чёткой логикой: никакого хаоса, никаких композиционных нарушений.
Даже если в произведении будет задействовано несколько сюжетных линий, все события будут связаны между собой по принципу звеньев одной цепи. С хронологическим сюжетом всё обстоит несколько иначе: тут причинно-следственные связи могут разрываться или вовсе отсутствовать. К тому же, некоторых элементов композиции может просто не быть.
Стивен Кинг, Томас Харрис и Джоан Роулинг
На десерт мы оставляем книги, где сюжет и герои (как составляющая последнего) играют решающую роль в популярности произведений авторов.
Стивен Кинг написал много книг. Какие-то из них удачные, какие-то не очень. Но некоторые стали культовыми у читателя. Например, «Мертвая зона», «Кладбище домашних животных», «Зеленая миля» и др. В них умело сочетается, с одной стороны, сюжетность, а с другой стороны, некоторая психологическая глубина, которая совершенно необходима любой хорошей художественной прозе.
Томас Харрис создал обаятельного маньяка. У Ганнибала Лектера не так уж много в этом смысле соперников. С одной стороны, трилогия о Ганнибале увлекательно читается, но она очень хорошо запоминается, потому что главный герой, несмотря на то что он психопат, вызывает восхищение.
У подготовленного читателя уйдет не так много времени на освоение всех книг Харриса, ибо их всего 5:
Нельзя напоследок не сказать и о Джоан Роулинг – создательнице культового среди подростов персонажа – Гарри Поттера. В целом, как и другие авторы в этом подразделе, Роулинг не претендует на высокое звание классика литературы (разве что в своем жанре), но она пишет хорошую прозу, которая вызывает сопереживание читателя. С книгами о Потере стоит ознакомиться всем, и даже взрослым. Помните, что дети не будут читать плохую литературу (так считает Д.Л. Быков).
Литература
Определение понятия в различных источниках
Само слово заимствовано из французского языка (subjet), что дословно переводится как «предмет». Во множестве источников (в различных словарях в том числе) значение слова варьируется. Что такое сюжет? Определение в среднем представляет собой систему событий и взаимоотношений между героями и развитие их во времени и пространстве. Вкратце сюжет обозначается совокупностью событий и действий, раскрывающих основное содержание произведения. Однако, например, «Словарь эстетики» 1989 г. называет сюжетом динамический аспект произведений искусства, развертывание действия, развитие взаимоотношений героев, их характеров, поступков. Повествовательным ядром художественного произведения считается сюжет в «Словаре литературных терминов», системой расположенности и взаимонаправленности лиц в данном произведении, а также положений и событий, развивающихся в нем. В «Большом энциклопедическом словаре» и «Современной энциклопедии» (2000) сюжет считается способом развертывания фабулы, а также последовательностью изображаемых событий.
Типология сюжетов
Предпринимались неоднократные попытки классифицировать сюжеты литературных произведений, разделять их по различным признакам, выделять наиболее типичные. Анализ позволил, в частности, выделить большую группу так называемых «бродячих сюжетов» — сюжетов, которые многократно повторяются в различном оформлении у разных народов и в разных регионах, большей частью — в народном творчестве (сказки, мифы, легенды).
По мнению А. Е. Нямцу, из всего многообразия традиционных сюжетов можно выделить четыре основные генетические группы: мифологические, фольклорные, исторические и литературные[2].
Как отмечает проф. Е. М. Мелетинский, «большинство традиционных сюжетов восходит на Западе к библейским и античным мифам»[3].
Известно несколько попыток свести всё многообразие сюжетов к небольшому, но при этом исчерпывающему набору сюжетных схем. В известной новелле «Четыре цикла» Борхес утверждает, что все сюжеты сводятся всего к четырём вариантам:
Французский исследователь Жорж Польти опубликовал в 1895 году книгу «Тридцать шесть драматических ситуаций», в которой свёл весь опыт мировой драматургии к разрабатыванию 36 стандартных сюжетных коллизий.
Сколько существует сюжетов
Исследователи фольклора (это что?), который, как известно, стоит у истоков авторской литературы, определили, что в основе сюжета лежит миф.
Распавшись на отдельные осколки, миф превратился в сказку (это что?). Собиратели «сказочных осколков» попытались собрать воедино сюжеты сказок по всему миру, что привело их к удивительному открытию: в культуре всех народов есть общие метасюжеты.
Самой известной стала классификация С.Томпсона «Указатель сказочных сюжетов». Томпсон взял за основу более подробную классификацию А.Аарне.
В настоящий момент количество указателей очень велико. Одни учёные насчитывают около 500 сюжетов, другие говорят, что их 200, третьи называют минимальное количество – 12.
Самым лаконичным оказался латиноамериканский писатель, исследователь литературы Х.Л.Борхес, который свёл всё богатство мировой культуры к четырём сюжетам. Всё остальное в его трактовке – лишь их вариация.
Например, сюжет о плуте, путешествующем по свету, представлен в классическом произведении древности – поэме Гомера «Одиссей».
В европейском средневековом искусстве он продолжился «Романом о Лисе». «Гаргантюа и Пантагрюэль» Ф.Рабле, «Мёртвые души» Н.В.Гоголя, «Уллис» Дж.Джойса, «Двенадцать стульев» И.Ильфа и Е.Петрова – вариации того же древнего мифа.
Определение слова «Сюжет» по БСЭ:
Фабула
Фабула — повествование о событиях в их хронологическом порядке; связь всех мотивов в произведении; все происшествия, которые отразись в драматическом, эпическом или лиро-эпическом произведении.
Элементы фабулы:
«Преступление и наказание» без ницшеанства и духовных мытарств главного героя
Не многие школьники осиливают это замечательное произведение. А ведь если бы его написал не Достоевский, то оно бы читалось, возможно, на одном дыхании. А потом сделали бы по ней экранизацию, и получилось что-то вроде «Лейтенанта Коломбо» в 19 веке.
Ведь если посмотреть непредвзято, без снобизма, то сюжет – это то в «Преступлении и наказании», что делает Порфирий Петрович. Посмотрим только на цепь событий. Читателю сразу известен преступник, злодеяние, короче говоря, казалось бы, нет интриги, но нет, Федор Михайлович не зря мастер детективной прозы. Основная интрига сюжета в том, признается Раскольников или нет. А Порфирий Петрович искусно подводит преступника, отягощенного совестью, к чистосердечному признанию, совсем как лейтенант Коломбо.
Сюжет
Сюжет — это цепь событий в определенной последовательности; развитие действия в драматическом, эпическом или лиро-эпическом произведении. Данный термин впервые применили французские классицисты П. Корнель и Н. Буало в XVII веке, заявив, что сюжет — «происшествия в жизни легендарных героев древности».
Сюжет — это обобщающая мысль писателя; это темы, проблемы, поставленные автором в произведении. Именно поэтому сюжет не может быть пересказан!
М.А. Булгаков как сатирик. «Мастер и Маргарита» без Воланда
Стивен Кинг утверждал в автобиографическом сочинении: «История начинается с вопроса, а что было бы если…». Кстати, по мнению короля ужасов, это некоторый творческий метод создания сюжета для приключенческой литературы в принципе. Здесь мы толкуем прилагательное «приключенческая» в широком ключе как «событийная».
«Мастер и Маргарита» – роман многослойный и пронизанный различными переплетениями между двумя почти полноправными его частями, «советскими» и «ершалаимскими» главами. Обычному же читателю он интересен прежде всего неповторимым стилем М.А. Булгакова и авторской фантазией о том, что сатана посетил Советский Союз в такое страшное время (30-е годы).
Конечно, возможно, «евангелие» от М.А. Булгакова важно, но если бы не Воланд и его похождения, роман не имел бы такого оглушительного успеха у современного читателя. Потому что все проблемы России, которые были явлены в эпохальном романе, остались на месте. Однако мы заговорись, а меж тем пора переходить к другой сюжетной прозе.
Что такое произведение в математике?
Произведение – это умножение.
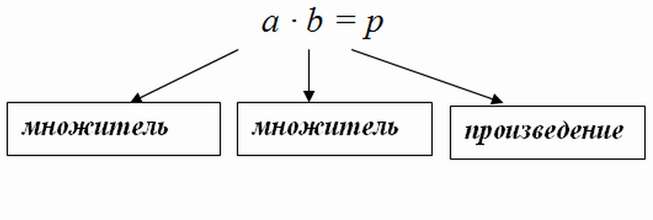
Так выражение вида a • b, а также значение этого выражения называют произведением чисел a и b. Числа a и b – это множители. Произведения как 3 • 4, так и 4 • 3 равны одному и тому же числу 12.
3 и 4 – множители, а 12 – произведение.
При перестановке множителей значение произведения не изменяется. Такое свойство выражения называют переместительным. Если его записать буквами, то оно будет выглядеть так:
Сочетательное свойство умножения выглядит так: a • (b • с) = (а • b) • c.
В произведении трёх и более множителей при их перестановке или изменении порядка выполнения умножения результат не изменяется.
Пример:
(4 • 2) • 3 = 8 • 3 = 24 или 4 • (2 • 3) = 4 • 6 = 24
Произведение любого натурального числа и единицы равно самому этому числу.
Произведение любого натурального числа и нуля, равно нулю.
Произведения с буквенными множителями записываются следующим образом:
вместо 6 • x пишут 6x, вместо a • b пишут ab
Также опускают знак умножения и перед скобками,
вместо 4 • (a + b) пишут 4(а + b),
вместо (x + 2) • (y + 3) пишут (x + 2)(y + 3),
вместо a • (b • c) пишут abc.
Вместе со статьёй «Что такое произведение в математике?» читают:
Векторное произведение векторов
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
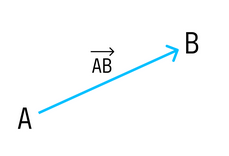
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
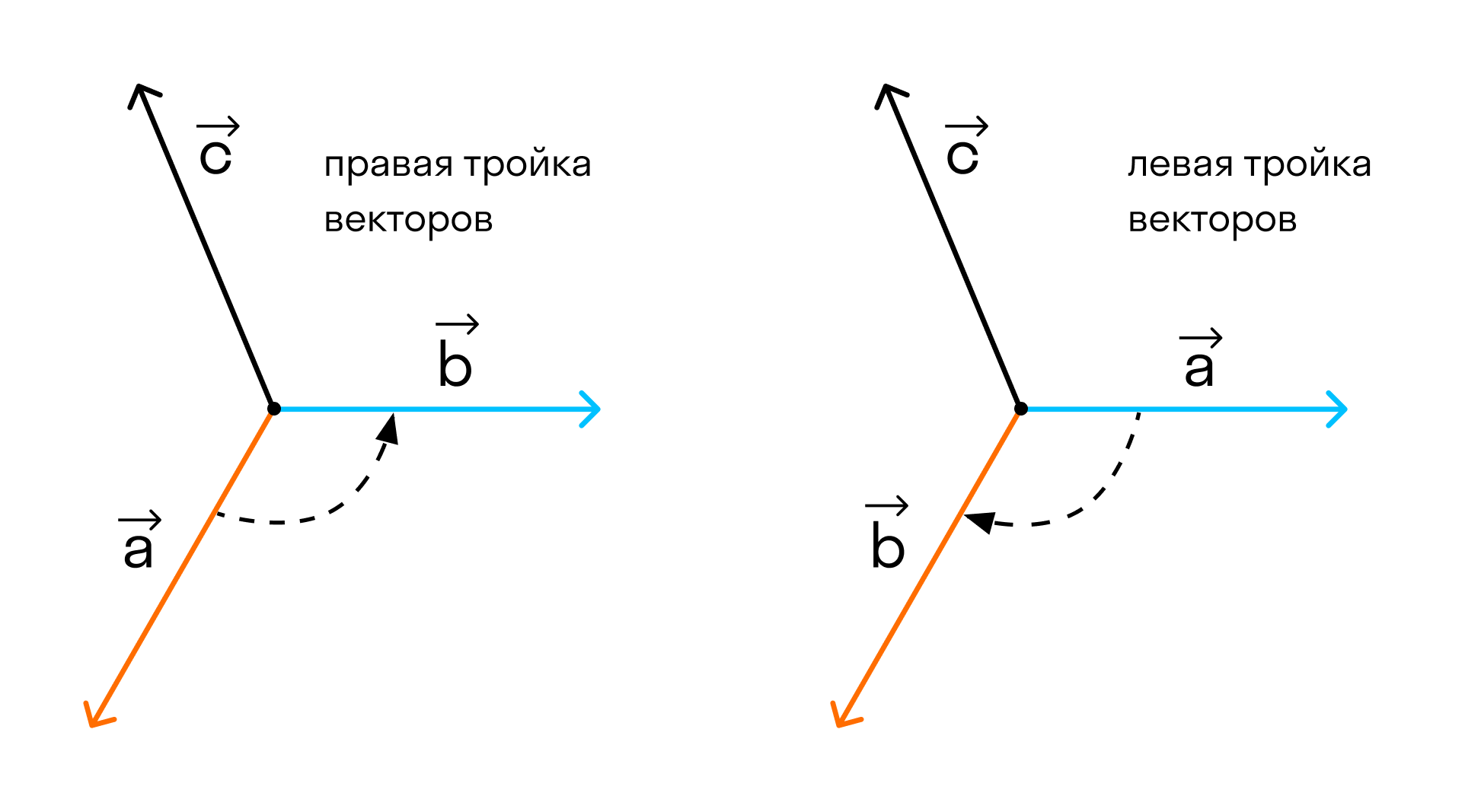
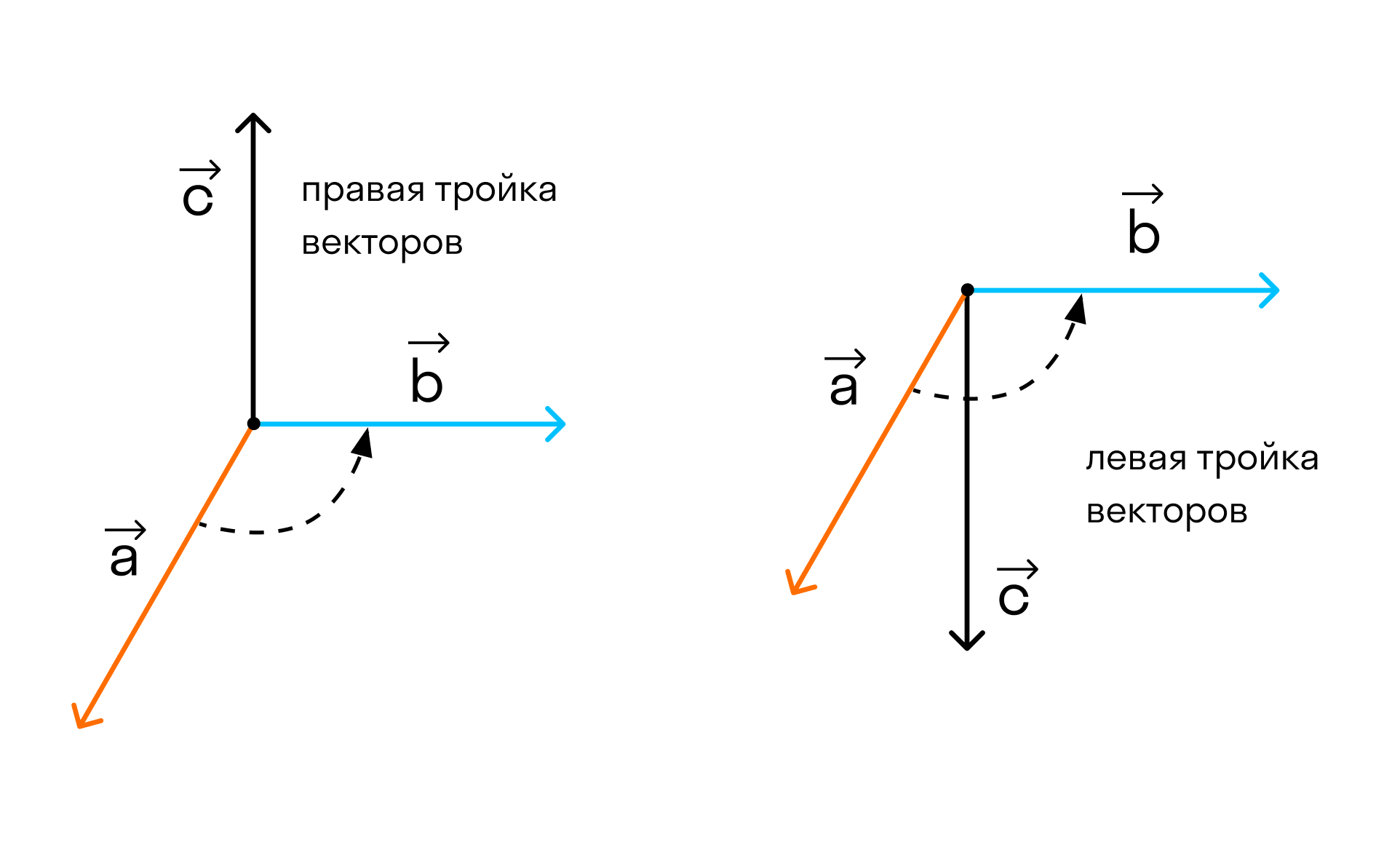
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
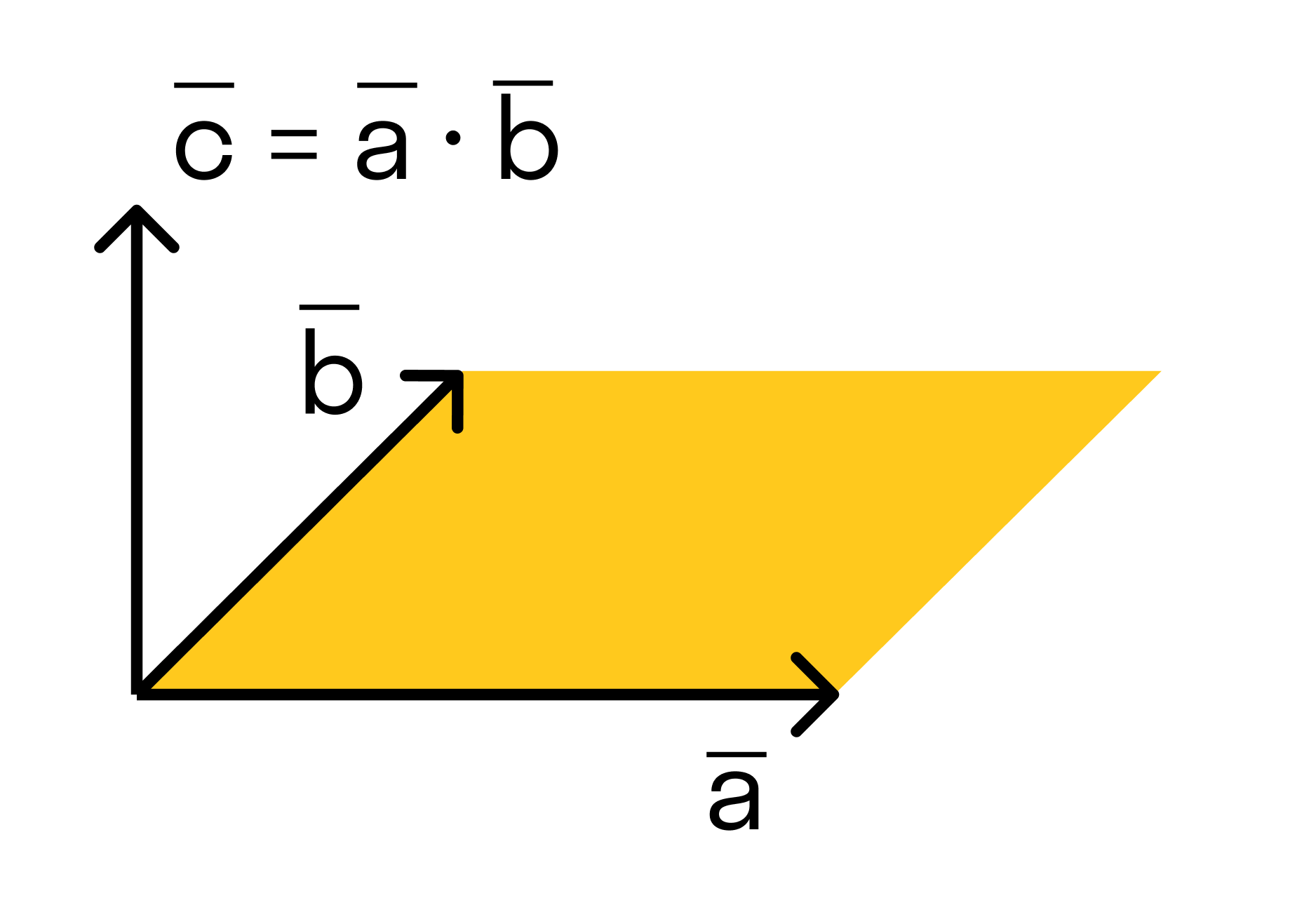
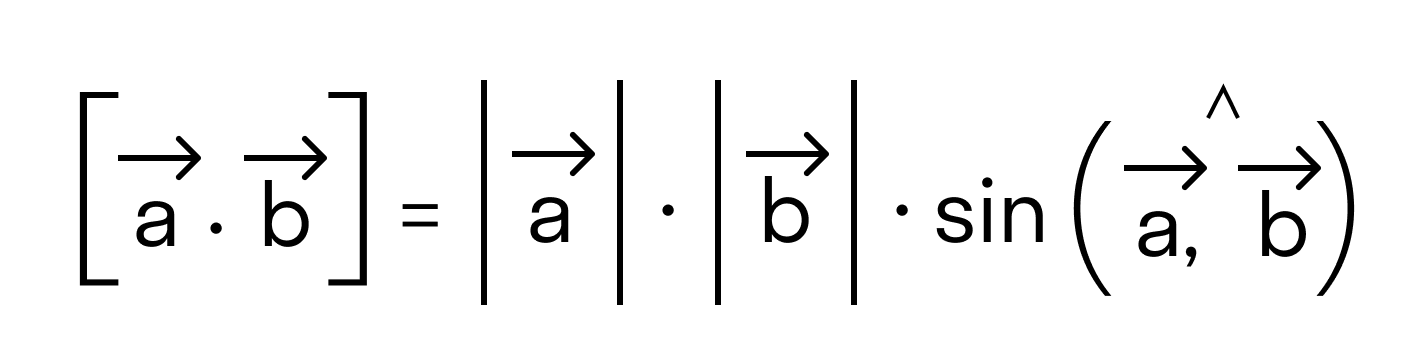
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a =
Векторное произведение векторов →a и →b обозначается как [→a • →b].
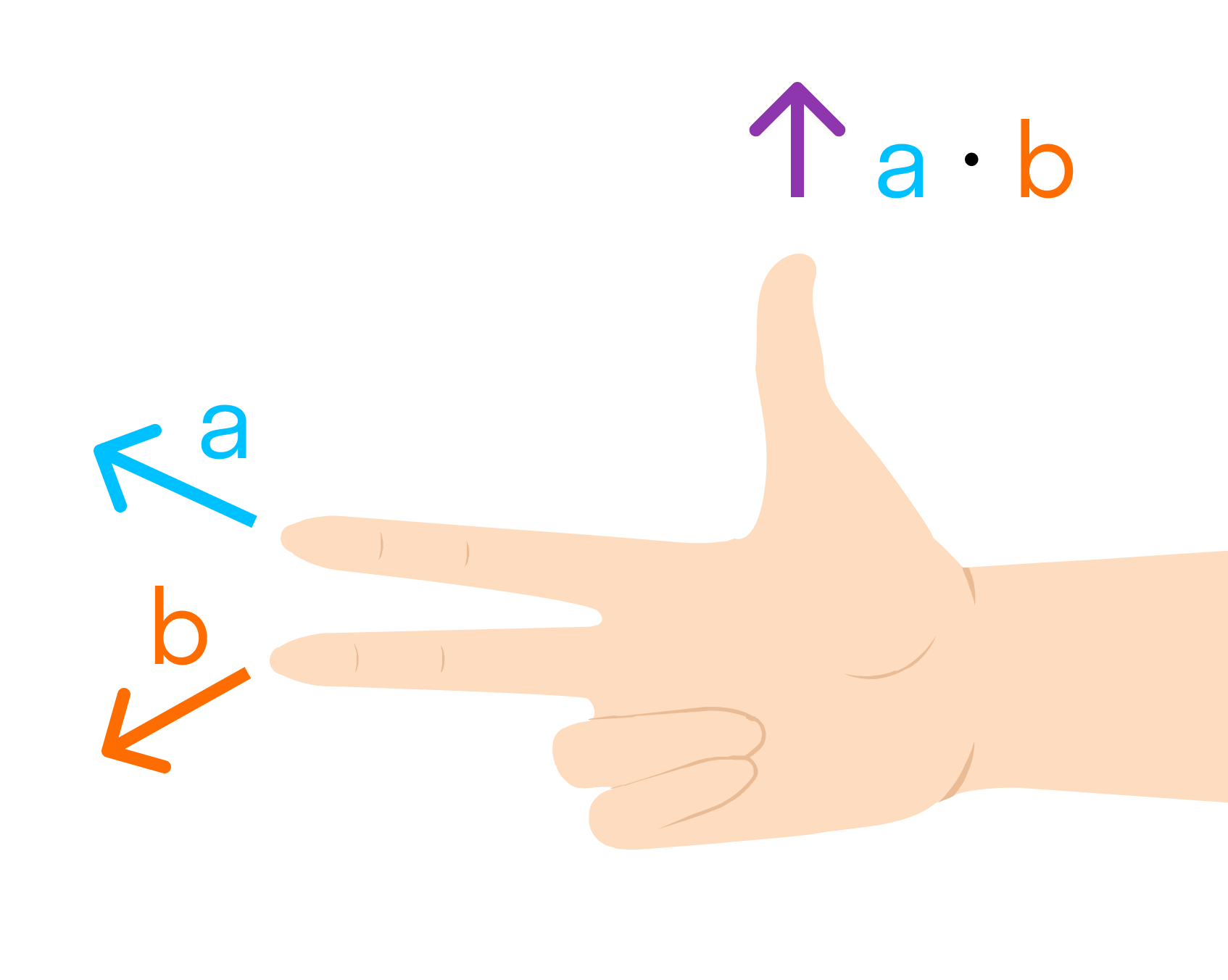
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
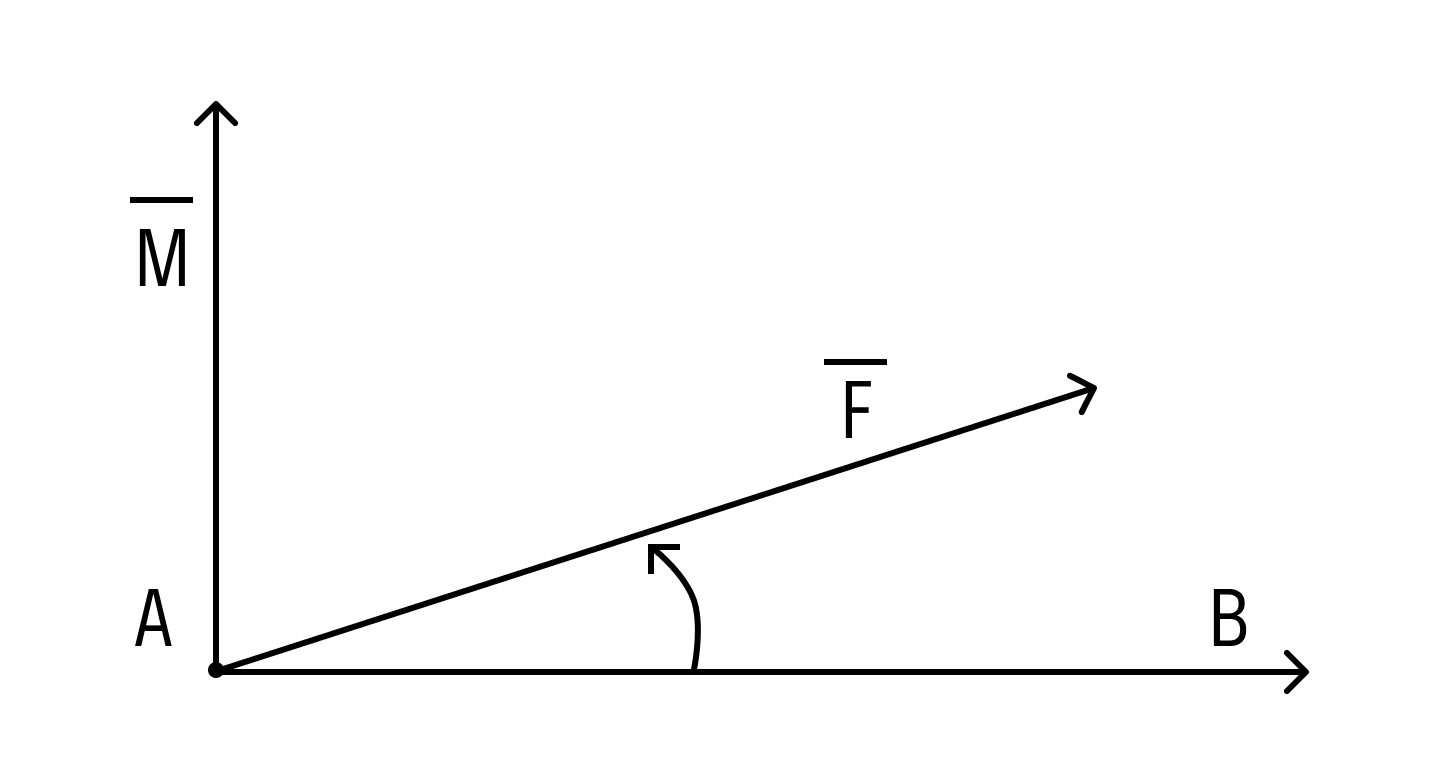
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.