что такое произведение чисел частное чисел и разность чисел
Числовые и буквенные выражения
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8
Как найти разность чисел в математике
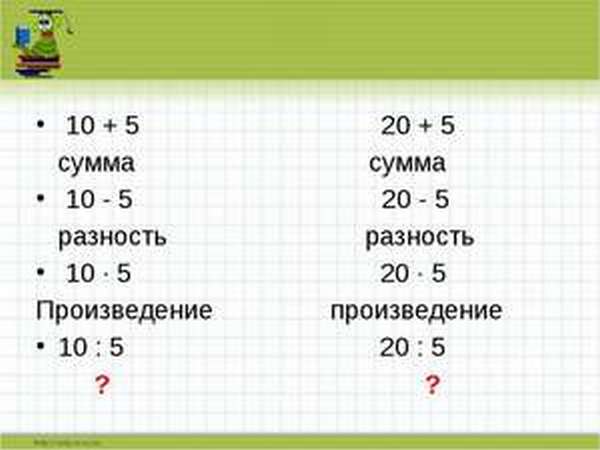
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
Это интересно: что такое модуль числа?
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Простые примеры
20 — уменьшаемое значение,
Ответ: 5 — разница величин.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
17 — уменьшаемая величина.
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
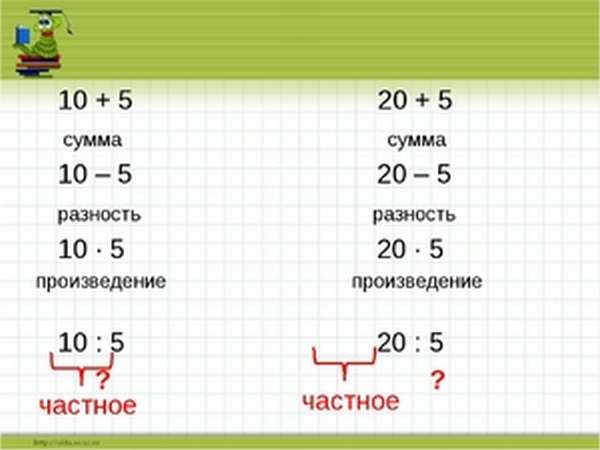
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),
Ответ: 40 — разница трёх значений.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
7 — уменьшаемая величина,
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
Частное в математике — определение, свойства и формула
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Свойства умножения и деления
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется.
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
В обратную сторону распределительное свойство умножения относительно сложения звучит так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
В обратную сторону распределительное свойство умножения относительно вычитания звучит так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число.
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?
Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.
Пример 2
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 3
Упростить выражение: 27a – 16a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.








