что такое продолжение стороны
Значение слова «продолжение»
1. Действие по знач. глаг. продолжить—продолжать и продолжиться—продолжаться. Продолжение начатой работы. Продолжение учебного курса. □ Я стал смотреть на продолжение ужасной комедии. Пушкин, Капитанская дочка.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ПРОДОЛЖЕ’НИЕ, я, ср. Действие по глаг. продолжить-продолжать и продолжиться-продолжаться. П. начатой работы. П. следует (примечание под неоконченным произведением, указывающее, что оно будет продолжено в следующем номере газеты, журнала). || То, что продолжено, часть чего-н. продолженного. Деревянный забор — п. каменной стены. ◊
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
продолже́ние
2. то, что продолжено, продолжается; часть чего-либо продолженного ◆ В любой выпуклый дельтоид можно вписать окружность, кроме этого, если дельтоид не является ромбом, то существует ещё одна окружность, касающаяся продолжений всех четырёх сторон. Для невыпуклого дельтоида можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон и окружность, касающуюся двух меньших сторон и продолжений двух бо́льших сторон.
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: повсеместность — это что-то нейтральное, положительное или отрицательное?
продолжение стороны
Смотреть что такое «продолжение стороны» в других словарях:
Операция «Продолжение надежды» — «Продолжение надежды» ( en. Continue Hope; UNOSOM II) миротворческая операция ООН в Сомали, проводившаяся в 1993 1995 годах, являвшаяся продолжением операции «Возрождение надежды». Одна из наиболее неудачных миротворческих … Википедия
Война-продолжение — Советско финская война (1941–1944) Вторая мировая война Финские САУ StuG III в Карелии Дата 25 июня 1941 – 19 сентября 1944 … Википедия
Война-Продолжение — Советско финская война (1941–1944) Вторая мировая война Финские САУ StuG III в Карелии Дата 25 июня 1941 – 19 сентября 1944 … Википедия
Операция «Продолжение надежды» — Немецкий миротворец в Беледуэйн, октябрь 1993 года «Продолжение надежды» (англ. Continue Hope; UNOSOM II) миротворческая операция ООН в Сомали, проводившаяся в 1993 1995 годах, являвшаяся продолжением операции «Возрождение надежды». Одна из… … Википедия
Александр II (часть 2, I-VII) — ЧАСТЬ ВТОРАЯ. Император Александр II (1855—1881). I. Война (1855). Высочайший манифест возвестил России о кончине Императора Николая и о воцарении его преемника. В этом первом акте своего царствования молодой Государь принимал пред лицом… … Большая биографическая энциклопедия
Александр II (часть 2, XIII-XIX) — XIII. Дела внутренние (1866—1871). 4 го апреля 1866 года, в четвертом часу дня, Император Александр, после обычной прогулки в Летнем саду, садился в коляску, когда неизвестный человек выстрелил в него из пистолета. В эту минуту, стоявший в… … Большая биографическая энциклопедия
Ломоносов, Михаил Васильевич — — ученый и писатель, действительный член Российской Академии Наук, профессор химии С. Петербургского университета; родился в дер. Денисовке, Архангельской губ., 8 ноября 1711 г., скончался в С. Петербурге 4 апреля 1765 года. В настоящее… … Большая биографическая энциклопедия
Семейство полорогие — (Bovidae)** * * Семейство полорогих, или бычьих самая обширная и разнообразная группа парнокопытных, включает 45 50 современных родов и около 130 видов. Полорогие животные составляют естественную, ясно очерченную группу. Как ни… … Жизнь животных
Пушкин, Александр Сергеевич — — родился 26 мая 1799 г. в Москве, на Немецкой улице в доме Скворцова; умер 29 января 1837 г. в Петербурге. Со стороны отца Пушкин принадлежал к старинному дворянскому роду, происходившему, по сказанию родословных, от выходца «из… … Большая биографическая энциклопедия
Теорема Менелая
Определение Теоремы Менелая
Теорема Менелая показывает соотношение сторон треугольника, которое получается, когда прямая пересекает две стороны треугольника и продолжение третьей.
С помощью этой теоремы можно получить соотношения сторон треугольника и доказать коллинеарность точек, которые находятся на данном треугольнике (на двух сторонах и продолжении третьей).
Коллинеарными точками называются три или более точки, которые лежат на одной прямой.
Теорема Менелая гласит:
BD/DC * CE/EA * AF/FB = 1
Шаг 1. Есть треугольник ABC. Прямая пересекает две стороны треугольника, таким образом, что она не проходит через вершину треугольника (на нашем рисунке это розовая линия). Таким образом получились две точки пересечения прямой с двумя сторонами треугольника (точки E и D). Третью сторону (AB) нужно продолжить до пересечения (получилась точка пересечения F).
Шаг 2. Берём точку треугольника и начинаем двигаться в другую точку треугольника, проходя через точку пересечения (потом делим один на другой): BD/DC
Обратите внимание, что в такой записи видно точку пересечения посередине («DD»), а B и C (сторона треугольника, по которой мы идём) по бокам. Т. е. мы идём из B к C через D. Можно написать точки стороны, по которой мы идём («BC»), оставив небольшое место между ними, и потом вставить между ними дважды точку пересечения со знаком дроби («D/D»).
В записи дробью точка, через которую мы идём повторяется наискосок.
На рисунке обозначить карандашом стрелочками по какой стороне мы уже прошлись и в какую сторону, и не запутаетесь.
Шаг 3. Идём дальше по треугольнику, делаем сторону CA — это будто прийти от C к A через E, что получается CE/EA.
Эти две стороны умножаются и в тетради, записывается всё вместе:
Шаг 4. Теперь делаем сторону AB через точку F — из A мы сначала пойдём в F, а потом уже вернёмся к B, получится так: AF/FB.
Шаг 5. Перемножаем всё вместе:
Теорема Менелая гласит:
BD/DC * CE/EA * AF/FB = 1
Доказательство теоремы Менелая
Есть много способов доказать эту теорему, этот называется «Доказательство с подобными треугольниками»:
Проводим линию, которая параллельна QN через точку A, чтобы пересечь сторону BC в точке M.
Теорема Менелая пример (задача с решением)
Есть треугольник АВС. На стороне ВС стоит точка L, такая, что LC = 3BL. За точку А идёт продолжение стороны АС, где взята точка М, таким образом, что МА = АС. Прямая ML пересекает АВ в точке F.
Найдите соотношение BF/FA:
1. Мы знаем, что МА = АС, LC = 3BL.
2. Прямая ML пересекает две стороны треугольника АВС и является продолжением третьей, значит по теореме Менелая:
Что такое теорема Чевы?
Пусть на сторонах треугольника ABC отмечены точки A’, B’ и C’. Отрезки AA’, BB’ и CC’ пересекаются в одной точке тогда и только тогда, когда справедливо равенство:
Заметьте, что логика та же самая: идём из А в С через В’ и т. д.
Чевиана — это отрезок, который соединяет вершину треугольника с точкой на противоположной стороне.
Что такое продолжение стороны
Дан параллелограмм ABCD с острым углом А. На продолжении стороны AD за точку D взята точка N, такая, что CN = СD, а на продолжении стороны CD за точку D взята такая точка M, что AD = AM.
а) Докажите, что BM = BN.
б) Найдите MN, если AC = 7,
а) Рассмотрим треугольники BCN и BAM. По условию AM = AD = BC, AB = CD = CN. В равнобоких трапециях NABC и ABCM равны углы A и C, а значит, равны и углы MAB и BCN. Таким образом, треугольники BNC и BAM равны по двум сторонам и углу между ними, значит, равны и их соответственные стороны BN и BM. Что и требовалось доказать.
б) Заметим, что ABCM и NABC — равнобокие трапеции, тогда равны их диагонали, поэтому AC = BM = BN = 7. Имеем:
Теперь применим теорему косинусов для треугольника MBN:
откуда
Ответ:
| Критерии оценивания выполнения задания | Баллы | |||||
|---|---|---|---|---|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 | |||||
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 | |||||
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Угол. Биссектриса. Виды углов.теория по математике 📈 планиметрияУгол – геометрическая фигура, состоящая из точки и двух лучей, которые исходят из этой точки. Лучи – стороны угла, а точка – вершина. Обозначение углов: можно обозначать тремя заглавными латинскими буквами (в середине записи – буква, которая обозначает вершину угла); можно обозначать одной заглавной латинской буквой; также используется обозначение двумя прописными латинскими буквами. Рассмотрим обозначение на рисунках, где на рисунке 1 показан угол АОС, на рисунке 2 – угол М, на рисунке 3 – угол (hc).
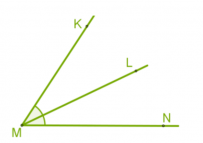
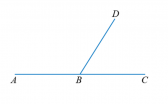
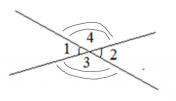
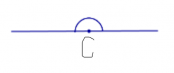
Измерение углов. Виды угловОбычно за единицу измерения углов принимают градус – угол, равный одной стовосьмидесятой части развернутого угла. Эта единица измерения введена до нашей эры много веков назад и используется в наше время. Число, которое указывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла. Определенные части градуса носят такие названия, как минута и секунда, где минута – это 1/60 часть угла, а секунда – это 1/60 часть минуты. Запись и чтение осуществляется следующим образом: 78 0 (78 градусов); 24 0 32 / 45 // — это 24 градуса 32 минуты 45 секунд. Определение Угол называется развернутым, если обе его стороны лежат на одной прямой. Также можно сказать, что одна сторона развернутого угла является продолжением другой стороны этого угла. На рисунке показан развернутый угол С. Его величина равна 180 градусам (180 0 ). Угол, градусная мера которого равна 90 градусов, называется – прямой. Биссектриса углаБиссектрисой угла называется луч, исходящий из вершины и делящий его на два равных угла. На рисунке показан луч ML, который делит угол KMN пополам, то есть угол KML равен углу LMN. Смежные углыДва угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. На рисунке показаны углы ABD и DBC, которые являются смежными, у них сторона BD общая, а стороны АВ и ВС являются продолжениями одна другой. По рисунку мы видим, что эти два смежных угла образуют развернутый угол. Таким образом, сумма смежных углов равна 180 градусов. Это свойство смежных углов. Смежные углыДва угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла. Другими словами, при пересечении двух прямых образуются две пары вертикальных углов. На рисунке показаны две пары вертикальных углов, это пара углов 1 и 2, а также вторая пара – это 3 и 4.
|










 Определение
Определение