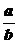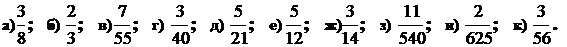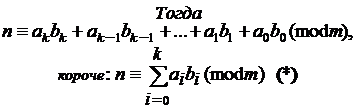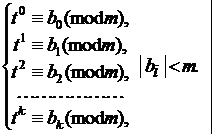Что такое приведенная система вычетов
Что такое приведенная система вычетов
– противоречие с тем, что x 1 и x 2 различны и взяты из полной системы вычетов.
Пример. Пусть m = 42. Тогда приведенная система вычетов суть:
1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.
Таковы определения и основные свойства полной и приведенной систем вычетов, однако в багаже математических знаний существует еще целый ряд очень интересных и полезных фактов, касающихся систем вычетов. Если умолчать про них в этом пункте, то это, боюсь, будет прямым нарушением Закона Российской Федерации об Информации, злонамеренное утаивание которой является, согласно этому закону, административно и, даже, уголовно наказуемым деянием. Кроме того, без знакомства с дальнейшими важными свойствами систем вычетов пункт 17 получится весьма куцым. Продолжим.
M s x s є M s x s С (mod m s ) Ю x s є x s С (mod m s )
Доказательство. Доказательство обоих утверждений леммы 4 легко получается применением предыдущей леммы 3 после того, как вы приведете каждую сумму
Доказательство. При а кратном m имеем: a=md и
ибо сумма всех корней степени m 1 из единицы равна нулю.
где m ( m ) – функция Мебиуса.
При a s =1 получается, что только корень e 0 =1 не является первообразным, поэтому сумма всех первообразных корней есть сумма всех корней минус единица:
Вот теперь, дорогие читатели, когда я представил на ваше рассмотрение довольно весьма значительное количество сведений про полные и приведенные системы вычетов, никто не сможет обвинить меня в злонамеренном нарушении Закона Российской Федерации об Информации посредством ее утаивания, поэтому я заканчиваю этот пункт с удовлетворением.
Чуть ниже выпишите приведенные системы вычетов по этим модулям. Нарисуйте отдельно на комплексной плоскости корни шестой и корни восьмой степени из единицы, на обоих рисунках обведите кружочком первообразные корни и найдите в каждом случае их сумму.
ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ
Смотреть что такое «ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ» в других словарях:
Приведенная система вычетов — Приведённая система вычетов по модулю m набор, составленный из всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(m) функция Эйлера. В качестве приведённой… … Википедия
Функция Эйлера — Не следует путать с функцией распределения простых чисел. Первая тысяча значений Функция Эйлера φ(n) мультипликативная … Википедия
СРАВНЕНИЕ — соотношение между целыми числами а и и вида a=b+mk, означающее, что их разность а b делится на заданное целое положительное число т, наз. модулем сравнения; при этом аназ. вычетом целого числа bпо модулю т. Для выражения сравнимости чисел аи bпо… … Математическая энциклопедия
Администрация США — (Administration of USA) Определение администрации США, высшие руководители США Определение администрации США, высшие руководители США, административные учреждения Содержание Содержание Определение Административное право Служба высших… … Энциклопедия инвестора
ЛОГИКА ВЫСКАЗЫВАНИЙ — раздел логики, в котором изучаются истинностные взаимосвязи между высказываниями. В рамках данного раздела высказывания (пропозиции, предложения) рассматриваются только с т.зр. их истинности или ложности, безотносительно к их внутренней субъектно … Философская энциклопедия
ПОЛНАЯ И ПРИВЕДЁННАЯ СИСТЕМЫ ВЫЧЕТОВ
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Классом чисел по данному модулю т называется множество всех тех и только тех целых чисел, которые при делении на т имеют один и тот же остаток r, то есть сравнимых по модулю т (т ÎN, т > 1).
Обозначение класса чисел, имеющих остаток r: 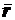
Каждое число из класса 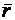
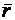
6. 2. Свойства множества классов вычетов 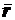
2) каждый класс 
ТИПОВЫЕ ЗАДАЧИ
1. Составить по модулю т = 9:
1) полную систему наименьших положительных вычетов;
2) полную систему наименьших неотрицательных вычетов;
3) произвольную полную систему вычетов;
4) полную систему наименьших по абсолютной величине вычетов.
2. Составить приведённую систему вычетов по модулю т = 12.
1) Составим полную систему наименьших положительных вычетов по модулю т = 12:
2) Вычеркнем из этой системы числа, не взаимно простые с числом 12:
3) Оставшиеся числа, взаимно простые с числом 12, образуют искомую приведённую систему вычетов по модулю т = 12 (всего j(т) = j(12) = 4 числа).
Ответ: <1, 5, 7, 11>– приведённая система вычетов по модулю т = 12.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
130. Составьте 1) полную систему наименьших положительных вычетов; 2) полную систему наименьших неотрицательных вычетов; 3) произвольную систему вычетов; 4) полную систему наименьших по абсолютной величине вычетов; 5) приведённую систему вычетов: а) по модулю m = 6; б) по модулю m = 8.
132 По какому модулю множество<20, – 4, 22, 18, – 1>является полной системой вычетов?
§ 7. ТЕОРЕМА ЭЙЛЕРА. МАЛАЯ ТЕОРЕМА ФЕРМА
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
7. 3. Теорема Эйлера.
Если аÎZ, тÎN, т >1 и (а; т) = 1, – то 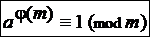
7. 4. Малая теорема Ферма (1601 – 1665).
Для любого простого числа р и любого числа аÎZ, не делящегося на р, имеет место сравнение 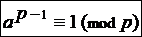
Пример. Пусть а = 3, р = 5, где 3 не 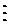
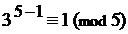
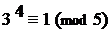
7. 5. Обобщёння теорема Ферма.
Для любого простого числа р и произвольного числа аÎZ имеет место сравнение 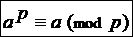
ТИПОВЫЕ ЗАДАЧИ
1. Докажите, что 38 73 º 3(mod 35).
1) Так как (38; 35) = 1, то по теореме Эйлера 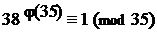
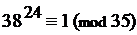
2) Из сравнения (1) по следствию 2 свойства 5 0 числовых сравнений имеем:
3) Из сравнения (2) по следствию 1 свойства 5 0 сравнений: 38 72 ×38 º 1×38 (mod 35) Þ Þ38 73 º38 º 38–35 = 3(mod 35) Þ 38 73 º 3 (mod 35), что и требовалось доказать.
2. Дано: а = 4, т = 15. Найти наименьший показатель степени k, удовлетворяющий сравнению 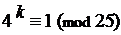
1) Так как (a; m) = (4; 25) = 1, то по теореме Эйлера 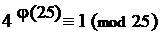
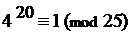
2) Является ли найденный показатель степени – число 20 – наименьшим натуральным числом, удовлетворяющим сравнению (*)? Если существует показатель степени, меньший 20, то он должен быть делителем числа 20. Значит, искомый наименьший показатель k надо искать среди множества чисел n = <1, 2, 4, 5, 10, 20>– делителей числа 20.
3) При п = 1: 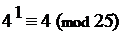
при п = 2: 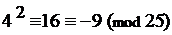
при п = 3: (рассматривать не надо);
при п = 4: 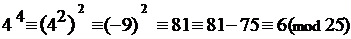
при п = 5: 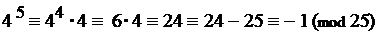
при п = 6, 7, 8, 9: (рассматривать не надо);
при п = 10: 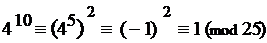
Итак, наименьшим показателем степени k, удовлетворяющим сравнению(*), является k= 10.
Ответ: 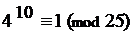
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
141. По теореме Эйлера 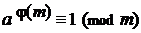
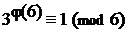
Так как j(6) = 2, то 3 2 º1(mod 6), или 9º1(mod 6), Тогда, по лемме, (9 – 1) 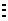
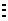
142. Докажите, что: а) 23 100 º1(mod 101); б) 81 40 º 1(mod100); в) 2 73 º 2 (mod 73).
143. Докажите, что а) 1 16 + 3 16 + 7 16 + 9 16 º 4 (mod 10);
б) 5 4п + 1 + 7 4п + 1 делится без остатка на 12..
144. Докажите теорему, обратную теореме Эйлера: если а j ( m ) º 1(mod m), то (а, m) =1.
145. Найдите наименьший показатель степени kÎN, удовлетворяющий данному сравнению: а) 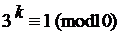
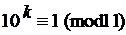
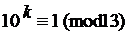
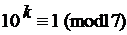
д) 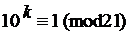
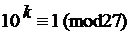
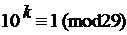
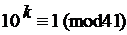
и) 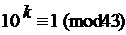
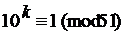
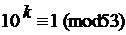
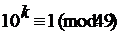
146. Найдите остаток от деления:
а) 7 100 на 11; б) 9 900 на 5; в) 5 176 на 7; г) 2 1999 на 5; д) 8 377 на 5;
е) 26 57 на 35; ж) 35 359 на 22; з) 5 718 на 103; и) 27 260 на 40; к) 25 1998 на 62.
147*. Докажите, что а 561 º а (mod 11).
148*. Если каноническое разложение натурального числа п не содержит множителей 2 и 5, то 12-я степень этого числа оканчивается цифрой 1. Докажите.
149*. Докажите, что 2 64 º 16 (mod 360).
Глава 3. АРИФМЕТИЧЕСКИЕ ПРИЛОЖЕНИЯ
ТЕОРИИ ЧИСЛОВЫХ СРАВНЕНИЙ
§ 8. СИСТЕМАТИЧЕСКИЕ ЧИСЛА
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. ЦЕЛЫЕ СИСТЕМАТИЧЕСКИЕ ЧИСЛА
Системой счисления называется всякий способ записи чисел. Знаки, с помощью которых записывают эти числа, называют цифрами.
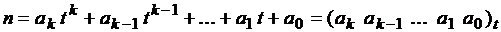
Например, запись числа в 7-ричной системе имеет вид: (5603)7 = 5 ×7 3 + 6×7 2 + 0×7 1 + 3. Здесь ai – это 5, 6, 0, 3 – цифры; все они удовлетворяют условию: 0 £ ai £ 6. При t =10 говорят: число n записано в десятичной системе счисления, причём индекс t=10не пишут.
Всякое целое неотрицательное число может быть представлено, причём единственным образом, в виде систематического числа по любому основанию t, где t Î N, t > 1.
1) приписывание к систематическому числу нулей слева не изменяет этого числа:
2) приписывание к систематическому числу s нулей справа равносильно умножению этого числа на t s : (3 4)5 = 3×5 1 + 4; (3 4 0 0)5 = 3×5 3 + 4×5 2 + 0×5 1 + 0 = 5 2 ×(3×5 1 + 4).
8. 5. Алгоритм перевода числа, записанного в t -ичной системе, в десятичную:
Пример: (287)12 = 2×12 2 + 8×12 1 +7×12 0 = 2×144 + 8×12 + 7 = 288 + 96 +7 = (391)10.
8. 6. Алгоритм перевода числа, записанного в десятичной системе, в t -ичную:
8. 7. Действия над систематическими числами
| осуществляются с помощью таблиц сложения и умножения размером t ´ t. Например, при t = 2 таблицы имеют вид: | + | 0 1 | ´ | 0 1 |
| 0 1 1 10 | 0 0 0 1 |
2. СИСТЕМАТИЧЕСКИЕ ДРОБИ
Конечной t-ичной систематической дробью в системе счисления с основанием t называется число вида
Всякая конечная систематическая дробь есть рациональное число, которое можно представить в виде 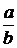
Пример. a = (3 1, 2 4)6 = 3×6 + 1 + 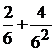
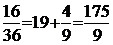
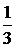
Бесконечной t-ичной положительной систематической дробью в системе счисления с основанием t называется число вида
Возможны три вида бесконечных систематических дробей:
II a = 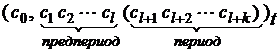
В этом случае число a называется бесконечной смешанной периодической дробью, 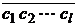
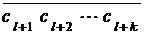
ТИПОВЫЕ ЗАДАЧИ
1) Преобразуем данное число (2 1 4 3) 5 в число (у)10, записанное в десятичной системе:
| (2 1 4 3) 5 = 2×5 3 +1×5 2 + 4×5 +3 = = 2×125 +1×25 + 4×5 +3 =250 +25 + 20+3 = (2 9 8) 10. 2) Преобразуем полученное число (у)10 в семеричную систему (х)7 (см. справа): Ответ: (2 1 4 3) 5 = (6 0 4) 7. | 298 28 18 14 4 = r1 |
| 42 42 | |
| 6 | |
| 0 = r2 | 0 0 6 = r3 |
2. Выполните действия:
4) (5 2 3 4) 7 – (2 3 5 1) 7; 5) (4 2 3 ) 5 × (3 2) 5; 6) (3 0 1 4 1) 5 : (4 2 3) 5.
Решение.
| 3) (3 6 4 2)6 + (4 3 5 1)6 (1 2 4 3 3)6 | Примечание: | 4+5 = 9 = 1×6+3, 3 пишем, 1 переходит в следующий разряд, 6+3+1=10 =1×6+4, 4 пишем, 1 переходит в следующий разряд, 3+4+1= 8 = 1×6+2, 2 пишем, 1 переходит в следующий разряд. |
| 4) (5 2 3 4)7 – (2 3 5 1)7 (2 5 5 3)7 | Примечание: | «занимаем» единицу высшего разряда, т. е. «1» = 1×7: (3 + 1×7 ) – 5 = 10 – 5 = 5, (1 + 1×7 ) – 3 = 8 – 3 = 5, |
| 5) (4 2 3)5 ´ ( 3 2)5 (1 4 0 1)5 + (2 3 2 4)5__ (3 0 1 4 1)5 | Примечание: | При умножении на 2 : 3 ×2 = 6 = 1×5 + 1, 1 пишем, 1 переходит в следующий разряд, 2 ×2 +1=5 = 1×5 +0, 0 пишем, 1 переходит в следующий разряд, 2 ×4 +1=9 = 1×5 +4, 4 пишем, 1 переходит в следующий разряд, При умножении на 3 : 3 ×3 = 9 = 1×5 + 4, 4 пишем, 1 переходит в следующий разряд, 3 ×2 +1=7 = 1×5 +2, 2 пишем, 1 переходит в следующий разряд, 3 ×4 +1=13=2×5 +3, 3 пишем, 2 переходит в следующий разряд. |
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
151. Числа, заданные в t-ичной системе, переведите в десятичную систему:
а) (2 3 5) 7 ; б) (2 4 3 1) 5 ; в) (1 0 0 1 0 1) 2 ; г) (1 3 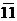
д) (2 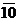
152. Числа. заданные в десятичной системе, переведите в t-ичную систему. Сделайте проверку.
153. Числа, заданные в t-ичной системе, переведите в q-ичную систему (путём перехода через десятичную систему).
а) (3 7) 8 = (х) 3; б) (1 1 0 1 1 0) 2 = (х) 5; в) ( 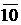
155. Выполните действия:
а) (3 0 2 1) 4 + (1 2 3 3) 4; б) (2 6 5 4) 8 + (7 5 4 3) 8; в) (1 0 1 1 0 1)2+(1 1 0 1 10)2;
г) (5 2 4 7) 9 + (1 3 7 6) 9; д) (4 7 6) 9 – (2 8 7) 9; е) (2 4 5 3) 7 – (1 6 4 5) 7;
ж) (8 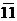
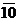
к) (1 0 0 1 0) 2 × (1 1 0 1) 2; л) (7 4 1) 8 × (2 6) 8; м) (5 3 7 2) 8 × (2 4 6) 8;
н) (3 3 2 1) 4 × (2 3 0) 4; о) (1 0 2 2 2 2) 3 : (1 2 2) 3; п) (2 1 0 3 2) 4 : (3 2 3) 4;
р) (2 6 1 7 4) 8 : (5 4 6) 8; с) (4 3 2 0 1) 5 : (2 1 4) 5; т)(1 1 0 1 0 0 1 0)2:(1 0 1 0 1)2
у) (1 1 0 1 1 0) 2 : (1 1 1) 2; ф) (1 1 1 0) 6 : (2 1 5) 6; х)(3 2 3 8 2 2 1 7 0)9:(7 6 4 2)9.
ц) (1 6 3 5) 8 + (7 6 4 ) 8; ч) (1 1 1 1) 3 – (2 1 2) 3; ш)(1 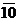
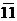
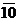
щ) (1 6 3 5) 8 × (7 6 4) 8; э) (9 5 7 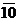
§ 9. ПЕРЕХОД ОТ РАЦИОНАЛЬНОГО ЧИСЛА ВИДА
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
9. 1. Установим условия, при которых число вида 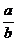
II Если знаменатель b = b1 (не содержит «2» и «5»), – то дробь 
III Если знаменатель b = b’ × b1 (содержит «2» и / или»5″, а также иные простые множители), – то дробь 
Длина периода равна наименьшему натуральному числу k, удовлетворяющему сравнению 10 k º 1(mod b1 ).
Длина предпериода равна наименьшему натуральному числу l, удовлетворяющему сравнению 10 l º 0(mod b‘ ).
| a | ↗ | к о н е ч н а я д е с я т и ч н а я д р о б ь |   | рацион. число  иррацион. число иррацион. число |
| ↘ | бесконечная десятичная дробь |  | 1) чисто периодическая дробь 2) смешанная периодич. дробь 3) непериодическая дробь |
рациональным числом является всякая конечная десятичная дробь или бесконечная периодическая десятичная дробь;
иррациональным числом является всякая бесконечная непериодическая десятичная дробь.
ТИПОВЫЕ ЗАДАЧИ
1. Данные обыкновенные дроби, записанные в десятичной системе, преобразовать в
десятичные, предварительно определив вид искомой дроби (конечная или бесконечная; периодическая или непериодическая; если – периодическая, то чисто периодическая или смешанная периодическая); в последних случаях – предварительно найти число k – длину периода и число l – длину предпериода. 1) 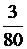
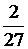
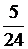
1) У дроби 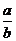
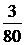
| Имеем:10 1 º10(mod80), 10 2 = 100 º20(mod80), 10 3 º200 º 40(mod80), 10 4 º400 º 0(mod80). | Следовательно, l наим = 4, то есть искомая десятичная дробь будет иметь 4 десятичных знака. Проверка: разделим «уголком» 3 на 80 и получим: 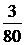 = 0, 0375. = 0, 0375. |
2) У дроби 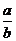
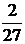
| Имеем: 10 1 º10(mod27), 10 2 º100–81º19(mod27), 10 3 º190 º190 – 7×27 º º 190 – 189 º 1(mod27). | Следовательно, k наим = 3, то есть в искомой десятичной дроби будет период длиной k = 3. Проверка: разделим «уголком» 2 на 27 и получим: 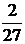 = 0, (074). = 0, (074). |
3) У дроби 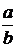
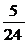
Проверка: разделим «уголком» 5 на 24 и получим: 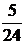
Ответ: 1) 0, 0375; 2) 0, (074); 3) 0, 208 (3).
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
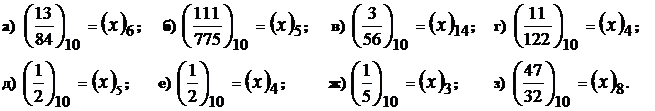
§ 10. ТЕОРЕМА ПАСКАЛЯ. ПРИЗНАКИ ДЕЛИМОСТИ
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
10. 1. Теорема Паскаля (1623 – 1662).
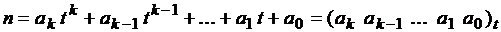
Пусть
Итак: из равенства (*) в теореме Паскаля следует, что число n и число 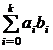
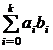
Для того, чтобы число n делилось без остатка на число т, необходимо и достаточно, чтобы сумма 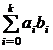
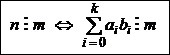
ТИПОВЫЕ ЗАДАЧИ
1. Установите в десятичной системе счисления признаки делимости на 3, на 9 и на 11.
1) Признаки делимости на 3 и на 9.
10 2 º1(mod3), т.е. b2 =1, 10 2 º1(mod9), т.е. b