Что такое приведенная функция
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида 
к функциям аргумента 
. С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до 
радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
Вычислить 
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+». Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
Формулы приведения: доказательство, примеры, мнемоническое правило
Данная статья посвящена подробному изучению тригонометрических формул приведения. Дан полный список формул приведения, показаны примеры их использования, приведено доказательство верности формул. Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
Формулы приведения. Список
Фомулы приведения позволяют приводить основные тригонометрические функции углов произвольной величины к функциям углов, лежащих в интервале от 0 до 90 градусов (от 0 до π 2 радиан). Оперировать углами от 0 до 90 градусов гораздо удобнее, чем работать со сколь угодно большими значениями, поэтому формулы приведения широко применяются при решении задач тригонометрии.
Прежде, чем мы запишем сами формулы, уточним несколько важных для понимания моментов.
Теперь перейдем непосредственно к формулам приведения.
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов. запишем все формулы в виде таблицы.
В данном случае формулы записаны с радианами. Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Примеры использования формул приведения
Покажем, как пользоваться формулами приведения и как указанные формулы применяются при решении практических примеров.
В зависимости от представления угла используется соответствующая формула приведения.
Возьмем тот же угол α = 16 π 3 и вычислим его тангенс
Пример 1. Использование формул приведения
Представим угол α = 16 π 3 в виде α = π + π 3 + 2 π · 2
Этому представлению угла будет соответствовать формула приведения
t g ( π + α + 2 π z ) = t g α
t g 16 π 3 = t g π + π 3 + 2 π · 2 = t g π 3
Воспользовавшись таблицей, укажем значение тангенса
Пример 2. Использование формул приведения
Наконец, для третьего представления угла запишем
Пример 3. Использование формул приведения
Теперь приведем пример на использование формул приведения посложнее
Пример 4. Использование формул приведения
Представим sin 197 ° через синус и косинус острого угла.
Для того, чтобы можно было применять формулы приведения, нужно представить угол α = 197 ° в одном из видов
Теперь посмотрим на формулы приведения для синусов и выберем соответствующие
Мнемоническое правило
1. Аргумент исходной функции представляется в одном из видов
± α + 2 πz π 2 ± α + 2 πz π ± α + 2 πz 3 π 2 ± α + 2 πz
Угол α должен лежать в пределах от 0 до 90 градусов.
2. Определяется знак исходной тригонометрической функции. Такой же знак будет иметь функция, записываемая в правой части формулы.
Чтобы пользоваться мнемоническим праилом для формул приведения нужно уметь определять знаки тригонометрических функций по четвертям единичной окружности. Разберем примеры применения мнемонического правила.
Пример 1. Использование мнемонического правила
А теперь заглянем в формулы, приведенные выше, и убедимся в том, что мнемоническое правило работает.
Пример 2. Использование мнемонического правила
1. Представим углол α = 777 ° в необходимом виде
Теперь рассмотрим пример, который показывает, как важно правильно определить знак тригонометрической функции и правильно представить угол при использовании мнемонического правила. Повторим еще раз.
Угол α должен быть острым!
Пример 3. Использование мнемонического правила
Представим угол α = 5 π 3 в необходимом виде и воспользуемся правилом
Неверный результат обусловлен тем, что угол 2 π 3 не явдяется острым.
Формулы приведения. Доказательство
Первые 16 формул следуют напрямую из свойств основных тригонометрических функций: синуса, косинуса, тангенса и котанганса.
Приведем доказательство формул приведения для синусов и косинусов
С учетом основных тождеств тригонометрии и только что доказанного, можно записать
В доказательстве используются свойства тригонометрических функций с аргументами, противоположными по знаку.
Все остальные формулы приведения можно доказать на базе записанных выше.
Формулы приведения тригонометрических функций
Формулы приведения — это соотношения, которые позволяют перейти от тригонометрических функций синус, косинус, тангенс и котангенс с углами `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.
Формулы приведения: список и таблицы
Всех вместе формул приведения есть 32 штуки. Они несомненно пригодятся на ЕГЭ, экзаменах, зачетах. Но сразу предупредим, что заучивать наизусть их нет необходимости! Нужно потратить немного времени и понять алгоритм их применения, тогда для вас не составит труда в нужный момент вывести необходимое равенство.
Сначала запишем все формулы приведения:
Для угла (`\frac <\pi>2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac <\pi>2 — \alpha)=cos \ \alpha;` ` sin(\frac <\pi>2 + \alpha)=cos \ \alpha`
`cos(\frac <\pi>2 — \alpha)=sin \ \alpha;` ` cos(\frac <\pi>2 + \alpha)=-sin \ \alpha`
`tg(\frac <\pi>2 — \alpha)=ctg \ \alpha;` ` tg(\frac <\pi>2 + \alpha)=-ctg \ \alpha`
`ctg(\frac <\pi>2 — \alpha)=tg \ \alpha;` ` ctg(\frac <\pi>2 + \alpha)=-tg \ \alpha`
Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Для угла (`\frac <3\pi>2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac <3\pi>2 — \alpha)=-cos \ \alpha;` ` sin(\frac <3\pi>2 + \alpha)=-cos \ \alpha`
`cos(\frac <3\pi>2 — \alpha)=-sin \ \alpha;` ` cos(\frac <3\pi>2 + \alpha)=sin \ \alpha`
`tg(\frac <3\pi>2 — \alpha)=ctg \ \alpha;` ` tg(\frac <3\pi>2 + \alpha)=-ctg \ \alpha`
`ctg(\frac <3\pi>2 — \alpha)=tg \ \alpha;` ` ctg(\frac <3\pi>2 + \alpha)=-tg \ \alpha`
Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:
Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.
И вторая, аналогичная таблица, где углы записаны в градусах:
Мнемоническое правило формул приведения или как их запомнить
Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.
Само привило содержит 3 этапа:
Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:
Ответ: ` cos(\pi + \alpha)= — cos \alpha`
2. `sin(\frac <3\pi>2 — \alpha)`.
Ответ: `sin(\frac <3\pi>2 — \alpha)= — cos \alpha`
3. `cos(\frac <7\pi>2 — \alpha)`.
`cos(\frac <7\pi>2 — \alpha)=cos(\frac <6\pi>2+\frac <\pi>2-\alpha)=cos (3\pi+(\frac<\pi>2-\alpha))`. Представим `3\pi` как `2\pi+\pi`. `2\pi` — период функции.
Важно: Функции `cos \alpha` и `sin \alpha` имеют период `2\pi` или `360^\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac<\pi>2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac<\pi>2-\alpha)= — cos (\frac<\pi>2-\alpha)= — sin \alpha`.
Ответ: `cos(\frac <7\pi>2 — \alpha)=- sin \alpha`.
Лошадиное правило
Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?
Итак, мы имеем функции с аргументами `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac <\pi>2`, `\pi`, `\frac <3\pi>2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac <\pi>2` и `\frac <3\pi>2` на вертикальной оси ординат.
Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.
То есть для аргументов с ключевыми точками, расположенными на горизонтальной оси, мы отвечаем «нет», мотая головой в стороны. А для углов с ключевыми точками, расположенными на вертикальной оси, мы отвечаем «да», кивая головой сверху вниз, как лошадь 🙂
Рекомендуем посмотреть видеоурок, в котором автор подробно объясняет, как запомнить формулы приведения без заучивания их наизусть.
Практические примеры использования формул приведения
Применение формул приведения начинается еще в 9, 10 классе. Немало задач с их использованием вынесено на ЕГЭ. Вот некоторые из задач, где придется применять эти формулы:
Пример 1. Вычислите при помощи формул приведения а) `sin 600^\circ`, б) `tg 480^\circ`, в) `cos 330^\circ`, г) `sin 240^\circ`.
Решение: а) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;
б) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac<\sqrt 3>3`;
в) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac<\sqrt 3>2`;
г) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac<\sqrt 3>2`.
Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac <9\pi>8` и `cos \frac <9\pi>8`; 2) `sin \frac <\pi>8` и `cos \frac <3\pi>10`.
Решение: 1)`sin \frac <9\pi>8=sin (\pi+\frac <\pi>8)=-sin \frac <\pi>8`
`cos \frac <9\pi>8=cos (\pi+\frac <\pi>8)=-cos \frac <\pi>8=-sin \frac <3\pi>8`
2) `cos \frac <3\pi>10=cos (\frac <\pi>2-\frac <\pi>5)=sin \frac <\pi>5`
`sin \frac <\pi>8 Доказательство формул приведения
Докажем сначала две формулы для синуса и косинуса аргумента `\frac <\pi>2 + \alpha`: ` sin(\frac <\pi>2 + \alpha)=cos \ \alpha` и` cos(\frac <\pi>2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.
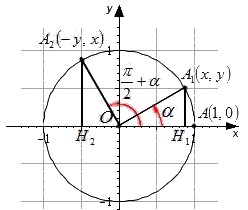
Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на 
угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac <\pi>2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac <\pi>2 + \alpha)=x`, ` cos(\frac <\pi>2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac <\pi>2 + \alpha)=cos \alpha` и ` cos(\frac <\pi>2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac <\pi>2 + \alpha`.
Выходя из определения тангенса и котангенса, получим ` tg(\frac <\pi>2 + \alpha)=\frac
Чтобы доказать формулы с аргументом `\frac <\pi>2 — \alpha`, достаточно представить его, как `\frac <\pi>2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac <\pi>2 — \alpha)=cos(\frac <\pi>2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac <\pi>2 +(\frac <\pi>2+\alpha)` и `\frac <\pi>2 +(\frac <\pi>2-\alpha)` соответственно.
А `\frac <3\pi>2 + \alpha` и `\frac <3\pi>2 — \alpha` как `\pi +(\frac <\pi>2+\alpha)` и `\pi +(\frac <\pi>2-\alpha)`.
Формулы приведения
Тригонометрические тождества — математические выражения для тригонометрических функций, выполняющиеся при всех значениях аргумента (из общей области определения).
Правила преобразования формул приведения.
2) Определяем знак («+» или «-«) значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя.
Формулы приведения.
Закон формул приведения, или как, не заучивая формулы, знать их.
1. Определяем знак функции в нужной четверти.
2. Пользуемся, ниже приведенными, правилами:
Функция меняется на кофункцию.
(синус на косинус либо в обратную сторону, тангенс на котангенс либо в обратную сторону).
Функция на кофункцию НЕ изменяется.
Выше записанные формулы представляют в виде таблицы:
Рассчитать тригонометрические и другие формулы вы можете на нашем инженерном калькуляторе онлайн
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация
Загрузки всякие
Связь
Содержание
Формулы приведения
Формулы приведения косинуса
Формулы приведения синуса
Формулы приведения тригонометрических функций
Мнемоническое правило
Подготовительный шаг: аргумент исходной функции представляется в виде
причем угол должен быть от 0 до 90 градусов (острый). Это замечание про угол альфа очень важно, так как для других углов мнемоническое правило может приводить к неверным результатам.
При приведении функции от аргумента вида kp/2 ± α, где k – целое число, к функции от аргумента α:
Например, при приведении ctg (α – p/2) убеждаемся, что α – p/2 при 0 [синус, косинус]
Правило лошади
Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет своё название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет название.
Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
Формулы приведения в особом доказательстве не нуждаются.
Формулы первой строки выражают свойства четности и нечетности тригонометрических функций, прочие же формулы вытекают из теорем сложения для косинуса и синуса.
В последнем столбце дано геометрическое пояснение формул приведения для острого угла α (равные треугольники заштрихованы).
Формулы четвёртой и восьмой строк легко вывести также и геометрически. Если к углу α прибавить π, т. е. половину полного оборота, то подвижной радиус займёт диаметрально противоположное положение. Абсцисса х и ордината у конца подвижного радиуса, т. е. косинус и синус угла, изменят знаки (не изменяя абсолютной величины) на противоположные, а их отношения не изменятся.
Формулы приведения показывают, что в практических вычислениях достаточно знать значения тригонометрических функций лишь острых углов (и даже не больших 45°).