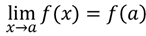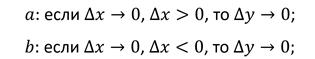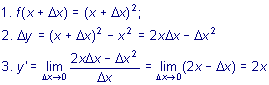Что такое приращение функции и приращение аргумента

Приращение аргумента, приращение функции

Урок 37. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Приращение аргумента, приращение функции»

· познакомиться с понятием непрерывной функции;

· познакомиться с понятием предел функции в точке;

· рассмотреть примеры использования данных понятий для решения задач.

Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Не всегда нам надо знать точные значения тех или иных параметров. Иногда нам достаточно знать, как они изменяются. Например, если мы в течение одного дня выйдем на улицу, то нам не важно, на сколько именно изменилась температура воздуха, а нам важно похолодало или потеплело. Или при движении автомобиля нам, не важно, знать точную скорость, а важно определить разгоняется автомобиль или тормозит.

Причём, если на улице потеплело, то изменения будут со знаком плюс и наоборот если похолодало, то изменения будут со знаком минус.

Если автомобиль разгоняется, то изменения будут со знаком плюс, если тормозит – то со знаком минус.

Для описания таких изменений было введено понятие приращение.

Приращение аргумента обозначают так:

Приращение функции обозначают так:

Давайте рассмотрим, что же такое приращение аргумента и функции на графике.

Рассмотрим ещё один пример.

Давайте вспомним определение непрерывной функции, которое мы формулировали ранее.

Определение непрерывности функции в точке x = a выглядит так:

Определение непрерывности функции в точке можно записать так:

Когда мы вводили определение непрерывной функции, то мы говорили, что функция непрерывна на промежутке X, если она непрерывна в каждой точке промежутка. Давайте уточним, что означает непрерывность функции в концевых точках промежутка, например, как понимать непрерывность функции в точках a и b отрезка [a; b].

Давайте изобразим график линейной функции. Отметим приращение аргумента и функции. И найдём чему равно отношение приращения аргумента к приращению функции.

Источник

Что такое приращение функции и приращение аргумента

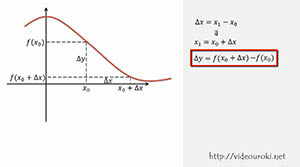
Определение : Пусть функция у = f(x) определена в точках х₀ и х₁. Разность х1 — х₀ называют приращением аргумента (при переходе от точки x₀ к x₁), а разность f(х₁) — f(x₀) называют приращением функции.

Приращение аргумента обозначают ΔX ( дельта икс, Δ — прописная буква греческого алфавита «дельта»; соответствующая строчная буква пишется так: δ). Приращение функции обозначают ΔY или Δ f.

Итак, x1 — x0 = Δ х, значит, х₁ = х0+ Δ x. f(x 1) — f(xо) = Δ у (или Δ f), значит,

Приращение функции в точке — функция обычно обозначаемая от новой переменной определяемая как

Переменная называется приращением аргумента.

В случае когда ясно о каком значении идёт речь, применяется более короткая запись.

Таким образом все эти непонятные иксы, игреки и дельты становятся вполне конкретными точками на плоскости. И мы понимаем,что фраза из определения приращения «Разность х1 — х₀ называют приращением аргумента (при переходе от точки x₀ к x₁), а разность f(х₁) — f(x₀) называют приращением функции» имеет вполне определенный смысл.

Надеюсь, что этот обзор помог вам разобраться с такими непонятными определениями, как приращение функции и приращение аргумента. Для тех же, кто по прежнему ничего не понял, я советую разобраться с такими базовыми понятиями, как функция и аргумент функции.

Источник

Что такое приращение функции и приращение аргумента

рХУФШ ЙНЕЕН ОЕЛПФПТХА ЖХОЛГЙА y= f(x), ПРТЕДЕМЕООХА ОБ ОЕЛПФПТПН РТПНЕЦХФЛЕ. дМС ЛБЦДПЗП ЪОБЮЕОЙС БТЗХНЕОФБ x ЙЪ ЬФПЗП РТПНЕЦХФЛБ ЖХОЛГЙС y = f(x) ЙНЕЕФ ПРТЕДЕМЕООПЕ ЪОБЮЕОЙЕ.

уПУФБЧЙН ПФОПЫЕОЙЕ РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ

оБКДЕН РТЕДЕМ ЬФПЗП ПФОПЫЕОЙС РТЙ . еУМЙ ЬФПФ РТЕДЕМ УХЭЕУФЧХЕФ, ФП ЕЗП ОБЪЩЧБАФ РТПЙЪЧПДОПК ДБООПК ЖХОЛГЙЙ f(x) Ч ФПЮЛЕ x 0 Й ПВПЪОБЮБАФ f ‘( x 0 ). йФБЛ,

рТПЙЪЧПДОБС ПВПЪОБЮБЕФУС УЙНЧПМБНЙ f ‘ (x), y ‘, . лПОЛТЕФОПЕ ЪОБЮЕОЙЕ РТПЙЪЧПДОПК РТЙ x = a ПВПЪОБЮБЕФУС f ‘( a ) ЙМЙ .

пРЕТБГЙС ОБИПЦДЕОЙС РТПЙЪЧПДОПК ПФ ЖХОЛГЙЙ f(x) ОБЪЩЧБЕФУС ДЙЖЖЕТЕОГЙТПЧБОЙЕН ЬФПК ЖХОЛГЙЙ.

дМС ОЕРПУТЕДУФЧЕООПЗП ОБИПЦДЕОЙС РТПЙЪЧПДОПК РП ПРТЕДЕМЕОЙА НПЦОП РТЙНЕОЙФШ УМЕДХАЭЕЕ РТБЛФЙЮЕУЛПЕ РТБЧЙМП :

рТЙНЕТ 1

оБКФЙ РТПЙЪЧПДОХА ЖХОЛГЙЙ y = x 2

Б) Ч РТПЙЪЧПМШОПК ФПЮЛЕ;

a)

рТЙНЕТ 2

йУРПМШЪХС ПРТЕДЕМЕОЙЕ, ОБКФЙ РТПЙЪЧПДОХА ЖХОЛГЙЙ Ч РТПЙЪЧПМШОПК ФПЮЛЕ.

Источник

Приращение аргумента. Приращение функции

Описание презентации по отдельным слайдам:

Описание слайда:

Приращение аргумента.
Приращение функции.
МБОУ лицей №10 города Советска
Калининградской области
учитель математики
Разыграева Татьяна Николаевна

Описание слайда:

При сравнении значения функции f в некоторой фиксированной точке x₀ со значениями этой функции в различных точках x, лежащих в окрестности x₀, удобно выражать разность f(x) – f(x₀) через разность x – x₀, пользуясь понятиями «приращение аргумента» и «приращение функции».
Пусть x – произвольная точка, лежащая в некоторой окрестности фиксированной точки x₀. Разность x – x₀ называется приращением независимой переменной ( или приращением аргумента) в точке x₀ и обозначается Δx. Таким образом,
Δx = x –x₀
откуда следует, что
x = x₀ + Δx.

Описание слайда:

Говорят также, что первоначальное значение аргумента x₀ получило приращение Δx. Вследствие этого значение функции f изменится на величину
f(x) – f(x₀) = f (x₀ +Δx) – f(x₀).
Эта разность называется приращением функции f в точке x₀, соответствующим приращению Δx, и обозначается символом Δf (читается «дельта эф»), т.е. по определению
Δf = f (x₀ + Δx) – f (x₀)
откуда

f (x) = f (x₀ +Δx) = f (x₀) + Δf.

Описание слайда:

Описание слайда:

Функция y = f(x) непрерывна в точке
х = а, если в точке х = а выполняется
следующее условие:
если  х  0, то  у  0.
Пример № 2.
Для функции y = kx + m найти: а) приращение функции
при переходе от фиксированной точки х к точке х +  х;
б) предел отношения приращения функции к приращению
аргумента, при условии, что приращение аргумента
стремится к нулю.
Решение.

Описание слайда:

Имеем:
f(x) = kx + m
f(x + x) = k(x + x) + m
y = f(x + x) – f(x) = (k(x + x) + m) – (kx + m)
y = (kx + kx + m) – (kx + m) = k·x.
y = k·x.
Имеем:

Описание слайда:

Описание слайда:

Описание слайда:

Итак, для заданной функции y = x² получили:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Курс профессиональной переподготовки

Охрана труда

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Курсы повышения квалификации «Организация деятельности педагогических работников по классному руководству» 17 ч.

Презентация к исследованию «Образование Верещакского Дома Культуры»

Исследовательская работа «Образование Верещакского Дома Культуры»

«Плюсы и минусы дистанционного обучения»

Текст выступления на семинаре к презентации «Музыка нас связала»

Презентация на тему «Музыка нас связала!»

Реферат «Типология синтаксических систем. Типы предложений в сопоставляемых языках.»»

Презентация по ПМ 03. МДК 03.02 на тему «Графики работы водителей»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5357175 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В Москве новогодние утренники в школах и детсадах пройдут без родителей

Время чтения: 1 минута

В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения

Время чтения: 1 минута

Трехлетнюю олимпиаду среди школ запустят в России в 2022 году

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Путин поручил разработать концепцию развития допобразования детей до 2030 года

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Урок по теме: «Приращение функции»

Не всегда в жизни нас интересуют точные значения каких-либо величин. Иногда интересно узнать изменение этой величины, например, средняя скорость автобуса, отношение величины перемещения к промежутку времени и т.д. Для сравнения значения функции в некоторой точке со значениями этой же функции в других точках, удобно использовать такие понятия, как «приращение функции» и «приращение аргумента».

Понятия «приращение функции» и «приращение аргумента»

Если мы изменяем аргумент, то и значение функции тоже будет изменяться.

Приращением функции f в точке x ₀ , соответствующим приращению ∆х называется разность f(x ₀ + ∆х) – f(x ₀ ). Приращение функции обозначается следующим образом ∆f. Таким образом получаем, по определению:

Иногда, ∆f еще называют приращением зависимой переменной и для обозначения используют ∆у, если функция была, к примеру, у=f(x).

Геометрический смысл приращения

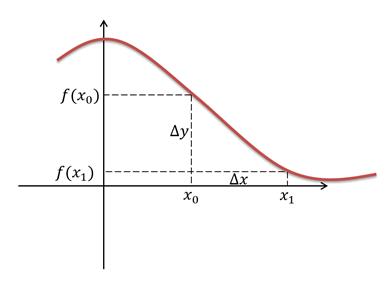
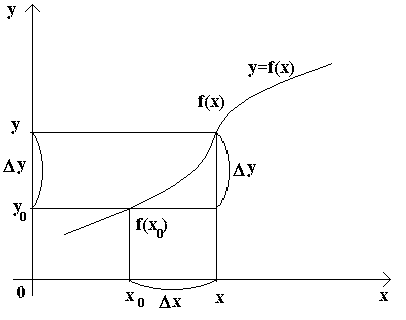
Посмотрите на следующий рисунок.

Как видите, приращение показывает изменение ординаты и абсциссы точки. А отношение приращения функции к приращению аргумента определяет угол наклона секущей, проходящей через начальное и конечное положение точки.

Рассмотрим примеры приращения функции и аргумента

Воспользуемся формулами, приведенными выше:

∆ f=f(2.1) – f(2) = 2.1 2 – 2 2 = 0.41.

Опять же, воспользуемся формулами, полученными выше.

Пример 3. . Найти приращение функции y=2x 2 при x0=3 и Δx=0,1

Решение. Подставляя в формулу, получаем, что приращение функции:

Δy=y(3+0,1)−y(3)=2 ⋅ (3+0,1) 2 −2 ⋅ 3 2 =1,22

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1547378

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения

Время чтения: 1 минута

Каждый третий российский школьник хотел бы стать разработчиком игр

Время чтения: 2 минуты

Школьники из России выиграли 8 медалей на Международном турнире по информатике

Время чтения: 3 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

ДНР полностью перешла на стандарты и программы России в образовании

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник