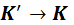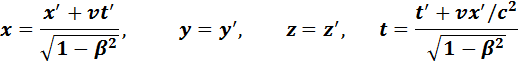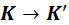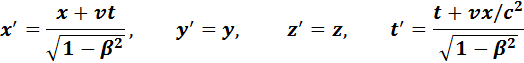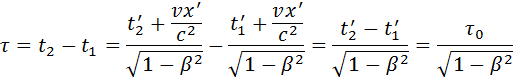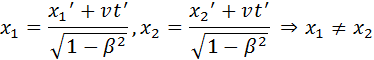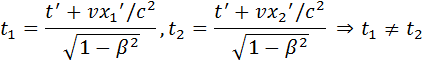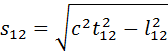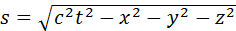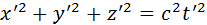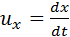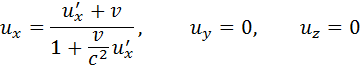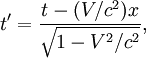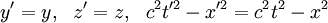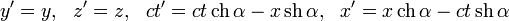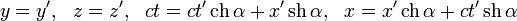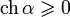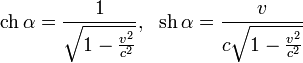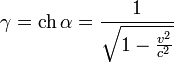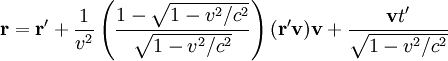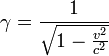Что такое преобразования лоренца

Преобразования Лоренца

Классические преобразования Галилея несовместимы с постулатами СТО и, следовательно, должны быть заменены. Эти новые преобразования должны установить связь между координатами (x, y, z) и моментом времени t события, наблюдаемого в системе отсчета K, и координатами (x’, y’, z’) и моментом времени t’ этого же события, наблюдаемого в системе отсчета K’.

Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K’ движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:

Из преобразований Лоренца вытекает целый ряд следствий. В частности, из них следует релятивистский эффект замедления времени и лоренцево сокращение длины. Пусть, например, в некоторой точке x’ системы K’ происходит процесс длительностью τ₀ = t’₂ – t’₁ (собственное время), где t’₁ и t’₂ – показания часов в системе K’ в начале и конце процесса. Длительность τ этого процесса в системе K будет равна

Аналогичным образом, можно показать, что из преобразований Лоренца вытекает релятивистское сокращение длины. Одним из важнейших следствий из преобразований Лоренца является вывод об относительности одновременности. Пусть, например, в двух разных точках системы отсчета K’ (x’₁ ≠ x’₂) одновременно с точки зрения наблюдателя в K’ (t’₁ = t’₂ = t’) происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь

Следовательно, в системе K эти события, оставаясь пространственно разобщенными, оказываются неодновременными. Более того, знак разности t₂ – t₁ определяется знаком выражения υ(x’₂ – x’₁), поэтому в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Этот вывод СТО не относится к событиям, связанным причинно-следственными связями, когда одно из событий является физическим следствием другого. Можно показать, что в СТО не нарушается принцип причинности, и порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.

Относительность одновременности пространственно-разобщенных событий можно проиллюстрировать на следующем примере.

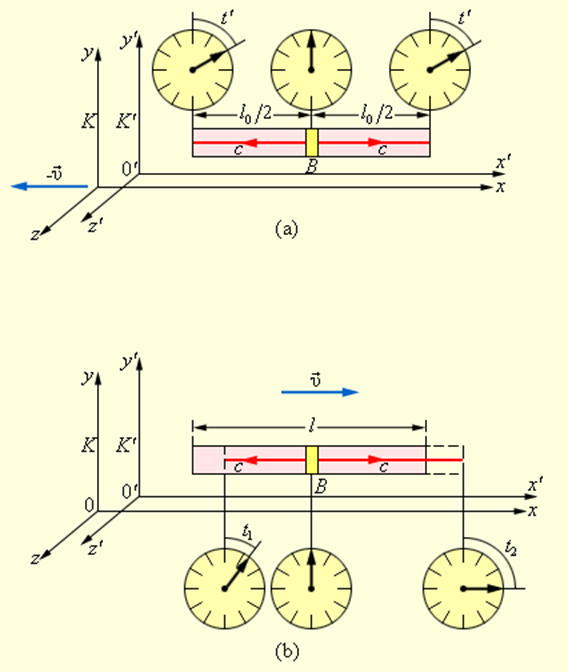
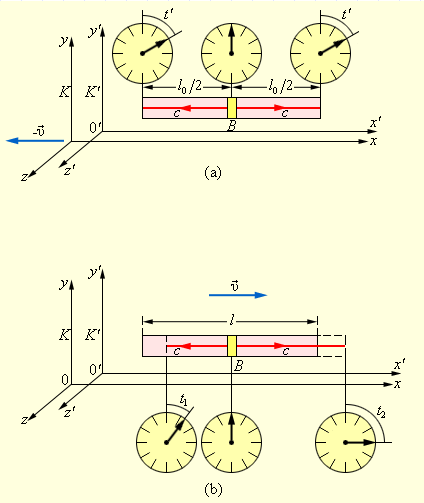
Пусть в системе отсчета K’ вдоль оси x’ неподвижно расположен длинный жесткий стержень. В центре стержня находится импульсная лампа B, а на его концах установлены двое синхронизированных часов(рис. 4.4.1(a)), система K’ движется вдоль оси x системы K со скоростью υ. В некоторый момент времени лампа посылает короткие световые импульсы в направлении концов стержня. В силу равноправия обоих направлений свет в системе K’ дойдет до концов стержня одновременно, и часы, закрепленные на концах стержня, покажут одно и то же время t’. Относительно системы K концы стержня движутся со скоростью υ так, что один конец движется навстречу световому импульсу, а другой конец свету приходится догонять. Так как скорости распространения световых импульсов в обоих направлениях одинаковы и равны c, то, с точки зрения наблюдателя в системе K, свет раньше дойдет до левого конца стержня, чем до правого (рис. 4.4.1(b)).

Относительность одновременности. Световой импульс достигает концов твердого стержня одновременно в системе отсчета K’ (a) и не одновременно в системе отсчета K (b)

Преобразования Лоренца выражают относительный характер промежутков времени и расстояний. Однако, в СТО наряду с утверждением относительного характера пространства и времени важную роль играет установление инвариантных физических величин, которые не изменяются при переходе от одной системы отсчета к другой. Одной из таких величин является скорость света в вакууме c, которая в СТО приобретает абсолютный характер. Другой важной инвариантной величиной, отражающей абсолютный характер пространственно-временных связей, является интервал между событиями.

Пространственно-временной интервал определяется в СТО следующим соотношением:

где t₁₂ – промежуток времени между событиями в некоторой системе отсчета, а l₁₂ – расстояние между точками, в которых происходят рассматриваемые события, в той же системе отсчета. В частном случае, когда одно из событий происходит в начале координат (x₁ = y₁ = z₁ = 0) системы отсчета в момент времени t₁ = 0, а второе – в точке с координатами x, y, z в момент времени t, пространственно-временной интервал между этими событиями записывается в виде

С помощью преобразований Лоренца можно доказать, что пространственно-временной интервал между двумя событиями не изменяется при переходе из одной инерциальной системы в другую. Инвариантность интервала означает, что, несмотря на относительность расстояний и промежутков времени, протекание физических процессов носит объективный характер и не зависит от системы отсчета.

Если одно из событий представляет собой вспышку света в начале координат системы отсчета при t = 0, а второе – приход светового фронта в точку с координатами x, y, z в момент времени t (рис. 4.1.3), то

и, следовательно, интервал для этой пары событий s = 0. В другой системе отсчета координаты и время второго события будут другими, но и в этой системе пространственно-временной интервал s’ окажется равным нулю, так как

Для любых двух событий, связанных между собой световым сигналом, интервал равен нулю.

Из преобразований Лоренца для координат и времени можно получить релятивистский закон сложения скоростей. Пусть, например, в системе отсчета K’ вдоль оси x’ движется частица со скоростью 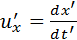Составляющие скорости частицы u’x и u’z равны нулю. Скорость этой частицы в системе K будет равна

С помощью операции дифференцирования из формул преобразований Лоренца можно найти:

Эти соотношения выражают релятивистский закон сложения скоростей для случая, когда частица движется параллельно относительной скорости 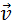систем отсчета K и K’.

Источник

Преобразования Лоренца

Преобразования Лоренца представляют собой кинематические формулы, с помощью которых происходит преобразование координат и времени в специальной теории относительности.

Они были впервые сформулированы еще в 1904 году в качестве преобразований, относительно которых были инвариантны уравнения электродинамики.

Используя эти формулы, мы можем вывести из них множество следствий. Так, именно из системы преобразований Лоренца следует лоренцево сокращение длины и релятивистский эффект замедления времени.

Формула релятивистского сокращения длины выводится из преобразований Лоренца точно таким же образом.

Принцип относительности одновременности

Еще одно важное следствие, которое необходимо знать, – это положение о том, что любая одновременность относительна.

Например, если в системе отсчета K ‘ взять две разные точки, в которых некий процесс будет протекать одновременно (с позиции стороннего наблюдателя), то в системе наблюдатель будет иметь следующее:

Если между событиями имеется причинно-следственная связь, то данный вывод специальной теории относительности для них использовать нельзя. Однако мы можем показать, что при этом не нарушается принцип причинности, и события следуют в нужном порядке в любой инерциальной системе отсчета.

Разберем пример, показывающий, что одновременность разобщенных в пространстве событий является относительной.

Инвариантные величины в СТО

Данные преобразования нужны нам для выражения относительного характера временных промежутков и промежутков расстояний. Вместе с тем в специальной теории относительности помимо утверждения относительного характера времени и пространства очень важно установить инвариантные физические величины, не изменяющиеся при смене системы отсчета. Подобной величиной является скорость света в вакууме, чей характер в рамках СТО становится абсолютным. Также важна такая величина, как интервал между событиями, поскольку именно она выражает абсолютность пространственно-временной связи.

Для вычисления пространственно-временного интервала необходимо использовать следующую формулу:

Преобразования Лоренца дают нам возможность доказать неизменность пространственно-временного интервала между событиями при смене инерциальной системы.

Если величина интервала не зависит от того, какая система отсчета используется, т.е. является объективной при любых относительных расстояниях и временных промежутках, то такой интервал называется инвариантным.

У нас получилось, что интервал этой пары событий будет равен нулю. Если мы поменяем систему координат и возьмем другое время для второго события, то результаты окажутся точно такими же, поскольку:

x 2 + y 2 + z 2 = c 2 t 2

Иначе говоря, любые два события, которые связывает между собой световой сигнал, будут иметь нулевой пространственно-временной интервал.

Также формулы Лоренца для времени и координат можно использовать для выведения релятивистского закона сложения скоростей.

Применим к одной из формул преобразования Лоренца операцию дифференцирования и получим следующее:

Источник

Преобразование Лоренца

Преобразованиями Лоренца в физике, в частности в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты (x,y,z,t) каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.

Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца.

Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца.

С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.

Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.

Содержание

Вид преобразований при коллинеарных (параллельных) пространственных осях

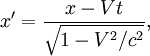
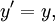
Эта форма преобразования (то есть при выборе коллинеарных осей), называемое иногда бустом (англ. boost ) или лоренцевским бустом (особенно в англоязычной литературе), несмотря на свою простоту включает, по сути, всё специфическое физическое содержание преобразований Лоренца, так как пространственные оси всегда можно выбрать таким образом, а при желании добавить пространственные повороты не представляет трудности (см. это в явном развёрнутом виде ниже), хотя и делает формулы более громоздкими.

Вывод преобразований

Преобразования Лоренца могут быть получены абстрактно, из групповых соображений (в этом случае они получаются с неопределённым c ), как обобщение преобразований Галилея (что было проделано Пуанкаре — см. ниже). Однако впервые были получены как преобразования, относительно которых ковариантны уравнения Максвелла (то есть по сути — которые не меняют законов электродинамики и оптики). Могут также быть получены из предположения линейности преобразований и постулата одинаковости скорости света во всех системах отсчёта (являющегося упрощённой формулировкой требования ковариантности электродинамики относительно искомых преобразований, и распространением принципа равноправия инерциальных систем отсчёта — принципа относительности — на электродинамику), как это делается в специальной теории относительности (СТО) (при этом c в преобразованиях Лоренца получается определённым и совпадает со скоростью света).

Надо заметить, что если не ограничивать класс преобразований координат линейными, то первый закон Ньютона выполняется не только для преобразований Лоренца, а для более широкого класса дробно-линейных преобразований (однако этот более широкий класс преобразований — за исключением, конечно, частного случая преобразований Лоренца — не сохраняет метрику постоянной).

Алгебраический вывод

На основании нескольких естественных предположений (основным из которых является предположение о существовании принципиально максимальной скорости распространения взаимодействий) можно показать, что при смене ИСО должна сохраняться величина

Мы будем искать линейные преобразования Лоренца, так как при бесконечно малых преобразованиях координат дифференциалы новых координат линейно зависят от дифференциалов старых координат, а в силу однородности пространства и времени коэффициенты не могут зависеть от координат, только от взаимной ориентации и скорости ИСО.

Наиболее общий вид таких преобразований:

где α — некоторый параметр, называемый быстротой. Обратные преобразования имеют вид

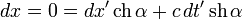
Учитывая, что при смене ИСО не должна меняться ориентация пространства, получим что

Следовательно, уравнение для быстроты однозначно разрешимо:

а преобразования Лоренца имеют вид

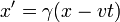
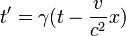
Группа симметрий уравнений Максвелла

Наглядный вывод преобразований Лоренца

Примем постулаты СТО, сводящиеся к расширенному принципу относительности, утверждающему, что все физические процессы протекают в точности одинаково во всех инерциальных системах отсчета (уточняющий его принцип постоянства скорости света в СТО означает расширение принципа относительности на электродинамику вместе с уточняющим утверждением о том, что нет никакой фундаментальной физической среды (эфира), которая выделяла бы одну из систем отсчета на опыте — то есть если даже эфир и есть, то его наличие не должно никак нарушать принципа относительности на практике). Кроме того, полезно явно подчеркнуть, что принцип постоянства скорости света означает наличие именно конечной скорости (скорости света), заложенной в фундаментальные законы (уравнения), одной и той же для всех инерциальных систем отсчета, причём и в каждой системе отсчета величина скорости света одинакова для любых направлений его распространения (это используется ниже).

Преобразование для поперечных осей (п.1)

Пусть есть две бесконечные плоскости, перпендикулярные оси y. Расстояние между этими плоскостями очевидно не должно зависеть от скорости движения плоскостей вдоль самих себя (то есть переходя в себя же), а значит — не зависит от выбора системы отсчета среди движущихся вдоль оси x. (Чтобы быть совсем уверенным в этом, можно провести мысленный эксперимент, заключающийся в измерении времени, требующегося лучу света, движущемуся вдоль y в каждой такой системе отсчета, для того, чтобы, стартовав на одной плоскости, достичь второй, и увидеть, что такое время очевидно будет одинаковым, если верны постулаты СТО).

То же самое, конечно, верно и для оси z. Поэтому, исключив для простоты физически неинтересный случай поворота координат второй системы относительно первой на постоянный (независящий от времени) угол, получаем:

Замедление времени (п.2)

Показать, что любые процессы (например ход часов) выглядит медленнее из системы отсчета где носитель этого процесса (например часы) движется, чем в его собственной системе отсчета (в которой он неподвижен), и найти количественно фактор такого замедления, можно, рассмотрев мысленный эксперимент со «световыми часами», представляющими собой источник и приемник света, удаленные друг от друга на известное фиксированное расстояние L, и отмеряющие, таким образом, интервал времени L/c, соответствующий времени прохождения света от источника до приемника (это можно непрерывно повторять). Все другие часы, из принципу относительности, должны идти точно так же.

Для более прямого соответствия формы полученного результата формуле прямого преобразования Лоренца, будем считать, что наши световые часы покоятся в нештрихованой системе отсчета K, штрихованая же система отсчета K’ пусть движется для определенности вправо вдоль оси x со скоростью V. Источник и приемник расположим вдоль оси y при x=0. Это частный случай, который позволит нам получить сперва отдельно частное и более простое преобразование для времени.

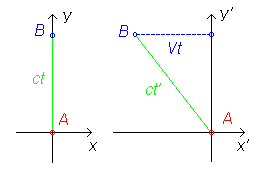
Поместим источник в начальный момент времени в начало координат, обозначив его A (см. рисунок, там он изображен красной точкой), а приемник обозначим B (синяя точка). В нештрихованой системе отсчета (на рисунке слева) импульс света летит точно по оси y (B, как и A в этой системе неподвижны). Таким образом, от излучения до поглощения света в этой системе проходит время .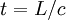

В штрихованой же системе отсчета точки A и B движутся влево со скоростью V. Особенно нас интересует движение точки B, обозначенное на рисунке пунктиром. Из-за этого ее смещения, равного 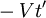, свету в этой системе отсчета приходится пройти не расстояние L, а большее (на рисунке путь света от A к B изображен зеленой линией). Это расстояние нетрудно выразить с помощью теоремы Пифагора, и оно же равно ct’, откуда:

а учитывая упомянутые чуть выше L = ct и выражая t’ через t, имеем:

,

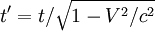
что и является преобразованием Лоренца для времени для условия x = 0.

(по сути же это есть замедление времени при наблюдении часов — или любого другого процесса с локальным носителем — из системы отсчета, движущейся относительно него: мы видим, что t’ > t).

Относительность одновременности (п.3)

Кроме замедления времени в движущейся системе отсчета (замедления хода всех часов движущейся лаборатории при наблюдении их из неподвижной), оказывается, что начало отсчета времени в движущейся системе отсчета также не совпадает с таковым в неподвижной, причем сдвиг этого начала отсчета — разный в разных точках — зависит от x (часы, выглядящие синхронными в своей собственной системе отсчета, выглядят идущими с разным опережением-отставанием, зависящим от их пространственного расположения, если на них смотреть из другой системы отсчета, такой, в которой их собственная система отсчета движется).

Чтобы стало понятным само существо проблемы, придется так или иначе обдумать вопрос, а что значит, что часы в разных удаленных друг от друга точках пространства (например, в разных городах) идут одинаково (синхронно), как в этом можно убедиться, или как (с помощью какой процедуры) можно синхронизировать часы в разных местах, если изначально они не были синхронны.

Уже простейший способ синхронизации, заключающийся в том, что все часы синхронизируют в одном месте, а затем переносят в разные точки, позволяет качественно убедиться в том, что часы, синхронизированные в одной системе отсчета, будут выглядеть показывающими разное время из другой системы отсчета. Дело в том, что для часов, которые мы переносим вправо по оси x и влево по оси x, — время будет замедляться по-разному, так как их скорость будет обязательно различной в этой другой системе отсчета.

Это можно было бы аккуратно рассмотреть количественно, получив так искомый здесь результат. Но более просто этого достичь позволяет рассмотрение синхронизации с помощью световых сигналов (а принцип относительности говорит, что любой корректный способ синхронизации должен дать один и тот же результат, в чём, впрочем, при желании можно убедиться и явно).

Итак, рассмотрим синхронизацию с помощью световых сигналов. Этот процесс может заключаться, например, в обмене световыми сигналами между двумя удаленными хронометрами: если сигналы испущены в одно и то же время, то до получения сигнала по каждым часам пройдет одно и то же время. Но еще проще несколько другой (эквивалентный этому) способ: можно точно в середине отрезка, соединяющего хронометры, произвести вспышку света, и утверждать, что свет придет к обоим хронометрам одновременно.

В собственной системе отсчета (в которой хронометры неподвижны) картина симметрична. Однако в любой другой системе отсчета оба хронометра движутся (для определенности будем считать, что вправо), и тогда свету от середины отрезка, соединяющего их в начальный момент, потребуется меньше времени, чтобы дойти до левого хронометра (движущегося навстречу свету), чем до правого (который импульс света должен догонять).

Таким образом, хронометры, синхронные в своей собственной системе отсчета, по часам другой системы отсчета выглядят несинхронными. А это и означает, что события, одновременные в одной системе отсчета, неодновременны в другой. Это и называется относительностью одновременности.

Несложные геометрические выкладки позволяют (изобразив движение световых импульсов и хронометров на плоскости xt), получить выражение для сдвига начала отсчета времени:

Таким образом, сводя вместе результаты пунктов 1 и 2, получаем для преобразования времени

.

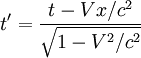
Лоренцевское сокращение длины (п.4)

Рассмотрев движение светового импульса вдоль оси x (а не вдоль y, как было в п.1), и потребовав (на основании постулата одинаковости скорости света во всех инерциальных системах отсчёта), чтобы расстояние между двумя точками было всегда равно времени, за которое свет идёт от одной точки до другой, делённому на (константу) скорость света, можно получить фактор сокращения расстояний вдоль оси x, а учитывая, что смещение начала отсчёта − Vt очевидно, можно получить и преобразование для x:

.

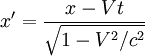
Однако ещё проще теперь понять, что x‘ выражается именно таким образом, заметив, что в плоскости x − ct график движения [1] импульса света должен быть прямой, наклонённой под 45° (из-за того, что скорость света — всегда c), а значит и масштаб по x и по ct должен быть одинаковым, а выражения в системе единиц c = 1 — симметричными.

Разные формы записи преобразований

Вид преобразований при произвольной ориентации осей

В силу произвольности введения осей координат, многие задачи можно свести к указанному случаю. Если же задача требует иного расположения осей, то можно воспользоваться формулами преобразований в более общем случае. Для этого радиус-вектор точки

,

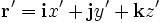
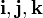
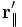
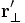
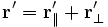
где — орты, надо разбить на составляющую параллельную скорости и составляющую ей перпендикулярную

.

Тогда преобразования получат вид

,

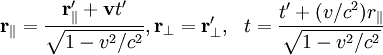
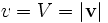
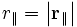
где — абсолютная величина скорости, — абсолютная величина продольной составляющей радиус-вектора.

Эти формулы для случая параллельных осей, но с произвольно направленной скоростью, можно преобразовать к виду, впервые полученному Герглоцем:

.

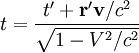
Обратите внимание, что самый общий случай, когда начала координат не совпадают в нулевой момент времени, здесь не приведён с целью экономии места. Его можно получить, добавив к преобразованиям Лоренца трансляцию (смещение начала координат).

Преобразования Лоренца в матричном виде

Для случая коллинеарных осей преобразования Лоренца записываются в виде

,

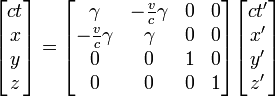
где .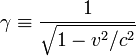

При произвольной ориентации осей, в форме 4-векторов это преобразование записывается как:

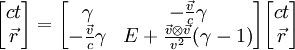
где E — единичная матрица 33, — тензорное умножение трехмерных векторов.

Произвольное однородное преобразование Лоренца можно представить как некоторую композицию вращений пространства и элементарных преобразований Лоренца, затрагивающих только время и одну из координат. Это следует из алгебраической теоремы о разложении произвольного вращения на простые.

Свойства преобразований Лоренца

(убедиться в этом нетрудно, например, убедившись явно в том, что матрица преобразования Лоренца L — ортогональна в смысле метрики, определяемой таким выражением, то есть если 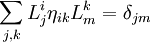, что проще всего проверить для буста, для трехмерных же вращений это очевидно, следовательно, верно и для любых их композиций; как только мы узнали, что преобразования ортогональны, значит расстояние, вычисленное в такой метрике, неизменно в любой системе координат — по свойству ортогональных преобразований).

Связанные определения

Лоренц-инвариантность — свойство физических законов записываться одинаково во всех инерциальных системах отсчета(с учетом преобразований Лоренца). Принято считать, что этим свойством должны обладать все физические законы, и экспериментальных отклонений от него не обнаружено. Однако некоторые теории пока не удаётся построить так, чтобы выполнялась Лоренц-инвариантность.

История

Преобразования названы в честь их первооткрывателя — Х. А. Лоренца, который впервые ввел их (вместо преобразований Галилея) в качестве преобразований, связывающих геометрические величины (длины, углы), измеренных в разных инерциальных системах отсчета, чтобы устранить противоречия между электродинамикой и механикой, которые имелись в ньютоновской формулировке, включающей преобразования Галилея, что в конечном итоге привело к успеху при существенной модификации механики.

Сначала было обнаружено, что уравнения Максвелла инвариантны относительно этих преобразований (В. Фогтом в 1887 г.). Это же было повторено Лармором в 1900 г..

В 1892 г. Лоренц ввёл теорию сокращения, предполагающую сокращение длин всех твёрдых тел в направлении движения, количественно совпадающее с тем, что понимается сейчас под лоренцевым сокращением.

Преобразования Лоренца были впервые опубликованы в 1904 г. но в то время их форма была несовершенна. К современному, полностью самосогласованному виду их привёл французский математик А. Пуанкаре. Только в 1905 г. Пуанкаре и затем Эйнштейн в своей теории относительности пришёл к широко популярной впоследствии формально-аксиоматической трактовке этих преобразований. Пуанкаре же ввел термины «преобразования Лоренца» и «группа Лоренца», показал, исходя из эфирной модели, невозможность обнаружить движение относительно абсолютной системы отсчета (системы, в который эфир неподвижен), модифицировав таким образом принцип относительности Галилея. Ему же принадлежит групповой вывод явного вида преобразований Лоренца (с неопределенным c) без независимого постулата инвариантности скорости света.

Источник