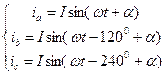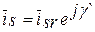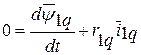Что такое преобразование парка горева

Уравнения Парка – Горева для синхронной машины.

Уравнения Парка — Горева связывают между собой мгновенные значения токов, магнитных пото­ков, напряжений в осях координат (d, q), связанных с ротором.

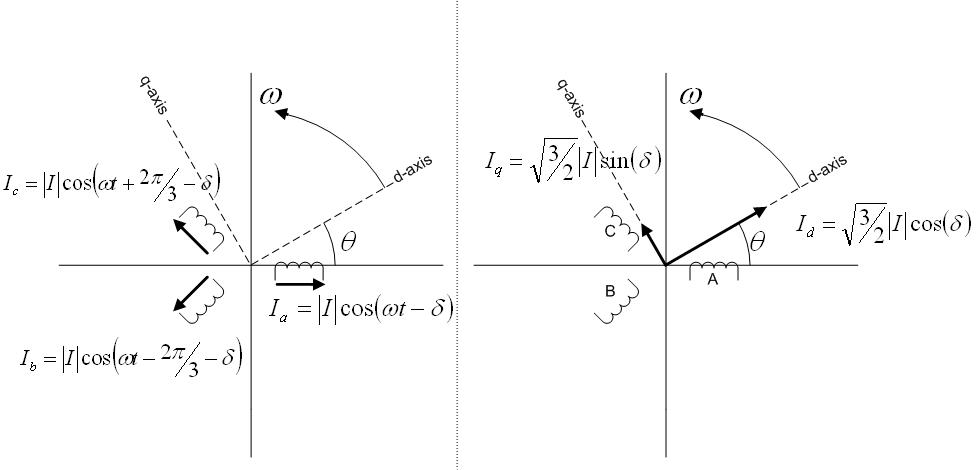
Мгновенные значения параметров режима опре­деляют как проекции на оси времени фаз а, b, с вектора тока (напряжения, ЭДС, потокосцепления), вращающегося с угловой ско­ростью . Этот вектор тока называют обобщенным.

Оси времени t_a, t_b, t_c фаз a, b, с неподвижны и совпадают с осями обмоток статора (рис. 2.1). Мгновенные значения фазных токов равны:

где — произвольный угол.

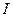
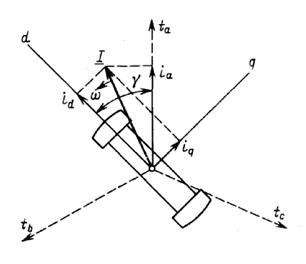
Рис.2.1 Обобщенный вектор тока и его проекции на временные оси.

Проекции обобщенного вектора тока на оси d, q, связанные с ротором, дают значения продольного и поперечного токов (рис. 2.2):

При наличии токов нулевой последовательности

Соотношения, аналогичные приведенным выше, справедливы для напряжений, ЭДС и потокосцеплений.

Рис. 2.2. Обобщенный вектор тока I и проекции его

на продольную и поперечную оси ротора

Связь между мгновенными значениями фазных величин и величин в продольной и поперечной осях устанавливается на основе уравнений:

Угол меняется во времени:

где — полное потокосцепление статора в продольной и поперечной осях.

В случаях симметричного режима энергосистемы токи нулевой последовательности отсутствуют ( = 0).

Значения потокосцепления статора в поперечной и продольных осях определяются из вы­ражений:

= G (р) U_f + X_d (р) i_d

= X_q (p) ,

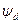
где G(p)—операторная проводимость маши­ны;

X_d(p), X_q(p) — операторные сопротивления машины в продольной и поперечной осях;

U_f — напряжение возбуждения машины.

Для машины без демпферных обмоток и эквивалентных им контуров:

;

;

.

Если известна ЭДС 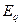, то

,

где — постоянная времени обмотки возбуждения машины при разомкнутой обмотке статора;

— активное сопротивление обмотки статора по продольной оси;

— реактивное сопротивление взаимной индукции обмотки возбуждения со статором в продольной оси;

— реактивное сопротивление индуктивности ротора в продольной оси.

Для машины с демпферными обмотками значения потокосцепления статора в поперечной и продольных осях 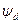и определяются теми же уравнениями.

Рис.2.3 Основные параметры синхронной машины для принятых направлений осей.

Уравнения Парка – Горева для принятых на рис.2.3. направлениях осей примут вид:

;

;

;

где 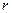— активное сопротивление статора;

— активное сопротивление статора нулевой последовательности;

; ;

.

В системе относительных единиц , поэтому .

Третье уравнение системы относится к слу­чаю несимметричного режима или несиммет­ричной схемы.

Уравнения, приведенные выше, полностью описывают переходный процесс машины, ра­ботающей на шины неизменного напряжения. Для анализа переходного процесса в сложной энергосистеме уравнения составляются для каждого эле­мента (генераторов, нагрузок, участков сети) и решаются совместно.

Решение системы урав­нений Парка – Горева относительно токов или других величин, рассматриваемых как неизвестные, проводится в операторной форме (для изобра­жений), например находятся значения токов

; ;

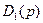
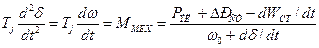
где , D₂ (p) — миноры определителя систе­мы; D (р) — главный определитель системы.

,

где — постоянная инерции машины.

Для определения параметров при переходных процессах можно использовать упрощенные уравнения Парка – Горева. Для получения этих уравнений отказы­ваются от учета влияния:

1) апериодической составляющей тока ста­тора (трансформаторной ЭДС);

2) периодических токов ротора, связанных с апериодическими составляющими тока ста­тора;

3) активного сопротивления в цепи ста­тора.

; .

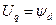
Данные уравнения положены в основу рас­четов периодической составляющей токов короткого замыкания при обычно принимаемых допущениях.

При принятых предпосылках отдаваемая мощность численно равна вращающемуся моменту; поэтому для симметричного режима или режима, условно приведённого к симметричному,

.

Уравнение относительного движения ротора

.

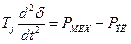
На основе этих расчетных уравнений (их иногда называют уравнениями Лонглея или уравнениями Лебедева — Жданова) обычно ведутся проектные и эксплуатацион­ные расчеты устойчивости. Они позволяют для расчетов переходных процессов пользоваться соотношениями, вытекающими из векторной диаграммы установившегося режима [рис.2.1].

Источник

Уравнения Парка-Горева синхронной машины

Уравнение электрического равновесия цепи статора, записанное через изображающие векторы напряжений, токов и потокосцеплений в неподвижной системе координат, имеет вид

где ;

w_с – угловая частота напряжения, которая при работе синхронного генератора параллельно с системой неограниченной мощности равна синхронной.

Это же уравнение в системе координат, вращающейся со скоростью ротора w_r, получим, используя выражение для перехода изображающего вектора во вращающейся системы координат к неподвижной, которое, например, для тока имеет вид

где — изображающий вектор тока статора в неподвижной системе координат;

— изображающий вектор тока статора во вращающейся системе координат;

— угол между магнитной осью фазы А и осью d ротора.

,

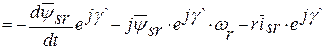
т.к. .

В результате, в системе d, q, 0, вращающейся со скоростью ротора w_r, уравнение равновесия цепи статора, записанное через изображающие векторы, имеет вид

.

Уравнения равновесия напряжений ротора

,

,

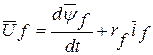
при этом остаются неизменными, так как входящие в него величины с самого начала определялись именно в системе координат ротора.

Выразим изображающие векторы через их составляющие по осям вращающейся комплексной плоскости, помня, что действительная ось комплексной плоскости направлена вдоль оси d, а мнимая ― вдоль отрицательного направления оси q. В результате получаем :

,

,

,

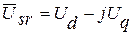
Подставив эти выражения в выражение для , получим:

.

Приравнивая отдельно действительные и мнимые части, получим

,

,

,

, (4.1)

,

.

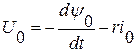
Эта система уравнений должна быть дополнена ещё уравнением движения или механического равновесия моментов на валу

,

.

Здесь М_внешн. – вращающийся момент турбины для генератора М_т или момент механизма М_мех для двигателя;

w_r – угловая скорость ротора;

— электромагнитный момент;

J – момент инерции вращающихся масс ротора, выраженный в кг×м 2

Преобразование переменных статора в системе координат А, В, С в новые переменные, связанные с системой координат d, q, 0 являясь формально математическим приёмом, имеет простое физическое объяснение.

При преобразовании переменных трёхфазная обмотка статора заменяется эквивалентной двухфазной, жёстко связанной с осями d и q ротора (вращается с той же скоростью, что и ротор со скоростью w_r ротора).

Дифференциальные уравнения равновесия дополним алгебраическими, связывающими потокосцепления и токи соответствующих контуров.

1) в продольной и поперечной осях машины, кроме потоков рассеяния существуют потоки в воздушном зазоре, пронизывающие все контуры, расположенные по соответствующим осям машины;

2) все параметры роторных контуров приведены к статору ( как – уточним позднее)

Тогда выражения для потокосцеплений статорных и роторных контуров, входящих в систему (2), имеют вид

,

,

, (4.2)

,

,

.

Так как преобразованные обмотки статора d и q неподвижны относительно ротора, то индуктивности и взаимные индуктивности этих обмоток, входящие в выражения (2), постоянны, если не учитывать изменения насыщения магнитной цепи. Таким образом, преобразование переменных (переход от системы координат А, В, С к осям d и q) позволяет избавиться от периодических коэффициентов в дифференциальных уравнениях (1) синхронной машины.

Уравнения (1) и (2) выражают основу теории обобщённой электрической машины.

При постоянной частоте вращения ротора (w_r = const) с учётом принятых допущений система уравнений (1) и (2) становится системой линейных дифференциальных уравнений, допускающей аналитическое решение, то есть можно получить аналитическое выражение для изменения тока статора во времени при коротком замыкании.

В системе (1) первые слагаемые первых двух уравнений для обмоток d и q статора представляют ЭДС трансформации, поскольку они вызываются изменением величин соответствующих потокосцеплений, а вторые слагаемые – ЭДС вращения. В установившемся режиме ЭДС трансформации отсутствуют.

В рассмотренной выше модели синхронной машины, соответствующей уравнениям Парка-Горева, ЭДС вращения представлены лишь частично, так как при синхронном вращении обмоток и магнитных потоков никаких ЭДС вращения в этих обмотках нет. Только при перемещении обмоток относительно вращающихся магнитных потоков, что в общем случае также имеет место при переходном процессе, в обмотках наводятся дополнительные ЭДС вращения (точнее ЭДС скольжения ― в обмотке d и в обмотке q, где w_r ¹ w_с), поток при работе СМ параллельно с системой неограниченной мощности всегда вращается с синхронной скоростью.

Источник

Преобразование парка

В случае вращающейся машины метка Park прикреплена к ротору. В тесте Парка токи синхронной машины обладают замечательным свойством быть непрерывным.

Резюме

Преобразование парка

и обратное преобразование (через обратную матрицу ):

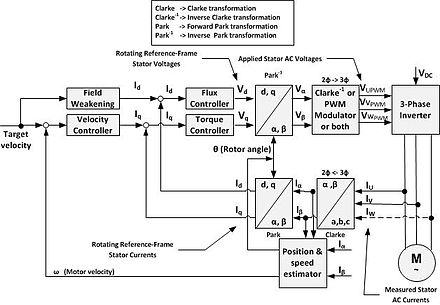
Dqo преобразование

Принцип

Преобразование dqo позволяет в сбалансированной трехфазной системе преобразовывать три переменные величины в две непрерывные величины. Это значительно упрощает решение уравнений. После расчета решения обратное преобразование используется для нахождения соответствующих трехфазных величин.

Преобразование Парка берет принципы преобразования Кларка, но продвигает его дальше. Рассмотрим систему трех уравновешенных трехфазных токов:

Геометрическая интерпретация

Таким образом, мы получаем новую ссылку:

Композиция этих двух вращений имеет для матрицы:

Эта матрица называется матрицей Кларка (хотя на самом деле это матрица Конкордии, похожая на матрицу Кларка, за исключением того, что она унитарна).

Матрица, полученная умножением матрицы Кларка на матрицу вращения, является матрицей преобразования dqo :

В случае синхронных машин преобразование dqo обладает замечательным свойством делать индуктивности постоянными во времени.

Заявление

Источник

Уравнения Парка-Горева. Система относительных единиц

Дальнейшие упрощения дифференциальных уравнений СГ связаны с приведением всех обмоток СГ к обмоткам статора и с введением относительных единиц для электрических и механических характеристик СГ в соответствии с выражениями

и т.д., (2.11)

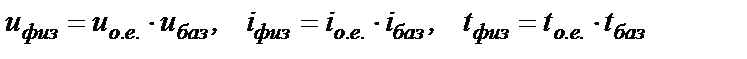
где индексом «баз» обозначены базисные величины.

За базисные величины принимаются амплитуды номинальных значений напряжения, тока, частота сетевого напряжения и т.д. Преимущество дифференциальных уравнений в относительных единицах в том, что упрощается выбор численного метода решения системы дифференциальных уравнений СГ, а также возможно сравнение между собой процессов в генераторах разных мощностей. Такая возможность сравнения является основой физического моделирования. С формальной точки зрения переход от физической системы уравнений (3.5) к уравнениям в относительных единицах представляет собой замену одних переменных другими.

Изложенные выше идеи простого описания СГ, а также учет уравнений движения ротора СГ под действием момента приводного двигателя (дизеля) и электромагнитного момента сопротивления генератора, приводят к системе уравнений Парка-Горева (сокращенно – УПГ) следующего вида:

(2.12)

— электромагнитный момент синхронного генератора, создающий сопротивление вращению;

— механическая постоянная времени агрегата «СГ + приводной двигатель», имеющих суммарный маховый момент GD 2 /4;

w_Б – базисная частота, равная частоте напряжения сети w_с;

р – число пар полюсов обмотки статора физического СГ;

S_Б – базисная мощность СГ, равная его номинальной полной мощности;

— потокосцепления обмоток модельного СГ, которые определяются выражениями

(2.13)

В выражениях (8)…(12) системы (2.13) индуктивные сопротивления определяются из рис.2.6, являющегося аналогом рис.2.5.

На рис.2.6 обозначены сопротивления:

x_ad – сопротивление взаимной индукции обмоток СГ по продольной оси d;

x_s – индуктивное сопротивление рассеяния обмоток статора;

x_sf – индуктивное сопротивление рассеяния обмотки возбуждения;

Полные индуктивные сопротивления обмоток равны сумме индуктивных сопротивлений взаимной индукции и индуктивного сопротивления рассеяния:

(2.14)

Время t в УПГ измеряется в электрических секундах, причем

1 секунда физическая = 314 секунд электрических (2.15)

Если в результате решения УПГ получены, например, токи i_d и i_q, то ток i_A фазы А физического генератора определится выражением

(2.16)

где w_с – частота тока в сети;

t – физическое время;

g₀ – начальный угол (при t=0) между осями d и a (см. рис.2.5).

Вращающий момент дизеля М_ДИЗ в системе (2.12) должен быть выражен в относительных единицах

(2.18)

Из системы (2.14) токи обмоток выражаются через потокосцепления по формулам

(2.19)

где

При моделировании процессов в СГ по УПГ (2.12) в качестве переменных интегрирования используются потокосцепления . Поэтому в (3.12) все токи должны быть заменены согласно (3.19). При решении УПГ будут получены значения потокосцеплений . Пересчет потокосцеплений в токи выполняется по формулам (2.19), а переход к физическим переменным осуществляется по формулам типа (2.17).

Вопросы для самоконтроля

1. Приведите уравнения Парка-Горева.

2. Приведите выражения потокосцеплений обмоток СГ.

2. Приведите развернутую схему обмоток СГ в осях его ротора.

3. Приведите выражения величин модели СГ в относительных единицах.

4. Как рассчитать токи физических обмоток статора через токи статора, определенные в осях d и q?

Источник