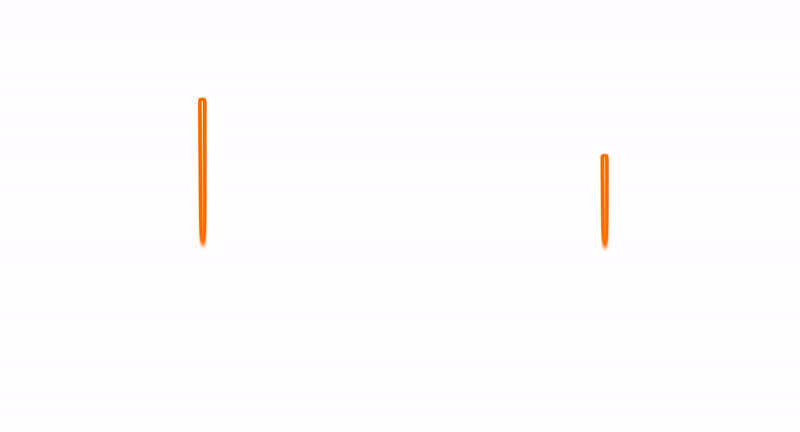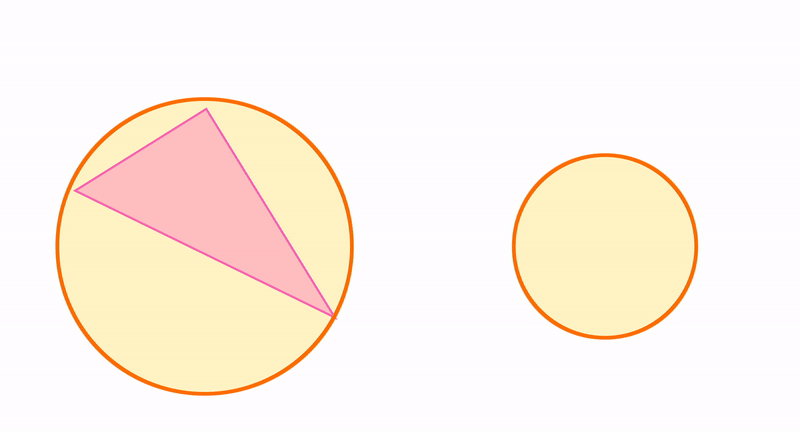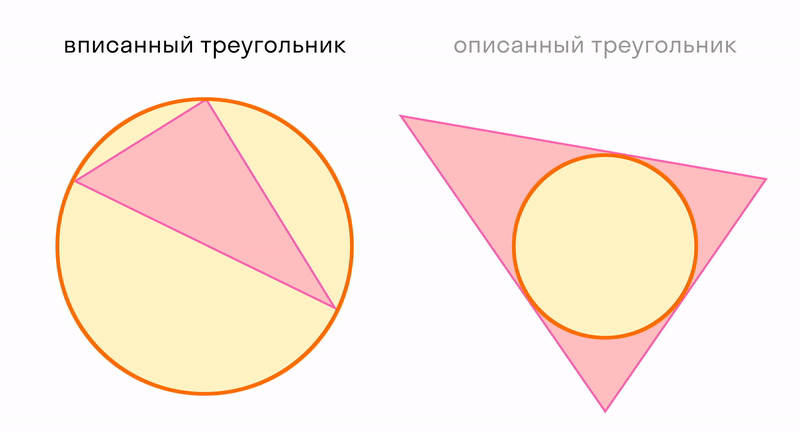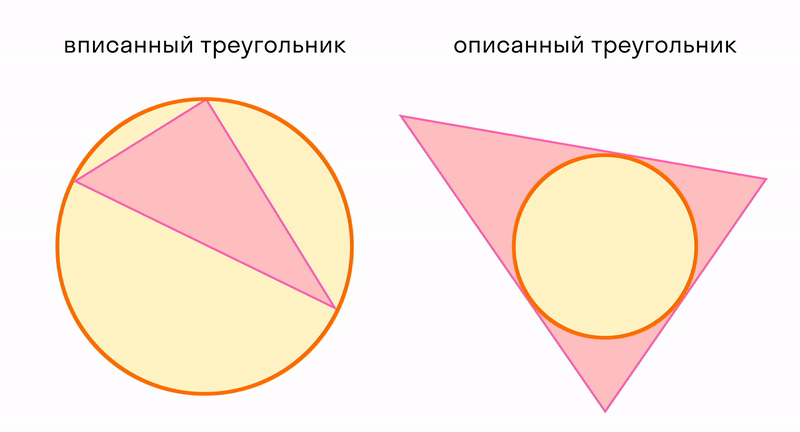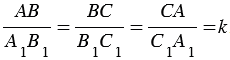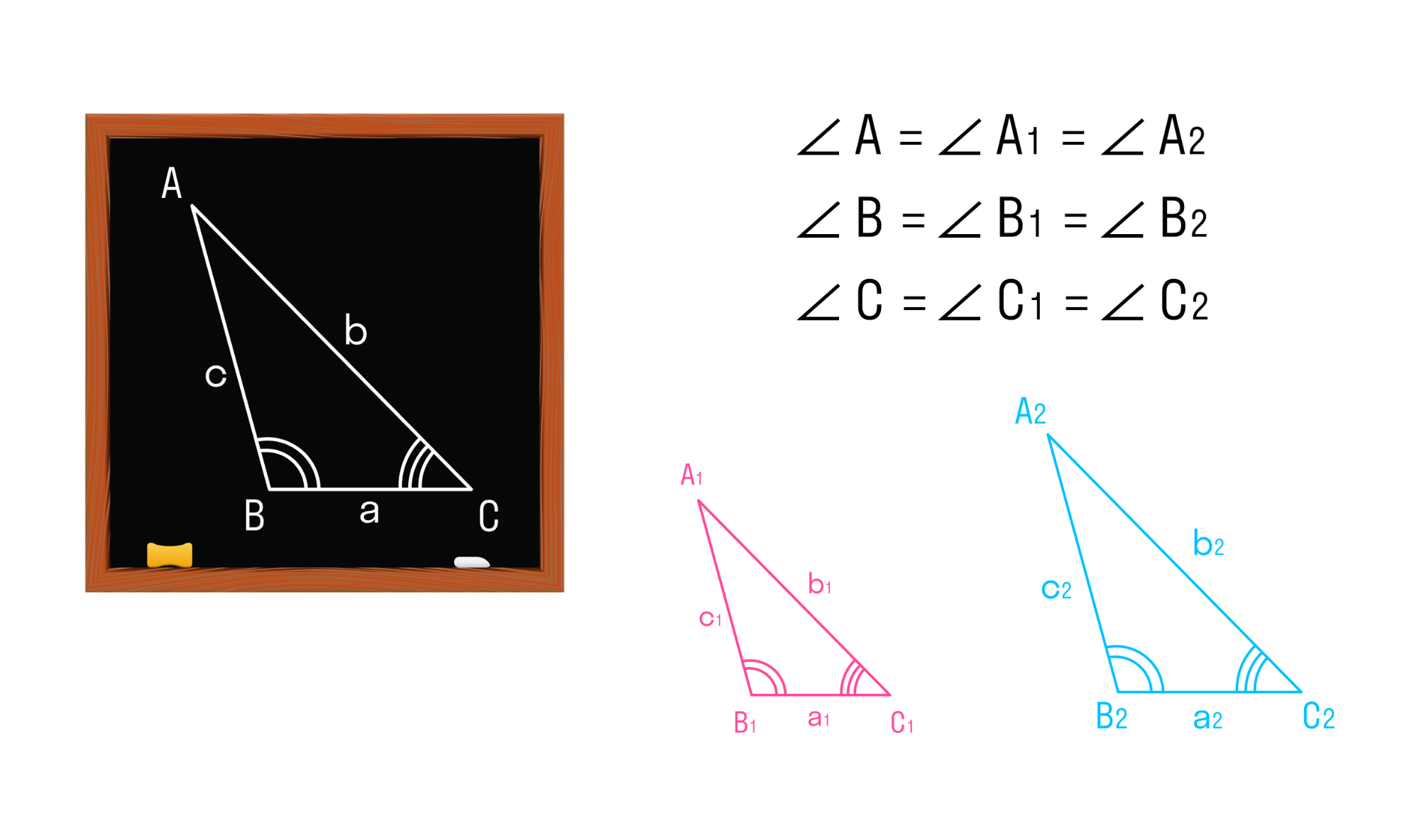Что такое правильная фигура
Правильные фигуры в геометрии
Описание презентации по отдельным слайдам:
Описание слайда:
Правильные фигуры
в геометрии
Учитель математики Беленкова Ольга Александровна
Описание слайда:
Правильные многоугольники
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
Описание слайда:
Свойства правильного многоугольника:
Правильный многоугольник является вписанным в окружность и описанным около окружности.
Центр правильного многоугольника совпадает с центрами вписанной и описанной окружностей.
Периметры правильных n-угольников относятся как радиусы описанных окружностей.
Описание слайда:
Виды правильных многоугольников.
Описание слайда:
Правильные многогранники
«Правильных многогранников вызывающе мало, – написал когда-то Л. Кэрролл – но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук».
Описание слайда:
Многогранник- это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности.
Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками.
Стороны граней называются рёбрами многогранника, а вершины – вершинами многогранника.
Описание слайда:
Существует 5 видов правильных многогранников:
1)тетраэдр
2) гексаэдр
3) додекаэдр
4)октаэдр
5)икосаэдр
Описание слайда:
Тетраэдр
Свойства:
Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Теорема. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.
Описание слайда:
Гексаэдр
Свойства :
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным.
В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
Описание слайда:
Додекаэдр
(от греческого dodeka – двенадцать и hedra – грань) Правильный многогранник, составленный из 12 равносторонних пятиугольников. Додекаэдр имеет 20 вершин и 30 ребер. Вершина додекаэдра является вершиной трех пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324°.
Описание слайда:
Описание слайда:
Икосаэдр
Свойства:
Икосаэдр можно вписать в куб, при этом, шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.
Описание слайда:
Спасибо за внимание!
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Правильные многогранники. Часть 1. Трёхмерие
Введение. Постановка вопроса.
В школьной программе, к сожалению, сферическую геометрию и геометрию Лобачевского не изучают. Тем временем, их изучение совместно с Евклидовой геометрией, позволяет глубже понять происходящее с объектами. Например, понять связь правильных многогранников с разбиениями сферы, разбиениями плоскости Евклида и разбиениями плоскости Лобачевского.
Знания геометрии пространств постоянной кривизны помогает подниматься над трёхмерием и выявлять многогранники в пространствах размерности 4 и выше. Вопросы нахождения многогранников, нахождения разбиений пространств постоянной кривизны, вывода формулы двугранного угла правильного многогранника в n-мерном пространстве — так тесно переплетены, что выносить всё это в название статьи оказалось проблематично. Пусть в центре внимания будут, всем понятные, правильные многогранники, хотя они не только результат всех выводов, но и, одновременно, инструмент для постижения пространств высших размерностей и равномерно искривлённых пространств.
Для тех кто не знает (забыл) сообщаю (напоминаю), что в привычном нам трёхмерном Евклидовом пространстве всего пять правильных многогранников:
| 1. Тетраэдр: | 2. Куб: | 3. Октаэдр: | 4. Додекаэдр: | 5. Икосаэдр: |
 |  |  |  |  |
В трёхмерном пространстве правильным многогранником называется выпуклый многогранник, у которого все вершины равны между собой, все рёбра равны между собой, все грани равны между собой и грани являются правильными многоугольниками.
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.
Вершины равны между собой означает, что количество рёбер и количество граней подходящих к каждой вершине одинаковое и подходят они под одинаковыми углами, в каждой вершине.
Оказывается, правильные многогранники удобно обозначать их символом Шлефли
В такой записи наши многогранники получат обозначения:
1. Тетраэдр <3, 3>,
2. Куб <4, 3>,
3. Октаэдр <3, 4>,
4. Додекаэдр <5, 3>,
5. Икосаэдр <3, 5>
Например, <4, 3>— куб имеет 4 угольные грани, в каждой вершине сходится по 3 таких грани.
У октаэдра <3, 4>наоборот, грани 3 угольные, сходятся по 4 штуки в вершине.
Таким образом символ Шлефли полностью определяет комбинаторное строение многогранника.
Почему правильных многогранников всего 5? Может быть их больше?
Чтобы сполна дать ответ на этот вопрос, нужно сначала получить интуитивное представление о геометрии на сфере и на плоскости Лобачевского. Тем у кого такого представления ещё нет постараюсь дать необходимые объяснения.
Сфера
1. Что такое точка на сфере? Думаю, что всем интуитивно понятно. Мысленно не сложно представить точку на сфере.
2. Что такое отрезок на сфере? Берём две точки и соединяем их кратчайшим расстоянием на сфере, получится дуга, если смотреть на сферу со стороны.
3. Если продолжить этот отрезок в обе стороны, то он замкнётся и получится окружность. При этом плоскость окружности содержит центр сферы, это следует из того, что две исходные точки мы соединили кратчайшим, а не произвольным, расстоянием. Это со стороны она выглядит, как окружность, а в терминах сферической геометрии это прямая, так как была получена из отрезка, продолжением до бесконечности в обе стороны.
4. И, наконец, что такое треугольник на сфере? Берём три точки на сфере и соединяем их отрезками.
По аналогии с треугольником можно нарисовать произвольный многоугольник на сфере. Для нас принципиально важно свойство сферического треугольника, заключающееся в том, что сумма углов у такого треугольника больше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных сферических треугольников различна. Чем больше треугольник, тем БОЛЬШЕ у него сумма углов.
Соответственно, появляется 4-й признак равенства треугольников на сфере — по трём углам: два сферических треугольника равны между собой, если у них соответствующие углы равны.
Для простоты саму сферу проще не рисовать, тогда треугольник будет выглядеть немного раздутым:
Сферу ещё называют пространством постоянной положительной кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.
Лобачевский
Теперь, когда мы познакомились с геометрией на сфере, понять геометрию на гиперболической плоскости, открытую великим русским учёным Николаем Ивановичем Лобачевским, будет тоже не сложно, так как тут всё происходит аналогично сфере, только «наизнанку», «наоборот». Если дуги на сфере мы проводили окружностями, с центром внутри сферы, то теперь дуги надо проводить окружностями с центром за пределами сферы.
Приступим. Плоскость Лобачевского будем представлять в интерпретации Пуанкаре II (Жюль Анри́ Пуанкаре́, великий французский учёный), эту интерпретацию геометрии Лобачевского ещё называют диском Пуанкаре.
1. Точка в плоскости Лобачевского. Точка — она и в Африке точка.
2. Отрезок на плоскости Лобачевского. Соединяем две точки линией по кратчайшему расстоянию в смысле плоскости Лобачевского.
Кратчайшее расстояние строится следующим образом:
Надо провести окружность ортогональную диску Пуанкаре, через заданные две точки (Z и V на рисунке). Центр этой окружности будет находиться всегда за пределами диска. Дуга соединяющая исходные две точки будет кратчайшим расстоянием в смысле плоскости Лобачевского.
3. Убрав вспомогательные дуги, получим прямую E1 — H1 в плоскости Лобачевского.
Точки E1, H1 «лежат» на бесконечности плоскости Лобачевского, вообще край диска Пуанкаре — это всё бесконечно удалённые точки плоскости Лобачевского.
4. И наконец, что такое треугольник в плоскости Лобачевского? Берём три точки и соединяем их отрезками.
По аналогии с треугольником, можно нарисовать произвольный многоугольник на плоскости Лобачевского. Для нас принципиально важно свойство гиперболического треугольника, заключающееся в том, что сумма углов у такого треугольника всегда меньше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных гиперболических треугольников различна. Чем больше треугольник по площади, тем МЕНЬШЕ у него сумма углов.
Соответственно, тут тоже имеет место 4-й признак равенства гиперболических треугольников — по трём углам: два гиперболических треугольника равны между собой, если у них соответствующие углы равны.
Для простоты сам диск Пуанкаре иногда можно не рисовать, тогда треугольник будет выглядеть немного «усохшим», «сдутым»:
Плоскость Лобачевского (и вообще пространство Лобачевского любой размерности) ещё называют пространством постоянной ОТРИЦАТЕЛЬНОЙ кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.
Правильные разбиения двумерной Сферы и правильные трёхмерные многогранники
Всё сказанное про сферу и плоскость Лобачевского относится к двумерию, т.е. поверхность сферы — двумерна. Какое это имеет отношению к трёхмерию, указанному в заголовке статьи? Оказывается, каждому трёхмерному правильному Евклидову многограннику взаимно однозначно соответствует своё разбиение двумерной сферы. Лучше всего это видно на рисунке:
Чтобы из правильного многогранника получить разбиение сферы, нужно описать вокруг многогранника сферу. Вершины многогранника окажутся на поверхности сферы, соединив эти точки отрезками на сфере (дугами), получим разбиение двумерной сферы на правильные сферические многоугольники. Для примера сделана видео демонстрация как икосаэдр соответствует разбиению сферы на сферические треугольники и обратно, как разбиение сферы на сферические треугольники, сходящиеся по пять штук в вершине, соответствует икосаэдру.
Чтобы по разбиению сферы построить многогранник, соответствующие дугам вершины разбиения нужно соединить обычными, прямолинейными, Евклидовыми отрезками.
Соответственно символ Шлефли икосаэдра <3, 5>— трёхугольники, сходящиеся по пять штук в вершине, задаёт не только структуру этого многогранника, но и структуру разбиения двумерной сферы. Аналогично и с другими многогранниками, их символы Шлефли задают и структуру соответствующих разбиений. Более того, разбиения плоскости Евклида и плоскости Лобачевского на правильные многоугольники, тоже можно задавать символом Шлефли. Например, <4, 4>— четырёхугольники, сходящиеся по четыре — это всем привычная нам тетрадь в клеточку, т.е. это разбиение плоскости Евклида на квадраты. А есть ли другие разбиения плоскости Евклида? Увидим дальше.
Построение разбиений двумерной сферы, плоскости Евклида и плоскости Лобачевского
Для построения разбиений двумерных пространств постоянной кривизны (таково общее название этих трёх пространств) нам потребуется элементарная школьная геометрия и знание того, что сумма углов сферического треугольника больше 180 градусов (больше Пи), что сумма углов гиперболического треугольника меньше 180 градусов (меньше Пи) и что такое символ Шлефли. Обо всём об этом уже сказано выше.
Итак, возьмём произвольный символ Шлефли
Рассмотрим правильный p1 угольник, проведём отрезки, соединяющие его центр и вершины. Получим p1 штук равнобедренных треугольника (на рисунке показан только один такой треугольник). Сумму углов каждого из этих треугольников обозначим за t и выразим t через пи и коэффициент лямда.
Тогда если лямда = 1, то треугольник Евклидов, т.е. находится в Евклидовой плоскости, если лямда в интервале (1, 3), то это значит, что сумма углов больше пи и значит этот треугольник сферический (не трудно представить, что при увеличении сферического треугольника в пределе получается окружность с тремя точками на ней, в каждой точке угол треугольника получается равным пи, а в сумме 3*пи. Это объясняет верхнюю границу интервала = 3). Если же лямда в интервале (0, 1), то треугольник гиперболический, так как сумма углов у него меньше пи (т.е. меньше 180 градусов). Коротко это можно записать так:
Не трудно посчитать, что:
С другой стороны, для сходимости в вершине p2 штук (т.е. целого числа) таких же многоугольников нужно, чтобы
Приравнивая выражения для 2*бетта, найденные из условия сходимости и из многоугольника:
Получили уравнение которое показывает какое из трёх пространств разбивает фигура заданная своим символом Шлефли
Решение этого уравнения заключается в переборе всех возможных значений для p1, p2 больших либо равных 3 и вычислении значения лямда. Если оно получится равным 1, то
Откуда видно, что:
1. Сфере соответствует всего 5 решений, когда лямда больше 1 и меньше 3, они выделены зелёным цветом в таблице. Это: <3, 3>— тетраэдр, <3, 4>— октаэдр, <3, 5>— икосаэдр, <4, 3>— куб, <5, 3>— додекаэдр. Их картинки были представлены в начале статьи.
2. Разбиениям Евклидовой плоскости соответствует всего три решения, когда лямда = 1, они выделены синим цветом в таблице. Вот как выглядят эти разбиения.


3. И наконец, все остальные комбинации
Основы геометрии
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
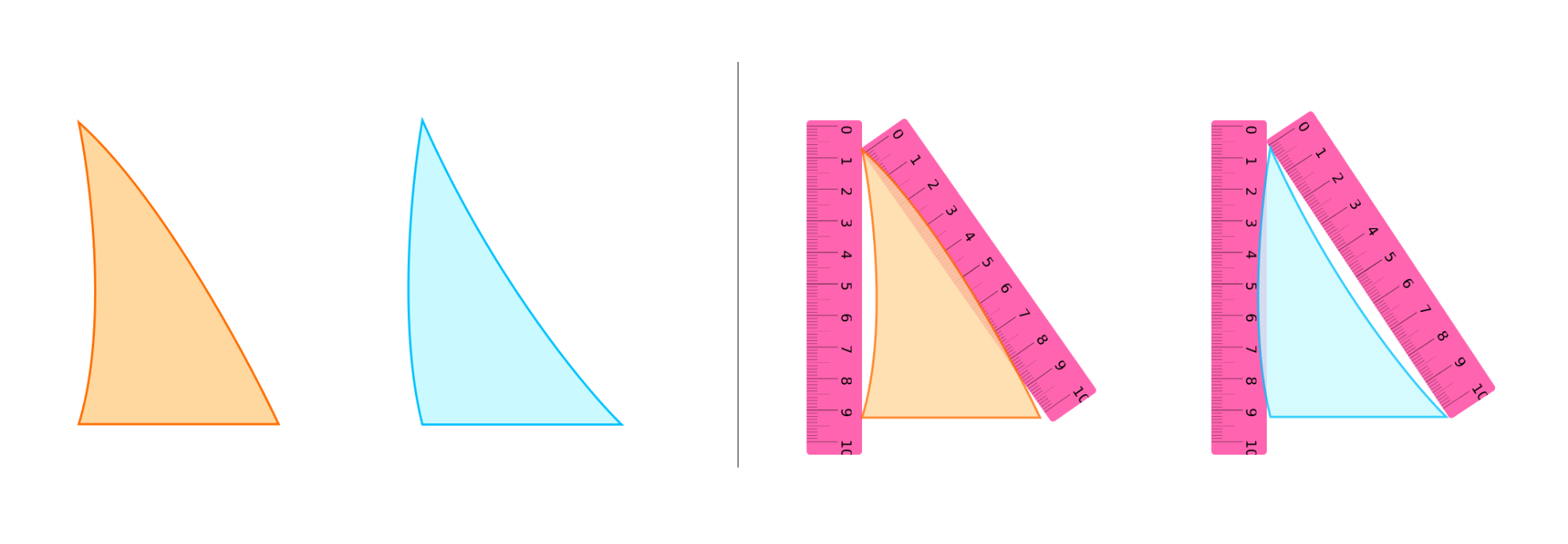
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
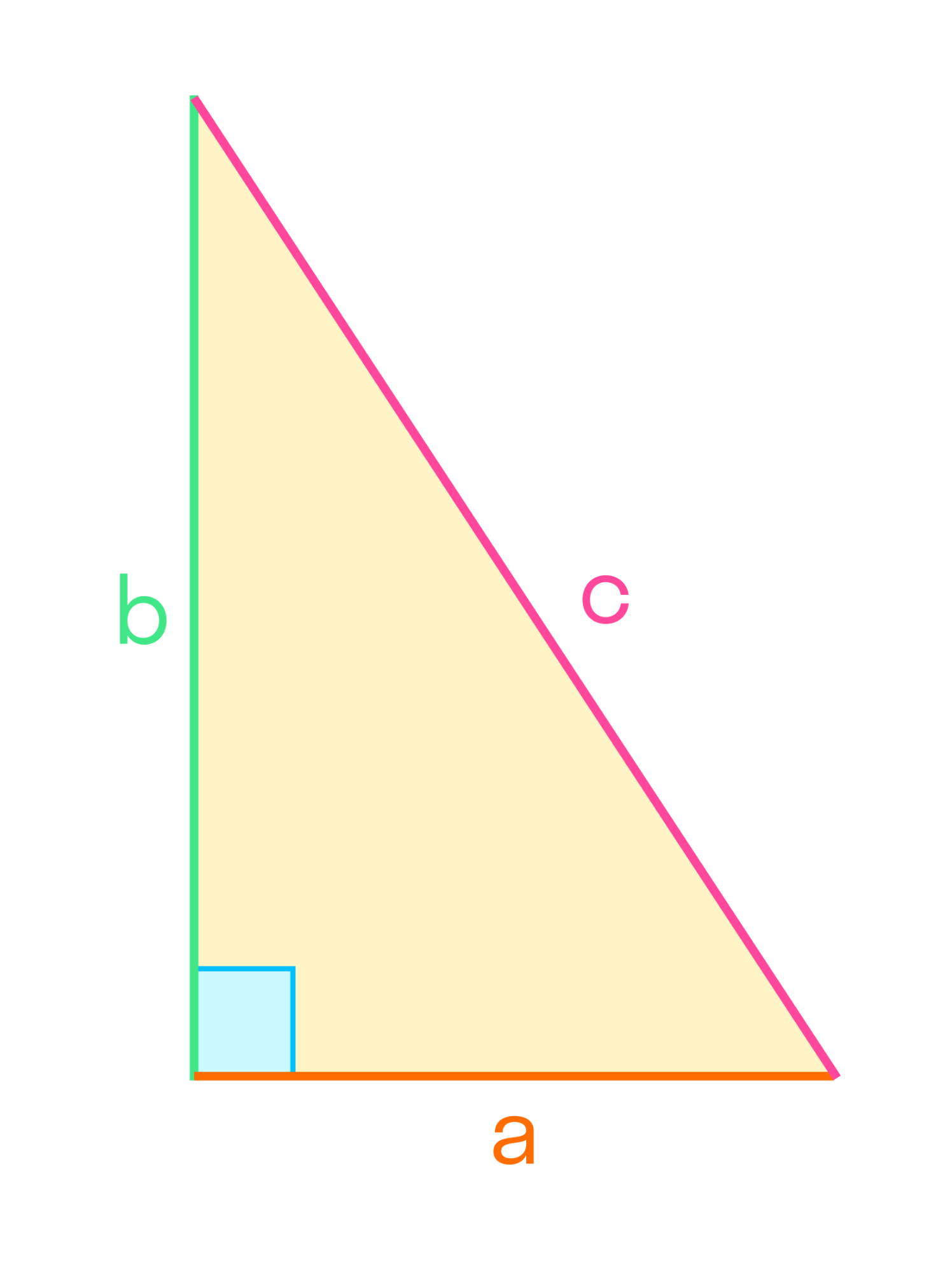
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
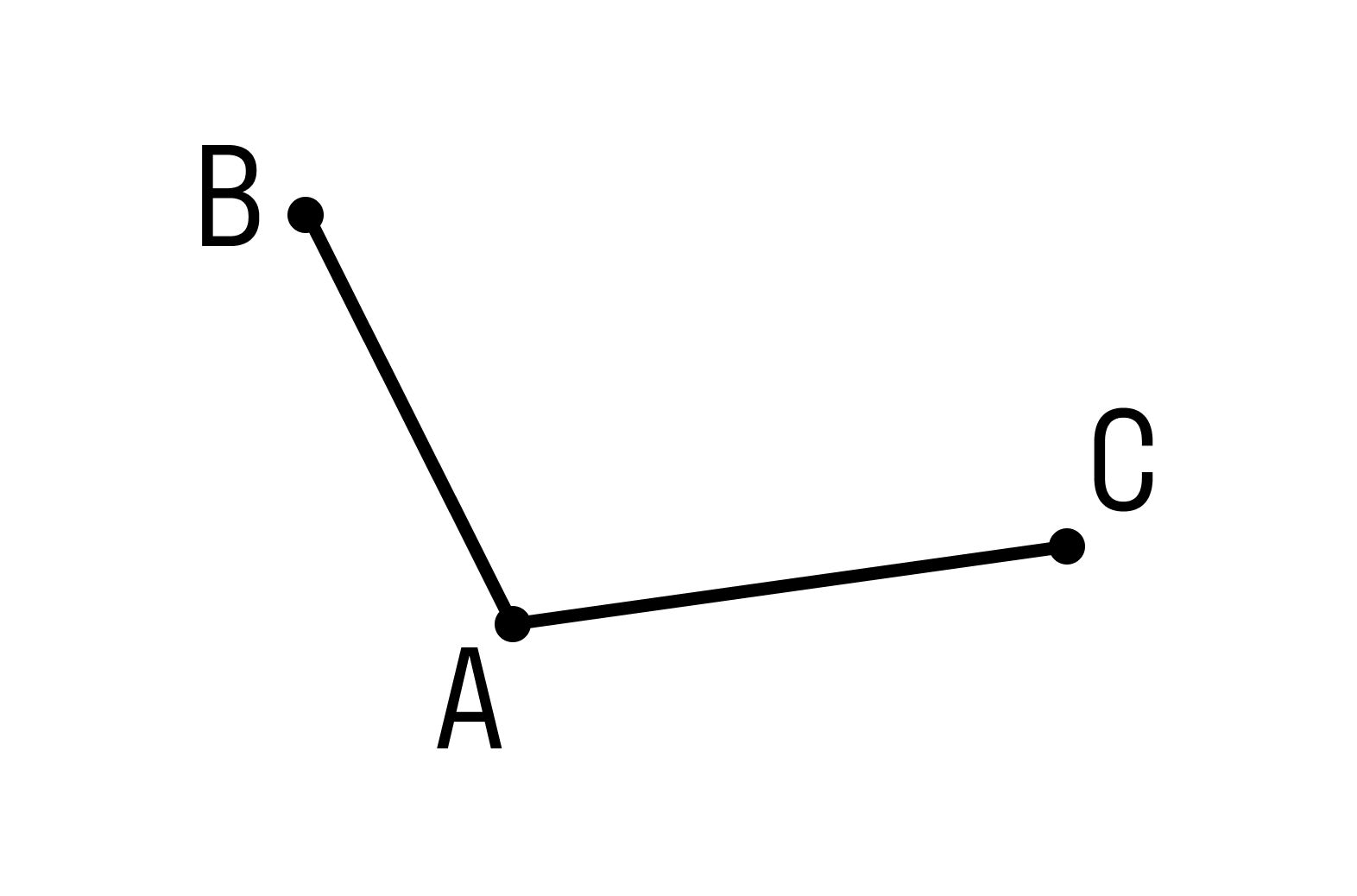
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
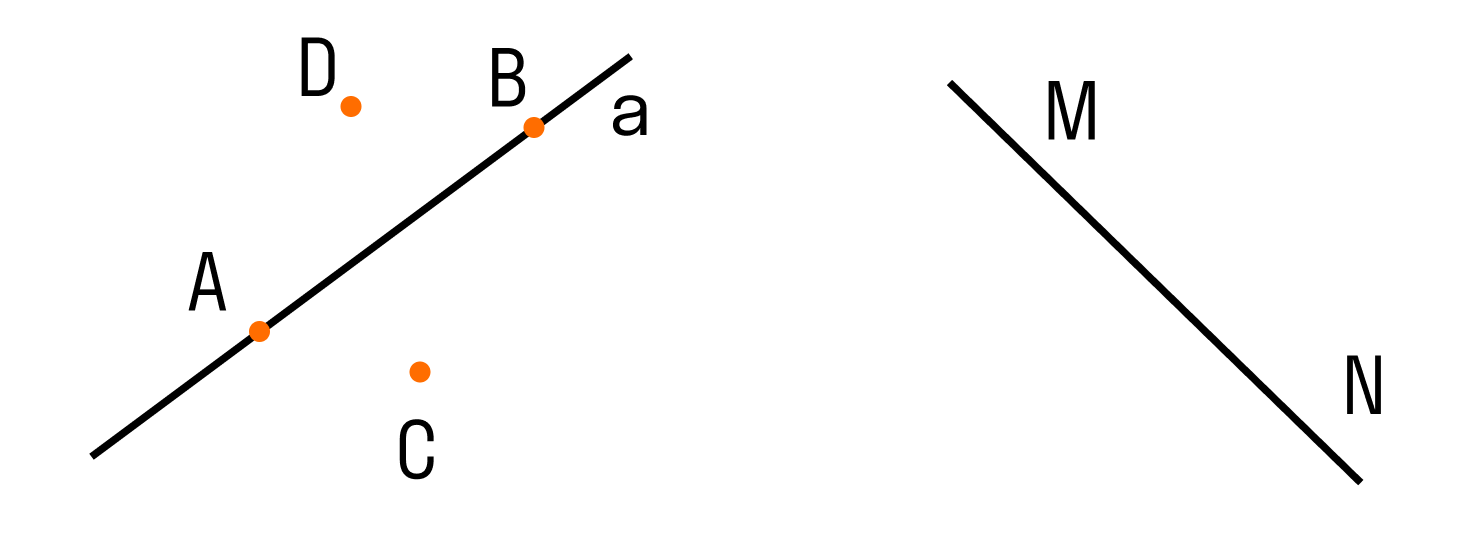
Два варианта расположения точек относительно прямой:
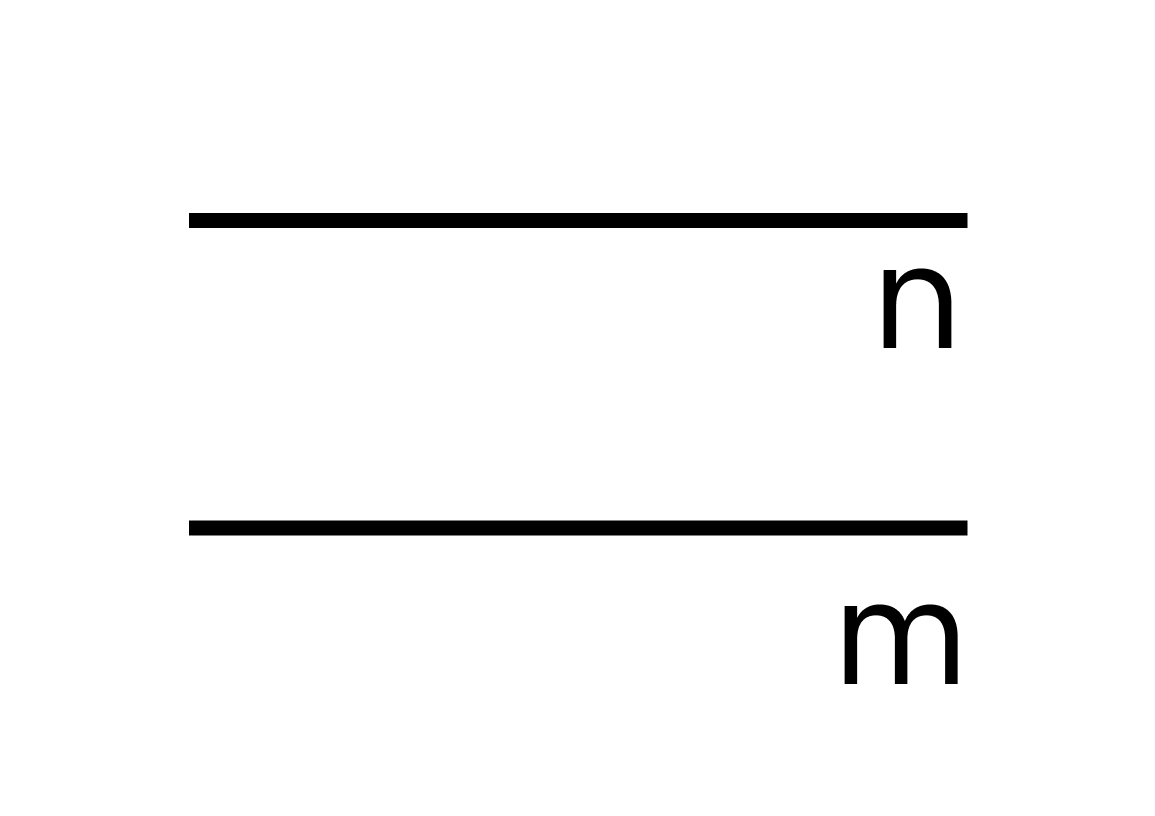
Если рассмотреть две прямые, то возможны два варианта их расположения:
Для записи не пересекающихся прямых используют специальный знак — 
то есть m 
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
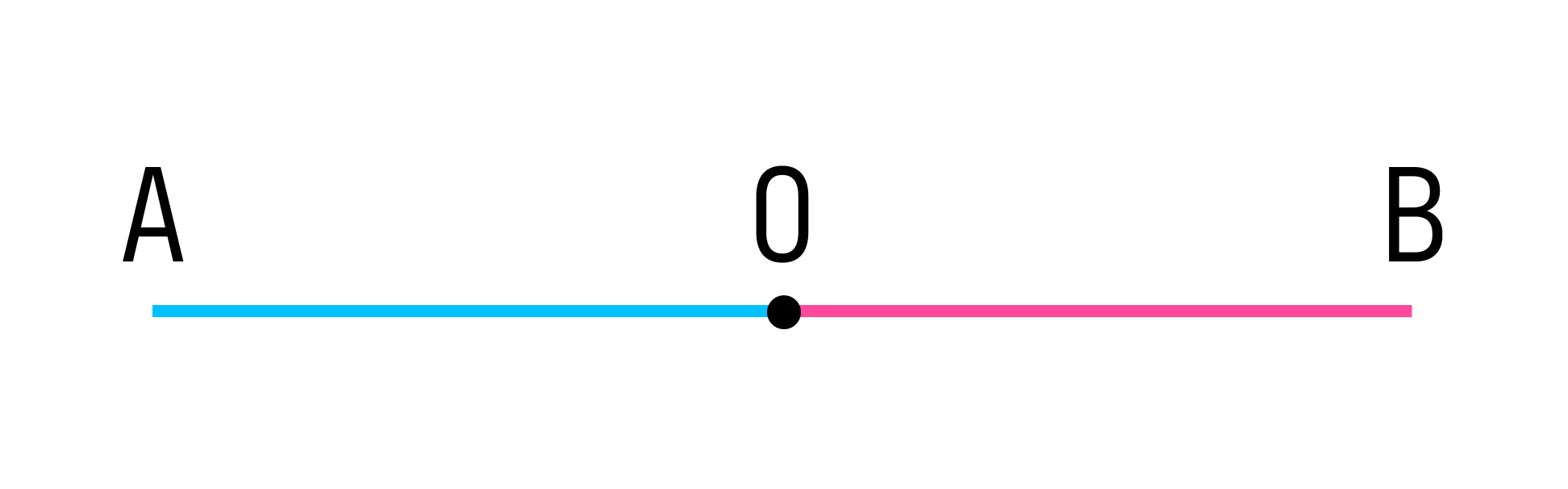
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
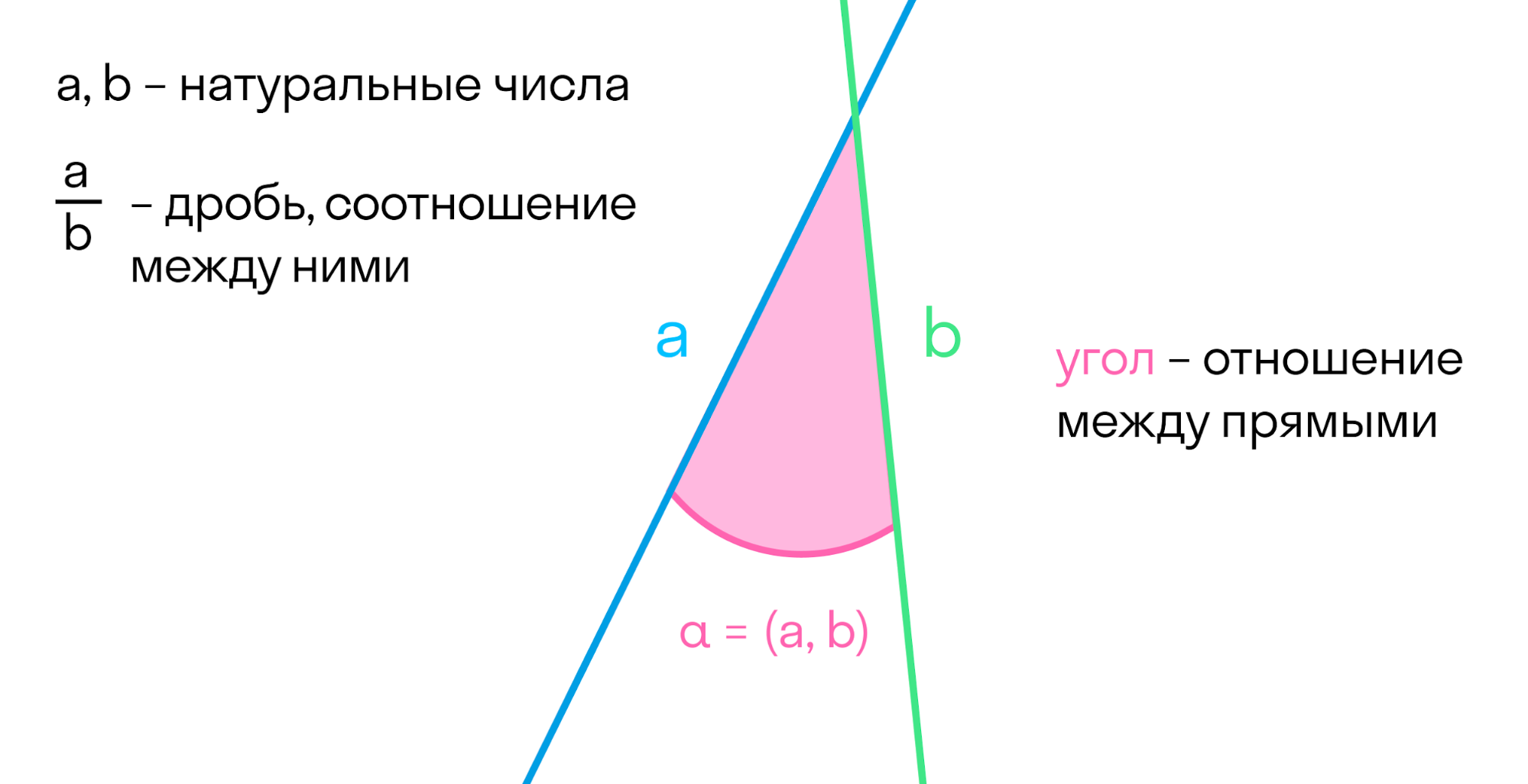
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
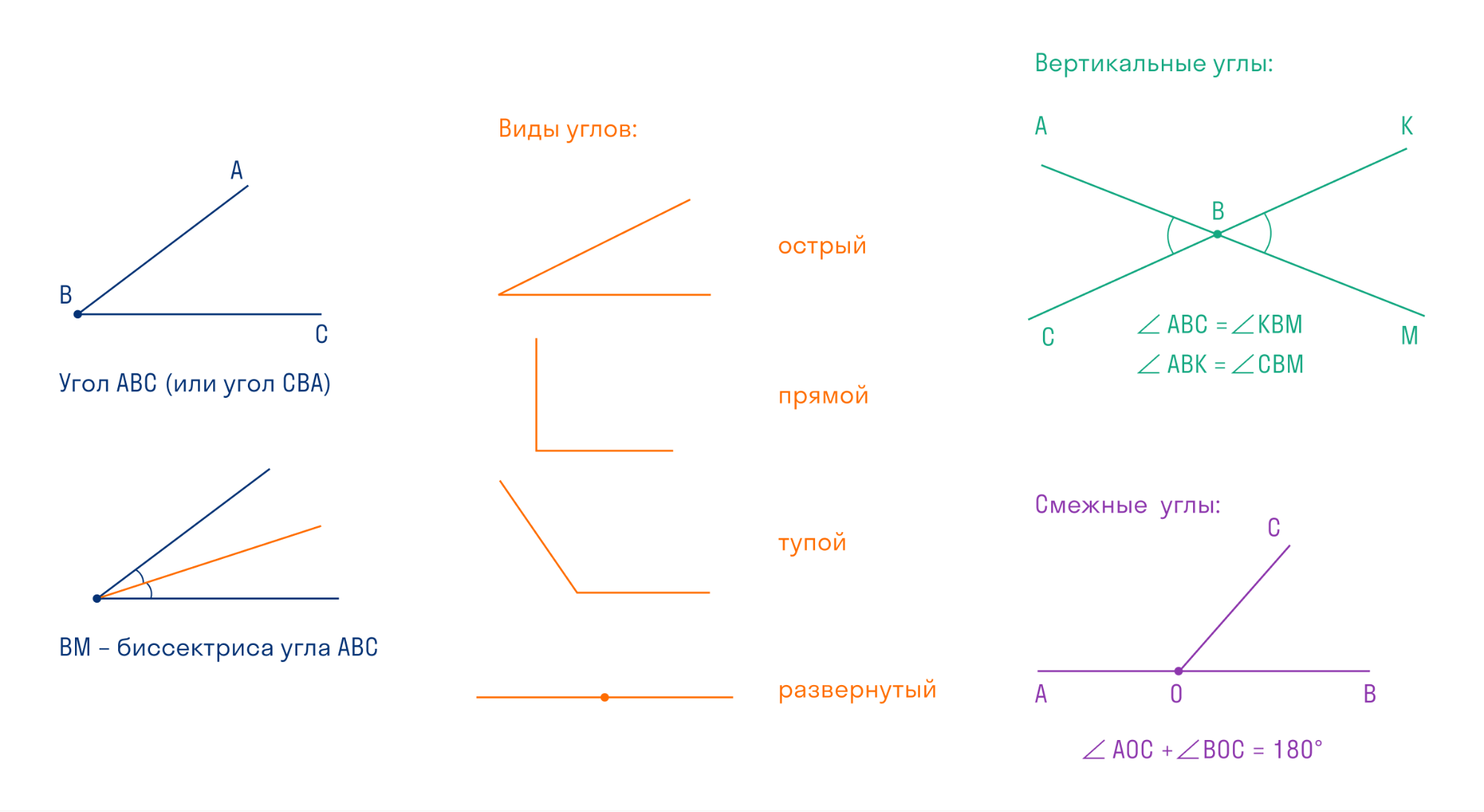
Есть разные виды углов, выделим самые часто встречающиеся:
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
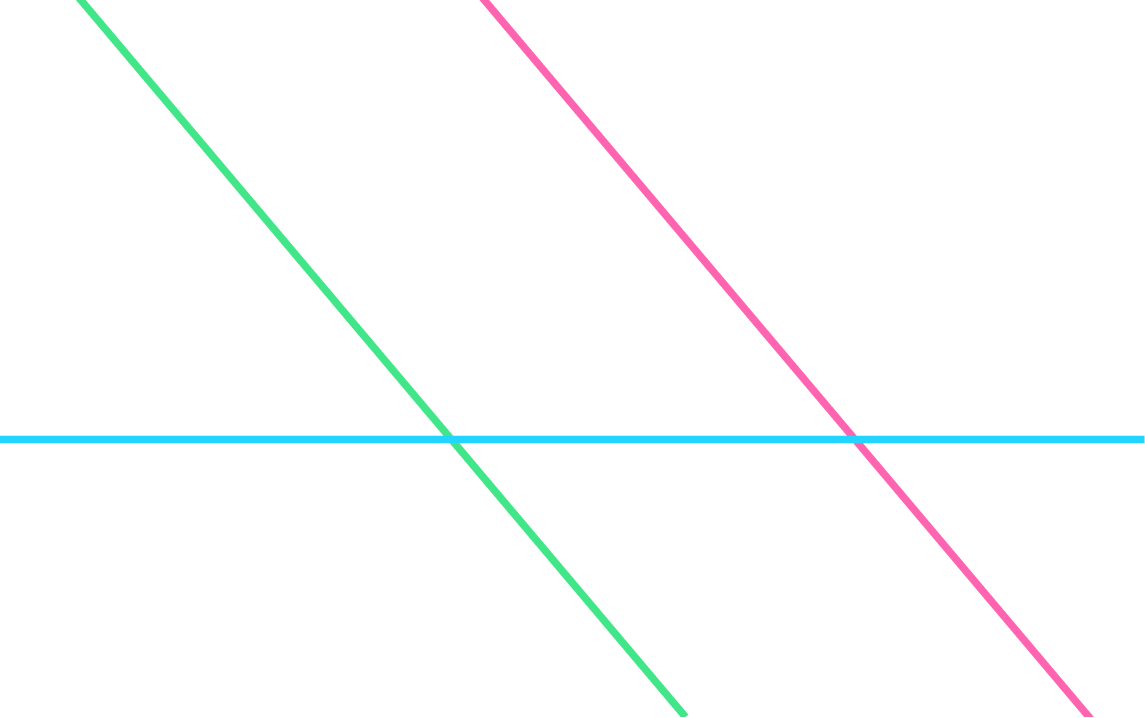
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
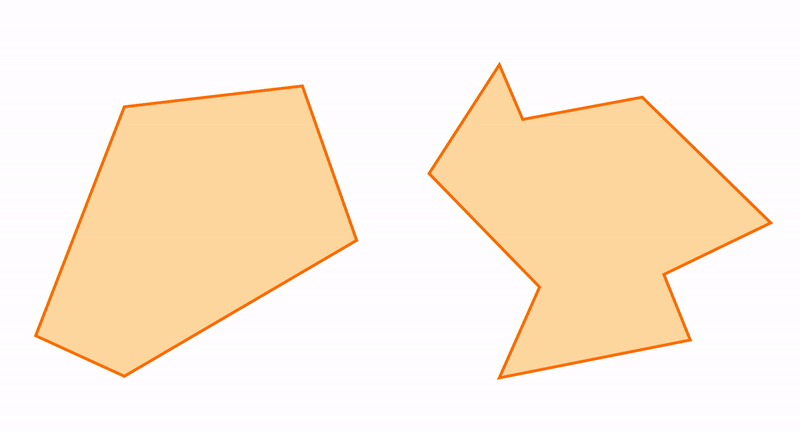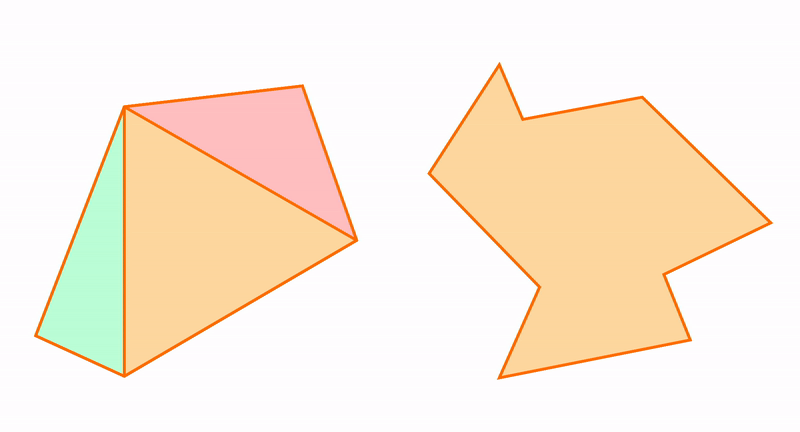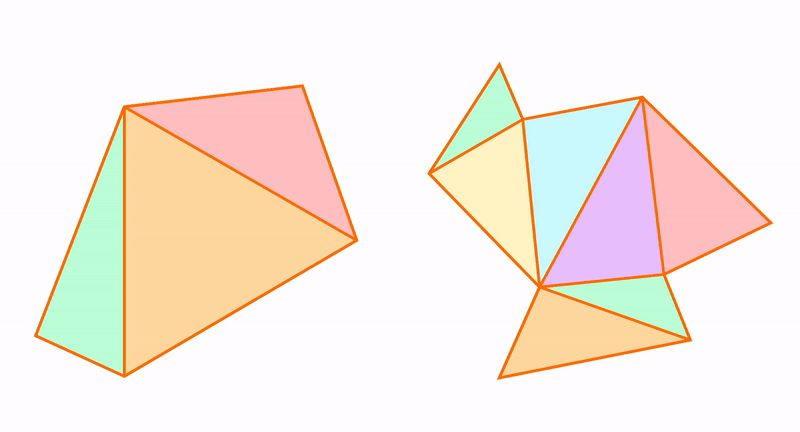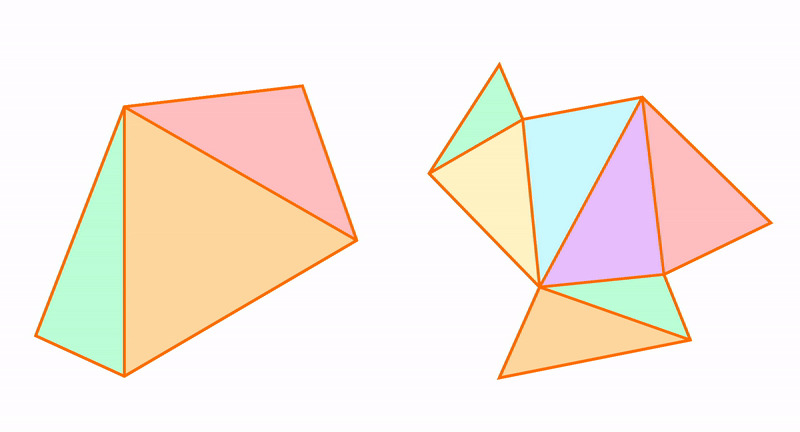
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Сумма любых двух сторон треугольника больше его третьей стороны.
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
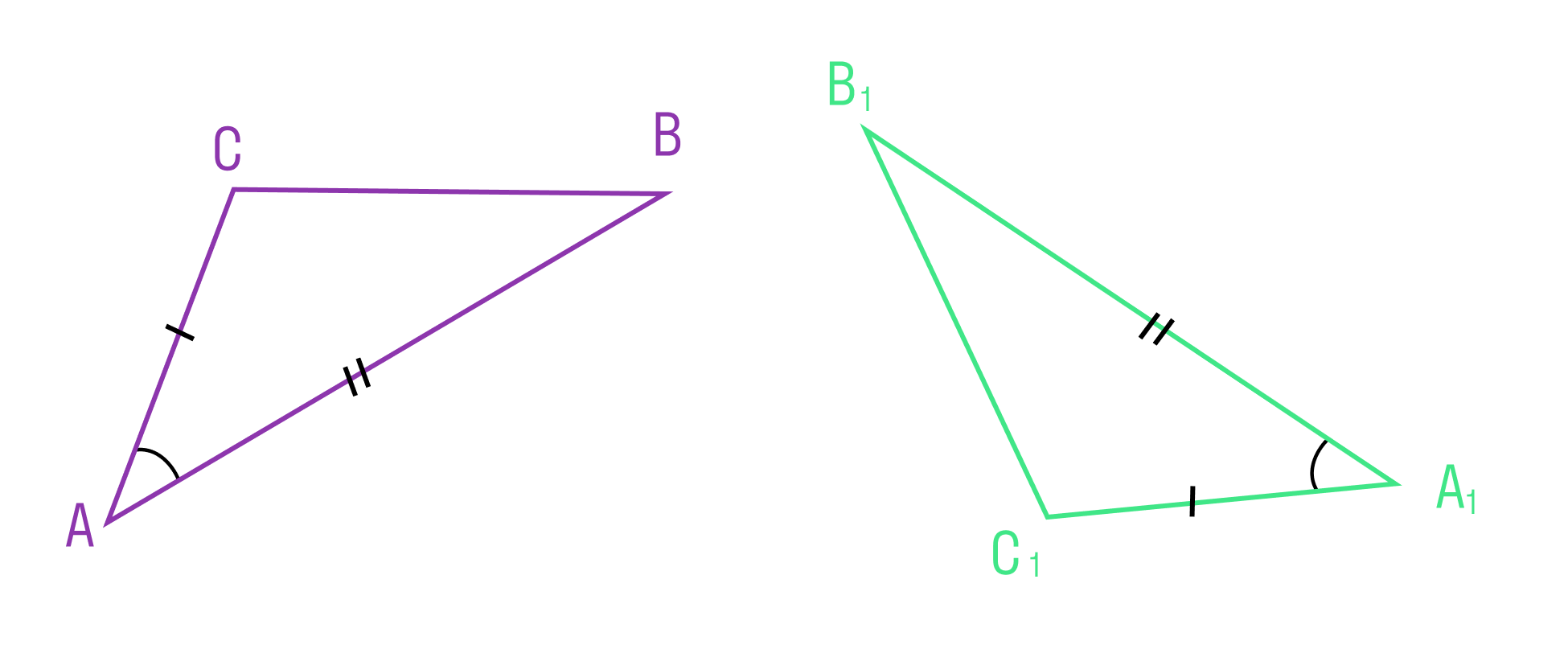
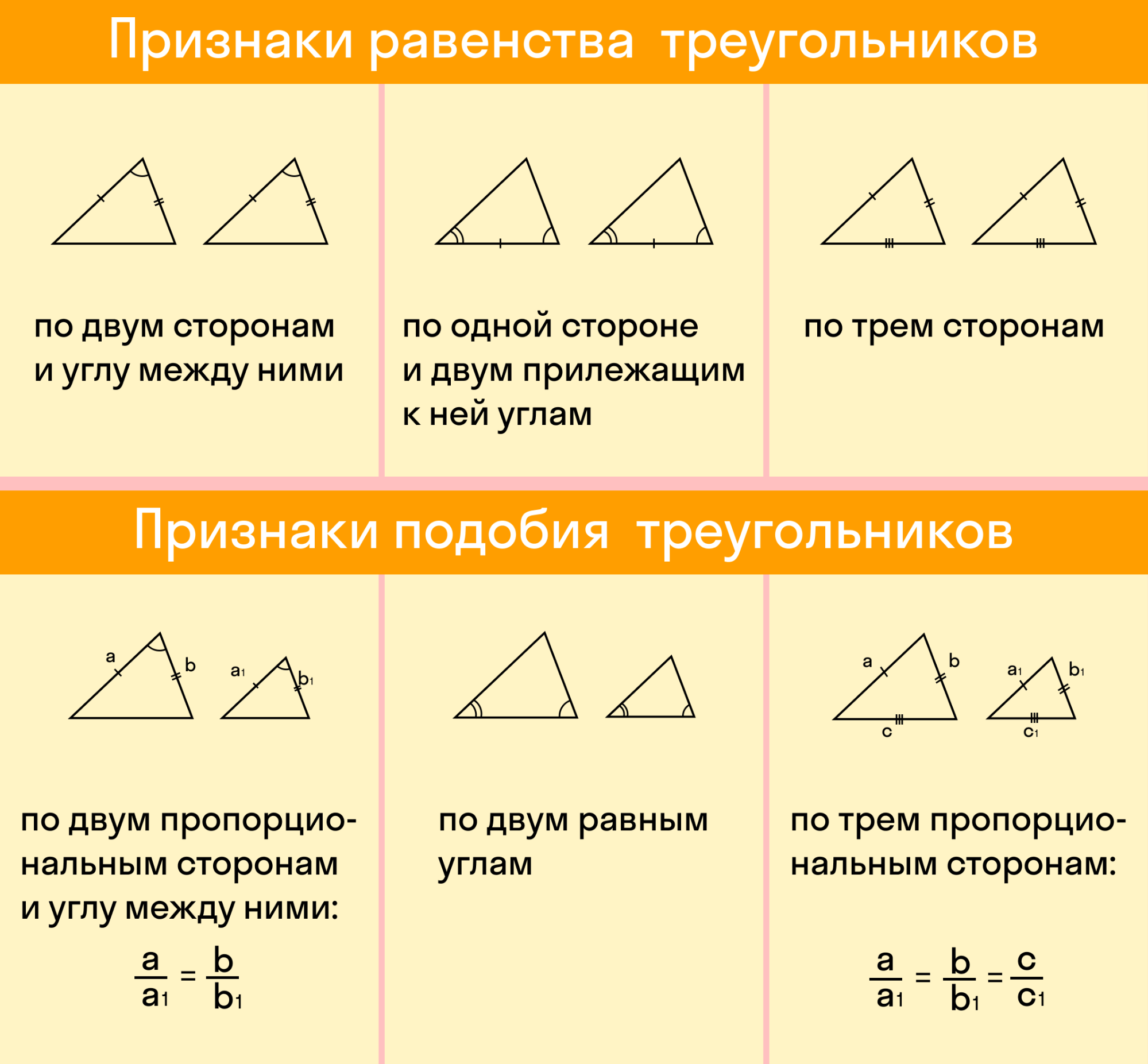
Первый признак равенства треугольников звучит так:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
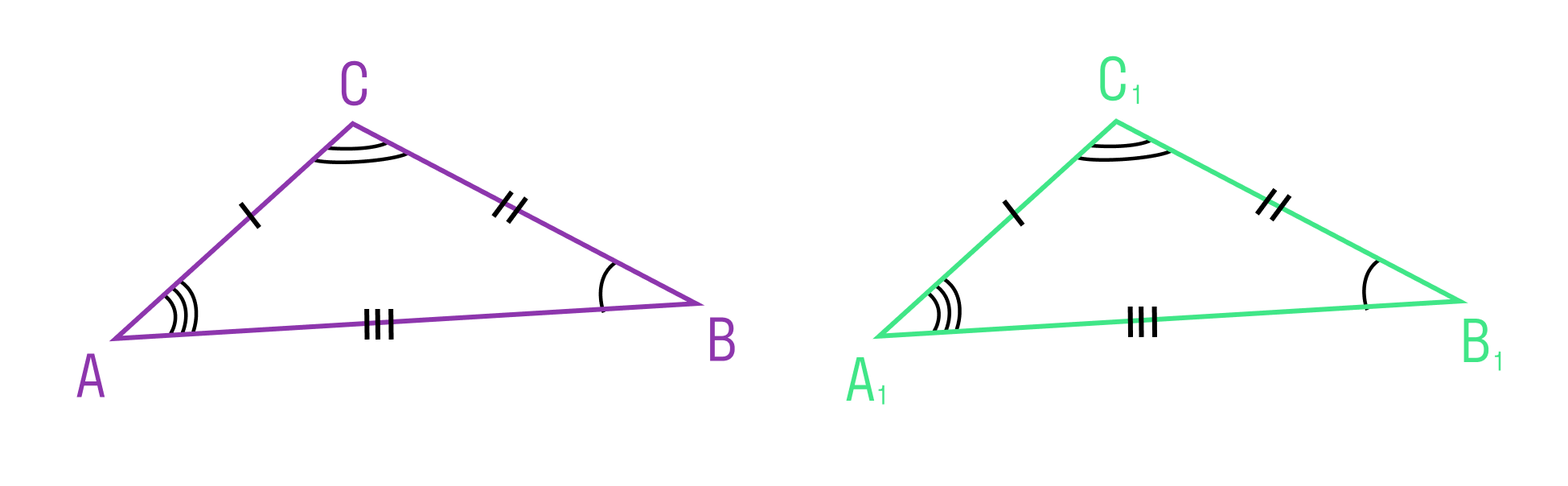
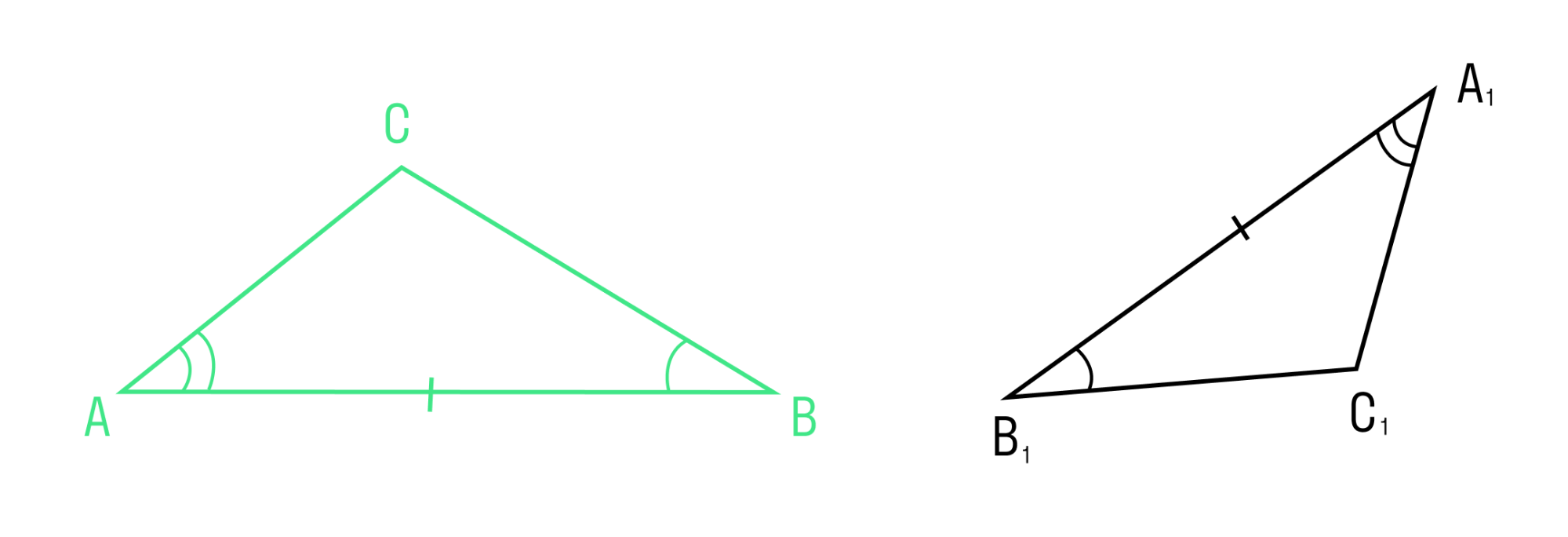
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
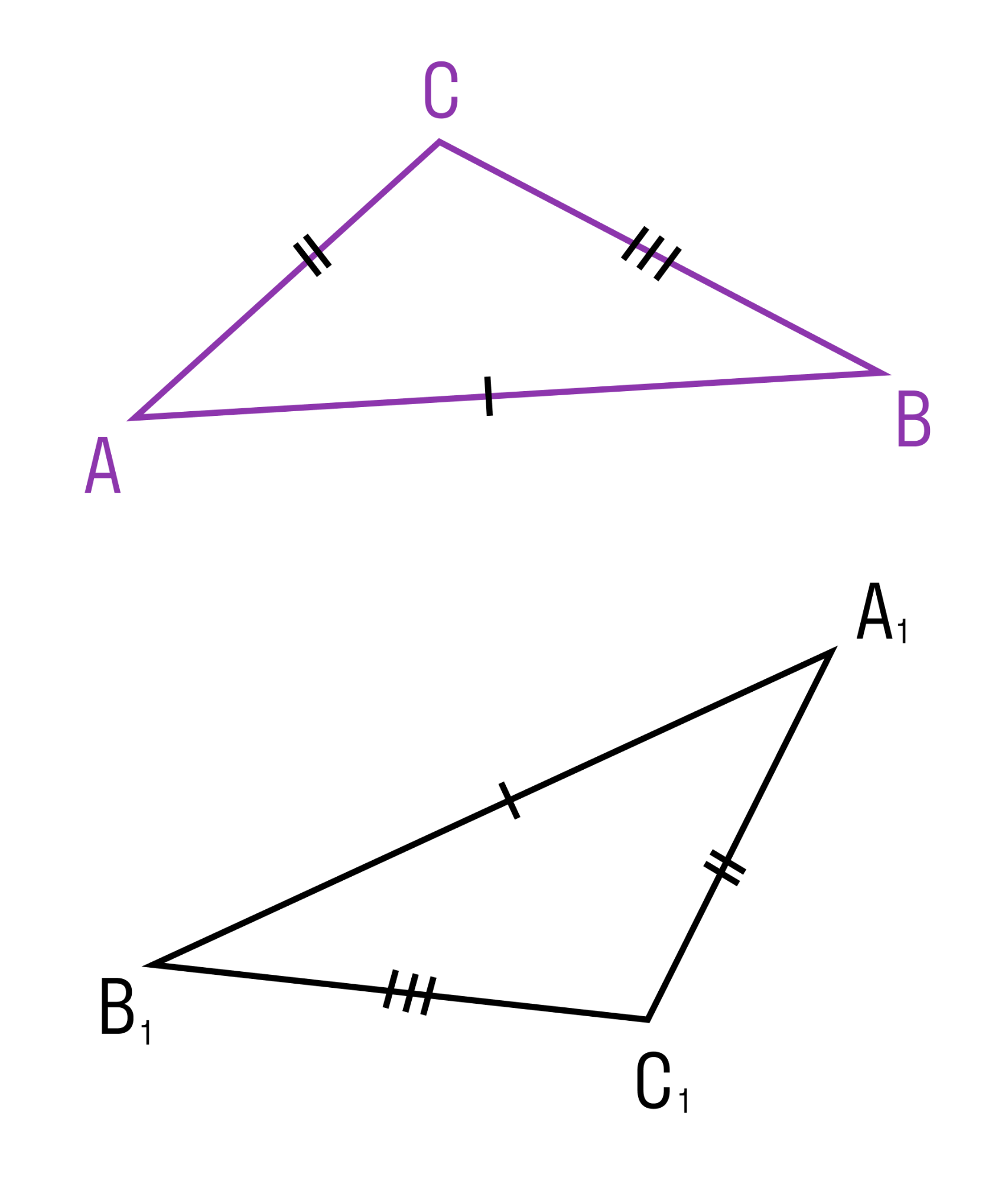
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
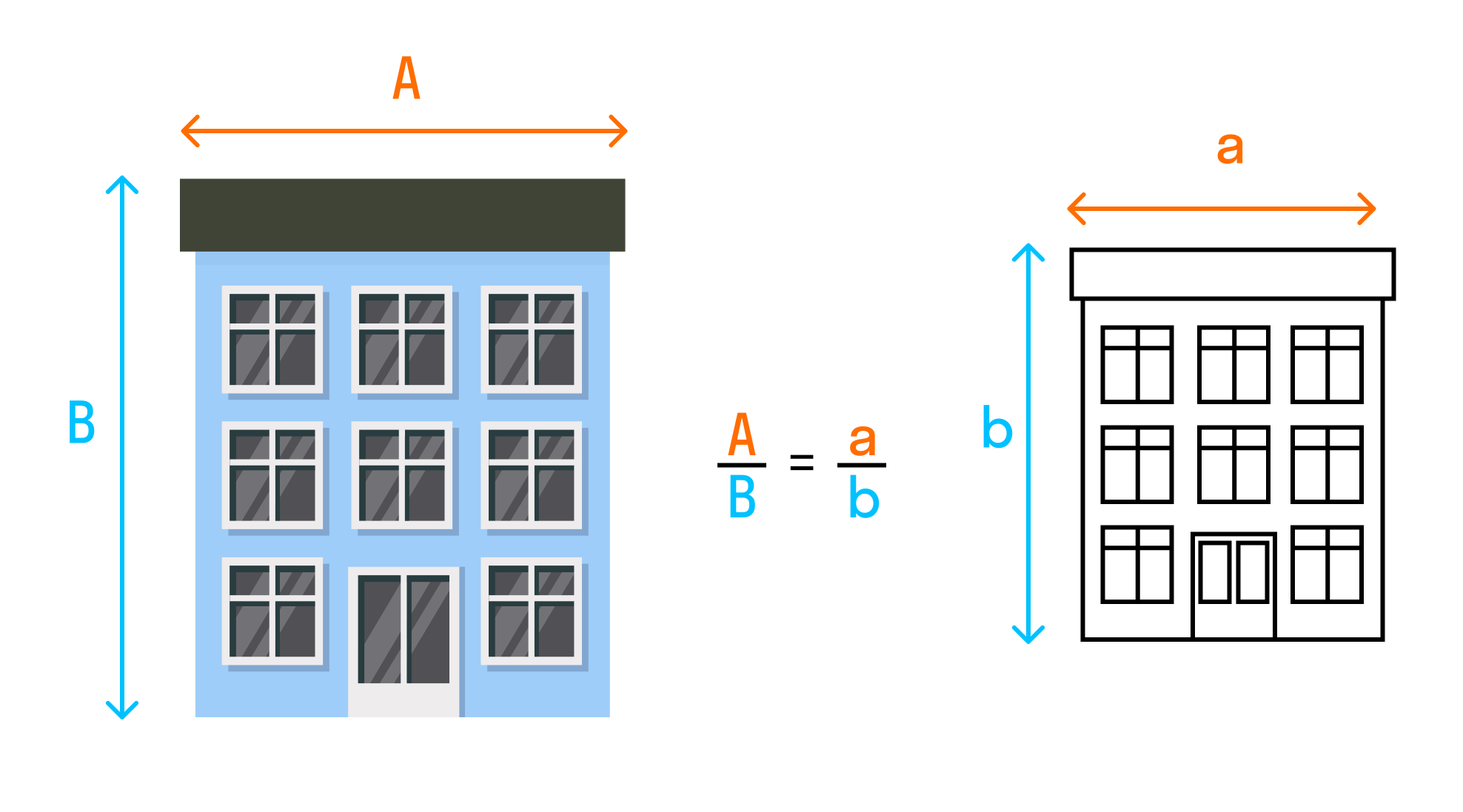
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
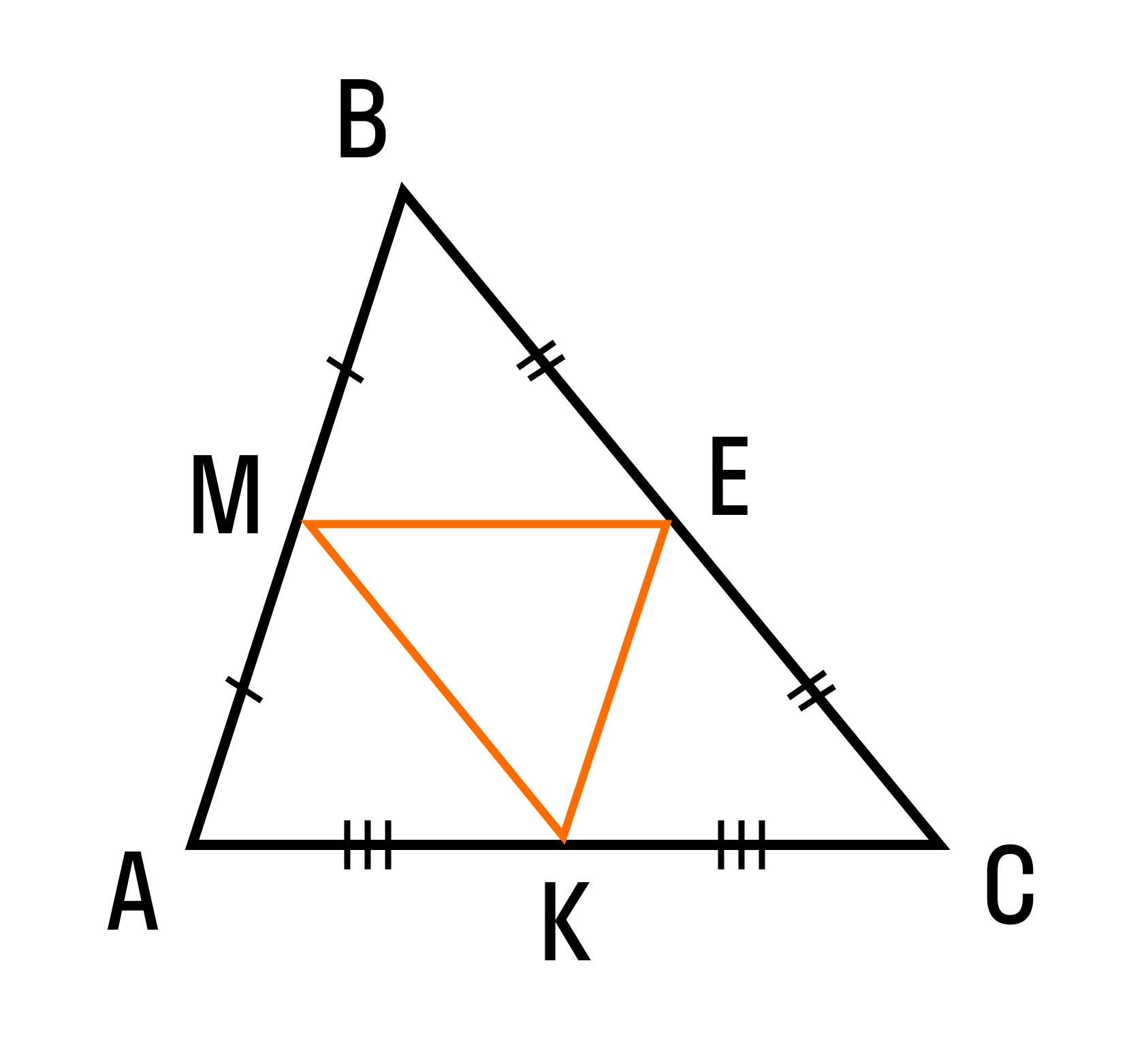
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
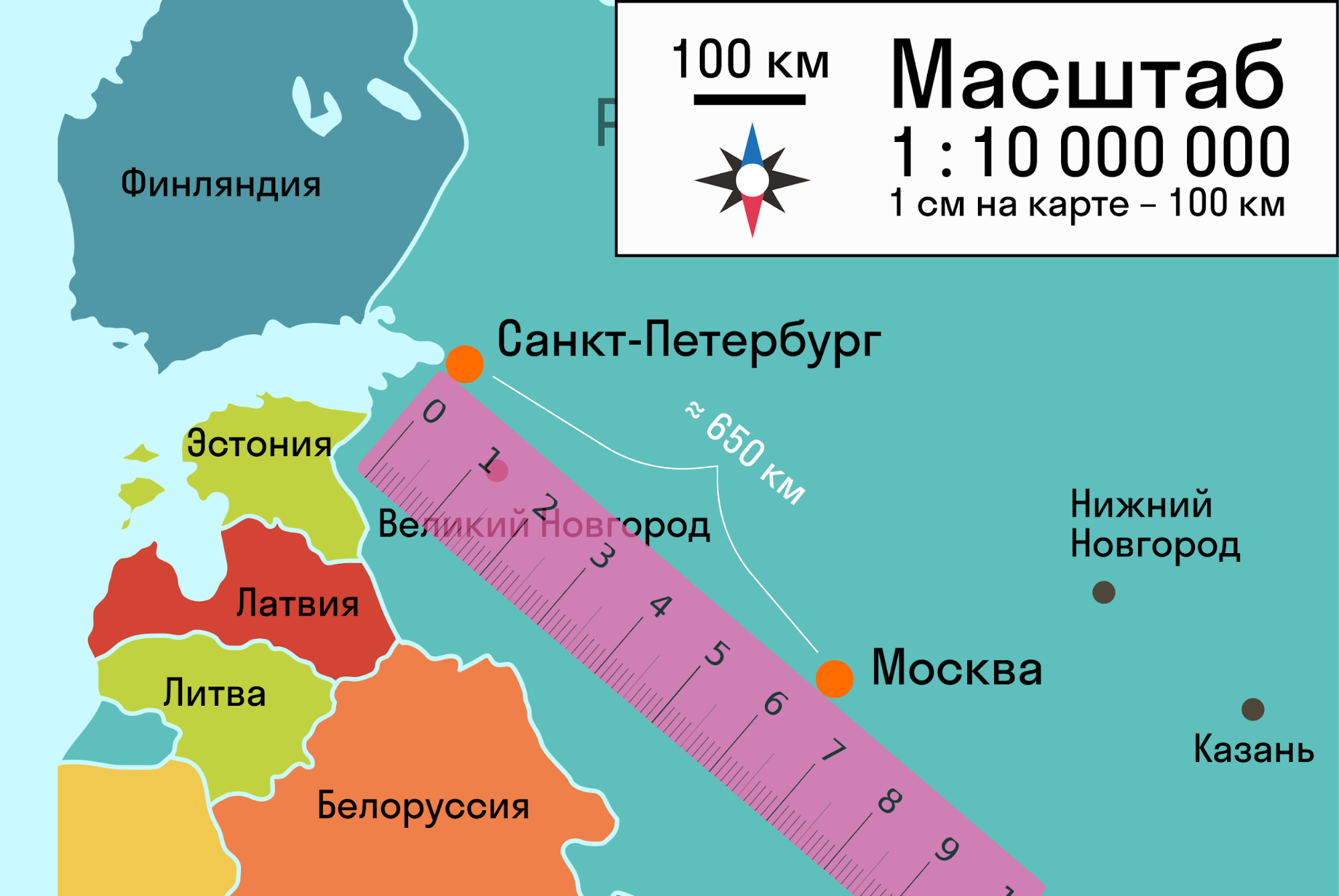
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
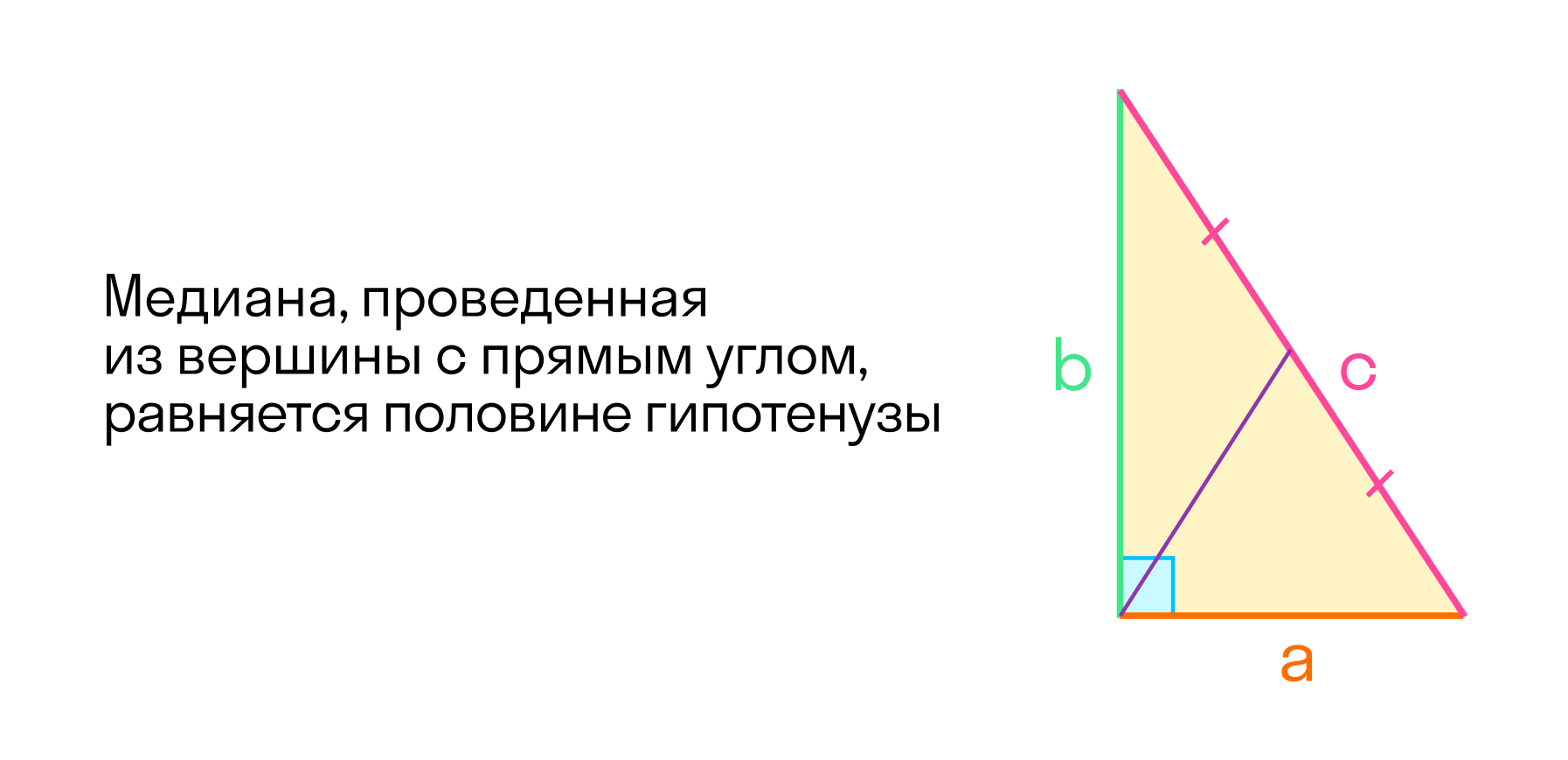
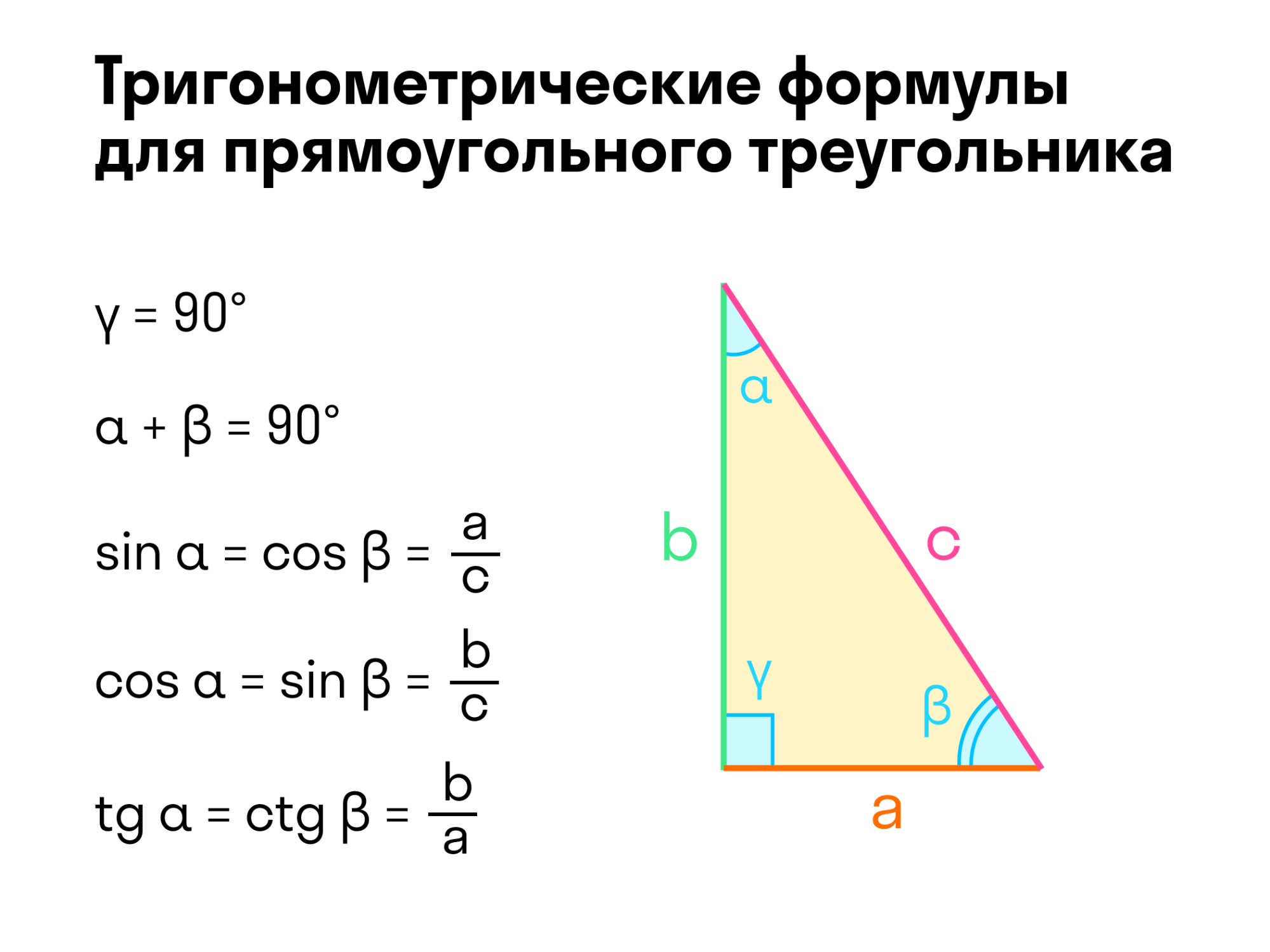
Свойства прямоугольного треугольника
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
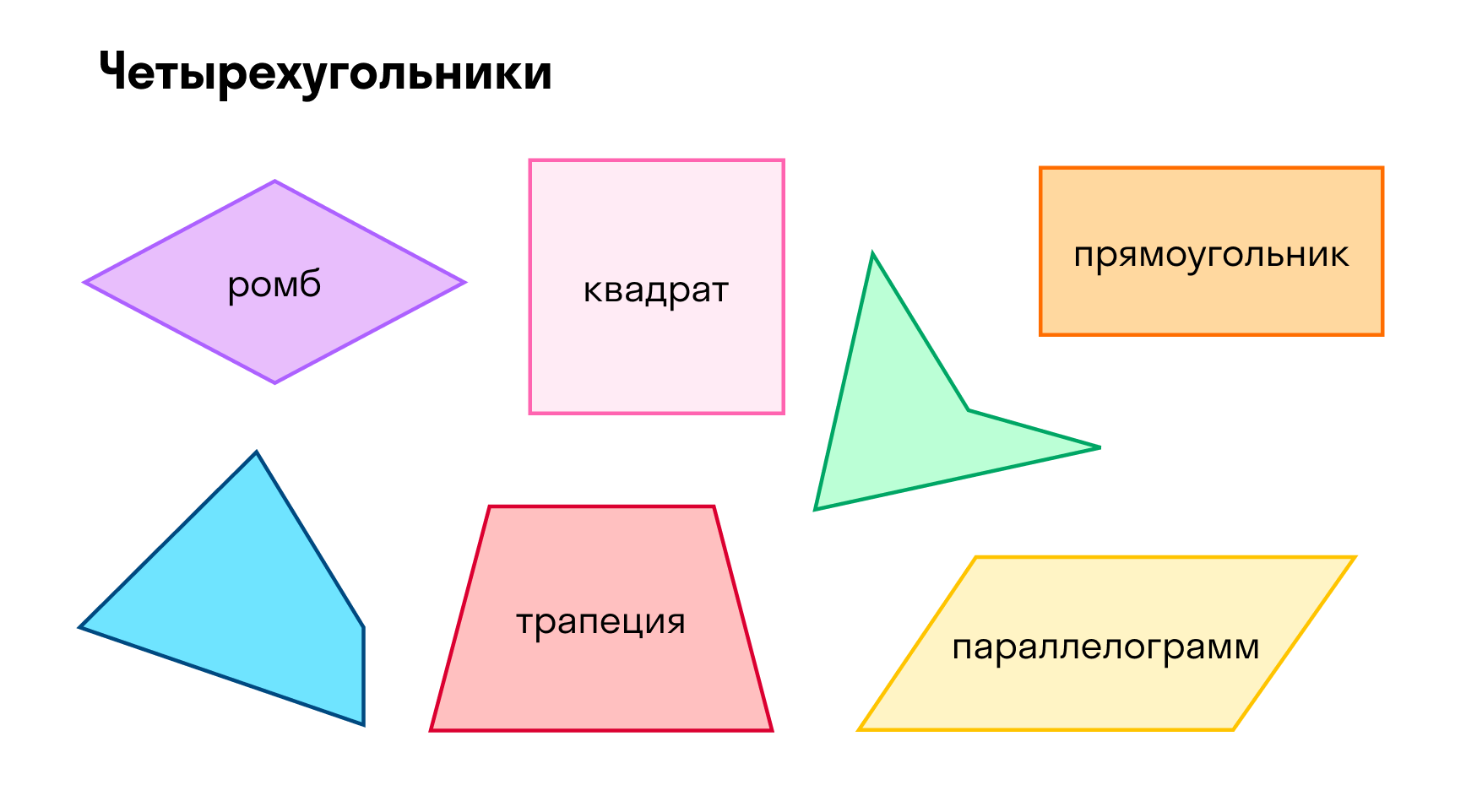
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
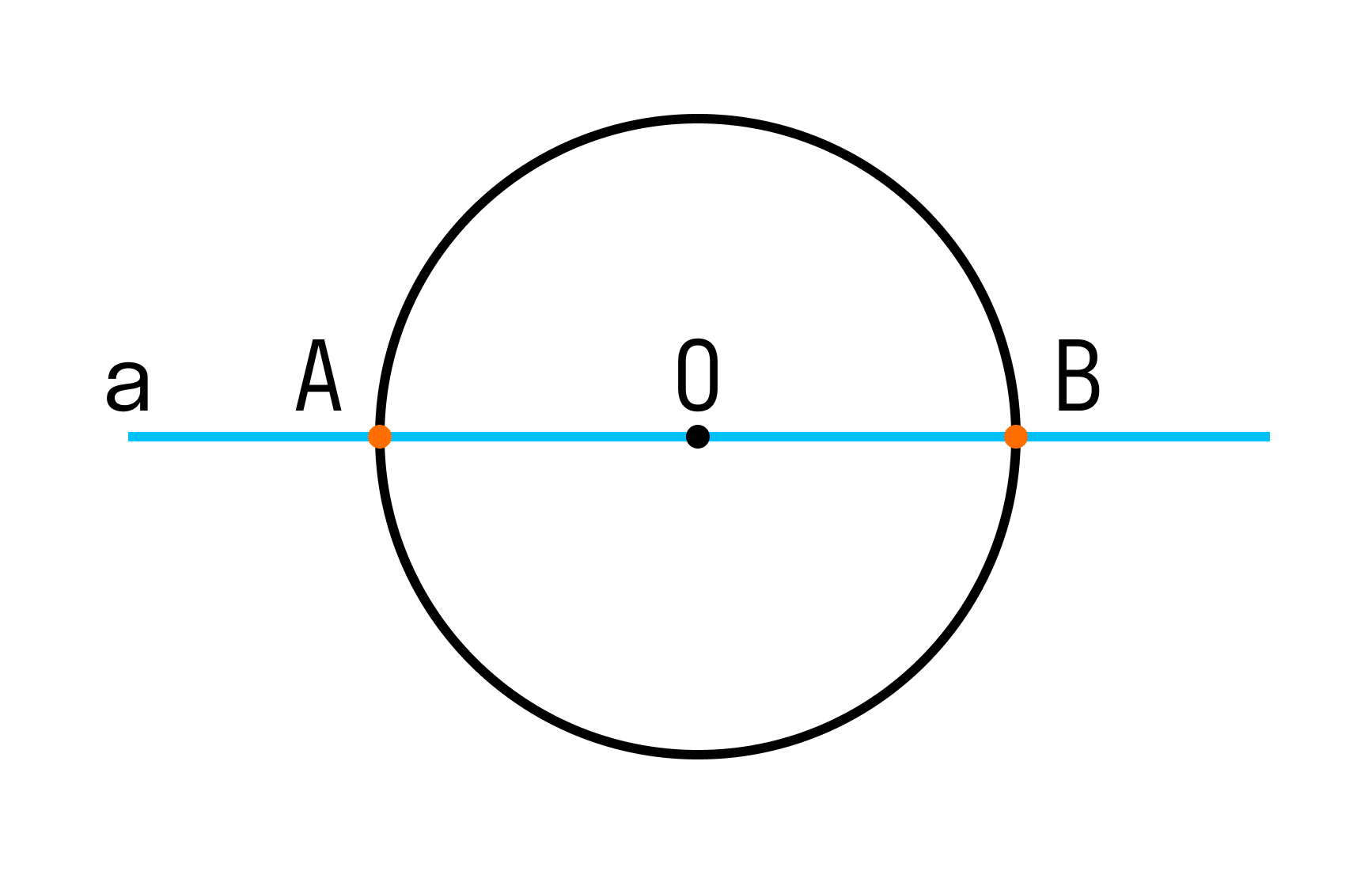
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
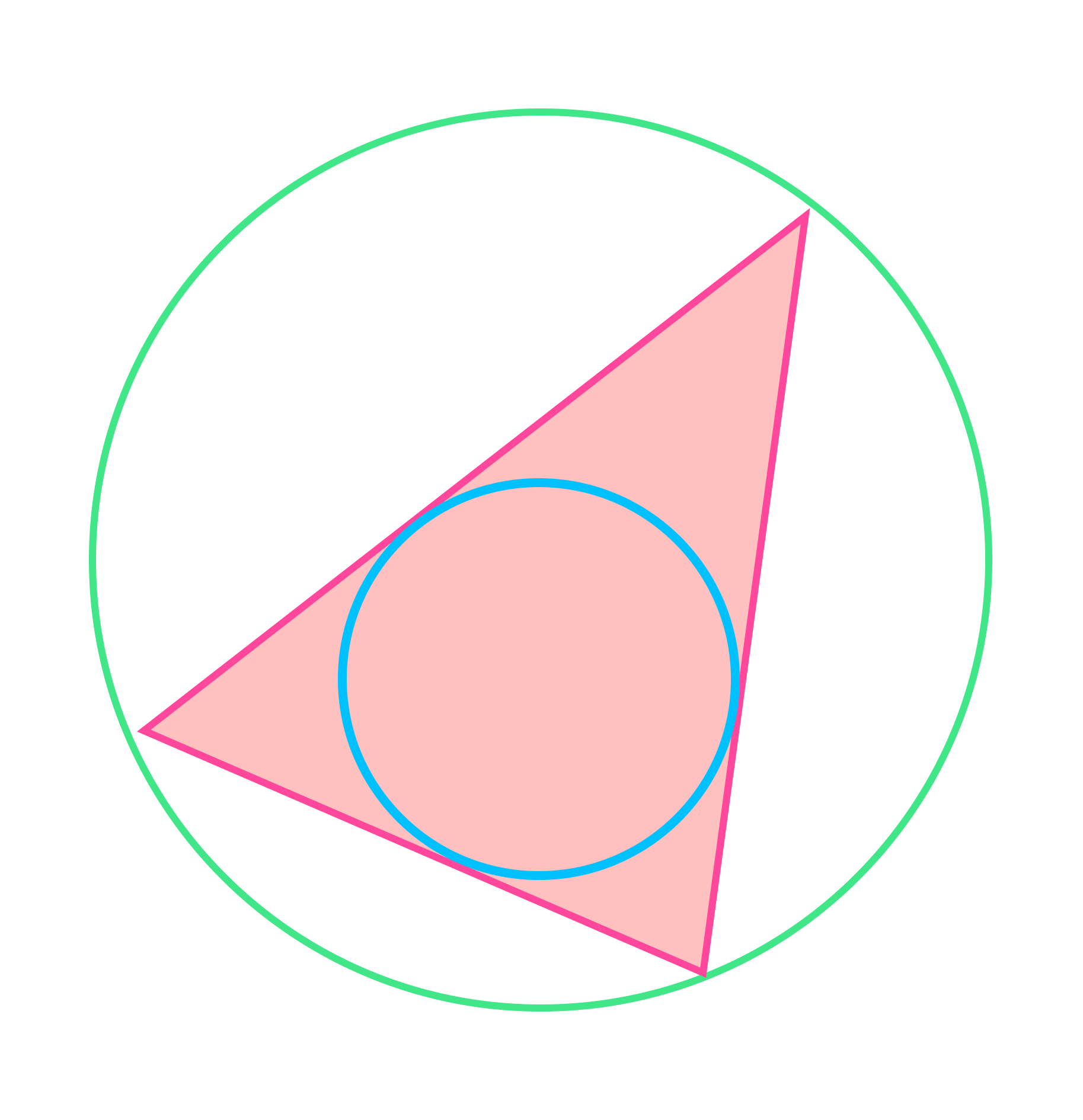
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
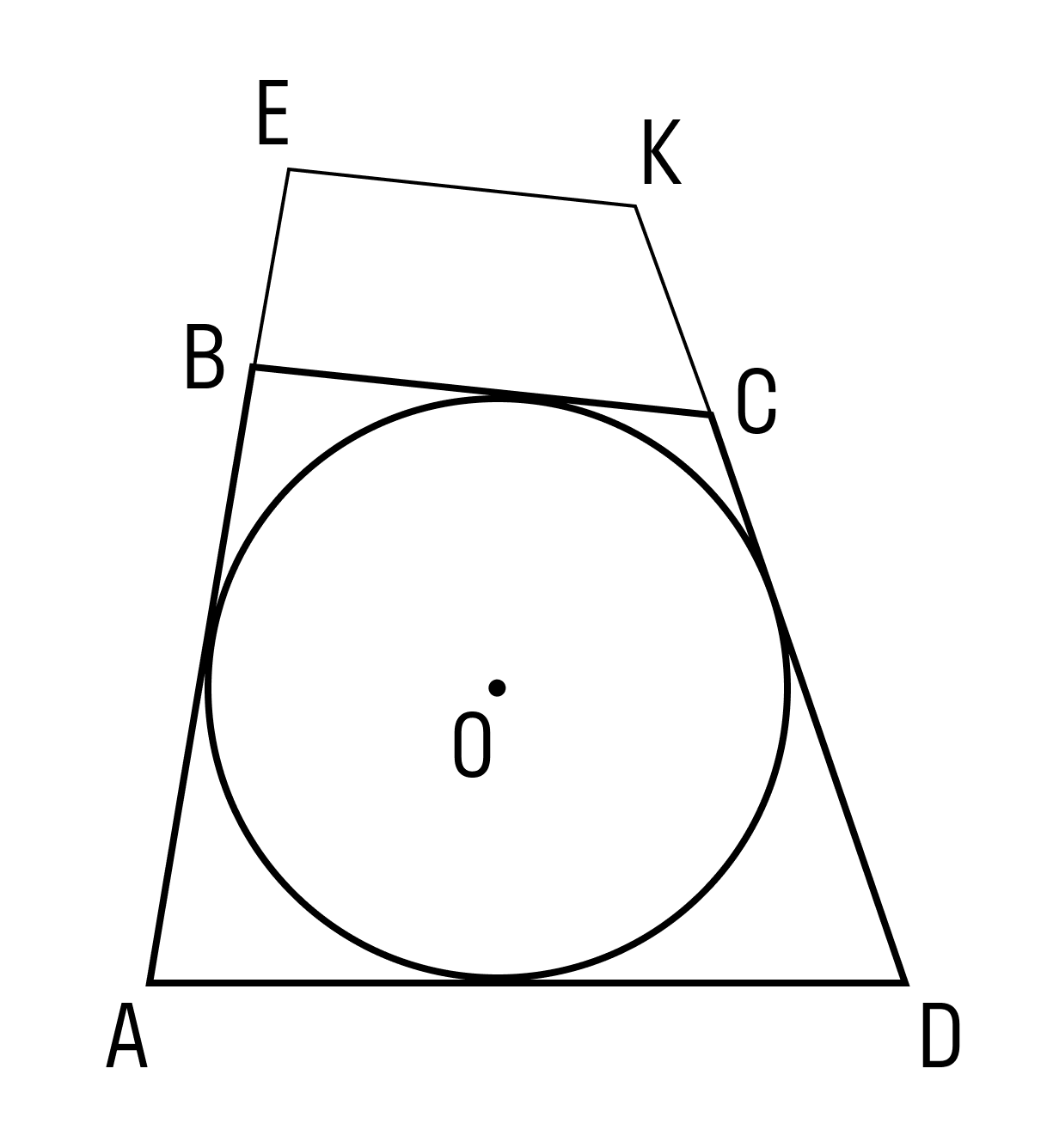
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.