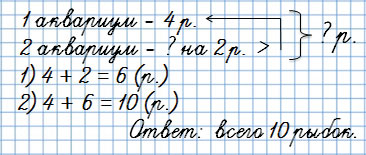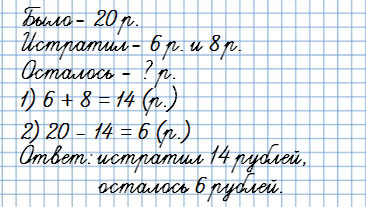Что такое пояснение к задаче
Памятка по математике «Краткая запись»
Краткая запись условия задач в 1-4 классе начальной школы
Для того, чтобы наглядно представить задачу и облегчить себе процесс ее решения, составляется краткая запись условия задачи. В краткой записи фиксируются величины, числа – данные и искомые, а также некоторые слова, показывающие, о чем говорится в задаче: «было», «положили», «стало» и т. п. и знаки, означающие отношения: «больше», «меньше», «одинаково» и т. п.
Краткую запись задачи можно выполнять в виде опорной схемы, таблицы, чертежа, с помощью геометрических фигур.
Для того чтобы краткая запись в максимальной степени способствовала решению задачи, нужно:
Основные виды краткой записи в начальной школе
Возможны вариации перечисленных вариантов краткой записи в зависимости от условия задачи. Возможна и запись в виде таблиц и рисунков.
— Витя собрал коллекцию из 18 камней и разложил на коробки поровну. Сколько камней в каждой банке?
Простая задача на деление на равные части, оформляем такие задачи в виде таблицы
В 1 коробке Количество коробок Всего камней
? к. 3 к. 18 к.
— 8 приглашений разложили в конверты, по 2 в каждый. Сколько использовали конвертов?
— Трое друзей решили сложится поровну и купить мяч стоимостью 60 рублей. Сколько денег должен дать каждый из них?
На 1 чел. денег Количество чел. Всего денег
поровну 3 чел. 60 руб.
— Одну деталь мастер должен делать за 45 мин, а делает за 38 мин. Сколько времени сэкономит мастер, когда он сделает 8 деталей?
Составная задача на разностное сравнение, лучше оформить в виде таблицы.
— Вера посадила 9 луковиц, по 3 луковицы в ряд. Сколько получилось рядов?
Это простая задача на деление по содержанию. Такую задачу нагляднее оформить картинкой.
— В детский сад привезли два бидона с молоком, по 20 л в каждом. За завтраком дети выпили 12 л молока. Сколько литров молока осталось?
Задача на нахождение остатка.
— В куске ткани было 24 м ткани. Из 10 м этой ткани сшили одинаковые детские костюмы, а из остальной ткани-7 одинаковых детских пальто. Сколько метров ткани расходовали на одно пальто.
— В парк привезли 33 куста роз. Когда на нескольких клумбах посадили по 6 кустов, то осталось еще 15 кустов. Сколько было клумб?
— В прятки играли 12 ребят. К ним присоединились 3 девочки и 4 мальчика. Сколько всего ребят стали играть в прятки?
— У Саши было 6 наклеек. Он подарил другу 2 наклейки. Потом Саша купил еще 5 наклеек. Сколько наклеек стало у Саши?
— На полянке паслись 14 коров, а овец на 10 больше. Сколько животных паслись на полянке?
— В первый день вырыли 5м траншеи, во второй на 3м меньше, чем в первый, в третий на 1м больше, чем во второй. На сколько больше вырыли траншей в первый и во второй день вместе, чем в третий?
— На двух полках было 17 кг меда. Со второй полки продали 5 кг и на 2 полках стало поровну. Сколько кг меда было на 1 полке?
Нагляднее представит задачу запись в виде схемы.
Пояснения к решению задач
Эта форма работы над составной задачей предусматривает проверку умения учащихся по данным действиям решения задачи пояснить, на какой вопрос и с какой целью отвечает действие. Таким образом, в конце каждого действия пишем пояснение, что именно мы нашли этим действием. Такая форма работы помогает учащимся увидеть другие отношения, вести необходимую цепочку логических рассуждений, анализировать и делать выводы.
Если использовались пояснения, ответ можно записать кратко. Если же не использовались, пишем полный ответ.
Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
Сколько грибов нашёл Володя?
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было. Стало. «
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было. Осталось. «
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали. Осталось. «
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Сколько рыбок в двух аквариумах?
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
Задачи с составлением рисунка по условию:
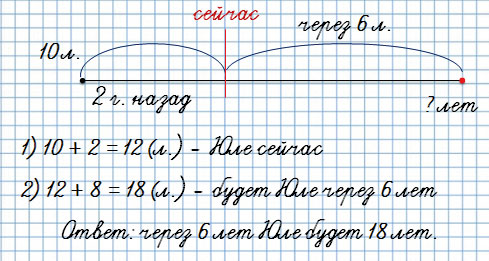
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Поделись с друзьями в социальных сетях:
Что такое пояснение для задачи?
Что такое пояснение для задачи?
Тоесть объяснить свои действия коротко и понятно.
Сколько таких платьев можно сшить из 48 м ткани?
(Реши задачу с пояснением).
Решил задачу по действиям с пояснениями и запиши ответ?
Решил задачу по действиям с пояснениями и запиши ответ.
Помогите написать пояснение к задачи №4?
Помогите написать пояснение к задачи №4.
Решите задачу с пояснениями?
Решите задачу с пояснениями.
Решите задачу с пояснениями?
Решите задачу с пояснениями.
В девяти одинаковых банках 20 кг крупы.
Сколько крупы в 27 таких банках?
Пожалуйста помогите?
С пояснением если можно.
Помогите со второй задачей по действиям и с пояснениями?
Помогите со второй задачей по действиям и с пояснениями.
6 задача помогите плищ прошу с пояснением?
6 задача помогите плищ прошу с пояснением.
Решите задачи?
Решите задачу с пояснениями подалуиста?
Решите задачу с пояснениями подалуиста.
Что такое пояснение к задаче
ОБРАЗОВАТЕЛЬНАЯ СИСТЕМА БУДУЩЕГО, ПРОВЕРЕННАЯ ПРОШЛЫМ
Этот сайт посвящен возрожденным классическим традициям образования.
С глубокой благодарностью к великим педагогам прошлого, оставившим нам это бесценное наследие.
АЛТУШКИНА ТАТЬЯНА АНАТОЛЬЕВНА
Руководитель проекта
Как перед многими мамами, передо мной когда-то встала проблема школьного обучения своих подросших детишек. Отдавать их в школу было безумно жалко. Я точно знала, что им там будет плохо, хотя и не могла тогда ясно сформулировать, почему…
ГОРЯЧЕВА ИРИНА АНАТОЛЬЕВНА
Разработчик филологического блока
Бывают ли в жизни чудеса.
В самом начале 2008 года мне позвонили из Екатеринбурга. За полторы тысячи километров от Москвы состоятельная многодетная мама, озадаченная образованием своих детишек, нашла мои публикации, посвящённые К. Д. Ушинскому, его учебным книгам, и обратилась ко мне за советами. Это был подарок свыше!
КОСТЕНКО ИГОРЬ ПЕТРОВИЧ
Разработчик математического блока, канд. физико-математич. наук, доцент
Более 140 опубликованных работ — научно-математических, научно-методических, историко-педагогических, в том числе учебник по теории вероятностей (изд. 2004 г. и 2012 г.) и монография «Проблема качества математического образования в свете исторической ретроспективы» (2013 г.).
НИФОНТОВА ЕЛИЗАВЕТА МИХАЙЛОВНА
Разработчик математического блока,
тренер-методист
Я работаю в Русской классической школе учителем математики и методистом уже более восьми лет. В эту школу я попала чудом, иначе не скажешь. Вспоминаю своё собеседование с учредителем школы — Татьяной Анатольевной.
БАЛАКАЕВ МИХАИЛ ГЕННАДЬЕВИЧ
Разработчик программ по истории
По образованию я юрист. Окончил Свердловский юридический институт по специальности «правоведение». После получения диплома работал в Институте философии и права УрО РАН. Потом судьба привела меня в школу, и я стал учителем истории.
МАЛЮГА НАТАЛЬЯ НИКОЛАЕВНА
Преподаватель начальной школы,
тренер-методист
Учителем начальных классов я работаю более 20 лет.
Начинала преподавать по программе традиционного обучения (математика М. И. Моро, Г. В. Бельтюкова; русский язык Т. Г. Рамзаевой, чтение М. И. Горецкого). Немного поработала и по программе «Школа 2100».
ШИПОВА НАТАЛЬЯ ВЯЧЕСЛАВОВНА
Преподаватель филологии,
тренер-методист
Выбрать профессию учителя — это взять на себя огромную ответственность за юные души твоих учеников, а учитель-словесник вдвойне в ответе за то, какими людьми станут его ученики, с каким отношением к жизни, к людям, к Родине они выйдут из школы.
КОЧЕВА НИНА ВАСИЛЬЕВНА
Педагог дошкольного и начального образования,
тренер-методист
Я начала работать по этой программе десять лет назад. За спиной у меня к этому времени был многолетний опыт работы в общеобразовательной школе. И я думаю, что именно он помешал мне сразу принять и оценить новую программу.
КОСТЕНКОВ ВЛАДИМИР АЛЕКСАНДРОВИЧ
Преподаватель
церковнославянского языка
По образованию я тренер-преподаватель. До работы в Русской классической школе был детским тренером по карате. Многого достиг как сам, будучи спортсменом, так и на тренерском поприще, и считал, что спорт — это призвание на всю мою жизнь…
ПЕТРОВА ГАЛИНА НИКОЛАЕВНА
Преподаватель филологии
По специальности я учитель английского и немецкого языков. В Русской классической школе работаю с 2011 года. Моё знакомство с РКШ началось с расписания уроков, которое я случайно увидела, будучи в гостях.
ВОЛКОВА ВЕРА БОРИСОВНА
Секретарь
Русской классической школы
Русская Классическая Школа стала частью моей жизни очень стремительно, буквально в течение одного дня.
Август 2012 года. Я уже полгода работаю секретарём в школе — приказы, документы, справки. А школа не обычная, средняя, а Русская классическая.
Решение простых линейных уравнений
Понятие уравнения
Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.
В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.