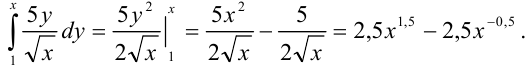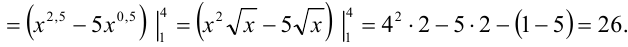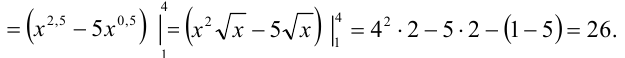Что такое повторный интеграл
Вычисление двойных интегралов: теория и примеры
Что значит вычислить двойной интеграл?
Записывается двойной интеграл так:
.
Случай прямоугольной области:
Случай криволинейной области:
Сведение двойного интеграла к повторному
Случай прямоугольной области
Пусть для такой функции существует двойной интеграл
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
.
Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид
.
Пример 1. Вычислить двойной интеграл
,
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл
,
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Случай криволинейной или треугольной области
.
Пусть для такой функции также существует двойной интеграл
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
.
Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид
.
Пример 3. Вычислить двойной интеграл
,
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования и видим, что она треугольная:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:
.
Вычисляем первое слагаемое:
Вычисляем второе слагаемое:
Вычисляем третье слагаемое:
Получаем сумму, которая и будет решением данного двойного интеграла:
.
Пример 4. Вычислить двойной интеграл
,
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
Пример 5. Вычислить двойной интеграл
,
если область D ограничена прямыми
.
Пример 6. Вычислить двойной интеграл
,
если область D ограничена прямыми
.
x-правильная и неправильная, y-правильная и неправильная области интегрирования
Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:
1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;
2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.
Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x-правильной
Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.
До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.
Вычисляется этот двойной интеграл так:
Смена порядка интегрирования
Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.
Пример 8. Сменить порядок интегрирования для повторного интеграла
.
(нижний) и 
(верхний).
Таким образом, после смены порядка интегрирования повторный интеграл запишется так:
.
После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.
Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.
Пример 9. Сменить порядок интегрирования для повторного интеграла
.
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.
Пример 10. Сменить порядок интегрирования для повторного интеграла
.
Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Для 
:
Для 
:
Для 
:
Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:
Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.
Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:
Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:
Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:
.
Вычисление площади и объёма с помощью двойных интегралов
Вычисление площади плоской фигуры с помощью двойного интеграла имеет более универсальный характер, чем вычисление площади криволинейной трапеции с помощью определённого интеграла. С помощью двойного интеграла можно вычислять площади не только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к к координатным осям.
.
Вычисляем внутренний (правый) интеграл:
.
Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Расставляя пределы интегрирования, получаем следующий повторный интеграл:
.
Вычисляем внутренний (правый) интеграл:
.
Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Так что же такое двойной интеграл?
,
которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.
Определение. Если интегральная сумма при неограниченном возрастании числа n разбиений области D и стремлении наибольшего из диаметров частичных областей к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. Обобщением понятия двойного интеграла для функции трёх переменных является тройной интеграл.
Понятие повторного интеграла
Вычислять двойные интегралы как пределы интегральных сумм весьма затруднительно, поэтому возникает естественная задача о разработке техники двойного интегрирования, минуя непосредственное суммирование и предельный переход.
Важнейшим результатом в этом направлении является формула сведения двойного интеграла к повторному. Определим понятие повторного интеграла.
Пусть на отрезке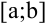 
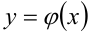
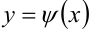
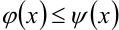
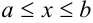
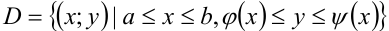
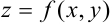
заданы непрерывные функции 
и 
такие, что 
, 
, и пусть на области 
(рис.29.1.) определена функция 
.
Если для любого фиксированного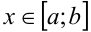 
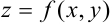
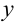
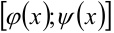
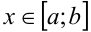
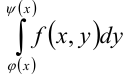
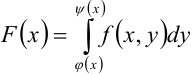
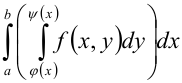
функция , как функция переменной 
, интегрируема на отрезке 
, т.е. при любом существует интеграл 
, и функция 
интегрируема на отрезке , то интеграл 
называется повторным интегралом и
обозначается через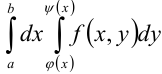 
.
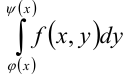
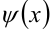
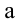
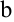
При этом называется внутренним интегралом; 
и 
— внутренними, 
и 
— внешними пределами интегрирования. Если внутренние пределы интегрирования в повторном интеграле могут быть как постоянными, так и переменными, то внешние пределы постоянны всегда.
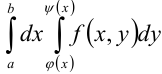
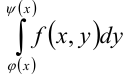
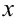
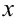
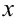
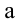
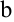
Для вычисления повторного интеграла надо последовательно взять два обычных определенных интеграла. Сначала берется внутренний интеграл , в котором переменная 
считается постоянной. Затем берется внешний интеграл, т.е. полученное выражение, зависящее от , интегрируется по от до .
Рассмотрим пример вычисления повторного интеграла.
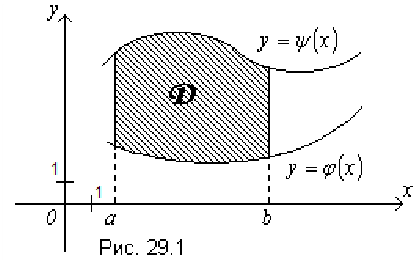
Пример №29.1.
Вычислите повторный интеграл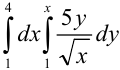 
.
Решение:
Сначала найдем внутренний интеграл, считая 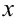постоянным:
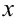
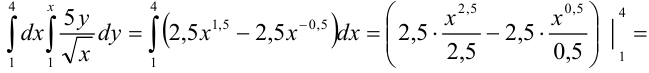
Затем найдем внешний интеграл, т.е. полученную функцию проинтегрируем по . Тогда
Для сокращения записи все вычисления можно записать следующим образом:
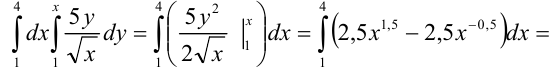
Ответ: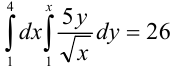 
.
Следует заметить, что для функции , определенной на области 
понятие повторного интеграла вводится аналогично рассмотренному ранее. При этом повторный интеграл обозначается через 
.
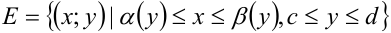
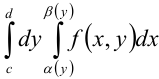
Здесь при вычислении внутреннего интеграла постоянной считается переменная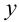 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
ПОВТОРНЫЙ ИНТЕГРАЛ
Найдено 24 изображения:
ПОВТОРНЫЙ ИНТЕГРАЛ, понятие интегрального исчисления. Вычисление двойного интеграла
где при вычислении внутреннего интеграла х считается постоянным. Таким образом, вычисление двойного интеграла сводится к двум вычислениям обычных интегралов, или, как говорят, к П. и. Геометрически сведение двойного интеграла к П. и. означает возможность вычисления объёма цилиндроида как путём разбиения его на элементарные столбики, так и путём разбиения его на элементарные слои, параллельные плоскости yOz. При нек-рых условиях на функцию f(x, у) и область S в П. и. можно изменить порядок интегрирования (то есть сначала интегрировать по х, а потом по у). Аналогично определяется П. и. в случае функций большего числа переменных. Лит. см. при ст. Интегральное исчисление.
интеграл, в к-ром последовательно выполняется интегрирование по разным переменным, т. е. интеграл вида
существуют и равны между собой:
Множество же всегда измеримо относительно меры my, если только множество Аизмеримо относительно меры m.
Сформулированные условия возможности перемены порядка интегрирования в П. и. являются лишь достаточными, но не необходимыми: иногда перемена порядка интегрирования в П. и. допустима, а соответствующий кратный интеграл не существует.
Напр., для функции при x 2 +y 2 >0 и f(0, 0) = 0 П. и.
а кратный интеграл
не существует. Однако если существует хотя бы один из интегралов
то функция f интегрируема на множестве и справедливо равенство (2).
Лит.:[1] Ильин В. А., Полняк Э. Г., Основы математического анализа, 2 изд., ч. 2, М., 1980; [2] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [3] Кудрявцев Л. Д., Курс математического анализа, т. 2, М., 1981; [4] Никольский С. М., Курс математического анализа, 2 изд., т. 2, М., 1975; [5] Смирнов В. И., Курс высшей математики, т. 5, М., 1959. Л. Д. Кудрявцев.