Что такое поверхность многогранника
Что такое многогранник? Примеры
Примеры многогранников:
1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);
Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.
Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.
Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.
Популярное
Предположим, вы впервые увидели на прилавке книжного магазина или на страницах в интернете издание «Волшебные грани». Хочется попробовать? Но вот вопрос, какой выпуск взять на пробу.
Почему бумага? Иногда приходится слышать вопрос: «Почему вы выбрали для сборки многогранников такой материал как бумага (или точнее дизайнерский картон)? Это же.
Монумент «Звезда Кеплера» (норв. Keplerstjernen), высотой 45 метров, расположен недалеко от города Осло (Норвегия) в окрестностях аэропорта.
Интересный лайфхак, прислала наша читательница из Республики Беларусь.
Можно ли представить икосаэдр в виде более простых многогранников.
Большая Энциклопедия Нефти и Газа
Развертка поверхности многогранников известна читателю из средней школы. [4]
Площадью поверхности многогранника называется сумма площадей всех его граней. [5]
Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью всех его граней. Развертывание гранных поверхностей выполняют для-проведения раскроя листового материала при изготовлении деталей или определения площади поверхности деталей, покрываемых различными материалами. Определение площади важно при различных покрытиях, выполняемых как с декоративными целями, так и с целью придания поверхности определенных свойств, например повышенной электропроводности, а также при различных химических методах обработки поверхностей. [6]
Площадью поверхности многогранника называется сумма площадей всех его граней. [7]
Разверткой поверхности многогранника называется плоская фигура, полученная при совмещении всех его граней с плоскостью. [9]
Развертка поверхности многогранников известна читателю из средней школы. Поэтому на этом вопросе мы останавливаемся кратко, только в плане повторения известных ранее сведений. [10]
Разверткой поверхности многогранника называют плоскую фигуру, полученную в результате совмещения с плоскостью чертежа всех граней многогранника. [12]
Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью всех его граней. Развертывание гранных поверхностей выполняют для проведения раскроя листового материала при изготовлении деталей или определения площади поверхности деталей, покрываемых различными материалами. [13]
Площадью поверхности многогранника называется сумма площадей всех ограничивающих его многоугольников. [14]
math4school.ru
Многогранники
Основные понятия

Некоторые пространственные фигуры, изучаемые в стереометрии, называют телами или геометрическими телами. Наглядно тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
Многогранником называется геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников.

Выпуклым называется многогранник, если он расположен по одну сторону плоскости, проведённой через любой многоугольник, образующий поверхность данного многогранника.
Многоугольники, составляющие поверхность многогранника, называются его гранями; стороны многоугольников – рёбрами; вершины – вершинами многогранника:
Теорема Эйлера для многогранников:
Если V — число вершин выпуклого многогранника, R — число его ребер и G — число граней, то верно равенство:
Призма

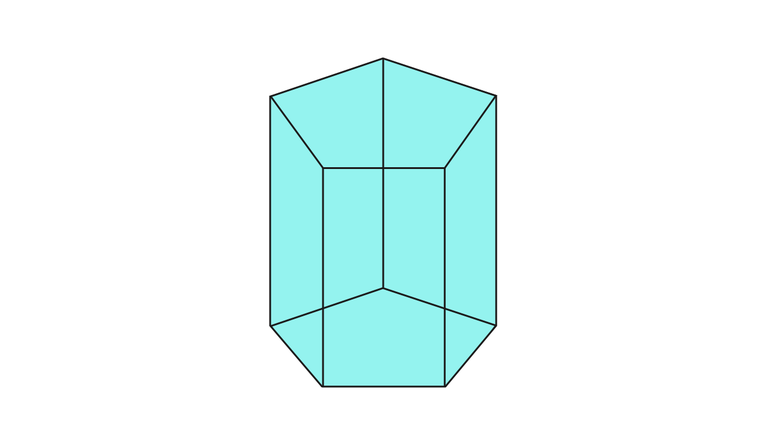
Призмой называется многогранник, состоящий из двух плоских многоугольников, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники, о которых шла речь, называются основаниями призмы, а отрезки, соединяющие их соответствующие вершины – боковыми рёбрами призмы.
Основания призмы равны и лежат в параллельных плоскостях.
Боковые рёбра призмы равны и параллельны.
Поверхность призмы состоит из двух оснований и боковой поверхности.
Боковая поверхность любой призмы состоит из параллелограммов, у каждого из которых две стороны являются соответствующими сторонами оснований, а две другие – соседними боковыми рёбрами.
Высотой призмы называется любой из перпендикуляров, проведённых из точки одного основания к плоскости другого основания призмы.
A1О – высота призмы;
α – угол наклона бокового ребра к основанию призмы.

Призма называется прямой, если её рёбра перпендикулярны плоскостям оснований. В противном случае призма называется наклонной.
Боковые грани прямой призмы – прямоугольники.
Боковое ребро прямой призмы является её высотой.
Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы:
Прямая призма называется правильной, если её основания являются правильными многоугольниками.

Сечения призмы плоскостями, параллельными боковым рёбрам,являются параллелограммами. В частности, параллелограммами являются диагональные сечения. Это сечения плоскостями, проходящими, через два боковых ребра, не принадлежащих одной грани:
ВВ1D1 D – диагональное сечение.
Если в произвольной наклонной призме провести сечение, перпендикулярное боковым рёбрам и пересекающее все боковые рёбра, и площадь этого сечения обозначить S⊥, а периметр – Р⊥, тогда:
В любой призме площадь полной поверхности считается как сумма площади боковой поверхности и удвоенной площади основания:
Параллелепипед

Призма, в основании которой лежит параллелограмм, называется параллелепипедом.
У параллелепипеда все грани – параллелограммы.
Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
У параллелепипеда противолежащие грани параллельны и равны.
Диагональю параллелепипеда, как и многогранника вообще, называется отрезок, соединяющий вершины параллелепипеда, не лежащие в одной его грани.
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Точка пересечения диагоналей параллелепипеда является его центром симметрии.

Прямоугольным параллелепипедом называется такой прямой параллелепипед, в основании которого лежит прямоугольник.
Все грани прямоугольного параллелепипеда являются прямоугольниками.
Длины рёбер прямоугольного параллелепипеда, выходящих из одной вершины, называются его измерениями или линейными размерами.
У прямоугольного параллелепипеда три измерения.
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений:
В прямоугольном параллелепипеде верно:


В прямоугольном параллелепипеде, как и во всяком параллелепипеде, есть центр симметрии – точка пересечения его диагоналей. У него есть также три плоскости симметрии, проходящие через центр симметрии параллельно парам противолежащих граней. На первом рисунке, приведённом выше, показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда.
Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме трёх названных.
Если же у параллелепипеда два линейных размера равны, то есть он является правильной четырёхугольной призмой, то у него есть еще две плоскости симметрии. Это плоскости диагональных сечений, показанные на втором рисунке.

Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.
Диагональ куба в квадратный корень из трёх раз больше его стороны:

Четыре сечения куба являются правильными шестиугольниками (одно из них показано на рисунке) – эти сечения проходят через центр куба перпендикулярно четырём его диагоналям.
У куба девять плоскостей симметрии:
Пирамида
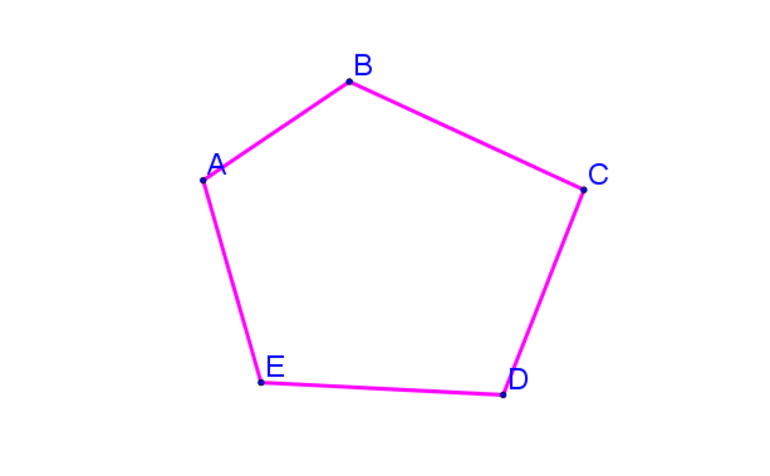
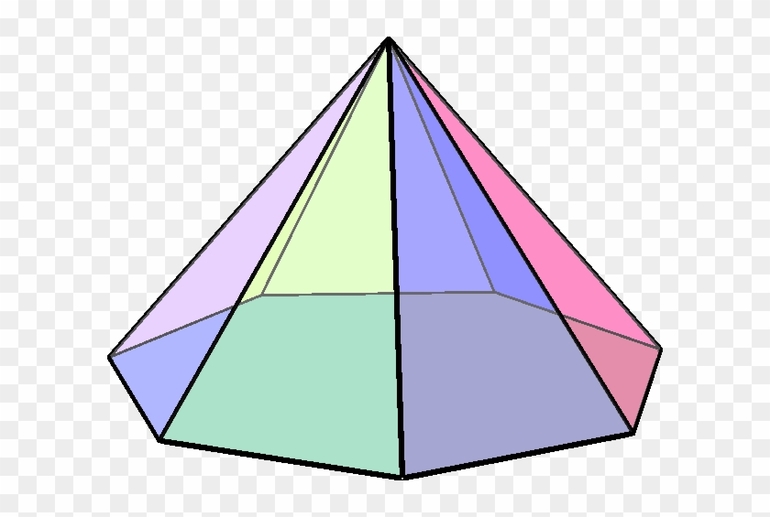
Пирамидой (например, SABCDE ) называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE ) – основания пирамиды, точки ( S ), не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
Поверхность пирамиды состоит из основания (пятиугольник ABCDE ) и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды:
Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.
Высотой пирамиды ( SО ) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания.
α – угол наклона бокового ребра SA пирамиды к плоскости её основания;
β – угол наклона боковой грани ( SED ) пирамиды к плоскости её основания.
Основание высоты пирамиды является центром окружности, описанной около основания пирамиды, тогда и только тогда, когда выполняется одно из условий:
Основание высоты пирамиды является центром окружности, вписанной в основание пирамиды, тогда и только тогда, когда выполняется одно из условий:
Объём пирамиды равен трети произведения площади основания на высоту пирамиды:
Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания:
Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды.

Плоскость, которая пересекает пирамиду и параллельна её основанию, делит её на две части:
многогранник, называемый усеченной пирамидой ( AВСA1В1С1 ).
Основания усеченной пирамиды представляют собой подобные многоугольники, боковые грани – трапеции.
Высота усеченной пирамиды ( ОО1 ) – это расстояние между плоскостями её оснований.
Если S1 и S2 – площади оснований усечённой пирамиды и h – её высота, то для объёма усеченной пирамиды верно:

Пирамида (например, SABCD ) называется правильной, если ее основанием является правильный многоугольник ( ABCD – квадрат ), а основание высоты совпадает с центром этого многоугольника ( О – центр описанной и вписанной окружностей основания).
Осью правильной пирамиды называется прямая, содержащая ее высоту.
Боковые ребра правильной пирамиды равны.
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды ( SL ), проведенная из ее вершины к стороне основания, называется апофемой.
Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему:

Усеченная пирамида (например, АВСDA1В1С1D1 ), которая получается из правильной пирамиды, также называется правильной.
Правильные многогранники


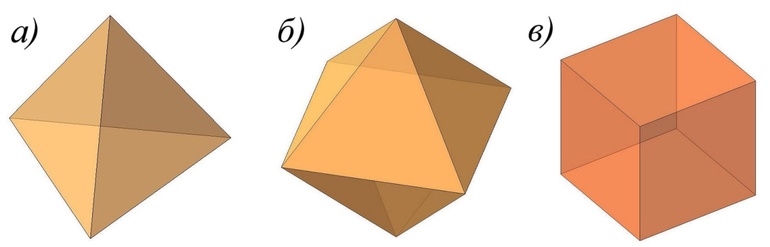
Тетраэдр Куб Октаэдр


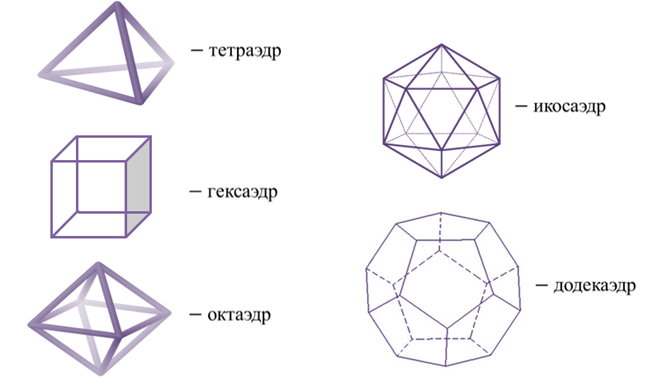
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
У куба (правильный гексаэдр) все грани – квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами.
У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.
У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.
У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.
Основные понятия
Определение многогранника включает в себя такое понятие, как геометрическое тело, созданное из плоских многоугольников. Их число конечное. От формы каждого из них напрямую зависят свойства итоговой фигуры. Их делят на 2 типа:
Поскольку многогранники рассматриваются в трехмерном евклидовом пространстве, они относятся к стереометрии. А их многоугольники лежат в двумерной плоскости, что относится к планиметрии. Поэтому основные свойства и понятия формируются, включая в себя обе эти науки.
Параметры фигуры
Правильные многогранники
Правильные многогранники — фигуры, грани которых представляют собой многоугольники с равными углами и сторонами. Также они называются Платоновыми телами. Всего существует 5 соответствующих тел, подробные характеристики которых представлены в таблице.
Правильные многогранники изучались древними греками. Однако первые модели в орнаменте и по отдельности появились намного раньше. Например, археологами были найдены вырезанные каменные шары в Шотландии, которые датируются поздним неолитом (соответственно, за 1000 лет до жизни и деятельности Платона).
Призма и ее особенности
Геометрическое тело называют прямым, если каждое ребро лежит перпендикулярно основанию. Также они становятся высотами. Когда грани идентичны, многоугольник считается правильным, и его диагональное сечение образует параллелограмм.
Характеристики параллелепипеда
Параллелепипед — многогранник, основанием и гранями которого является параллелограмм. Фигура характеризуется как неправильная. Основные характеристики:
Когда все грани параллелограмма являются прямоугольными, фигура характеризуется, как прямоугольная. Длина каждого ребра считается линейным размером. У такой фигуры есть три измерения. При этом справедлива формула d² = a² + b² + c². При расчетах руководствуются и другими. Для объема : V = abc, для площади многогранника: S=2·(ab+ bc +ac).
Пирамида и ее величины
Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:
Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.
Понятие многогранника
Урок 25. Геометрия 10 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Понятие многогранника»
Начиная изучать стереометрию, мы говорили, что все геометрические тела делятся на два больших класса тела вращения и многогранники, с некоторыми многогранниками мы с вами уже знакомы. Напомним, какие фигуры мы назвали тетраэдром и параллелепипедом. Мы уже с вами познакомились со свойствами этих фигур.
Сегодняшний наш урок открывает раздел, в котором мы познакомимся с другими многогранниками, но прежде давайте вспомним основные понятия, связанные с многогранниками.
Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.
Многогранник – это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
Это тело также называется многогранником.
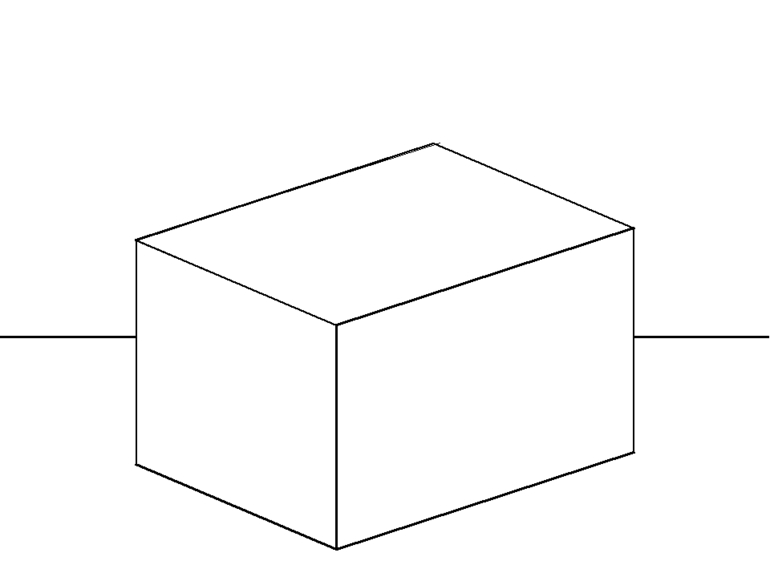
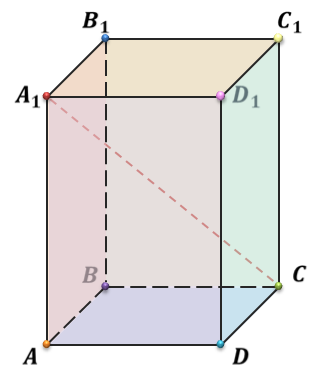
Обратим внимание, из чего состоит поверхность многогранника. Давайте рассмотрим, например, прямоугольный параллелепипед ABCDA1B1C1D1.
Как уже говорилось ранее, поверхность прямоугольного параллелепипеда состоит из шести прямоугольников. Т.е. его поверхность составлена из шести многоугольников. Назовем их: ABCD, A1B1C1D1, AA1B1B, DD1C1C, AA1D1D и BB1C1C. Многоугольники, из которых составлен многогранник, называют его гранями. Заметим, что никакие две соседние грани многогранника не лежат в одной плоскости.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, например, A1C – называется диагональю многогранника. В данном случае, диагональ прямоугольного параллелепипеда.
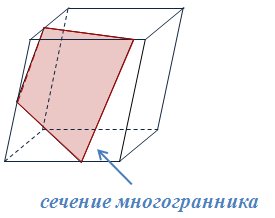
Плоскость, по обе стороны от которой имеются точки многогранника, называется секущей плоскостью, а общая часть многогранника и секущей плоскости – сечением многогранника.
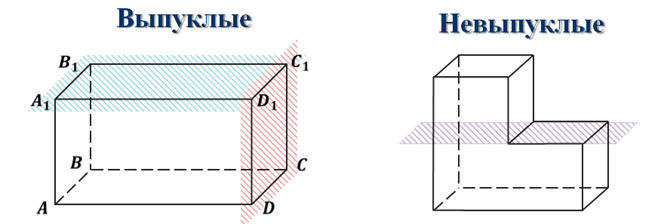
Многогранники, также как и многоугольники бывают выпуклыми и невыпуклыми.
Так, если провести плоскость, например, через грань DD1C1C, то весь многогранник будет лежать по одну сторону от этой плоскости. Аналогично, если провести плоскости и через остальные его грани, многогранник всегда будет расположен по одну сторону от этих плоскостей. Такой многогранник называется выпуклым.
Определение. Многогранник называется выпуклым, если он лежит по одну сторону от плоскости каждой своей грани.
Если это условие не выполняется, т.е. многогранник лежит по разные стороны хотя бы от одной плоскости, проходящей через грань, то многогранник называется невыпуклым.
Легко заметить, что все грани выпуклого многогранника являются выпуклыми многоугольниками. Отметим, что в выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360°.
Пояснить это утверждение нетрудно. Возьмем многогранник и разрежем его вдоль ребер и все его грани с общей вершиной А развернуты так, что они оказались расположенными в одной плоскости α. Очевидно, что сумма всех плоских улов при вершине А меньше 360°.
А теперь давайте немного окунемся в историю.
Огромный вклад в развитии математики в целом и геометрии в частности внесли философские школы, в которых происходит постепенный переход от практической к теоретической геометрии.
Одной из самых первых и самых известных геометрических школ была пифагорейская, она существовала в VI-V вв. до нашей эры. Названа она была в честь своего основателя древнегреческого ученого Пифагора.
Пифагорейцы использовали правильные многогранники для философских теорий. Так огню они придавали форму тетраэдра (пирамиды), земле – форму гексаэдра (куба), воздуху – форму октаэдра (фигуры, которая образована восьмью равносторонними треугольниками), воде – форму икосаэдра (фигуры, которая образована двадцатью равносторонними треугольниками). По их мнению вся вселенная имеет форму додекаэдра (фигуры, которая состоит из двенадцати правильных пятиугольников).
Но математикой в целом и геометрией в частности интересовались не только ученые. Существует так называемое математическое искусство Эшера.
Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.
Правильные геометрические тела — многогранники — имели особое очарование для Эшера. Во многих его работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.
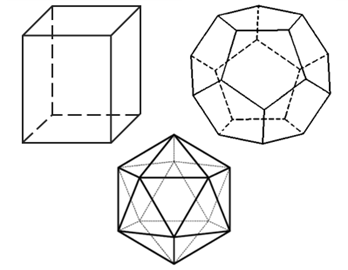
Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.
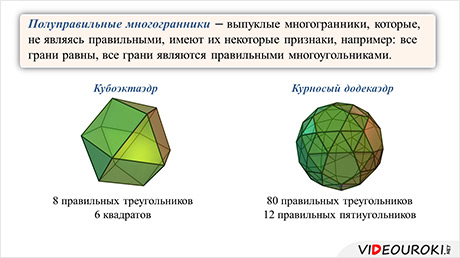
Помимо правильных многогранников существуют так называемые полуправильные многогранники. Это выпуклые многогранники, которые, не являясь правильными, имеют их некоторые признаки, например: все грани равны, все грани являются правильными многоугольниками. К таким фигурам относятся например кубоэктаэдр – фигура, гранями которой являются восемь правильных треугольников и шесть квадратов, или, например, курносый додекаэдр – фигура, которая состоит из восьмидесяти правильных треугольников и двенадцати правильных пятиугольников. Подобных многогранников существует двадцать шесть.
Закончить наш сегодняшний урок хочется словами советского математика Лазаря Ароновича Люстерника «Теория многогранников, в частности выпуклых многогранников,— одна из самых увлекательных глав геометрии».