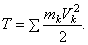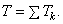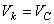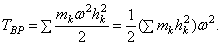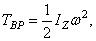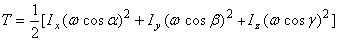Что такое потенциальные силовые поля
Что такое потенциальные силовые поля
Потенциальное силовое поле. Силовая функция и потенциальная энергия поля. Поверхности уровня и их свойства.
Свойства поверхностей уровня.
Из лекций:
Силовым полем называют часть пространства в каждой точке которого на материальную точку действует сила зависящая от координат.
Например, в декартовой системе координат: U(x,y,z,t)
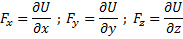
Вектор-градиент скалярной величины:
Основные свойства U стационарного потенциального силового поля.
Полная работа силы не зависит от пути перемещения.
Полная работа силы поля на каком-либо перемещении равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории (если силовая функция является однозначной) (при нестационарном поле это определение полной работы не действует).
Частный случай: Работа силы потенциального силового поля равна нулю, при перемещении точки по замкнутой траектории.
Потенциальной энергией (П) потенциального силового поля (ПСП) в заданной точке называется работа, которую совершают силы поля при перемещении материальной точки из данной точки в начальную.
Для всех точек U0=const одинаковое.
Потенциальную энргию какой либо точки ПСП с точностью до константы можно определить как значение U в этой точке со знаком «минус» (-U).
Свойства поверхностей уровня:
1) Работа силы равна нулю, если начальные и конечные точки перемещения лежат на одном уровне.
2) Сила потенциального силового поля (ПСП) всегда перпендикулярна плоскости касательной к поверхности уровня.
3) Сила всегда направлена в сторону возрастания силовой функции.
4) Если поверхности уровня сближаются, то сила возрастает.
Потенциальное силовое поле и потенциальная энергия



Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определенная сила, зависящая от координат точки и времени (стационарный и нестационарный случаи).
Силовое поле называют потенциальным, если имеется силовая функция 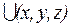
Силовая функция определяется с точностью до постоянной, так как добавка в виде константы под знак частной производной не влияет на значения Fx, Fy, Fz.
Запишем работу силы потенциального силового поля:
Элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции.
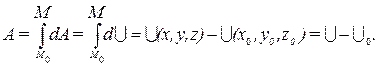
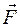
Эта работа не зависит от формы траектории, работа силы в потенциальном силовом поле по замкнутой траектории равна нулю.
Можно показать, что необходимым и достаточным условием того, что силовое поле является потенциальным, является условие 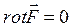
Непотенциальными являются силы сопротивления, зависящие от скорости и силы трения. Сила сухого трения скольжения не будет потенциальной, так как хотя она постоянна и не зависит от скорости, но направление силы трения от скорости зависит.
Наряду с силовой функцией можно ввести другую функцию, характеризующую запас энергии в данной точке поля – потенциальную энергию.
Потенциальной энергиейПматериальной точки в рассматриваемой точке силового поля M называют работу, которую совершают силы поля, действующие на материальную точку при перемещении ее из положения M в начальное положение M0:
Постоянная С0 одна и та же для всех точек поля, зависящая от того, какая точка поля была выбрана за начало отсчета.
В конечном итоге имеем: 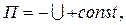
Потенциальное силовое поле
3.3.5.1. Потенциальное силовое поле и силовая функция
Силовое поле – это часть пространства, в каждой точке которого на материальную точку действует сила, зависящая от координат точки и времени (рис. 3.27)
Силовое поле называют стационарным, если силы не зависят явно от времени 

Силовое поле называют потенциальным если имеется силовая функция 
Рассмотрим основные свойства силовой функции стационарного поля.
1. Из определения следует, что силовая функция определена с точностью до постоянной
2. Элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции. Это свойство силовой функции можно принять за ее определение. Элементарная работа:
т.е.
3. Полная работа силы на каком–либо перемещении точки равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой совершается это перемещение, если силовая функция является однозначной (рис. 3.28). Полная работа силы 

4. Из предыдущего свойства следует, что работа силы в потенциальном силовом поле по любому замкнутому контуру равна нулю, так как значения силовой функции в начальной и конечной точках перемещения одинаковы:
5. Силу 

Определены условия, которые позволяют по силам силового поля установить, будет ли силовое поле потенциальным. Эти условия имеют вид:
Силы, действующие на материальную точку в потенциальном поле, называются потенциальными. К ним относят: силы тяжести, линейную силу упругости, силу тяготения.
Для механической системы в потенциальном силовом поле силовая функция является функцией координат всех точек системы
Проекция силы, действующей на каждую точку системы, будет равна
Если вычислить сумму работ, которую совершают силы поля, действующие на механическую систему при перемещении из положения (M0), в котором силовая функция равна U0, в положение (М), в котором силовая функция равна U, то получим
3.3.5.2. Потенциальная энергия
В случае потенциального силового поля вводят функцию, характеризующую запас энергии в данной точке поля – потенциальную энергию материальной точки в рассматриваемой точке силового поля.
Потенциальной энергией П материальной точки в рассматриваемой точке потенциального силового поля М (рис. 3.29) называют работу, которую совершают силы поля, действующие на материальную точку при перемещении ее из точки М в начальную точку M0:


Потенциальная энергия определена с точностью до постоянной
Проекции силы на координатные оси имеют вид:
Элементарная и полная работа силы в потенциальном силовом поле:
Потенциальной энергией системы P в рассматриваемом положении (М) потенциального силового поля называют сумму работ сил поля, действующих на систему, которую эти силы совершают при перемещении системы из рассматриваемого положения в начальное положение (M0):
где U – значение силовой функции в положении (М); U0 – значение силовой функции в начальном положении (M0).
Проекции силы, действующей на каждую точку системы, на координатные оси имеют вид:
Элементарная и полная работа сил поля:
3.3.5.3. Закон сохранения механической энергии
Закон сохранения механической энергии точки. Для материальной точки, согласно теореме об изменении кинетической энергии, справедливо уравнение
Если точка движется в стационарном потенциальном силовом поле, то

Обозначая через Е полную механическую энергию точки, получаем
Закон сохранения механической энергии для точки. При движении точки в стационарном потенциальном силовом поле ее полная механическая энергия остается постоянной величиной.
Закон сохранения механической энергии системы. Теорему об изменении кинетической энергии для системы можно представить в виде
При движении системы в стационарном потенциальном силовом поле:
где П – потенциальная энергия внутренних и внешних сил, действующих на систему. Следовательно,

Последняя формула выражает закон сохранения механической энергии для системы.
Закон сохранения механической энергии для системы. Полная механическая энергия при движении системы в стационарном потенциальном силовом поле внешних и внутренних сил является величиной постоянной.
Механические системы, для которых выполняется закон сохранения механической энергии, называются консервативными.
Потенциальное поле сил



Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения части
Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными (сила трения). Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части: 1а2 и 2b1. Так как поле
 |
| Рис. 5.5. Работа в потенциальном поле сил |
потенциально, то, по условию 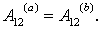
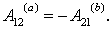
что и требовалось доказать.
Наоборот, если работа сил поля на любом замкнутом пути равна нулю, то и работа этих сил на пути между произвольными точками 1 и 2 от формы пути не зависит, т. е. поле потенциально. Для доказательства выберем два произвольных пути: 1а2 и 1b2 (рис. 5.5). Составим из них замкнутый путь 1a2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. 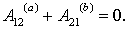
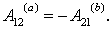
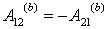
Введем понятие потенциальной энергии частицы в поле. То, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.
Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек P в фиксированную точку O. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки P (при фиксированной точке O ). А это значит, что данная работа будет некоторой функцией радиус-вектора r точки P.
Обозначив эту функцию 
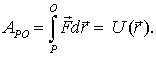 | (5.9) |
Функцию 
Ранее было показано, что при перемещении частицы из одной точки потенциального поля в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы, т. е. 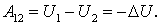
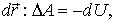
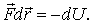 | (5.14) |
Учитывая, что 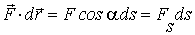
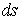
где 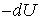
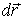
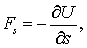 | (5.15) |
Перемещение 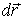
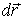
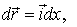
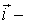
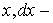
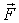
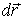
где 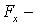
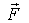
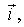
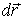
Подставив последнее выражение в уравнение (5.14), получим
где символ частной производной означает, что потенциальная энергия 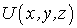
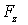
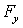
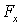
Итак, взяв с обратными знаками частные производные функции U по х, у и z, мы найдем проекции 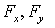
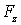
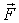

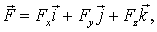
Величину, стоящую в скобках, называют градиентом (полным дифференциалом) скалярной функции U и обозначают 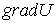

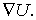
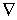
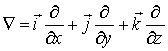
Т.о., сила, действующая на точку со стороны силового поля, выража-
ется через градиент потенциальной энергии точки в этом поле, взятый
с обратным знаком. Т.е. сила оказывается направленной в сторону наи-
быстрейшего убывания потенциальной энергии.
7.Нормировка потенциальной энергии.
Потенциальная энергия принимается равной нулю для некоторой конфигурации (координат) тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии. 
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
| |
|
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
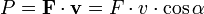 |
F — сила, v — скорость, α — угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
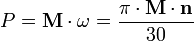 |
M — момент силы, 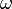
2. Энергия системы материальных точек.
Кинетическая энергия системы.
Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы
Кинетическая энергия является характеристикой и поступательного и вращательного движения системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:
Кинетическая энергия – скалярная и всегда положительная величина.
Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.
1. Поступательное движение.
В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки
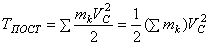
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит.
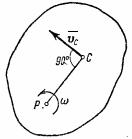
2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рис.46), то скорость любой его точки 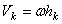
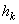
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:
т. е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.
При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.47)
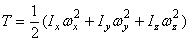
где Ix, Iy, Iz – моменты инерции тела относительно главных осей инерции x1, y1, z1 в неподвижной точке О ; 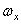
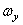
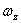
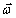









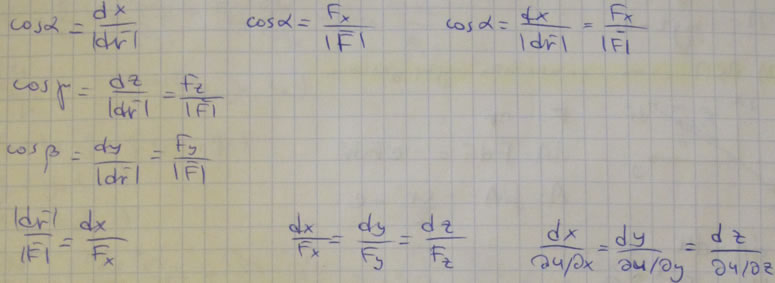
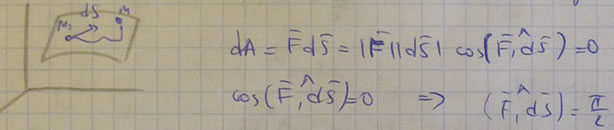
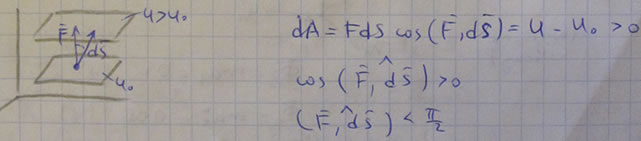



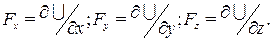
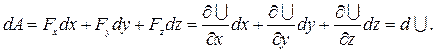
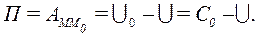



























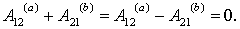


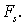
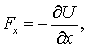
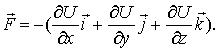

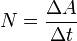 — средняя мощность
— средняя мощность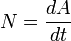 — мгновенная мощность
— мгновенная мощность