Что такое посылка логика
Силлогизм: фигуры и модусы, правила терминов
Силлогизм — первостепенная фигура таких дисциплин, как философия и логика. Он используется в логике для формулирования понятий, суждений и умозаключений. Однако не стоит думать, что сфера применения данного понятия специфична и ограничивается наукой. Осведомленность в этой области позволит взрослому человеку емко и грамотно формулировать мысли, в ускоренном темпе продвигаться по карьерной лестнице и не позволить коллеге себя обмануть.
В рамках данной статьи постараемся объяснить простыми словами, что это такое – силлогизм, какие рассуждения называют силлогизмами, что считается фигурами и модусами простого категорического силлогизма.
Определение понятия
Силлогизм – это правильный вывод, сделанный индивидом на основе сведений, которыми он располагает. Это новая истина, родившаяся из двух исходных умозаключений. Случается, что подсказанные товарищем или лежащие на поверхности утверждения оказываются правильными только на первый взгляд. При детальном же изучении и анализе вскрывается их ошибочность.
Главный закон любого рассуждения отражен в его аксиоме: правомерность перехода к заключению от посылок объясняется следующими моментами:
Понятие логических модусов
В структуре простого силлогизма выделяются модусы. Модусы силлогизма являются его фигурами. Модусы (фигуры) силлогизма определяются законами логики и разновидностью силлогизма. Модусы простого категорического силлогизма состоят из следующих элементов: большой термин (Р), средний термин (М), меньший термин (S). Можно сказать, что большой термин – это сказуемое, а меньший термин силлогизма, который используется в заключении, является его субъектом. Простой категорический силлогизм не предполагает использование среднего термина в заключении.
В определении фигур используются следующие правильные модусы простого категорического силлогизма:
А – все субъекты являются первичными тезисами;
I – некоторые субъекты являются первичными тезисами;
Е – все субъекты не являются первичными тезисами;
О – некоторые субъекты не являются первичными тезисами.
В категорическом силлогизме эти фигуры складываются в 11 правильных сочетаний: ААА, ААI, АЕЕ, АЕО, АII, АОО, ЕАЕ, ЕАО, ЕIО, IAI, ОАО. Все остальные сочетания приведут к ошибкам.
В зависимости от расположения среднего термина, структура будет изменяться.
Первая фигура (подчинительная):
Все демоны страшные.
Некоторые силы зла – демоны.
Некоторые силы зла страшные.
Вторая фигура (юридическая):
Все ангелы – не демоны.
Некоторые силы зла – демоны.
Некоторые силы зла страшные.
Третья фигура (опровергающая):
Все демоны страшные.
Некоторые демоны – силы зла.
Некоторые силы зла страшные.
Все ангелы – не демоны.
Некоторые демоны – силы зла.
Некоторые силы зла страшные.
Во всех этих примерах средним термином являются демоны, большим – ангелы, меньшим – силы зла.
Примеры фигур отражают разные задачи логики. Правила фигур определяются назначением суждения. Первая фигура энтимемы используется для показа применения общих положений теории к ее частным моментам. Вторая фигура отвергает ложное подчинение. Третья фигура энтимемы используется для доказательства того, что из любого правила бывают исключения. Четвертая фигура – это модус в философии, а не в логике.
Интересно, что понятие модуса часто используется в интеллектуальных заданиях. Их можно встретить в журналах и газетах. Например, в сканвордах нужно подобрать слово из 5 букв, обозначающее разновидность силлогизма.
Правила построения суждений
При построении любого простого силлогизма имеет смысл соблюдать правила во избежание казусов и курьезов. Правильный простой категорический силлогизм соответствует всем требованиям терминов и посылок.
Правила терминов
В логике правилами терминов силлогизма являются:
Простым примером нарушения этого правила терминов является следующее умозаключение:
Законопроекты не разрабатываются людьми.
Закон – это документ государства.
Законопроекты, существующие в государстве, не создают люди.
Если сказать простыми словами, то ошибка возникла потому, что был введен лишний термин – «закон». Вместо 3 их стало 4.
Проиллюстрировать эту ошибку можно элементарным примером:
Планеты обладают отраженным светом.
Луна обладает отраженным светом.
Луна – планета.
Однако луна – это не планета. Ошибка возникла из-за нераспределенности среднего термина.
Мне кажется, что изъяснить это правило можно на следующем примере:
Человек болен, если у него повышенная температура тела.
У девушки нет повышенной температуры тела.
Девушка не больна.
Вывод ложный, так как медицине известны болезни, при которых температура тела не повышается.
Правила терминов распространяются априори на все энтимемы.
Правила посылок
Разновидности и модусы силлогизма должны соответствовать правилам посылок, по которым определяется правильность фигуры умозаключения:
Приведем пример ошибки посылки умозаключения:
Некоторые города в нашей стране – столицы республик бывшего СССР.
Некоторые населенные пункты Архангельской области являются городами нашей страны.
Некоторые города Архангельской области – столицы республик бывшего СССР.
Правила посылок определяют его истинность или ложность.
Классификация рассуждений
В логике и философии выделяют простые и сложные виды силлогизмов. Приведем примеры популярных видов умозаключений.
Простой категорический тип
Простой категорический силлогизм – это утвердительное умозаключение. Термины простого категорического силлогизма называются истинными посылками. Правила простого категорического силлогизма позволяют выделить следующие фигуры этого вида умозаключения:
Модусы простого категорического силлогизма зависят от количественных и качественных параметров посылок и итоговых суждений. В логике этот вид насчитывает 19 модусов. Становится понятно, что такое умозаключение, как простой категорический силлогизм, – это ключевая фигура логики и философии. Чаще всего простой категорический силлогизм состоит из сочетания типа ААА.
Условино-категорический тип
Простыми словами можно сказать, что к этому виду относятся такие примеры суждений, где одна посылка содержит условное суждение, а вторая – категорическое. Становится очевидным, что независимо от меньшего термина, итог такого силлогизма может быть как утвердительным, так и отрицательным. При этом финал такого рассуждения всегда верный.
Что же такое модус простого категорического силлогизма? Это такое суждение, в котором:
Примером рассуждения этого типа будет следующее умозаключение:
Небесные тела способны к движению.
Все планеты – это небесные тела.
Все планеты способны к движению.
Разделительный тип
Что такое разделительный силлогизм? Определение этого вида умозаключений строится на разделительных посылках, из которых получается разделительное итоговое суждение (количество альтернатив при этом увеличивается).
Разделительный логический силлогизм может иметь в структуре одно разделительное суждение-посылку и одно категорическое суждение-посылку.
Итоговое суждение в этом случае может быть либо отрицательно-утверждающим, либо утверждающе-отрицательным.
Условно-разделительный тип
Условно-разделительное суждение – это умозаключение, в котором одна из посылок включает разделительное суждение, а вторая содержит несколько условных рассуждений. Прогрессивная наука положила схему этого силлогизма в основу леммы, дилеммы и полилеммы.
Непосредственный тип
Непосредственное умозаключение – это вывод, который можно вывести из единственной посылки посредством ее превращения, обращения или противопоставления чему-либо. Сама посылка при этом изменяется, приобретая противоположное значение. Простым примером такого типа рассуждений будет следующее умозаключение:
Пирамиды не бывают плоскими.
Любая пирамида – объемная фигура.
Сложные формы силлогизмов
Кроме простых разновидностей умозаключений существуют сложные типы. Сложным видом умозаключения называется утверждающе-сложный силлогизм. В логике такие формы умозаключений называют полисиллогизмами. Например:
Все звезды являются небесными телами.
Солнце – это звезда.
Солнце является небесным телом.
Все небесные тела способны к движению.
Солнце способно к движению.
Ложный силлогизм
Ложный тип рассуждения – это ошибочное умозаключение, которое основано на ложных посылках. В нем нарушаются правила логики: используют нераспределенные термины, излишнее количество посылок или терминов. Говорят, что формулирование ложных выводов – это особенность женского логического мышления.
Способы проверки истинности рассуждения
Для того, чтобы определить, является ли рассуждение правильным, его подвергают тщательному анализу:
Рекомендуется использовать такие способы проверки истинности конечного суждения, как:
Заключение
Силлогизмы – это не просто один из терминов логики. Они нужны в каждой отрасли науки для того, чтобы сопоставлять факты, формулировать умозаключения, делать выводы на основе имеющихся данных. Понятия, суждения и умозаключения являются неотъемлемым компонентом познания.
В современном мире ценятся люди, обладающие рациональным мышлением, умеющие конструировать гипотезы, доказывать их и делать верные выводы при анализе информации. На собеседованиях в престижных фирмах специалисты по подбору персонала и менеджеры по кадрам часто задают соискателю вопросы, направленные на оценку умений человека мысленно составить грамотные логические конструкции.
10. Краткий курс логики. Умозаключение
Умозаключение – это форма мышления, в которой из двух суждений, называемых посылками, вытекает третье – вывод.
1. Посылка: «Все люди – смертны».
2. Посылка: «Сократ – человек»
Ввод: «Сократ – смертный».
Умозаключения бывают непосредственные и опосредованные. Непосредственные умозаключения делаются из одной посылки, и являют собой уже известные нам действия над суждениями (обращения, превращения, противоставления предикату), а так же преобразование суждений по логическому квадрату. Опосредованные умозаключения делаются из нескольких посылок, о них мы и будем говорить в данной главе.
Существуют такие виды опосредованных умозаключений, их еще называют методами мышления:
Дедуктивный метод (Силлогизм) – метод при котором вывод о частном делается из общей совокупности вещей, о которых говориться в посылках. Проще говоря – вывод от общего к частному. К примеру:
1 посылка: «В группе 311 все студенты отличники».
2 посылка: «Этот ученик из 311 группы»
Вывод: «Этот ученик – отличник».
Еще пример:
1 посылка: «В этом ящике все шарики красные»
2 посылка: «Этот шарик их этого ящика»
Вывод: «Этот шарик красный».
Преимущество дедуктивного метода заключается в том, что при правильном использовании всегда дает точные выводы. Важно понимать, что все посылки входящие в силлогизм должны быть истинными, ложность хотя бы одной из них, ведет к ложности вывода. В принципе кто знаком с произведениями Артура Конана Дойля, должен был слышать о дедуктивном способе мышления. Его использовал Шерлок Холмс, в одном из произведений он приводит пример своего дедуктивного умозаключения Ватсону. Около жертвы преступления было найдена выкуренная сигарета, все решили, что сигарету выкурил полковник перед смертью. Однако у покойного были большие пышные усы, а сигарета была докуренная полностью. Шерлок Холм берется доказывать, что полковник не мог курить эту сигарету, так как он непременно бы подпалил бы себе усы. Вывод дедуктивный и верный, так как из общего правила вытекает частное.
Общее правило и первая посылка, выглядит так: «Все люди, которые носят большие, пышные усы не могут выкурить сигарету до конца»
Событие или вторая посылка выглядит так: «Полковник носил большие, пышные усы».
Вывод: «Полковник не мог выкурить сигарету до конца»
Индукция – метод, при котором вывод об общем делается из совокупности частных случаев. Проще говоря – это вывод от частного к общему. И пример тому:
1 посылка: «Первый, второй и третий студент – отличники».
2 посылка: «Эти студенты из 311 группы».
Вывод: «Все студенты в 311 группе – отличники».
1 посылка: ««Этот шарик красный».
2 посылка: «Этот шарик их этого ящика».
Вывод: «В этом ящике все шарики красные»
Некоторые учебники различают полную и не полную индукцию, полная индукция это когда перечисляются все элементы конечного множества вещей, о котором рассуждают. В нашем примере берутся все ученики и проверяют отличники они все или нет, а уже потом заключают обо всей группе. Не полная или частичная индукция – это наши примеры, в которых берутся только некоторые элементы конечного множества вещей. Само собой разумеется, не полное индуктивное заключения, на отмену от дедуктивного носит вероятностный, а не достоверный характер. Тем не менее, это не мешает пользоваться этим методом умозаключения в повседневной жизни. К примеру, мы, я уверен, слышали такое высказывание из уст женщины «Все мужчины – козлы», а ведь вывод об общем сделан из частного, по всем правилам индуктивного мышления.
1 посылка: «Первый человек – козел»
2 посылка: «Второй человек – козел».
3 посылка: «Эти люди – мужчины»
Вывод: «Все мужчины – козлы».
Чаще всего не полные индуктивные выводы – неверные. Их преимущество состоит в том, что они направленны на расширения знаний о предмете, могут указать на новые их свойства, в то время как индуктивный метод чаще всего направлен на выяснения уже известных фактов.
Я с некоторыми другими логиками выделяю еще такой вид умозаключения как Абдукция. Абдукция – это вид умозаключения, при котором на основе общего, делается вывод о причине частного, проще говоря – это вывод от общего к причине частного.
Я считаю, на отмену от общепринятого мнения, что именно этот вид умозаключений использовал на самом деле Шерлок Холмс, а так же другие реальные и не реальные детективы.
Чтобы понять, в чем заключается суть Абдукции, ее лучше рассматривать в сравнении с другими видами умозаключения.
А: «В этом ящике все шарики красные»
Б: «Этот шарик их этого ящика»
В: «Этот шарик красный».
Как видим с помощью дедукции – мы узнали результат, теперь переделаем рассуждения под индукцию:
Б: «Этот шарик их этого ящика»
В: «Этот шарик красный».
А: «В этом ящике все шарики красные»
Индукция, вывод от частного к общему открыл нам правило. Не трудно догадаться, что должен быть еще один вид умозаключений, который открывал бы нам случай, причину, ним и является Абдукция. Такой вид умозаключений будет выглядит так:
Существует, еще такой вид умозаключений как «вывод по аналогии». Это когда на основе свойств, признаков одного предмета делается вывод о свойствах другого. Формально это выглядит так:
Предмет А имеет свойство а, б, с, д.
Предмет В имеет свойсво а, б, с.
Вероятно В имеет и свойство д.
Так же как и неполная индукция умозаключения по аналогии носит вероятностный характер, но, не смотря на это, он широко используется, как в повседневной жизни, так и в науке.
Вернемся к дедукции. Мы предположили, что дедуктивный вид умозаключения имеет достоверный характер. Но, тем не менее, надо выделить некоторые правила простого силлогизм, чтобы это было действительно так. Итак, рассмотрим общие правила силлогизма.
1. В силлогизме должно быть только три термина или не должно быть термина, который употребляется в двух значениях. Если такой есть считается, что в силлогизме больше трех терминов, так как четвертый подразумевается. К примеру:
Движение – вечно.
Хождение в университет – это движение.
Хождение в университет – вечно.
Термин «Движение» употреблено в двух смыслах, в первом суждении, первой посылке оно обозначает всеобщее мировое изменения. А во второй механическое передвижение из одной точки в другую.
2. Средний термин должен быть распределён хотя бы в одной из посылок. Средний термин – это термин, который является базисом рассуждения и находиться в каждой из посылок.
Все хищные животные (+) – живые существа (-)
Все хомяки (+) – живые существа (-).
Все хомяки – хищные животные.
Средним термином является «живые существа». В обоих посылках его объем не распределён. В первой посылке оно не распределено, потому, что живые существа – это не только хищные животные. А во втором, потому, что живые существа – это не только все хомяки. Соответственно вывод в данном суждении не верный.
Еще один пример, который недавно прочел в одном журнале:
Все старые фильмы (+) – черно белые (-)
Все пингвины (+) – черно белые (-).
Пингвины – это старые фильмы.
Средний термин, то есть термин, который встречается в двух посылках – «черно белый». Как в первом, так и во втором суждении он не распределён, ведь черно белыми могут быть не только все старые фильмы или все пингвины.
4. Посылки силлогизма не могут быть только отрицательными. Вывод в таком силлогизме в лучшем случае будет вероятностным, но чаще всего его либо вообще невозможно сделать, либо он ложен.
5.Посылки силлогизма не могут быть только частными. Хотя бы одна посылка из силлогизма должна быть общая. В силлогизме, в котором две посылки частные сделать вывод не возможно.
6.Если в силлогизме одна посылка отрицательная, то и вывод будет отрицательным.
7.Если в силлогизме одна посылка частная, вывод из него следует так же только частный.
Силлогизм – самый распространённый вид умозаключений, потому, мы часто используем его в повседневной жизни и науке. Однако мы редко соблюдаем его логическую форму, и пользуемся сокращенными силлогизмами. К примеру: «Сократ смертный, потому, что все люди смертные». «Этот шарик красный, потому, что его взяли из ящика, в котором все шарики красные». «Железо – электропроводно, так как все металлы электропроводны» и т.д.
Различают такие виды сокращенного силлогизма:
Энтимема – это сокращенный силлогизм, в котором пропущена одна из посылок или вывод. Понятно, что из простого силлогизма можно вывести три энтимемы. К примеру, из простого силлогизма:
Все металлы – электропроводные.
Железо – это метал.
Железо – электропроводно.
Можно вывести три энтимемы:
1. «Железо – электропроводно так как оно является металлом». (пропущена первая посылка)
2. «Железо – электропроводно потому, что все металлы электропроводны». (пропущена вторая посылка)
3. «Все металлы электропроводны, а железо тоже метал». (пропущен вывод)
Следующий вид сокращенного умозаключения – Эпихейрема. Оно являет собой простой силлогизм, в которой две посылки – энтимемы.
Сначала сделаем из двух силлогизмов энтимемы:
Силлогизм №1.
Все то, что ограничивает человеческую свободу, делает его рабом.
Социальная необходимость ограничивает человеческую свободу
Социальная необходимость делает человека рабом.
Первая энтимема, если пропустить первую посылку будет выгладить так:
«Социальная необходимость делает человека рабом, потому, что ограничивает человеческую свободу.
Силлогизм №2.
Все действия, которые дают возможность существовать в социуме – являются социальной необходимостью.
Работа – это действие, которое дает возможность существовать в социуме.
Работа – это социальная необходимость.
Вторая энтимема, если пропустить первую посылку: «Работа – это социальная необходимость, так как является действием, которое дает возможность существовать в социуме».
Теперь сделаем силлогизм из двух энтимем, который и будет нашей эпихейремой:
Социальная необходимость делает человека рабом, потому, что ограничивает человеческую свободу.
Работа – это социальная необходимость, так как является действием, которое дает возможность существовать в социуме.
Работа – делает человека рабом.
Не исключено, что именно в таком порядке рассуждал Ницше говоря: «Мы видим, к чему сводится жизнь в обществе — каждый отдельный индивид приносится в жертву и служит орудием. Пройдите по улице, и вы увидите только «рабов». Куда? Зачем?»
Сорит – полисиллогизм, в котором пропущено суждение, связывающее два простых силлогизма, то есть вывод первого силлогизма, который стал первой посылкой второго, попросту упускается.
Все что развивает память и мышления – полезно.
Изучения наук – развивает память и мышления.
Логика – это наука.
Изучения логики – полезно.
Как видим суть силлогизма от того, что оно из полисиллогизма превратилось в сорит, не поменялась.
Посылка (логика)
Аристотель утверждал, что любой логический аргумент может быть сведен к двум посылкам и выводу. Посылки иногда опускают, в этом случае они называются опущенными посылками, например:
Сократ смертен, так как все люди смертны.
Очевидно, что Сократ является человеком (эта посылка опущена). Развернутым суждением было бы:
Так как все люди смертны, а Сократ — человек, то следовательно Сократ смертен.
В этом примере два первых независимых высказывания — «все люди смертны» и «Сократ — человек» — это посылки, в то время как «Сократ смертен» является выводом.
Доказательство вывода зависит как от истинности обеих посылок, так и от обоснованности аргумента.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Деду́кция (лат. deductio — выведение, также дедуктивное умозаключение, силлогизм) — метод мышления, следствием которого является логический вывод, в котором частное заключение выводится из общего. Цепь умозаключений (рассуждений), где звенья (высказывания) связаны между собой логическими выводами.
На эту страницу установлено перенаправление со страницы «A posteriori», см. также статью о музыкальном альбоме «A Posteriori».Апостерио́ри, а постерио́ри (лат. a posteriori букв. «из последующего») — знание, полученное из опыта. Противопоставляется априори — доопытному знанию. Значение термина исторически менялось: нынешнее значение установилось благодаря И. Канту и его работе «Критика чистого разума» (впервые опубликована в 1781 году, второе издание в 1787 г.) Однако, в латинской форме, выражения.
Инду́кция (лат. inductio — наведение, от лат. inducere — влечь за собой, установить) — процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не строго через законы логики, а скорее через некоторые фактические, психологические или математические представления.Объективным основанием индуктивного умозаключения является всеобщая связь явлений в природе.
Урок 7. Силлогизмы

Содержание:
Простой категорический силлогизм
Простой категорический силлогизм – это одно из наиболее простых и часто встречающихся умозаключений. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует отношение между терминами А и С.
В данном случае, термин «рыбы» – это общий термин для двух посылок, и он помогает связать термины «акулы» и «существа, способные жить без воды». Общий термин для двух посылок принято называть средним термином. Субъект заключения (в нашем примере это «акулы») называют меньшим термином. Предикат заключения («существа, способные жить без воды») называют бóльшим термином. Соответственно, посылку, содержащую меньший термин, называют меньшей посылкой («Все акулы – это рыбы»), а посылку, содержащую больший термин, – бóльшей посылкой («Все рыбы не могут жить без воды»).
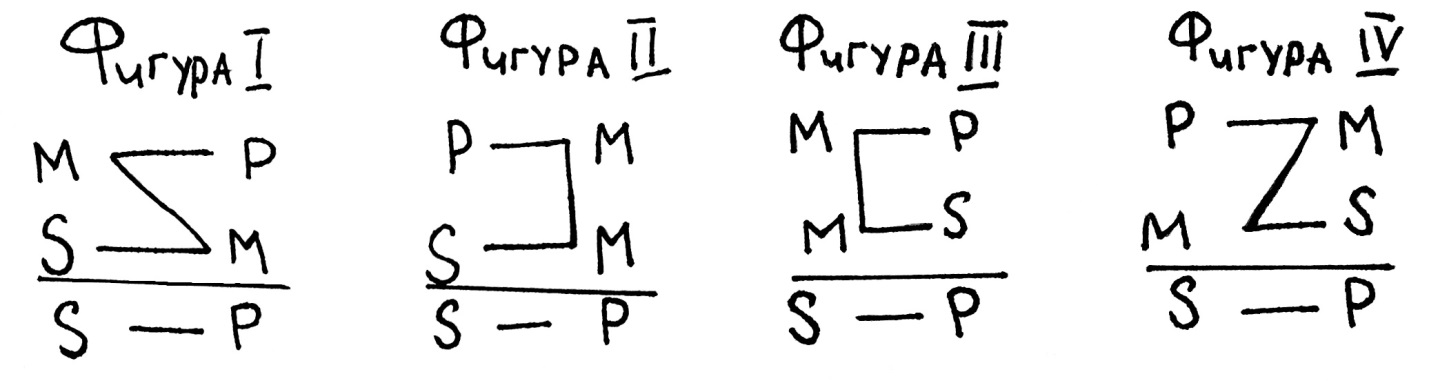
Естественно, в рассуждении посылки могут находиться в любой последовательности. Однако для удобства проверки правильности силлогизмов, большую посылку ставят всегда первой, а меньшую – второй. Тогда в зависимости от расположения терминов все простые категорические силлогизмы можно разделить на четыре вида. Эти виды называются фигурами.
Фигура – это форма простого категорического силлогизма, которая определяется расположением среднего термина.
Сверху расположена большая посылка, за ней следует меньшая посылка, под чертой находится заключение. Буквой S обозначен меньший термин, буквой P – больший термин, буквой М – средний термин.
Далее, фигуры могут наполняться разным содержанием, то есть на место посылок и заключений могут подставляться разные типы категорических атрибутивных высказываний. Например:
Эти различные сочетания высказываний в фигурах образуют так называемые модусы. Каждая фигура имеет 64 модуса, таким образом, на все четыре фигуры приходятся всего 256 модусов. Если подумать обо всём многообразии умозаключений, имеющих форму силлогизмов, то 256 модусов – это не так уж и много. Кроме того, далеко не все модусы образуют правильные умозаключения, то есть существуют такие модусы, которые при истинности посылок не гарантируют истинности умозаключения. Такие модусы называются неправильными. Правильными же называются те модусы, с помощью которых из истинных посылок мы всегда получаем истинное заключение. Всего существует 24 правильных модуса – по шесть на каждую фигуру. Это означает, что во всей классической силлогистике, которая исчерпывает львиную долю рассуждений, производимых людьми, существует всего 24 вида правильных умозаключений. Это очень маленькое число, поэтому правильные модусы не так уж и сложно запомнить.
Каждый из этих модусов ещё в Средние века получил особое мнемоническое наименование. Каждый тип категорического атрибутивного высказывания был обозначен с помощью всего одной буквы. Высказывания типа «Все S есть P» обозначили буквой «а», первой буквой в латинском слове «affirmo» («утверждаю»), и их запись превратилась в «SaP». Высказывания вида «Некоторые S есть P» записывались с помощью буквы «i», второй гласной в слове «affirmо», поэтому они выглядели как «SiP». Высказывания формы «Ни один S не есть P» обозначили буквой «е», первой гласной в латинском слове «nego» («отрицаю»), их стали записывать в виде «SeP». Как вы, наверное, уже догадались высказывания типа «Некоторые S не есть P» обозначили буквой «о», второй гласной в слове «nego», их формальная запись выглядела как «SoP». Поэтому модусы правильных силлогизмов традиционно обозначаются именно с помощью этих четырёх букв, которые для удобства запоминания представлены в виде слов. Таблица всех правильных модусов выглядит так:
К примеру, модус второй фигуры Cesare (eae) в развёрнутом виде будет выглядеть так:
Хотя 24 модуса – это совсем не много и в таблице можно усмотреть некоторые регулярности (например, для всех фигур верны модусы eao и eio), запомнить её всё равно сложно. К счастью, это совсем и необязательно. Для проверки силлогизмов можно также пользоваться модельными схемами. Только в отличие от тех схем, которые мы строили раньше, на них уже должно присутствовать не два, а три термина: S, P, M.
Давайте возьмём модус четвёртой фигуры Bramantip (aai) и проверим его с помощью модельных схем.
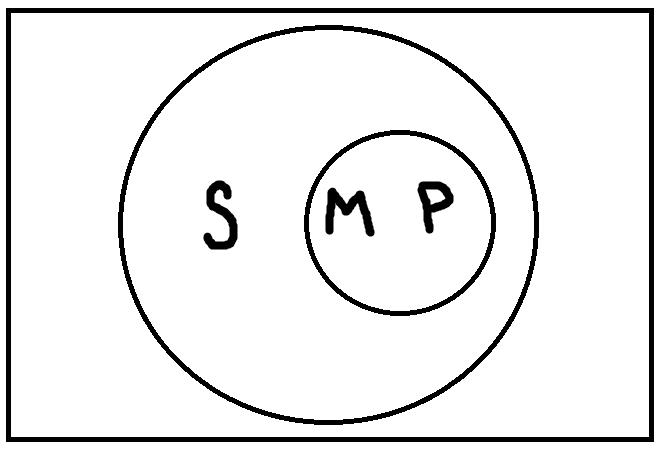
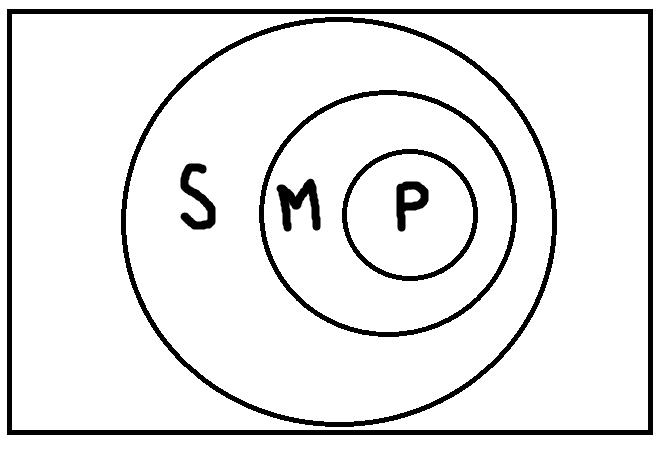
Сначала нужно найти такие модельные схемы, при которых обе посылки будут одновременно истинными. Таких схем всего четыре:
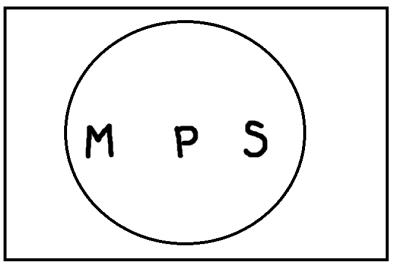
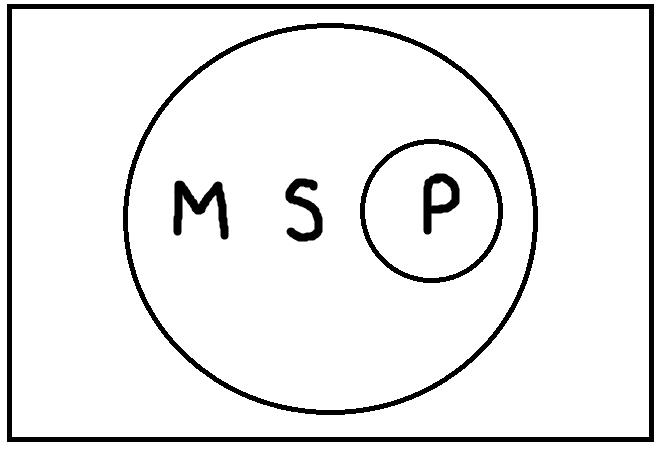
Теперь на каждой из этих схем мы должны проверить, верно ли будет высказывание «Некоторые S есть P», представляющее заключение. В результате проверки, мы обнаруживаем, что на каждой схеме это высказывание будет верным. Таким образом, умозаключение по модусу Bramantip (aai) четвёртой фигуры правильное. Если бы была хотя бы одна схема, на которой это высказывание было бы ложным, то умозаключение было бы неправильным.
Метод проверки силлогизмов с помощью модельных схем хорош, так как он позволяет представить отношения между терминами наглядно. Однако для некоторых посылок могут оказаться верными очень много схем сразу. В результате их построение и проверка будут представлять собой трудоёмкую и отнимающую много времени задачу. Таким образом, метод модельных схем не всегда удобен.
Поэтому логики разработали ещё один метод для определения, правильный силлогизм или нет. Этот метод называется синтаксическим и представляет собой два перечня правил (правила терминов и правила посылок), при соблюдении которых силлогизм будет верным.
Модус простого категорического силлогизма является правильным, если он удовлетворяет следующим условиям:
Правила терминов
Правила посылок понятны, а правила терминов требуют некоторых пояснений. Начнём с правила о трёх терминах. Хотя оно кажется очевидным, оно довольно часто нарушается вследствие так называемой подмены терминов. Посмотрите на следующий силлогизм:
Прежде всего, если вы помните фигуры и правильные модусы, вы сразу можете сказать, что этот силлогизм неправильный, так как он относится ко второй фигуре и имеет модус aaa, который не принадлежит к списку правильных модусов для этой фигуры. Но если вы их не помните, всё равно вы можете выявить его ложность, потому что здесь явно присутствует четыре термина, вместо трёх. Термин «золото» употребляется в двух совершенно различных смыслах: как химический элемент и как нечто, обладающее ценностью. Посмотрим на более сложный пример:
Кажется, что этот силлогизм соответствует модусу Barbara первой фигуры. Однако посылки истинны, а заключение ложно. Проблема в том, что в этом примере опять произошло учетверение терминов. Вроде бы этот силлогизм содержит три термина. Меньший термин – «”Отцы и дети” Ивана Тургенева». Больший термин – «книги, которые нельзя прочитать за целую жизнь». Средний термин – «книги из собрания Российской государственной библиотеки». Если же присмотреться внимательно, то станет ясно, что субъектом первой посылки является не термин «книги из собрания Российской государственной библиотеки», а термин «все книги из собрания Российской государственной библиотеки». В данном случае «все» – это не квантор общности, а часть субъекта, так как это слово употребляется не в разделительном смысле (каждый в отдельности), а в собирательном (все вместе). Если бы мы заменили слово «все» на слова «каждый в отдельности», то первая посылка попросту стала бы ложной: «Каждую в отдельности книгу из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь». Таким образом, мы получаем четыре термина вместо трёх, а потому это умозаключение ложно.
Теперь перейдём к правилам о распределённости терминов. Для начала объясним, что это за характеристика. Термин называют распределённым, если в высказывании речь идёт обо всех объектах, входящих в его объём. Соответственно, термин не распределён, если в высказывании речь идёт не обо всех объектах, составляющих его объём. Грубо говоря, термин распределён, если мы говорим обо всех предметах, и не распределён, если мы говорим только о некоторых предметах, о части объёма термина.
Давайте возьмём типы высказываний и посмотрим, какие термины в них распределены, а какие нет. Распределённый термин отмечается знаком «+», нераспределённый – знаком «–».
Как видно, субъект всегда распределён в общих и единичных высказываниях, но не распределён в частных. Предикат всегда распределён в отрицательных высказываниях, но не распределён в утвердительных. Если теперь перенести это на наши правила для терминов, то получается, что средний термин хотя бы в одной из посылок должен быть взят во всём своём объёме.
Хотя и высказывания над чертой и высказывание под чертой истинны, умозаключение как таковое здесь отсутствует. Здесь нет логического перехода от посылок к заключению. И это можно легко выявить, так как средний термин «птицы» ни разу не берётся во всём своём объёме.
Что касается третьего правила терминов, если в посылках речь идёт только о части объектов из объёма терминов, то в заключении мы не можем ничего утверждать обо всех объектах объёма терминов. Мы не может перейти от части к целому. Кстати, обратный переход возможен: если мы говорим обо всех элементах объёма терминов, то мы можем сделать заключение о части из них.
Энтимемы
Во время реальных дискуссий и споров мы довольно часто опускаем те или иные части рассуждения. Это приводит к возникновению энтимем. Энтимема – это сокращённая форма умозаключения, в которой пропущены посылки или заключение. Важно не путать энтимемы с однопосылочными умозаключениями. Энтимема – это именно многопосылочное умозаключение, просто его части в силу тех или иных причин опущены. Иногда такие пропуски оправданы, так как оба собеседника хорошо разбираются в проблеме, и им нет нужды проговаривать все шаги. Между тем, недобросовестные собеседники могут специально пользоваться энтимемами, чтобы затемнить и запутать своё рассуждение и скрыть свои истинные аргументы или выводы. Поэтому необходимо уметь отличать корректные энтимемы от некорректных. Энтимема называется корректной, если она может быть восстановлена в виде правильного модуса категорического силлогизма, и если все пропущенные посылки оказываются истинными.
Поговорим о том, как восстановить энтимему до полного силлогизма. В первую очередь нужно понять, что именно пропущено. Для этого нужно обратить внимание на слова-маркеры, обозначающие причинно-следственные связи: «таким образом», «следовательно», «так как», «потому что», «в результате» и т.д. К примеру, возьмём рассуждение: «Золото – это драгоценный металл, потому что оно практически не окисляется на воздухе». Здесь заключением является высказывание «Золото – это драгоценный металл». Одна из посылок: «Золото практически не окисляется на воздухе». Ещё одна посылка пропущена. Нужно сказать, что чаще всего пропускают именно одну из посылок. Довольно странно, если в рассуждении отсутствует самое важное – вывод.
Итак, мы установили, что именно пропущено. В нашем примере – это посылка. Большая это посылка или меньшая? Как вы помните, меньшая посылка содержит субъект заключения («золото»), а большая – предикат заключения («драгоценный металл»). Посылка, содержащая субъект заключения нам уже известна: «Золото практически не окисляется на воздухе». Значит, нам известна меньшая посылка, и не известна большая. Кроме того, благодаря известной посылке, мы можем установить и средний термин: «металлы, которые практически не окисляются на воздухе», – тот термин, который не содержится в заключении.
Теперь располагаем известную нам информацию в форме силлогизма:
В большей посылке должны находиться предикат заключения и средний термин: «драгоценные металлы» (P) и «металлы, которые окисляются на воздухе» (M). Здесь возможны два варианта:
Значит, возможен силлогизм либо второй фигуры, либо первой фигуры. Теперь смотрим на нашу табличку с правильными модусами силлогизмов. Во второй фигуре вообще нет правильных модусов, где в заключении стояло бы высказывание типа а. В первой фигуре есть только один такой модус – Barbara. Достраиваем наш силлогизм:
Теперь проверяем, истинна ли наша восстановленная посылка. В нашем случае она истинна, поэтому энтимема была правильной.
Сориты
Термином «сориты» пользовался Льюис Кэррол для обозначения сложных силлогизмов, которые имеют более чем две посылки. По большому счёту, сорит представляет собой гибрид силлогизма и энтимемы. Он устроен следующим образом: дано множество посылок, из каждой пары посылок делаются промежуточные выводы, которые обычно опускаются, к промежуточным выводам присоединяются новые посылки, из них делаются новые промежуточные выводы, к которым опять присоединяются новые посылки и так далее, пока мы не переберём все имеющиеся посылки и не дойдём до окончательного заключения. В принципе подобным образом люди и рассуждают в повседневной жизни. Поэтому очень важно уметь решать сориты и оценивать, правильны они или нет.
Мы приведём пример сорита из книги Льюиса Кэррола «История с узелками»:
1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Человек с длинными волосами не может не быть поэтом.
3. Амос Джадд никогда не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. В этой округе нет других поэтов, кроме полисменов.
6. С нашей кухаркой не ужинает никто, кроме её кузенов.
7. Все люди с короткими волосами сидели в тюрьме.
8. Амос Джадд любит холодную баранину.
Над чертой находятся посылки, под чертой – заключение.
Как же нужно решать и проверять сориты? Дадим пошаговую инструкцию. Во-первых, необходимо привести все посылки в более или менее стандартную форму:
1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Все люди с длинными волосами являются поэтами.
3. Амос Джадд не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. Все поэты из нашего округа являются полисменами.
6. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
7. Все люди с короткими волосами сидели в тюрьме.
Теперь нужно взять две исходные посылки. По большому счёту, неважно, с каких именно посылок вы начнёте. Главное, чтобы ваши исходные посылки вместе содержали всего три термина. Это означает, что мы не можем взять посылки «Амос Джадд не сидел в тюрьме» и «Все кузены нашей кухарки любят холодную баранину». В них входят четыре разных термина, а потому мы не можем сделать из них никакого заключения. Я в качестве исходных возьму посылки 7 и 3 и сделаю из них вывод по правилам для простых категорических силлогизмов.
Этот силлогизм соответствует модусу Camestres (aee) второй фигуры. Теперь для удобства я переформулирую наш промежуточный вывод следующим образом: «Амос Джадд является человеком с длинными волосами». Этот промежуточный вывод я соединяю с посылкой номер 2:
Этот силлогизм соответствует модусу Barbara (aaa) первой фигуры. Теперь я присоединяю этот промежуточный вывод к посылке номер 5:
Этот силлогизм опять же соответствует модусу Barbara (aaa) первой фигуры. Присоединяем промежуточный вывод к посылке номер 1:
Это силлогизм, как вы уже, наверное, заметили, тоже представляет собой модус Barbara (aaa) первой фигуры. Присоединяем этот вывод к посылке номер 6:
Опять Barbara, которая является одним из самых распространённых модусов. Присоединяем к нашему последнему промежуточному выводу последнюю посылку номер 4:
Итак, с помощью всё того же модуса Barbara мы получили наше заключение: «Амос Джадд любит холодную баранину». Таким образом, сориты решаются и проверяются с помощью пошагового разделения на простые категорические силлогизмы. В нашем примере сорит оказался правильным, но возможны и обратные ситуации. Существует два условия корректности соритов. Во-первых, каждый сорит должен разбиваться на последовательность правильных модусов силлогизмов. Во-вторых, заключение, которое вы получаете, когда все посылки исчерпаны, должно совпасть с заключением сорита. Это условие действует в тех случаях, когда вы имеете дело с чужим рассуждением, в котором уже присутствует какое-то заключение.
Итак, мы рассмотрели различные многопосылочные умозаключения на примере простых категорических силлогизмов, энтимем и соритов. По большому счёту, если вы знаете, как иметь с ними дело, то вы вооружены для любых дискуссий с любыми противниками. Единственное, что может на данный момент вызывать некоторое недовольство, это необходимость тратить много времени на проверку правильности умозаключений. Не стоит расстраиваться по этому поводу: лучше выглядеть тугодумом, который рассуждает правильно, чем блестящим демагогом, который не замечает своих и чужих ошибок. Тем более, с накоплением опыта внимательного отношения к умозаключениям у вас появится чутьё, автоматический навык, позволяющий быстро отделять корректные рассуждения от некорректных. Поэтому упражнений к этому уроку будет много, чтобы у вас была возможность набить руку.
Задачи Эйнштейна
Эта игра является нашей версией всемирно известной «загадки Эйнштейна», в которой 5 иностранцев живут на 5 улицах, едят 5 видов еды и т.д. Подробнее про эту задачу написано здесь. В подобных заданиях вам нужно сделать правильное умозаключение на основе имеющихся посылок, которых, на первый взгляд, для этого недостаточно.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Упражнения
Упражнения 1, 2 и 3 взяты из книги Льюиса Кэррола «История с узелками», М.: Мир, 1973.
Упражнение 1
Сделайте заключения из следующих посылок по правилам для простого категорического силлогизма. Помните, что простой категорический силлогизм должен содержать только три термина. Не забывайте приводить высказывания к стандартному виду.
Упражнение 2
Проверьте, правильны ли следующие рассуждения. Попробуйте разные способы проверки. Не забывайте ставить большую посылку на первую строку.
Упражнение 3
Найдите заключения следующих соритов.
Упражнение 4
Проверьте правильность следующих энтимем.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.