Что такое постоянное ускорение

Что такое постоянное ускорение

В общем случае движение может быть криволинейным и неравномерным.
Тогда вектор скорости будет меняться и по направлению, и по величине, а это значит, что тело движется с ускорением.
Ускорение показывает быстроту изменения скорости.

Единица измерения ускорения в системе СИ:

Прямолинейное движение с постоянным ускорением подразделяется на:
1. равноускоренное, когда при движении модуль скорости тела увеличивается (тело разгоняется).
Здесь векторы скорости и ускорения совпадают по направлению.

2. равнозамедленное, когда при движении модуль скорости тела уменьшается (тело тормозит).
Здесь векторы скорости и ускорения направлены противоположно друг другу.

Формула ускорения:
1. в векторном виде

2. расчетная формула в координатной форме (для решения задач)

Отсюда «вытекает» уравнение скорости, которое выражает мгновенную скорость тела в любой момент времени:
1. в векторном виде

2. расчетная формула в координатной форме

Графики ускорения

Перемещение

1. формула перемещения в векторном виде

2. Расчетная формула в координатной форме

Графики перемещения

Уравнение движения (или иначе уравнение координаты)

1. в векторном виде

2. расчетная формула в координатной форме

Примеры решения задач на движение с постоянным ускорением

Задача 1

Решение

Сравниваем заданное уравнение движения х=2-4t-2t 2 с формулой:

По полученным данным даем описание движения тела:

Составляем уравнение скорости, глядя на расчетную формулу для скорости:

Расчитываем скорость и координату тела через 10 секунд после начала движения:

Задача 2

Уравнение движения тела x=-3+t+t 2
Дать описание движения тела.
Определить скорость и координату тела через 2 секунды после начала движения.

Решение

Рассуждаем аналогично вышерассмотренной задаче:

Источник

Движение тела с постоянным ускорением

Всего получено оценок: 275.

Всего получено оценок: 275.

Одним из частых видов неравномерного движения является движение тела с постоянным ускорением. Рассмотрим особенности такого движения, выведем его кинематическую формулу.

Ускорение

Самым простым видом движения является равномерное и прямолинейное. Однако, большинство движений являются равномерными и прямолинейными лишь на некотором участке пути. Трение и взаимодействия с другими телами приводят к тому, что большая часть движений происходят с изменением скорости, то есть неравномерно. Покоящееся тело имеет нулевую скорость, потом начинает движение, и его скорость увеличивается, а после равномерного участка происходит замедление и остановка, скорость тела опять изменяется.

При этом, поскольку скорость – это векторная величина, то даже при постоянном модуле она может меняться, изменяя направление.

Изменение скорости может происходить с разной быстротой. Одна и та же скорость может быть достигнута с нулевой за различное время. Для оценки этой быстроты используется специальный параметр – ускорение.

Ускорение равно отношению изменения скорости движения ко времени этого изменения:

Ускорение – это векторная величина, если движение с ускорением происходит не по прямой, а на плоскости или в пространстве, ее направление и модуль находятся по правилам действий с векторами.

Из формулы ускорения следует, что единицей ускорения является метр в секунду за секунду или метр в секунду в квадрате.

Рис. 1. Ускорение в физике.

Скорость движения при постоянном ускорении

Движение с постоянным ускорением называется равноускоренным, независимо от того, увеличивает ли тело скорость или уменьшает. Хорошим примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха не играет роли. Еще Галилей установил, что все тела при падении увеличивают скорость одинаково, то есть движутся с равным ускорением.

$$\overrightarrow v = \overrightarrow v_0 + \overrightarrow at$$

Это основная формула скорости при равноускоренном движении.

Рис. 2. Пример графика скорости равноускоренного движения.

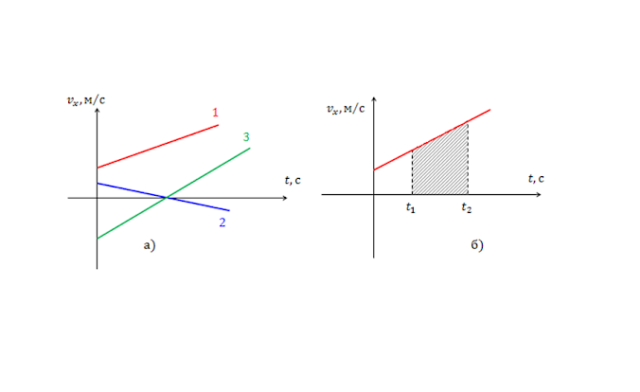
Перемещение при равноускоренном движении

Из графика скорости можно определить перемещение, учитывая, что величина перемещения равна площади фигуры под графиком.

$$\overrightarrow x =\overrightarrow x_0+\overrightarrow v_0t+<\overrightarrow at^2\over 2>$$

Это основная формула перемещения при равноускоренном движении. Отметим, что она представляет собой уравнение второй степени, то есть график перемещения при равноускоренном движении будет параболой.

Рис. 3. Пример графика перемещения равноускоренного движения.

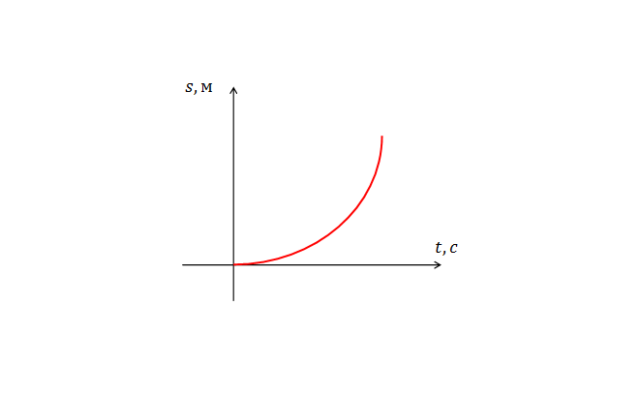
Обе приведенных формулы связывают скорость и перемещение материальной токи с моментом времени. Но, при решении задач иногда требуется, чтобы формула напрямую связывала скорость и перемещение. Выразив время из формулы скорости, и подставив его в формулу расстояния, получим:

Заметим, что данное соотношение имеет скалярный вид. Так происходит из-за присутствия действий умножения и деления, которые не применимы к векторным величинам, поэтому последнюю формулу можно использовать лишь только после проецирования векторов на оси координат.

Что мы узнали?

Ускорение – это величина, характеризующая быстроту изменения скорости движения. Если при движении ускорение не меняется, такое движение называется равноускоренным. График скорости при равноускоренном движении представляет собой наклонную прямую, график перемещения – параболу.

Источник

Ускорение при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

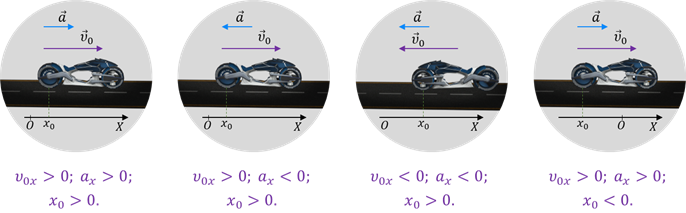
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

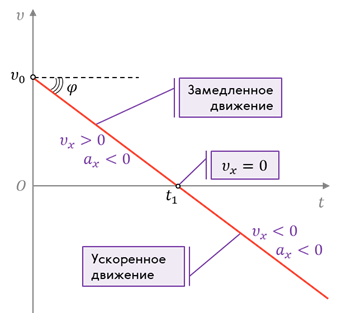
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Ускорение. Уравнение движения точки с постоянным ускорением

Урок 5. Физика 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Ускорение. Уравнение движения точки с постоянным ускорением»

Мы с вами изучили равномерное прямолинейное движение, то есть движение, при котором точка за любые равные промежутки времени совершает одинаковые перемещения. Но, как мы уже отмечали, при реальном движении тел их скорости обычно меняются или по модулю, или по направлению, или же одновременно и по модулю, и по направлению. Например, когда автомобиль трогается с места, его скорость постепенно возрастает. А при торможении на перекрёстке, наоборот, — уменьшается.

При вращательном движении скорость любой точки дисков электрофорной машины изменяется лишь по направлению (конечно же, при условии, что число оборотов в единицу времени не изменяется).

Наконец, при выстреле из пушки под некоторым углом к горизонту скорость ядра будет изменяться как по модулю, так и по направлению.

При этом очевидно, что в рассмотренных нами примерах изменение скорости может происходит как очень быстро, так и достаточно медленно.

Физическая векторная величина, характеризующая быстроту изменения скорости, называется ускорением.

Давайте вспомним, как определяется ускорение точки. Для этого рассмотрим её неравномерное движение вдоль некоторой криволинейной траектории. Пусть в некоторый момент времени t она занимает положение М и имеет скорость υ. А спустя некоторый промежуток времени Δt₁ — положение М₁ и скорость υ₁.

Найдём изменение скорости точки за это время как геометрическую разность векторов конечной и начальной скоростей и укажем эту разность на рисунке:

Если теперь мы с вами разделим вектор изменения скорости на промежуток времени, в течение которого это изменение произошло, то тем самым получим так называемый вектор среднего ускорения точки:

Он направлен точно так же, как и вектор изменения скорости.

Но как же нам определить ускорение точки в положении М? Для этого будем уменьшать рассматриваемые промежутки времени и находить вектор изменения скорости для каждого случая. Из полученного рисунка видим, что вектор изменения скорости, а следовательно, и вектор среднего ускорения, уменьшается по модулю и при этом меняется его направление. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости точки за это время. Следовательно, при стремлении промежутка времени к нулю отношение будет стремиться к своему некоторому предельному значению.

Физическая векторная величина, равная пределу отношения изменения скорости к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенным ускорением (или просто ускорением):

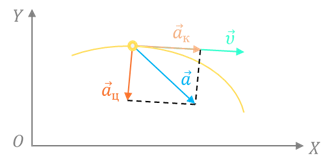
Важно запомнить, что вектор ускорения направлен так же, как и вектор изменения скорости при стремлении промежутка времени к нулю. И в общем случае вектор ускорения не совпадает с направлением вектора скорости, а составляет с ним некоторый угол.

Как мы уже видели, при неравномерном движении по криволинейной траектории скорость точки непрерывно меняется по модулю и направлению. Поэтому вектор ускорения часто называют полным ускорением и представляют в виде суммы двух ускорений:

Первое ускорение называется тангенциальным (или касательным), так как направлено оно по касательной к траектории движения. Его модуль характеризует изменение модуля скорости:

Второе ускорение всегда направлено перпендикулярно вектору мгновенной скорости и поэтому называется нормальным (нормаль — это перпендикуляр) или центростремительным. Его модуль характеризует изменение скорости по направлению:

А вектор центростремительного ускорения в любой момент времени направлен к центру кривизны траектории.

Конечно же движение точки может происходить как с постоянным, так и с переменным ускорением. Так, если отношение изменения скорости к промежутку времени в течение которого это изменение произошло одинаково для любого интервала времени, то говорят, что точка движется с постоянным ускорением. А движение точки называют равноускоренным движением:

Из формулы видно, что если скорость и промежуток времени выражены в единицах СИ, то единицей измерения ускорения является метр на секунду в квадрате (м/с 2 ).

Также из формулы следует, что за единицу ускорения в СИ принимается ускорение такого равноускоренного движения, при котором за 1 с скорость точки изменяется на 1 м/с.

Теперь давайте выясним, как зависит скорость точки от времени при её равноускоренном движении. Итак, пусть в начальный момент времени t₀ скорость точки равнялась , а в момент времени t — .

Тогда ускорение точки равно изменению вектора скорости к промежутку времени, за который это изменение произошло:

Если начальный момент времени принять равным нулю, то из этого уравнения легко получить формулу для определения скорости точки в любой момент времени при её равноускоренном движении — уравнение скорости:

Таким образом, чтобы определить скорость точки в произвольный момент времени, необходимо знать её начальную скорость и ускорение.

На практике при вычислениях скорости мы будем пользоваться формулами, в которые входят не векторы, а их проекции на соответствующие координатные оси:

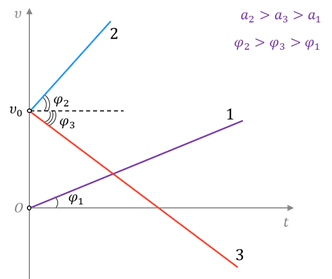
Из записанных формул видно, что при равноускоренном движении скорость точки линейно зависит от времени. Значит, график скорости представляет собой прямую линию, наклонённую к оси времени под некоторым углом. При этом чем больше ускорение точки, тем больший угол с осью времени составляет график проекции скорости.

Теперь посмотрим на прямую 3. Что можно сказать о движении тела в этом случае?

Во-первых, очевидно, что за промежуток времени от нуля до t₁ проекция скорости была положительна.

Во-вторых, скорость точки уменьшалась и в момент времени, равный t₁ она стала равной нулю. Точка пересечения графика скорости с осью времени называется точкой поворота. В ней направление скорости меняется на противоположное, после чего тело начинает двигаться равноускоренно.

Теперь давайте вспомним, что основной задачей механики является определение положения точки в любой момент времени. Получим уравнения, которые позволяют это сделать для равноускоренного движения. Для примера рассмотрим случай, когда проекция начальной скорости и ускорения положительны. По аналогии со случаем равномерного прямолинейного движения логично предположить, что проекция перемещения, совершённого телом за время t, будет равна площади фигуры, ограниченной графиком, осью времени и перпендикуляром, восставленным к графику из точки t. В данном случае эта фигура — трапеция.

Для доказательства этого предположения рассмотрим очень малый промежуток времени Δt внутри выбранного интервала времени. По аналогии с мгновенной скоростью, если выбранный промежуток времени достаточно мал, то изменением скорости за это время можно пренебречь. То есть движение точки можно считать равномерным. Значит, проекция перемещения за это время будет равна площади этого маленького прямоугольника. При этом очевидно, что на такие узкие полоски мы можем разбить всю площадь фигуры под графиком скорости

Тогда, согласно рисунку, проекция перемещения при равноускоренном движении определяется площадью трапеции. Площадь же трапеции, как известно из геометрии, равна произведению полусуммы её оснований на высоту. В нашем случае длина одного из оснований численно равна проекции начальной скорости точки, второго — проекции скорости через время t. Высота же трапеции численно равна времени.

Теперь вспомним, что по определению проекция перемещения численно равна разности конечной и начальной координат точки:

Тогда после небольших математических преобразований получим формулу для определения координаты точки при её равноускоренном движении:

Важно помнить, что в формулу входят проекции начальной скорости и ускорения точки. А они могут быть как положительными, так и отрицательными. Координата начального положения точки также может быть больше или меньше нуля,

Если движение точки происходит в пространстве, то для определения оставшихся двух координат используют уравнения, имеющие аналогичной вид:

Записанные нами формулы называются кинематическими уравнениями движения точки в координатной форме. Они применимы для описания как прямолинейного, так и криволинейного движения.

В общем виде кинематические уравнения движения можно записать с помощью одного векторного уравнения:

Теперь для закрепления материала решим с вами одну небольшую задачку. Итак, на рисунке представлен график зависимости скорости точки от времени. Определите, в какой момент времени координата точки станет равной 30 м, если в момент начала наблюдения её координата равнялась –6 м. Определите скорость точки в этот момент времени.

Источник