Что такое постоянная функция
Какие свойства элементарных функций?
Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.
Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.
Постоянная функция
Выделяют следующие виды основных элементарных функций:
Постоянная функция определяется формулой: y=C (C – некое действительное число) и имеет также название: константа. Данная функция определяет соответствие любому действительному значению независимой переменной x одного и того же значения переменной y – значение C.
График константы – это прямая, которая параллельна оси абсцисс и проходит через точку, имеющую координаты (0, С). Для наглядности приведем графики постоянных функций y=5, y=-2, y=3, y=3 (на чертеже обозначено черным, красным и синим цветами соответственно).
Свойства постоянных функций:
Корень n-й степени
Данная элементарная функция определяется формулой y=xn (n – натуральное число больше единицы).
Рассмотрим две вариации функции.
Корень n-й степени, n – четное число
Похожий вид у графиков функции четной степени при иных значениях показателя.
Свойства функции корень n-ой степени, n – четное число
Такая функция определена на всем множестве действительных чисел. Для наглядности рассмотрим графики функций y=x3, y=x5 и x9. На чертеже они обозначены цветами: черный, красный и синий цвета кривых соответственно.
Иные нечетные значения показателя корня функции y=xn дадут график аналогичного вида.
Свойства функции корень n-ой степени, n – нечетное число
Степенная функция
Степенная функция определяется формулой y=xa. Вид графиков и свойства функции зависят от значения показателя степени.
Область определения функции
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Область определения степенной функции
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
Рассмотрим несколько примеров.
Область определения показательной функции
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Свойства постоянной функции.
I. Теоретическая часть.
1. Функция. Определения и свойства.
Число а называют угловым коэффициентом прямой, он равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. Графиком линейной функции является прямая линия. Она определяется двумя точками.
Свойства линейной функции
3. Функция принимает нулевое значение при 

4. Функция возрастает (убывает) на всей области определения.
5. Линейная функция непрерывная на всей области определения, дифференцируемая и 
Квадратичная функция.
Коэффициенты а, b, с определяют расположение графика на координатной плоскости
Свойства функции:
2. Множество значений одного из промежутков: 
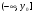
3. Функция принимает нулевые значения при 

4. Функция непрерывна на всей области определения и производная функции равна 
Показательная функция.
Функция вида 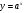

Свойства функции:
2. Е(у)= 
3. Функция возрастает (а>1), убывает (а 0.
Примеры степенных функций: 
Коэффициент b определяет положение графика на координатной плоскости.
1. Функция определена для х>0.
2. Е(у)= 
3. Функция возрастающая, если b>0 и убывающая, если b 2 + bx + c называют квадратичной. Графиком квадратичной функции является кривая, называемая параболой. Точку с координатами 
1) множество X (которое называется областью определения функции);2) множество Y (которое называется областью значений функции);3) закон соответствия (который иногда называется функциональной зависимостью).
При этом закон соответствия может быть задан любым способом: таблицей, графиком, формулой или как-то иначе, например, при помощи словесного описания. Если функцию задают формулой, то при этом фактически указывают область определения функции и закон соответствия (область значений функции не указывается явно, так как она устанавливается исходя из данной формулы).Областью определения функции, заданной явной аналитической формулой, считают множество всех тех значений аргумента, для которых все указанные в формуле операции выполнимы.
способы построения графиков функций.
1. Способ «по точкам». Вытекает из определения графика функции. Он является длинным и недостаточно надежным. Применяется в школьном курсе математики при первоначальном знакомстве с простейшими функциями.
2. Способ «путем сдвига графиков основных функций или сдвига осей координат». Чтобы построить график функции y = f (x) + c можно или график функции y = f (x) сдвинуть вдоль оси 0y на c единиц в сторону, совпадающую со знаком c, или перенести параллельно ось 0y в сторону, противоположную знаку c. Чтобы построить график функции y = f (x + b), можно или график функции y = f (x) вдоль оси 0x на b единиц в сторону, противоположную знаку b, или перенести параллельно ось 0y в сторону, совпадающую со знаком b.
4. Способ «путем деформирования графиков основных функций». Чтобы построить график функции y = af (x) при a > 0, можно график исходной функции растянуть (сжать) вдоль оси ординат, если a > 1 (0 0, можно график исходной функции растянуть (сжать) вдоль оси абсцисс, еслиb > 1 (0 [1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.
Число 


В случае, если у числовой последовательности существует предел в виде вещественного числа 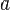
Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.
Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.
Можно дать альтернативные определения предела последовательности. Например, называть пределом число, в любой окрестности которого содержится бесконечно много элементов последовательности, в то время, как вне таких окрестностей содержится лишь конечное число элементов. Таким образом, пределом последовательности может быть только предельная точка множества её элементов. Это определение согласуется с общим определением предела для топологических пространств.
Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании. Всё это выводится из доказываемых ниже свойств предела.
5. Предел функции в точке и в бесконечности.
Рассмотрим функцию 
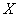

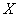





Существуют два определения Предела функции в точке.
Число 

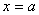
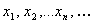





Для обозначения предельного значения функции используется следующая символика: 
Отметим, что функция 


Рассмотрим несколько Примеров.
1. Функция 






2. Функция 




Соответствующие последовательности значений функций для них:

Таким образом, Определение 1 не удовлетворяется, так как для двух разных последовательностей значений аргумента, сходящихся к нулю, соответствующие последовательности значений функции имеют разные пределы.
6. Бесконечно малые функции и их свойства.
Если 


Свойства
1. Сумма (разность) конечного числа бесконечно малых функций при 
Доказательство
Пусть 




что влечет за собой условия

Если 
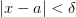
2. Произведение бесконечно малой функции 


Доказательство
Так как функция 


существует число

Так как функция 



и

Выберем 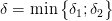
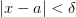
Следовательно
3. Произведение конечного числа бесконечно малых функций при 
Доказательство
Так как любая бесконечно малая функция 



7. Основные теоремы о пределах функции.
Определение. Число A называетсяпределом функции y = f(x) в точке x0(иногда говорят, при x, стремящемся кx0), если для любого положительного числа e можно найти такое положительное число d, что для всех xиз d—окрестности точки x0соответствующие значения y попадают в e—окрестность точки y = A.
Можно сформулировать определение предела функции по-другому.
Определение. Число A называетсяпределом функции y = f(x) в точке x0, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию 0 2 – 4ac

















