Что такое порядок уравнений
Дифференциальные уравнения для «чайников». Примеры решения
Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.
Основные понятия теории дифференциальных уравнений
Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.
Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.
Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.
Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.
Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.
Решение уравнений
Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.
Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:
Решить такое уравнение можно, просто проинтегрировав его правую часть.
Примеры таких уравнений:
Уравнения с разделяющимися переменными
В общем виде этот тип уравнений выглядит так:
Решая такое уравнение, нужно разделить переменные, приведя его к виду:
После этого останется проинтегрировать обе части и получить решение.
Математика
Линейные дифференциальные уравнения первого порядка
Такие уравнения имеют вид:
Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:
Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).
Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.
Пример решения ДУ с разделяющимися переменными
Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.
Сначала перепишем производную в более привычном виде:
Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:
Теперь осталось проинтегрировать обе части:
Интегрируем и получаем общее решение данного уравнения:
Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Порядок дифференциального уравнения и его решения, задача Коши
Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков.
Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём.
Кроме обыкновенных изучаются также дифференциальные уравнения с частными производными. Это уравнения, связывающие независимые переменные 
, неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные».
Примеры дифференциальных уравнений:
(1) 
;
(2) 
;
(3) 
;
(4) 
;
(5) 
.
Дифференциальное уравнение n-го порядка не обязательно должно содержать явно функцию, все её производные от первого до n-го порядка и независимую переменную. В нём могут не содержаться явно производные некоторых порядков, функция, независимая переменная.
Решением дифференциального уравнения называется всякая функция y = f(x), при подстановке которой в уравнение оно обращается в тождество.
Процесс нахождения решения дифференциального уравнения называется его интегрированием.
Пример 1. Найти решение дифференциального уравнения 
.
Решение. Запишем данное уравнение в виде 
. Решение состоит в нахождении функции по её производной. Изначальная функция, как известно из интегрального исчисления, есть первообразная для 
, т. е.
.
Это и есть решение данного дифференциального уравнения. Меняя в нём C, будем получать различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка.
Общим решением дифференциального уравнения n-го порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е.
Решение дифференциального уравнения в примере 1 является общим.
Частным решением дифференциального уравнения называется такое его решение, в котором произвольным постоянным придаются конкретные числовые значения.
Пример 2. Найти общее решение дифференциального уравнения 
и частное решение при 
.
Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения.
,
,
.
данного дифференциального уравнения третьего порядка.
Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов их значения и получим
.
Если кроме дифференциального уравнения задано начальное условие в виде 
, то такая задача называется задачей Коши. В общее решение уравнения подставляют значения 
и 
и находят значение произвольной постоянной C, а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.
Пример 3. Решить задачу Коши для дифференциального уравнения из примера 1 при условии 
.
Решение. Подставим в общее решение значения из начального условия y = 3, x = 1. Получаем
.
Записываем решение задачи Коши для данного дифференциального уравнения первого порядка:
.
При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования и взятия производных, в том числе сложных функций. Это видно на следующем примере.
Пример 4. Найти общее решение дифференциального уравнения 
.
Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части.
.
Применяем метод интегрирования заменой переменной (подстановкой). Пусть 
, тогда 
.
Возвращаясь к переменной x, получаем:
.
Это и есть общее решение данного дифференциального уравнения первой степени.
Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть независимой переменной, то есть, переменной x. Помогут решить эту проблему не забытые (впрочем, у кого как) со школьной скамьи знания о пропорции. Таков следующий пример.
Пример 5. Найти общее решение дифференциального уравнения 
.
Решение. Как видим, переменная x в уравнении отсутствует. Вспоминаем из курса дифференциального исчисления, что производная может быть записана также в виде 
. В результате уравнение приобретает вид
,
то есть, в нём в некотором виде появился x.
Теперь вспомнаем одно из свойств пропорции: из пропорции 
выткают следующие пропорции:
,
то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
Применяя это свойство, преобразуем уравнение к виду
,
после чего интегрируем обе части уравнения:
.
и получаем решение данного дифференциалного уравнения первого порядка:
.
Эта статья представила необходимый минимум сведений о дифференциальных уравнениях и их решениях и должна помочь вам уверенно и увлечённо перейти к изучению различных видов дифференциальных уравнений.
Что такое порядок уравнений
уЙНЧПМЙЮЕУЛЙ ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ НПЦОП ОБРЙУБФШ ФБЛ
.
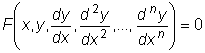
рПТСДЛПН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС ОБЪЩЧБЕФУС РПТСДПЛ ОБЙЧЩУЫЕК РТПЙЪЧПДОПК, ЧИПДСЭЕК Ч ХТБЧОЕОЙЕ.
оБРТЙНЕТ, ХТБЧОЕОЙЕ
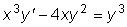
ЕУФШ ХТБЧОЕОЙЕ РЕТЧПЗП РПТСДЛБ, Б ХТБЧОЕОЙЕ
— ХТБЧОЕОЙЕ ЧФПТПЗП РПТСДЛБ.
тЕЫЕОЙЕН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС ОБЪЩЧБЕФУС ЧУСЛБС ЖХОЛГЙС y(x), ЛПФПТБС ВХДХЮЙ РПДУФБЧМЕООПК Ч ХТБЧОЕОЙЕ, ПВТБЭБЕФ ЕЗП Ч ФПЦДЕУФЧП. тЕЫЕОЙЕ ЕЭЕ ОБЪЩЧБЕФУС ЙОФЕЗТБМПН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС.
рТЙНЕТ
тБУУНПФТЙН ХТБЧОЕОЙЕ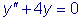 
.
жХОЛГЙС 
СЧМСЕФУС ТЕЫЕОЙЕН ЬФПЗП ХТБЧОЕОЙС.
дЕКУФЧЙФЕМШОП,
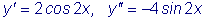
Й ХТБЧОЕОЙЕ ПВТБЭБЕФУС Ч ФПЦДЕУФЧП: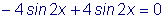 
.
тЕЫЕОЙЕН ТБУУНБФТЙЧБЕНПЗП ХТБЧОЕОЙС ВХДХФ Й ЖХОЛГЙЙ
Й ЧППВЭЕ ЖХОЛГЙЙ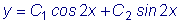 
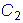
, ЗДЕ 
Й 
— РТПЙЪЧПМШОЩЕ РПУФПСООЩЕ.
ч УБНПН ДЕМЕ
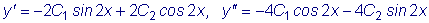
Й ХТБЧОЕОЙЕ ПВТБЭБЕФУС Ч ФПЦДЕУФЧП 
.
ъБНЕФЙН, ЮФП ТБУУНБФТЙЧБЕНПЕ ХТБЧОЕОЙЕ ЙНЕЕФ ВЕУЮЙУМЕООПЕ НОПЦЕУФЧП ТЕЫЕОЙК ЧЙДБ: .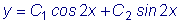
тЕЫЕОЙЕ ДЙЖЖЕТЕОГЙБМШОЩИ ХТБЧОЕОЙК РЕТЧПЗП РПТСДЛБ
дЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ РЕТЧПЗП РПТСДЛБ ЙНЕЕФ ЧЙД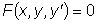 
.
пВЭЕЕ Й ЮБУФОПЕ ТЕЫЕОЙЕ
рТЙНЕТ
тБУУНПФТЙН ХТБЧОЕОЙЕ
.
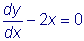
пВЭЙН ТЕЫЕОЙЕН ЬФПЗП ХТБЧОЕОЙС СЧМСЕФУС УЕНЕКУФЧП ЖХОЛГЙК
.
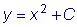
дЕКУФЧЙФЕМШОП, РТЙ МАВПН ЪОБЮЕОЙЙ C ЬФБ ЖХОЛГЙС ХДПЧМЕФЧПТСЕФ ХТБЧОЕОЙА: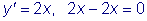 
.
лТПНЕ ФПЗП, ЧУЕЗДБ НПЦОП ОБКФЙ ФБЛПЕ ЪОБЮЕОЙЕ C, ЮФП УППФЧЕФУФЧХАЭЕЕ ЮБУФОПЕ ТЕЫЕОЙЕ ВХДЕФ ХДПЧМЕФЧПТСФШ ЪБДБООПНХ ОБЮБМШОПНХ ХУМПЧЙА.
ьФП ТЕЫЕОЙЕ НПЦОП РПМХЮЙФШ, ЙУРПМШЪХС ОЙЦЕРТЙЧЕДЕООЩК БРРМЕФ ДМС РПУФТПЕОЙС РПМС ОБРТБЧМЕОЙК Й ЙОФЕЗТБМШОЩИ ЛТЙЧЩИ ДМС ХТБЧОЕОЙС РЕТЧПЗП РПТСДЛБ.
тЕЫЙФШ ЙМЙ РТПЙОФЕЗТЙТПЧБФШ ДБООПЕ ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ ЬФП ЪОБЮЙФ:
Б) ОБКФЙ ЕЗП ПВЭЕЕ ТЕЫЕОЙЕ ЙМЙ ПВЭЙК ЙОФЕЗТБМ, ЕУМЙ ОЕ ЪБДБОЩ ОБЮБМШОЩЕ ХУМПЧЙС,
В) ОБКФЙ ЮБУФОПЕ ТЕЫЕОЙЕ, ХДПЧМЕФЧПТСАЭЕЕ ЪБДБООЩН ОБЮБМШОЩН ХУМПЧЙСН.
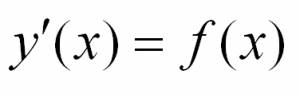
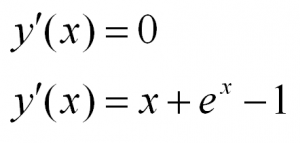
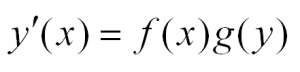
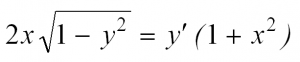
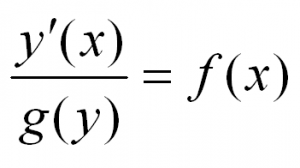
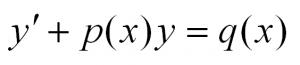
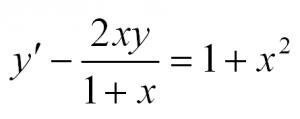
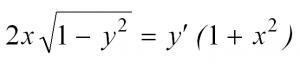
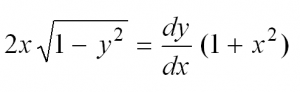
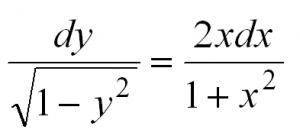
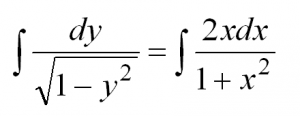
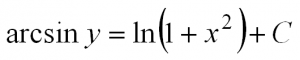
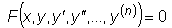
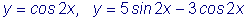
(7.1)
. (7.4)
имеет решениями функции y = Cx, а дифференциальное уравнение 
— функции 
где C — произвольное число.
имеет общее решение y = Cx. Зададим начальное условие 
. Подставим эти значения в общее решение, получим 6 = 2С, откуда С = 3. Следовательно, функция y = 3x удовлетворяет и дифференциальное уравнение, и начальное условие.
.
имеет общее решение y = Cx, то ему соответствует семья прямых, 
имеет общее решение, ему соответствует семья равносторонних гипербол (рис. 2). 
то это означает, что задана точка M0 (x0;y0), через которую должна проходить интегральная кривая, отвечающая искомому частному решению. Таким образом, отыскание частного решения дифференциального уравнения по заданному начальному условию геометрически означает, что из семьи 
.
, удовлетворяющее начальному условию 
— это общее решение дифференциального уравнения. 
является частным решением данного уравнения.
.
.
— общий интеграл дифференциального уравнения.
откуда 
будем иметь: 
(7.11) 
или y = xu, (7.12) 
примет вид: u + xu’ = φ (u), 
, откуда 
.
вместо u. 
или 
.
откуда 
или 
, то есть 
. 
.
, откуда 
(7.17)
. 
или 
. (7.18)
или 
, тогда 
. 
который удовлетворяет начальному условию y (0) = 0.
.
(или 
) 
. 
Тогда 
.
искомую функцию 
и производные искомой функции 
до некоторого порядка включительно.
— известная функция, заданная в некоторой области 
т. е. наивысший из порядков производных, входящих в (1), называется порядком уравнения.
обращается в бесконечность.
и 
входят в это уравнение уже равноправно, и любую из них мы можем принять за независимую переменную.
получаем более симметричное уравнение:
Обратно, всякое уравнение вида (4) можно переписать в виде уравнений (2) или (2′), разрешая его относительно 
или 
так что уравнение (4) равносильно следующим двум уравнениям:
определена на некотором подмножестве 
вещественной плоскости 
Функцию 
определенную в интервале 
мы будем называть решением уравнения (2) в этом интервале*, если:
из интервала 
Это означает, что при любом 
из интервала 
точка 
принадлежит множеству 
и 
этого перевернутого уравнения естественно присоединять к решениям уравнения (2).
ибо она определена и дифференцируема в эгои интервале, и, подставляя се в уравнение (9), получаем тождество:
есть решение равнения 
в интервале 
обращающую уравнение (2) в тождество (7), т. е. решение уравнения (2), называют интегралом этого уравнения. Мы будем употреблять термин интеграл только в смысле п. 16.
.
(7.38)
. Подставляем сюда значение 
и 
из системы, получим 
и подставим в полученное нами уравнение: 
или 
(*) 
(**)
(7.45)
(7.46)
или k 2 – 5k + 4 = 0, корни которого k1 = 1, k2 = 4.
и 
: 
или 
Положив 
получим 
(7.47)
(7.48)
(7.49) 
— действительные числа, которые определяются через 
.
