Что такое порядок числа в алгебре 8 класс
Математика
Числа, подобно единицам, также разделяются на порядки. Так, первые десять чисел называют числами первого порядка. Числа от десяти до ста называют числами второго порядка, от ста до тысячи — числами третьего порядка и т. д.
Названия чисел. При помощи указанных единиц различного порядка мы получаем названия всех остальных чисел. Так, числа, состоящие из одной, двух, трех … единиц второго порядка, или, что то же, одного, двух, трех … десятков, мы называем десять, двадцать (два десять), тридцать, сорок, пятьдесят, шестьдесят, семьдесят, восемьдесят, девяносто. Присоединяя к этим числам девять чисел первого порядка, мы получаем все числа второго порядка. Так, присоединяя к числу десять все числа первого порядка, мы получаем все числа между десятью и двадцатью: одиннадцать, двенадцать (два на десять), тринадцать, четырнадцать, пятнадцать, шестнадцать, семнадцать, восемнадцать, девятнадцать. Присоединяя к двадцати девять чисел первого порядка, получим все числа между двадцатью и тридцатью: двадцать один, двадцать два и т. д. Наибольшее число второго порядка есть девяносто девять.
Десять десятков образуют сотню или сто, единицу третьего порядка. Числа, состоящие из одной или нескольких единиц третьего порядка, мы называем: сто, двести, триста, четыреста, пятьсот, шестьсот, семьсот, восемьсот, девятьсот.
Присоединяя к этим числам все числа первого и второго порядка, мы получаем все числа третьего порядка, например, восемьсот сорок пять, девятьсот четыре. Наибольшее число третьего порядка есть девятьсот девяносто девять.
Десять сот образуют тысячу — единицу четвертого порядка. Повторяя тысячу один, два и т. д. раз, образуем числа: тысяча, две тысячи, три тысячи и т. д. Присоединяя к этим числам все числа первого, второго и третьего порядков, образуем все числа четвертого порядка и т. д.
Десятичная система. Систему счисления, в которой каждые десять единиц низшего образуют единицу следующего высшего порядка, называют десятичною. Она принята в настоящее время всеми образованными народами.
Основание системы. Число десять называется основанием системы. В основе ее лежит число десять.
Полагают, что число десять принято за основание потому, что первоначально люди считают обыкновенно по пальцам.
Пример. Шесть миллионов пятьсот семь тысяч двести семь есть число седьмого порядка. Оно состоит из шести единиц седьмого прядка (шесть миллионов), к которому присоединено число шестого порядка (пятьсот семь тысяч двести семь).
Число шестого порядка состоит из пяти единиц шестого порядка (пятьсот тысяч), к которому присоединено число четвертого порядка (семь тысяч двести семь).
Число четвертого порядка состоит из семи единиц четвертого порядка (семь тысяч), к которому присоединено число третьего порядка (двести семь).
Число третьего порядка состоит из двух единиц третьего порядка (двести), к которому присоединяется число первого порядка (семь).
Число семь состоит из семи простых единиц.
Всякое число содержится между двумя единицами различных порядков. Всякое число более единицы одного порядка и менее единицы следующего высшего порядка. Так, число триста сорок семь более ста и менее тысячи.
Урок алгебры в 8-м классе по теме «Стандартный вид числа» с использованием регионального компонента
Разделы: Математика
Сторона любимая, приметная,
У тебя есть приметы предметные.
Только вот им верить не приходится-
Все они изменчивы, как водится.
Где-то есть такие ж кедры с соснами,
Где-то есть такие ж зимы с вёснами,
Горы есть со снеговыми шапками
И посёлки с трубами и шахтами.
Только нет нигде чего-то главного.
По цене одной лишь жизни равного,
Очень близкого чего-то очень местного,
Сердцу только одному известного.
Стоит лишь откуда-то вернуться,
Как готово сердце захлебнуться,
Весь мой век такое с ним случается.
Пробовал унять – не получается.
Виктор Баянов, известный кузбасский поэт.
ХОД УРОКА
1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.
УЧИТЕЛЬ: Здравствуйте, ребята! Вы, наверное, обратили внимание, что на доске записано стихотворение. Это необычно? Конечно! Но и урок у нас сегодня немного необычный. Мы будем изучать новый материал по алгебре, используя данные о нашем родном крае – Кемеровской области, где мы живём и учимся. (Учитель читает стихотворение кузбасского поэта В. Баянова, являющиеся эпиграфом данного урока.)
Но прежде, чем переходить к новой теме, предлагаю вам провести гимнастику для ума – поработать устно: вспомнить изученные правила, посчитать и подготовиться к знакомству с новой темой.
2. УСТНАЯ РАБОТА.
3). Вычислите: а) 3,2 * 10; б) 0,032 * 100;
в) 0,032*1000; г) 32,3 : 10; д) 32,3 : 100; е) 32,3 : 1000.
3. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.
Рассмотрим некоторые примеры (учитель записывает подробно на доске, объясняет запись, прибегает к помощи обучающихся. Обучающиеся записывают в тетрадях, внимательно слушают, задают вопросы по ходу решения и отвечают на вопросы педагога).
4. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО В ХОДЕ ВЫПОЛНЕНИЯ УПРАЖНЕНИЙ.
(Учитель готовит плакаты формата А4 с записанными на них данными по Кемеровской области. С помощью магнитов плакаты поочередно вывешиваются на доску. После записи очередного числа плакат убирается и заменяется следующим. Картинки с изображением животных и птиц вывешиваются на доску вместе с числом. Учитель комментирует плакаты, появляющиеся на доске. Картинки с изображением птиц и животных можно позаимствовать у учителя биологии или скачать из интернета, привлечь к работе можно учащихся 8 класса по желанию. Из опыта работы хочу сказать, что желающих бывает много, но необходимо помнить и об исполнительской дисциплине каждого ученика. Выполнение задания лучше проверить заранее, чтобы избежать срыва урока).
ПРИМЕР 1. Представьте в стандартном виде следующие величины:
ПРИМЕР 2. Прочтите числа, записанные в стандартном виде:
ЗАДАНИЕ: Представьте указанные данные в стандартном виде. Отметьте в таблице ответы и буквы, им соответствующие. Оставшиеся буквы зачеркните и прочтите название самой крупной из осёдлых птиц Кемеровской области, которая весит до 5 кг.
Стандартный вид числа
Урок 36. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Стандартный вид числа»
Наверняка, в физике, биологии, химии или географии вы сталкивались, как с очень большими, так и очень малыми положительными числами.
Скажите с такими числами удобно выполнять математические расчёты? Конечно же, нет. В обычном десятичном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними какие-либо действия. В таком случае полезным оказывается представление числа в виде
Говорят, что мы записали числа в стандартном виде. В таком виде можно представить любое положительное число.
Стандартным видом числа 
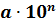
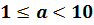

Число 

Если порядок числа 
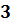
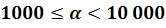
Если порядок числа 
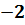
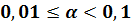
Большой положительный порядок показывает, что число очень велико.
Большой по модулю отрицательный порядок показывает, что число очень мало.
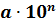
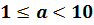

По определению стандартного вида числа следует, что в стандартном виде в целой части числа (до запятой) может содержаться только одна цифра.
Все остальные цифры должны стоять после (справа) от запятой.
Порядок числа даёт представление о том, насколько велико или мало это число.
В стандартном виде можно записать не только большое или малое, но и любое число.
Для того чтобы привести число к стандартному виду, надо:
1. Перенести в нём запятую так, чтобы она была сразу после первой значащей цифры.
2. полученное число умножить на 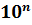

Значащей цифрой числа называют его первую (слева направо) отличную от нуля цифру, а также все последующие за ней цифры.
Пример: представим в стандартном виде число.
Задание: запишите число в стандартном виде.
Задание: запишите в стандартном виде число, равное значению произведения х и у.
Стандартным видом числа 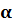
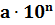
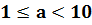
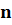
Число 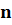
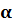
Для того, чтобы привести число к стандартному виду, надо перенести в нём запятую так, чтобы она была сразу после первой значащей цифры, и полученное число умножить на 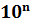
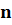
Стандартная форма записи числа, мантисса числа, порядок числа
Положительное число, записанное в стандартной форме, имеет вид
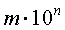
Число m является натуральным числом или десятичной дробью, удовлетворяет неравенству
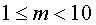
и называется мантиссой числа, записанного в стандартной форме.
Число n является целым числом (положительным, отрицательным или нулем) и называется порядком числа, записанного в стандартной форме.
Например, число 3251 в стандартной форме записывается так:
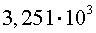
Здесь число 3,251 является мантиссой, а число 3 является порядком.
Стандартная форма записи числа часто используется в научных расчетах и очень удобна для сравнения чисел.
Для того, чтобы сравнить два числа, записанных в стандартной форме, нужно сначала сравнить их порядки. Большим будет то число, порядок которого больше. Если же порядки сравниваемых чисел одинаковы, то нужно сравнить мантиссы чисел. Большим в этом случае будет то число, у которого мантисса больше.
Например, если сравнить между собой записанные в стандартной форме числа
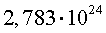
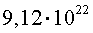
то, очевидно, первое число больше второго, поскольку у него порядок больше.
Если же сравнить между собой числа
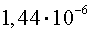
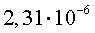
то, очевидно, что второе число больше, чем первое, поскольку порядки у этих чисел совпадают, а мантисса у второго числа больше.
Стандартный вид числа
Представим каждое из чисел 1 083 000 000 000 и 0,0000000003 в виде произведения числа, заключённого между единицей и десятью, и соответствующей степени числа 10:
Говорят, что мы записали числа 1 083 000 000 000 и 0,0000000003 в стандартном виде. В таком виде можно представить любое положительное число.
| Стандартным видом числа а называют его запись в виде а • 10n, где 1 ≤ а Пример 1. Представим в стандартном виде число α = 4 350 000. Пример 2. Представим в стандартном виде число α = 0,000508. Упражнения1013. Назовите порядок числа, представленного в стандартном виде: 1014. Запишите в стандартном виде число: а) 52 000 000; |
1015. Запишите в стандартном виде:
1016. Представьте число в стандартном виде:
а) 1024 000;
б) 6 000 000;
в) 21,56;
г) 0,85;
1017. Масса Земли приближённо равна 6 000 000 000 000 000 000 000 т, а масса атома водорода 0,0000000000000000000017 г. Запишите в стандартном виде массу Земли и массу атома водорода.








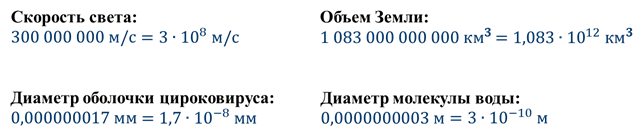

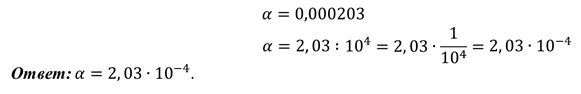


 В числе а поставим запятую так, чтобы в целой части оказалась одна цифра. В результате получим 4,35. Отделив запятой 6 цифр справа, мы уменьшили число α в 10 6 раз. Поэтому а больше числа 4,35 в 10 6 раз. Отсюда
В числе а поставим запятую так, чтобы в целой части оказалась одна цифра. В результате получим 4,35. Отделив запятой 6 цифр справа, мы уменьшили число α в 10 6 раз. Поэтому а больше числа 4,35 в 10 6 раз. Отсюда