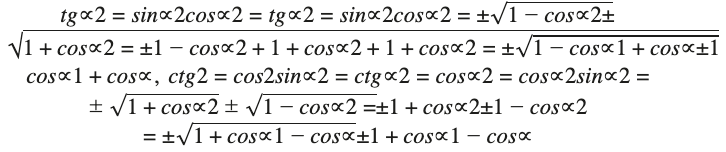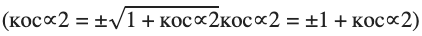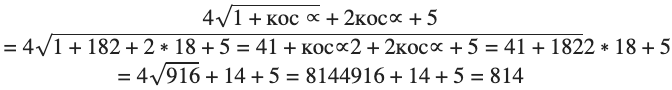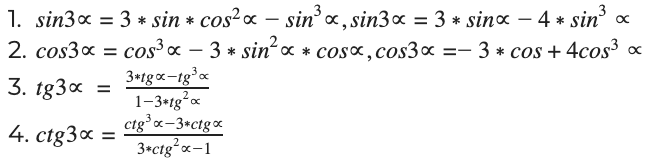Что такое половинный угол

Половинный и тройной аргумент тригонометрической функции: формулы

Содержание:

Синус, косинус, тангенс, котангенс – отношения между выражениями в тригонометрии. Для каждого из них предусмотрена отдельная методика, которая используется при расчете значения. Все функции плотно связаны между собой. Это обуславливает большое количество математических структур. Основные из них обеспечивают:

Формулы половинного аргумента – тригонометрия

Формула половинного аргумента – косинуса или других примеров тригонометрии – это противоположенная конструкциям двойных углов методика. Она основана на использовании угла α для выражения \frac <\alpha> <2>. Все тригонометрические конструкции половинных углов выходят из формул двойного угла.

Выражения для двойных аргументов позволяют выразить значения sinsin2α, coscos2α, tg2α, ctg2α с помощью cossinsinα, tgα, ctgα. В качестве аргумента могут выступать не только углы, но и цельные выражения. Существуют легкий и сложный тип примеров. Общий вид конструкции для расчета половинных аргументов:

Формула половинного аргумента синуса и косинуса

Для выведения уравнения косинусов и синусов половинных углов используется косинус двойных углов:

Для этого необходимо записать их в следующей форме: cos = 1-2 sinα2cosα = 1-2 Sin2α2 cosα=2
Кос2α2-1cosα=2 кос2α2-1

Первое равенство sinα2sinα2 позволяет предположить: \sin \alpha 2 = \pm \sqrt

По аналогии решается второй пример: cosα2cosα2
Косα2 = \pm \sqrt

Формулы половинного аргумента тангенса и котангенса

Для выведения выражений тангенса половинных углов используется стандартная функция: tgα2 = sinα2cosα2tgα2 = sinα2cosα2. Чтобы вывести котангенс, понадобится ctgα2 = cosα2sinα2ctgα2 = cosα2sinα2. Рекомендуется использовать также выражения синуса, косинуса, доказанные ранее.

Формулы половинного аргумента тригонометрических функций: примеры задач

Рассмотрим примеры задач:

1. Необходимо решить пример:

4 кос∝2 + 2 кос∝ + 54 кос∝2 + 5

Для решения задачи используется следующее выражение:

Необходимо упростить пример, для этого действуем:

В итоге получаем: 4 кос∝2 + 2 кос∝ + 5 = 8144 кос∝2 + 2 кос∝ + 5 = 814

2. Необходимо найти решение

кос30°= \sqrt 3 *2кос30°=32

Следует рассчитать половинный угол для тригонометрического функционала косинуса. Для этого:

кос2∝2 = 1 + кос∝2кос2∝2 = 1 + кос∝2

Подставляем существующие данные:

кос2 15°=1 + кос30° 2 = кос 215° = 1 + кос30° 2 = 1+ \sqrt 32 2 = \sqrt 341 + 322 = 2 + 34

В условии заданы параметры кос2 15°кос215°, необходимо вычислить кос15°кос15°.

Место расположения угла в пятнадцать градусов – первая координатная четверть, значение косинуса положительное. Отсюда следует:

кос15°= \sqrt 2 + \sqrt 3 * 4 = кос15°= 2 + 34 = \sqrt 2 + \sqrt 3 * 22 + 32

Решение: кос15°= \sqrt 2 + \sqrt 3 2 кос15° = 2 + 32

Тригонометрические формулы тройного аргумента

Все тригонометрические выражения для двойных, тройных углов называются также формулой для кратных углов. Они используются для выявления тригонометрического функционала углов двойного, тройного типа, через одинарный угол α. В основе операций – сложение. Рассмотрим основные четыре формулы:

Формула синуса тройного аргумента – доказательство

Для доказательства формулы синуса тройных углов применяется сумма и разность между ними. Рекомендуется использование формул для двойных углов. Получаем доказательство:
sin3∝ = sin 2∝ + ∝ = sin3∝ = sin 2∝ + ∝ = sin2∝cos∝ + cos2∝sin∝ = sin2∝ + cos2∝sin∝ = 2sincoscos + cos2∝ — sin2∝*sin∝ = 2sin∝cos∝ + cos2∝ — sin2sin∝ = 3sin∝cos∝ — sin3∝3sin∝cos2∝ — sin3∝

Заменяем на выражение 1-sin2∝1-sin2∝

Косинус тройного аргумента – доказательство

Доказательство формулы косинуса тройных углов выглядит следующим образом:

cos3∝ = cos 2∝ + ∝ = cos 2∝ + ∝ = cos2∝cos∝ — sin2sin∝ = cos2∝cos∝ — sin2∝sin∝ = (cos2∝ — sin2∝) cos∝ — 2sin∝cos∝sin∝ + = (cos2∝ — sin2∝ )*cos∝ — 2sin∝cos∝sin∝ + = cos3∝ — 3sin2∝cos∝cos3∝ — 3sin2∝cos∝.

Проводится замена аргумента. Вместо 3α = cos3α − 3sin2αcosαcos 3α = cos3α — 3sin2αcosα sin2αsin2α вставляем 1 — cos2∝1 — cos2

Итоговое решение: cos3∝ = 4cos3∝ — 3cos∝cos3∝ = 4cos3∝ — 3cos∝

Источник

Формулы половинного угла тригонометрических функций

Формулы половинного угла (половинного аргумента) – это часть от всех основных тригонометрических формул. Они выражают функции синус, косинус, тангенс, котангенс угла `\frac<\alpha>2` через эти ж функции аргумента `\alpha`. Они, можно сказать, противоположны формулам двойного угла. Ниже приведены все формулы половинных углов, их вывод, а также примеры решения задач с их использованием.

Список всех формул половинного угла

Их можно встретить записанными в двух видах. В первом каждая из тригонометрических функций выражается через радикал:

Знак «+» или «-» перед корнями зависит от того, в какую из координатных четвертей попадает угол `\frac<\alpha>2`.

Во втором варианте имеем дело с квадратами тригонометрических функций половинного угла:

Формула синуса и косинуса половинного угла имеет место при любом угле `\alpha`.

Формула тангенса половинного угла справедлива для тех углов `\alpha`, при которых определен `tg \frac \alpha 2`, то есть при ` \alpha\ne\pi+2\pi n, \ n \in Z`.

Формула котангенса выполняется для тех `\alpha`, при которых определен `ctg \frac \alpha 2`, то есть при ` \alpha\ne 2\pi n, \ n \in Z`.

С помощью следующего набора формул можно выразить каждую из тригонометрических функций угла `\alpha` через тангенс половинного угла.

`sin \ \alpha= \frac<2tg\frac<\alpha><2>><1 + tg^<2>\frac<\alpha><2>>,` ` \alpha\ne \pi +2\pi n, n \in Z`
`cos \ \alpha= \frac<1 — tg^<2>\frac<\alpha><2>><1 + tg^<2>\frac<\alpha><2>>,` ` \alpha \ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac<2tg\frac<\alpha><2>><1 — tg^<2>\frac<\alpha><2>>,` ` \alpha \ne \pi +2\pi n, n \in Z,` ` \alpha \ne \frac<\pi><2>+ \pi n, n \in Z`
`ctg \ \alpha = \frac<1 — tg^<2>\frac<\alpha><2>><2tg\frac<\alpha><2>>,` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`

Вывод формул половинного угла

Формула косинуса и синуса половинного угла выводится из формул косинуса двойного угла `cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1`. Запишем их в следующем виде: `cos \alpha=1-2 \ sin^2 \frac \alpha 2` и `cos \alpha=2 \ cos^2 \frac \alpha 2-1`. Выразив из первого равенства ` sin \frac \alpha 2` получим `sin \ \frac \alpha 2=\pm \sqrt<\frac <1-cos \ \alpha>2>`. Аналогично разрешив второе равенство относительно ` cos \frac \alpha 2` в результате будем иметь `cos \ \frac \alpha 2=\pm \sqrt<\frac <1+cos \ \alpha>2>`.

Формулы тангенса и котангенса половинного угла можно вывести, используя определения этих функций в виде `tg \frac \alpha 2=\frac` и `ctg \frac \alpha 2=\frac`, а также две уже доказанные выше формулы для синуса и косинуса.

Примеры использования при решении задач

Пример 1. Найти `cos 15^\circ`, если известно, что `cos 30^\circ=\frac<\sqrt3>2`.

Решение. Формула половинного угла для тригонометрической функции косинус имеет вид `cos^2 \ \frac \alpha 2=\frac <1+cos \ \alpha>2`. Подставив известные значения, имеем `cos^2 15^\circ=\frac <1+cos 30^\circ>2=` `\frac<1+\frac<\sqrt3>2>2=\frac<2+\sqrt3>4`. Имея значение `cos^2 15^\circ`, найдем `cos 15^\circ`. Поскольку угол 15 градусов лежит в первой координатной четверти, а косинус в этой четверти имеет знак «+», то `cos 15^\circ=\sqrt<\frac<2+\sqrt3>4>=` `\frac<\sqrt<2+\sqrt3>>2`.

Пример 2. Вычислить значение выражения `4cos \frac <\alpha>2+2cos \alpha+5`, если `cos \alpha=\frac <1>8`.

Решение. Используя ту же формулу, что и в первом примере (`cos \ \frac \alpha 2=\pm \sqrt<\frac <1+cos \ \alpha>2>`) и известное значение косинуса, упростим выражение: `4\sqrt<\frac <1+cos \ \alpha>2>+2cos \alpha+5=4\sqrt<\frac <1+\frac <1>8>2>+2 \cdot \frac <1>8+5=` `4\sqrt<\frac <9>16>+\frac<1>4+5=8\frac<1>4`.

Ответ. `4cos \frac <\alpha>2+2cos \alpha+5=8\frac<1>4`.

Еще несколько примеров с подробным объяснением посмотрите на видео:

В большинстве случаев формулы половинного угла используются при преобразовании тригонометрических выражений.

Источник

Формулы половинного угла

Что такое формулы половинного угла в тригонометрии

Формулами половинного угла называют выражение синуса, косинуса, тангенса и котангенса угла α /₂ через тригонометрическую функцию данного угла α.

Все формулы половинного угла даны для вычисления квадрата функции. Выражение решается до конца с помощью нахождения арифметического квадратного корня, т.е.:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Знак, стоящий перед ответом, обозначает координатную четверть, в которой находится угол \(\frac\alpha2. \)

Доказательство формул половинного угла

Данное доказательно основано на формулах косинуса двойного угла:

И основных тригонометрических тождествах:

Вывод с доказательством через синус, косинус, тангенс и котангенс

Для доказательства формул синуса и косинуса половинного угла используем формулы косинуса двойного угла.

Решим первое равенство относительно \(\sin^2\left(\frac\alpha2\right)\) для выведения синуса

Решим второе уравнение относительно \(\sin^2\left(\frac\alpha2\right)\) для выведения косинуса.

Перейдем к приведению тангенса и котангенса половинного угла через тригонометрические тождества.

Пример задачи с решением

Задача 1

Косинус угла в 30 градусов равен \(\frac<\sqrt3>2.\)

Найдите косинус угла в 15 градусов.

Решение

Воспользуемся формулой половинного угла для косинуса. Получим:

Угол в 15 градусов находится в первой координатной четверти. Следовательно, его косинус будет являться положительным.

Источник

Формулы двойного и половинного аргумента. Универсальная подстановка

п.1. Формулы двойного аргумента

Выведем формулы двойного аргумента, исходя из формул суммы (см. §13 и §14 данного справочника)

\begin sin2\alpha=sin(\alpha+\alpha)=sin\alpha cos\alpha+cos\alpha sin\alpha=2sin\alpha cos\alpha\\ cos2\alpha=cos(\alpha+\alpha)=cos\alpha cos\alpha-sin\alpha sin\alpha=cos^2\alpha-sin^2\alpha\\ tg2\alpha=tg(\alpha+\alpha)=\frac<1-tg\alpha\cdot tg\alpha>=\frac<2tg\alpha> <1-tg^2\alpha>\end

Умножим полученное выражение на котангенс вверху и внизу дроби, и получим еще одно полезное выражение:

Например:
Найдем \(sin2\alpha\) и \(tg2\alpha\), если \(sin\alpha=0,8,\ \frac\pi2\lt\alpha\lt\pi\)
Угол \(\alpha\) во 2-й четверти, косинус отрицательный:
\(cos\alpha=-\sqrt<1-sin^2\alpha>=-\sqrt<1-0,8^2>=-0,6\)
\(tg\alpha=\frac=\frac<0,8><-0,6>=-\frac43\)
Синус двойного угла: \(sin2\alpha=2sin\alpha cos\alpha=2\cdot 0,8\cdot(-0,6)=-0,96\)
Тангенс двойного угла: \(tg2\alpha=\frac<2tg\alpha><1-tg^2\alpha>=\frac<2\cdot \left(-\frac43\right)><1-\left(-\frac43\right)^2>=\frac<-\frac83><1-\frac<16><9>>=\frac83 : \frac79=\frac83\cdot\frac97=\frac<24><7>=3\frac37\)

п.2. Формулы половинного аргумента

По формуле двойного аргумента для косинуса: \(cos2\alpha=2cos^2\alpha-1\)
Заменим слева угол \(2\alpha\rightarrow \alpha\), а справа угол \(\alpha\rightarrow\frac<\alpha><2>\).
Получаем: \begin cos\alpha=2cos^2\frac<\alpha><2>-1\Rightarrow 2cos^2\frac<\alpha><2>=1+cos\alpha\Rightarrow cos^2\frac<\alpha><2>=\frac<1+cos\alpha> <2>\end Из другой формулы двойного аргумента для косинуса: \(cos2\alpha=1-2sin^2\alpha\), получаем: \begin cos\alpha=1-2sin^2\frac<\alpha><2>\Rightarrow 2sin^2\frac<\alpha><2>=1-cos\alpha\Rightarrow sin^2\frac<\alpha><2>=\frac<1-cos\alpha> <2>\end Для квадрата тангенса и котангенса половинного угла: \begin tg^2\frac<\alpha><2>=\frac<2>><2>>=\frac<1-cos\alpha><1+cos\alpha>,\ \ \ ctg^2\frac<\alpha><2>=\frac<1><2>>=\frac<1+cos\alpha> <1-cos\alpha>\end

п.3. Формулы универсальной подстановки

Универсальная подстановка эффективна при решении тригонометрических уравнений, а также интегрировании.

п.4. Примеры

в) \( \sqrt<2+\sqrt<2+2cos4\alpha>> \), где \(0\le \alpha\le\frac\pi2\) \begin \sqrt<2+\sqrt<2+2cos4\alpha>>=\sqrt<2+\sqrt<2(1+cos4\alpha)>>=\sqrt<2+\sqrt<2\cdot 2cos^2 2\alpha>>=\\ =\sqrt<2+2\cdot |cos2\alpha|>=\sqrt<2(1+|cos2\alpha|)>= \left[ \begin \sqrt<2(1+cos2\alpha)>,\ \ cos2\alpha\geq 0\\ \sqrt<2(1-cos2\alpha)>,\ \ cos2\alpha\lt 0 \end \right. =\\ = \left[ \begin \sqrt<2\cdot 2cos^2\alpha>,\ \ 0\leq 2\alpha\leq\frac\pi2\\ \sqrt<2\cdot 2sin^2\alpha>,\ \ \frac\pi2\lt 2\alpha\leq \pi \end \right. = \left[ \begin 2cos\alpha,\ \ 0\leq \alpha\leq\frac\pi4\\ 2sin\alpha,\ \ \frac\pi4\lt \alpha\leq \frac\pi2 \end \right. \end Ответ: \(2cos\alpha\) при \(0\leq \alpha\leq\frac\pi4;\ \ 2sin\alpha\) при \(\frac\pi4\lt \alpha\leq \frac\pi2\)
г) \( 4(sin^4x+cos^4x)-4(sin^6x+cos^6x)-1 \)
Основное тригонометрическое тождество: \(sin^2x+cos^2x=1\)
Возведём в квадрат: \begin (sin^2x+cos^2x)^2=sin^4x+cos^4x+2sin^2x cos^2x=1\\ sin^4x+cos^4x=1-\frac<(2sinx cosx)^2><2>=1-\frac <2>\end Возведём в куб: \begin (sin^2x+cos^2x)^3=sin^6x+cos^6x+3sin2x cos^4x+3sin^4x cos^2x=1\\ sin^6x+cos^6x = 1-3sin^2x cos^2x\underbrace<(cos^2x+sin^2x)>_<=1>=\\ =1-\frac34(2sinx cosx)^2=1-\frac<3sin^2 2x> <4>\end

Подставляем: \begin 4\left(1-\frac<2>\right)-4\left(1-\frac<3sin^2 2x><4>\right)=1=4-2sin^2 2x-4+3sin^2 2x-1=\\ =sin^2 2x-1=-cos^2 2x \end Ответ: \(-cos^2 2x\)

Источник

Основные тригонометрические формулы и тождества sin, cos, tg, ctg

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

На основе формул сложения выводятся тригонометрические формулы кратного угла.

Формулы кратного угла: двойного, тройного и т.д.

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

Формулы понижения степени

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

Произведение тригонометрических функций

Формулы произведения тригонометрических функций

Универсальная тригонометрическая подстановка

Универсальная тригонометрическая подстановка

Источник