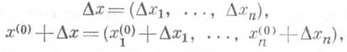Что такое полное приращение

ПОЛНОЕ ПРИРАЩЕНИЕ

Смотреть что такое «ПОЛНОЕ ПРИРАЩЕНИЕ» в других словарях:

Полное приращение — приращение, приобретаемое функцией нескольких переменных, когда все аргументы получают (вообще говоря, не нулевые) приращения Δx1, Δx2. Δxn. При некоторых условиях (например, если все частные производные непрерывны) П. п. можно… … Большая советская энциклопедия

приращение — [сокращение] ширины штриха : Степень увеличения [уменьшения] ширины штриха символа штрихового кода, обусловленная процессами воспроизведения и способами печати Источник: ГОСТ 30721 2000: Автоматическая идентификация. Кодирование штриховое.… … Словарь-справочник терминов нормативно-технической документации

приращение абсолютной продольной (поперечной) деформации образца — приращение абсолютной продольной (поперечной) деформации образца … Справочник технического переводчика

Приращение абсолютной продольной (поперечной) деформации образца — Dl1,Dl2 Полное укорочение (удлинение) линейных абсолютных размеров образца в пределах базы измерения деформации вдоль (поперек) образующей, вызванное осевой сжимающей силой Источник: ГО … Словарь-справочник терминов нормативно-технической документации

Приращение абсолютной продольной (поперечной) деформации образца — – бет. полное укорочение (удлинение) линейных абсолютных размеров образца в пределах базы измерения деформации вдоль (поперек) образующей, вызванное осевой сжимающей силой. [ГОСТ 24452 80] Рубрика термина: Испытания бетона Рубрики… … Энциклопедия терминов, определений и пояснений строительных материалов

ПЛЯЦЕНТА — ПЛЯЦЕНТА. Содержание: I. Сравнительная анатомил. 55. 1 II. Развитие П. у человека. 556 III. Плацента доношенного плодного яйца. 5Е8 IV. Физиология и биология 11. 55а V. Патология П. Пат. формы II. j … Большая медицинская энциклопедия

Термодинамика — наука о наиболее общих свойствах макроскопических систем, находящихся в состоянии термодинамического равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундаментальных принципов (начал), которые являются… … Большая советская энциклопедия

ТЕРМОДИНАМИКА — наука о наиб. общих св вах макроскопич. физ. систем, находящихся в состоянии термодинамич. равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундам. принципов (начал), к рые явл. обобщением многочисл. наблюдений и… … Физическая энциклопедия

Теплота — 1) Т. мы называем причину, вызывающую в нас специфические, всем известные тепловые ощущения. Источником этих ощущений являются всегда какие либо тела внешнего мира, и, объективируя наши впечатления, мы приписываем этим телам содержание некоторого … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

Источник

Частное и полное приращение функции

Вы будете перенаправлены на Автор24

Таким образом, имеем:

Записать частные и полное приращение функции

Решение:

По определению частного приращения найдем:

По определению полного приращения найдем:

Готовые работы на аналогичную тему

Решение:

По определению частного приращения найдем:

По определению полного приращения найдем:

\[\Delta _ z=(1+0,1)\cdot 2=2,2\] \[\Delta _ z=1\cdot (2+0,1)=2,1\] \[\Delta z=(1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]

Проверить утверждение замечания для функции

Решение:

\[\Delta _ z+\Delta _ z=x+\Delta x+y+(x+y+\Delta y)=2\cdot (x+y)+\Delta x+\Delta y.\]

\[2\cdot (x+y)+\Delta x+\Delta y\ne x+\Delta x+y+\Delta y,\]

\[\Delta _ z+\Delta _ z\ne \Delta z.\]

Для функции от трех и более переменных, аналогично как для функции двух переменных определяются частные приращения по каждой из переменных:

Записать частные и полное приращение функции

Решение:

По определению частного приращения найдем:

По определению полного приращения найдем:

Решение:

По определению частного приращения найдем:

По определению полного приращения найдем:

\[\Delta _ w=(1+0,1)\cdot 2\cdot 1=2,2\] \[\Delta _ w=1\cdot (2+0,1)\cdot 1=2,1\] \[\Delta _ w=1\cdot 2\cdot (1+0,1)=2,2\] \[\Delta z=(1+0,1)\cdot (2+0,1)\cdot (1+0,1)=1,1\cdot 2,1\cdot 1,1=2,541.\]

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 03 2021

Источник

Полное приращение и полный дифференциал

Вы будете перенаправлены на Автор24

Записать полное приращение заданной функции

Решение:

По определению полного приращения некоторой функции найдем:

Решение:

По определению полного приращения некоторой функции найдем:

\[\Delta z=(1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]

Готовые работы на аналогичную тему

Для функции трех и более переменных, аналогично как для функции двух переменных определяются полное приращение:

Записать полное приращение заданной функции

Решение:

По определению полного приращения некоторой функции найдем:

Решение:

По определению полного приращения некоторой функции найдем:

\[\Delta z=(1+0,1)\cdot (2+0,1)\cdot (1+0,1)=1,1\cdot 2,1\cdot 1,1=2,541.\]

\[dz=f’_ (x,y)\cdot \Delta x+f’_ (x,y)\cdot \Delta y.\]

Записать полный дифференциал заданной функции

Решение:

Определим частные производные заданной функции:

По определению полного дифференциала некоторой функции найдем:

\[dz=1\cdot \Delta x+2\cdot \Delta y=\Delta x+2\cdot \Delta y.\]

Решение:

Определим частные производные заданной функции:

По определению полного дифференциала некоторой функции найдем:

\[dz=y\cdot \Delta x+x\cdot \Delta y.\]

Для функции трех и более переменных, аналогично как для функции двух переменных определяются полный дифференциал:

\[dw=f’_ (x,y,z)\cdot \Delta x+f’_ (x,y,z)\cdot \Delta y+f’_ (x,y,z)\cdot \Delta z,\] \[dw=f’_ (x,y,z. t)\cdot \Delta x+f’_ (x,y,z. t)\cdot \Delta y+. +f’_(x,y,z. t)\cdot \Delta t.\]

Записать полный дифференциал заданной функции

Решение:

Определим частные производные заданной функции:

По определению полного дифференциала некоторой функции найдем:

\[dz=z\cdot \Delta x+z\cdot \Delta y+(x+y)\cdot \Delta z.\]

В новых обозначениях выражения для полного дифференциала принимает следующий вид:

Функция, имеющая непрерывные частные производные в заданной точке, является дифференцируемой в данной точке, при этом полный дифференциал функции в данной точке равен сумме произведений частных производных на дифференциалы независимых переменных соответственно.

Записать полный дифференциал заданной функции

Решение:

Определим частные производные заданной функции:

По определению полного дифференциала некоторой функции найдем:

\[dz=z\cdot dx+0\cdot dy+x\cdot dz=z\cdot dx+x\cdot dz.\]

Решение:

Определим частные производные заданной функции:

По определению полного дифференциала некоторой функции найдем:

\[dz=y\cdot dx+x\cdot dy.\]

Запишем полный дифференциал в заданной точке:

\[dz|_ <(1,2)>=2\cdot dx+1\cdot dy=2dx+dy.\]

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 08 04 2021

Источник

Полное приращение

Смотреть что такое «Полное приращение» в других словарях:

приращение — [сокращение] ширины штриха : Степень увеличения [уменьшения] ширины штриха символа штрихового кода, обусловленная процессами воспроизведения и способами печати Источник: ГОСТ 30721 2000: Автоматическая идентификация. Кодирование штриховое.… … Словарь-справочник терминов нормативно-технической документации

приращение абсолютной продольной (поперечной) деформации образца — приращение абсолютной продольной (поперечной) деформации образца … Справочник технического переводчика

Приращение абсолютной продольной (поперечной) деформации образца — Dl1,Dl2 Полное укорочение (удлинение) линейных абсолютных размеров образца в пределах базы измерения деформации вдоль (поперек) образующей, вызванное осевой сжимающей силой Источник: ГО … Словарь-справочник терминов нормативно-технической документации

Приращение абсолютной продольной (поперечной) деформации образца — – бет. полное укорочение (удлинение) линейных абсолютных размеров образца в пределах базы измерения деформации вдоль (поперек) образующей, вызванное осевой сжимающей силой. [ГОСТ 24452 80] Рубрика термина: Испытания бетона Рубрики… … Энциклопедия терминов, определений и пояснений строительных материалов

ПЛЯЦЕНТА — ПЛЯЦЕНТА. Содержание: I. Сравнительная анатомил. 55. 1 II. Развитие П. у человека. 556 III. Плацента доношенного плодного яйца. 5Е8 IV. Физиология и биология 11. 55а V. Патология П. Пат. формы II. j … Большая медицинская энциклопедия

Термодинамика — наука о наиболее общих свойствах макроскопических систем, находящихся в состоянии термодинамического равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундаментальных принципов (начал), которые являются… … Большая советская энциклопедия

ТЕРМОДИНАМИКА — наука о наиб. общих св вах макроскопич. физ. систем, находящихся в состоянии термодинамич. равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундам. принципов (начал), к рые явл. обобщением многочисл. наблюдений и… … Физическая энциклопедия

Теплота — 1) Т. мы называем причину, вызывающую в нас специфические, всем известные тепловые ощущения. Источником этих ощущений являются всегда какие либо тела внешнего мира, и, объективируя наши впечатления, мы приписываем этим телам содержание некоторого … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

Источник

Полное приращение и полный дифференциал функции многих переменных

Полное приращение и полный дифференциал функции многих переменных

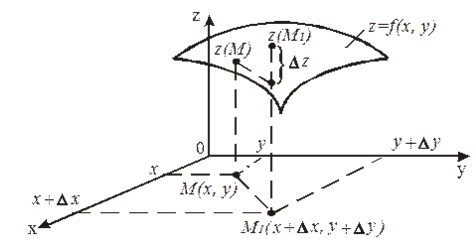
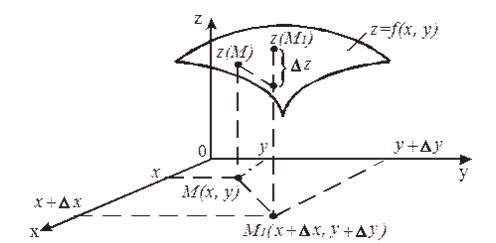
Пусть z = f (x, y) — функция двух переменных. Дадим обоим переменным приращения соответственно Δx и Δy, тогда функция z получит приращение Δz = f (x + Δx; y + Δy) – f (x, y), которое называется полным приращением функции.

Известно, что для функции y = φ (x), которая имеет производную y’= φ’ (x), приращение функции можно представить в виде
Δy = φ ‘(x) ⋅ Δx + εΔx, (5.8)
где ε → 0, если Δx → 0.

Тогда главная линейная часть приращения функции называется дифференциалом функции dy = φ’ (x) Δx = φ’ (x) dx.

В случае функции двух или более переменных наличие частных производных еще не гарантирует того, что полное приращение функции можно представить в виде, аналогичном (5.8).

Определение 6. Функция z = f (x, y) называется дифференцируемой в данной точке M (x; y), если ее полное приращение в этой точке можно представить в виде:
(5.9)
где при Δx → 0, Δy → 0, а A и B — не зависят от приращений Δx, Δy.

Слагаемые и являются, очевидно, бесконечно малыми величинами высшего порядка малости, чем Δx и Δy.

Определение 7. Полным дифференциалом функции z = f (x; y) называется главная линейная часть приращения функции относительно Δx и Δy, то есть: dz = A⋅ Δx + B⋅ Δy или dz = Adx + Bdy.

ТЕОРЕМА 1. Если функция z = f (x; y) дифференцируема в данной точке M (x; y), то существуют частные производные этой функции и имеет место равенство то есть
(5.10)

Поскольку A — постоянная величина (x и y фиксированные), то

Аналогично доказывается, что Таким образом, формула (5.10) доказана.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник