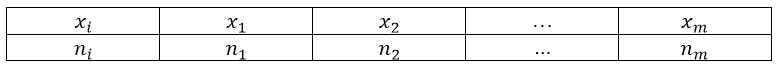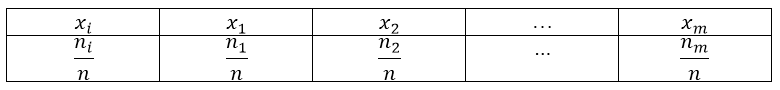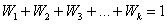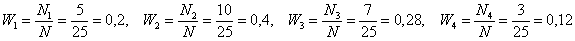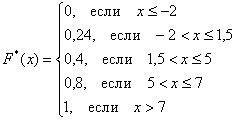Что такое полигон в математике
Полигон частот
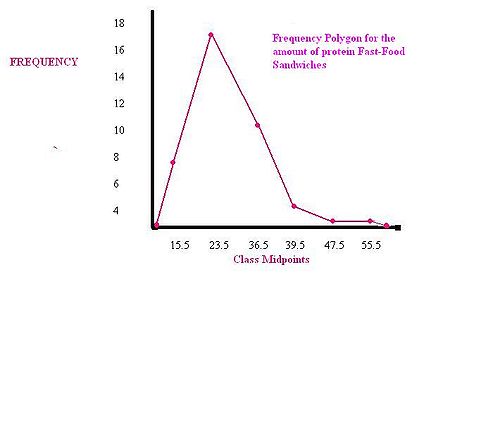
Полиго́н часто́т (в математической статистике) — один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.
Ссылки
См. также
Полезное
Смотреть что такое «Полигон частот» в других словарях:
Полигон (значения) — Полигон: Полигон участок суши или моря, который предназначен для испытаний различных видов техники. Военный полигон объект для проведения войсковых учений или испытаний вооружений и военной техники. Полигон оборудованная территория,… … Википедия
полигон — 3.30 полигон: Испытательное средство и средство обучения персонала заказчика. Обеспечивает создание готовой к внедрению и предварительно проверенной (в условиях полигона) АСУТП или ее компонентов. Полигон АСУТП, оснащенный специальными средствами … Словарь-справочник терминов нормативно-технической документации
полигон кумулятивных частот — 2.19. полигон кумулятивных частот Ломаная линия, получаемая при соединении точек, абсциссы которых равны верхним границам классов, а ординаты либо кумулятивным абсолютным частотам, либо кумулятивным относительным частотам Источник: ГОСТ Р… … Словарь-справочник терминов нормативно-технической документации
ПОЛИГОН — – ломаная линия, соединяющая точки, соответствующие величинам частот, откладываемых по осям ординат [2, c. 67; 16, c.46; 89, c. 175] … Современный образовательный процесс: основные понятия и термины
ЧАСТОТ ПОЛИГОН — Способ рисуночного представления плотности распределения. Частота каждого интервала класса (см. групповая плотность распределения) откладывается на графике, и проводится линия, соединяющая эти точки. Эта линия называется гистограммой … Толковый словарь по психологии
РАСПРЕДЕЛЕНИЯ ПОЛИГОН — график распределения частот для порядковых и количественных переменных ( также Шкала измерительная). Представляет собой ломаную линию, наглядно демонстрирующую распределение частот. Линия Р.П. соединяет точки, координаты которых для дискретных и… … Социология: Энциклопедия
РАСПРЕДЕЛЕНИЕ ЧАСТОТЫ — Любое распределение, основанное на перечислении частоты встречаемости значений, согласно классам или категориям. Таким образом, каждому набору классов присваивается номер, который представляет наблюдаемую частоту. Независимо от метода… … Толковый словарь по психологии
НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ СТАТИСТИКИ — методы математич. статистики, не предполагающие знания функционального вида генеральных распределений. Название непараметрические методы подчеркивает их отличие от классических параметрических методов, в к рых предполагается, что генеральное… … Математическая энциклопедия
Гистограмма — Пример гистограммы У этого термина существуют и другие значения, см. Гистограмма (значения). Гистограмма (от др. греч … Википедия
КРИВАЯ РАСПРЕДЕЛЕНИЯ — – это предел, к которому стремится полигон частот при неограниченном увеличении объема статистической совокупности и уменьшения интервалов (увеличение точности измерения, переход от дискретной величины к непрерывной) [73, c. 16; 89, c. 178] … Современный образовательный процесс: основные понятия и термины
Постройка полигона и гистограммы частот
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
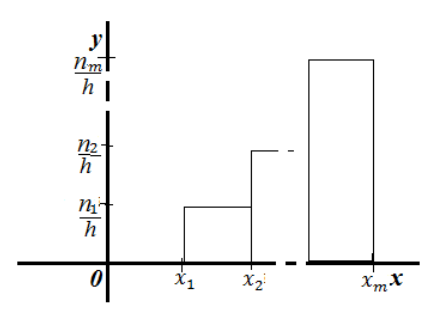
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2). (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
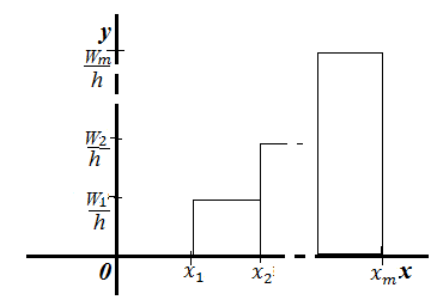
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2). (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
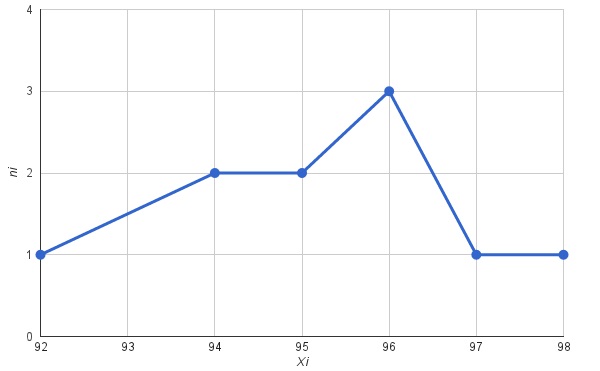
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
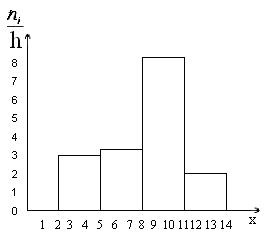
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
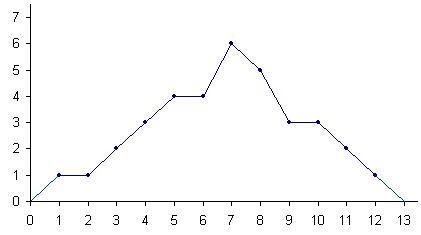
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Полигон частот и гистограмма частот
Вы будете перенаправлены на Автор24
Полигон частот
Пусть нам дан ряд распределения, записанный с помощью таблицы:
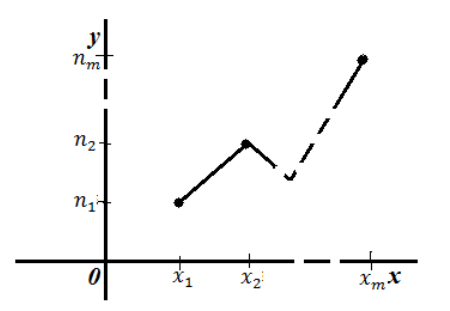
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие частоты. Полученные точки соединяют ломанной:
Рисунок 2. Полигон частот.
Помимо обычной частоты существует еще понятие относительной частоты.
Получаем следующую таблицу распределения относительных частот:
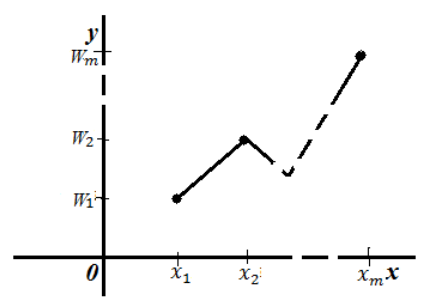
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие относительные частоты. Полученные точки соединяют ломанной:
Рисунок 4. Полигон относительных частот.
Гистограмма частот
Помимо понятия полинома для непрерывных значений существует понятие гистограммы.
Рисунок 5. Гистограмма частот.
Готовые работы на аналогичную тему
Рисунок 6. Гистограмма относительных частот.
Примеры задачи на построение полигона и гистограммы
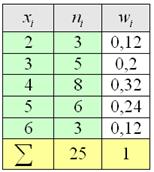
Пусть распределение частот имеет вид:
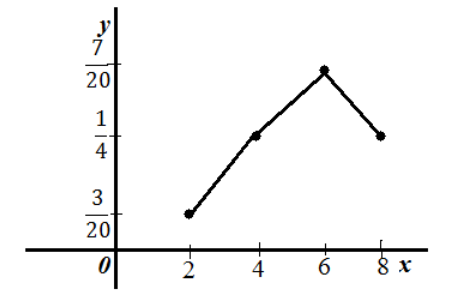
Построить полигон относительных частот.
Получим следующий полигон относительных частот.
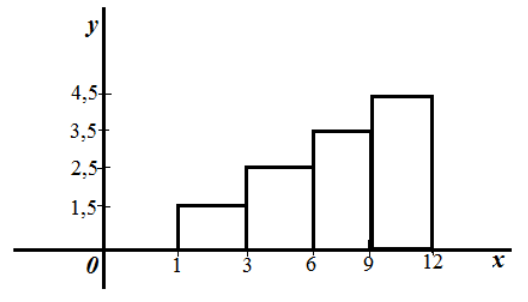
Дан ряд непрерывного распределения частот:
Получаем следующую гистограмму частот:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 25 02 2021
2. Дискретный вариационный ряд.
Полигон частот и эмпирическая функция распределения
На вводном уроке по математической статистике мы узнали, что такое математическая статистика, и теперь обо всём подробнее. Далее для удобства я буду нумеровать статьи и постараюсь делать их не слишком длинными. Потому что всё действительно просто, и главное, здесь научиться рациональной технике вычислений, на которую и будет сделан особый упор.
Интервальные и дискретные вариационные ряды почти сразу же встретились в предыдущей статье, и мы начинаем с дискретного случая, когда количественная эмпирическая величина 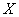
…что-то не понятно по терминам? Срочно изучать первый урок! (ссылка выше)
Дискретный вариационный ряд – это упорядоченное по возрастанию (как правило) множество вариант 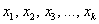
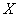
Частоты выборочной совокупности обозначают через 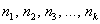
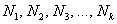
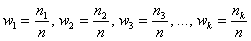
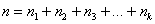
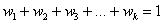
Аналогично для совокупности генеральной: 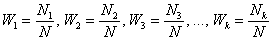
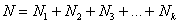
И тут вспоминается Пример 2 об оценках по матанализу в группе из 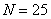
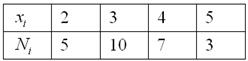
– пожалуйста, пример дискретного вариационного ряда, где варианты 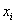
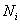
Для разминки найдём относительные частоты:
и непременно проконтролируем, что: 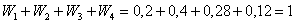
Все вычисления обычно проводят на калькуляторе либо в Экселе, а результаты заносят в таблицу, при этом, в статистике данные чаще располагают не в строках, а в столбцах: 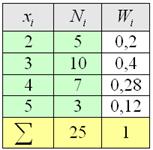
Такое расположение обусловлено тем, что количество вариант может быть достаточно велико, и они просто не вместятся в строчку. Не редкость, когда их 10-20, а бывает, и 100-200, что тоже и неоднократно встречалось в моей практике. И это не какие-то супер-пупер расчёты, а учебные задачи!
После сей позитивной новости продолжаем 🙂
Откуда берутся дискретные вариационные ряды? Такие ряды появляются в результате учёта дискретной характеристики статистической совокупности, причём, варианты ряда не отличаются большим разнообразием. Например, оценки (коих не так много) в примере выше.
И сейчас мы примем непосредственное участие в этом процессе:
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3. Требуется:
– составить вариационный ряд и построить полигон частот;
– найти относительные частоты и построить эмпирическую функцию распределения.
Чего томиться? – вся тема урока в одной задаче!
Решение: в условии прямо сказано о том, что перед нами выборка из генеральной совокупности (всех рабочих цеха), и первое, что логично сделать – подсчитать её объем, т.е. количество рабочих. В данном случае это легко сделать устно: 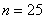
Квалификационные разряды – есть величина дискретная, и поэтому нам предстоит составить дискретный вариационный ряд (обратите внимание, что в условии ничего не сказано о характере ряда).
Если у вас под рукой нет вычислительных программ, то вручную (Эксель разберём ниже). При этом оптимальным может быть следующий алгоритм: сначала окидываем взглядом все числа и определяем среди них минимальное (примерно) и максимальное (примерно). В данном случае ориентировочный диапазон – от 1 до 7. Записываем их в столбец на черновике и обводим в кружочки. Далее начинаем вычёркивать карандашом числа из исходного списка: 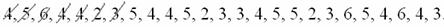
и делать около соответствующих кружков засечки:
После того, как все числа будут вычеркнуты, подсчитываем количество засечек в каждой строке: 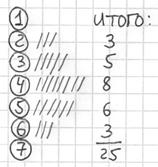
И обязательно проверяем, получается ли у нас в сумме объём выборки 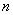
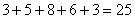

…ну что же, вполне и вполне логично – рабочих средней квалификации много, а учеников и мастеров – мало. Полученные результаты позволяют достаточно точно судить об уровне квалификации всего цеха (если, конечно, выборка представительна)
Построенный вариационный ряд также называют статистическим распределением выборки, причём, этот термин применИм не только для дискретного, но и для интервального ряда, который мы рассмотрим на следующем уроке.
Построим полигон частот. Это статистический аналог многоугольника распределения дискретной случайной величины (кто изучал). Полигон частот – это ломаная, соединяющая соседние точки 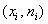
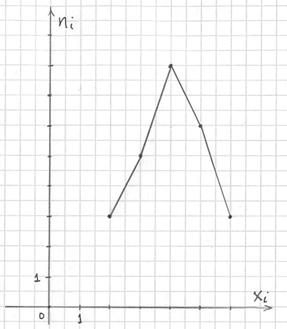
…эх, ностальгия. Но, пятилетку-другую, думается, так решать ещё будут.
Теперь современный способ:
Решаем! – исходные данные с пошаговой инструкцией прилагаются.
Вторая часть задачи. Найдём относительные частоты 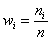
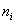

– обязательно проверяем, что сумма относительных частот равна единице!
Иногда требуется построить полигон относительных частот. Как вы правильно догадываетесь – это ломаная, соединяющая соседние точки 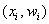
А теперь посмотрим на относительные частоты и задумаемся, на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что 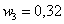
А вот если учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты 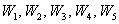
Построим эмпирическую функцию распределения 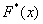
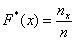
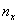
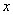
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
Очевидно, что на интервале 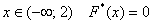
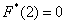
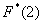
На промежутке 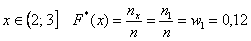
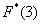
На промежутке 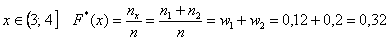
– если 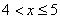

– если 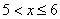
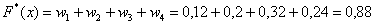
– и, наконец, если 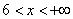
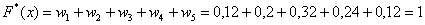
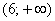
Накопленные относительные частоты удобно записывать в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева 1-е значение (красная стрелка), а каждое следующее получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения): 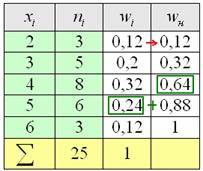
Вот, кстати, ещё один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
Саму функцию принято записывать в кусочном виде:
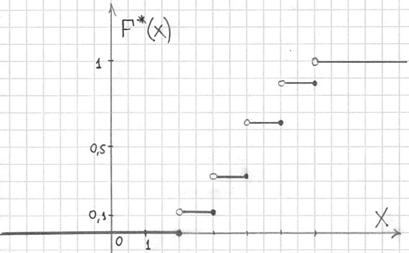
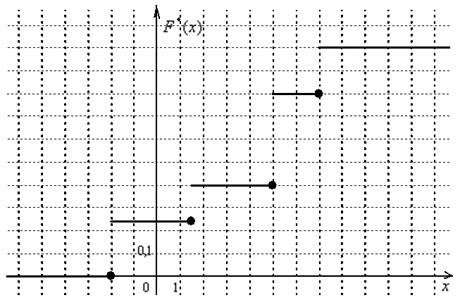
а её график представляет собой ступенчатую фигуру:
Эмпирическая функция распределения не убывает и принимает значения из промежутка 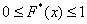
И сейчас мы автоматизируем процесс; видео, к сожалению, не вписалось по ширине, посему смотрим его на Ютубе:

Эмпирическая функция распределения 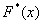
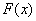
Миниатюрная задача для закрепления материала:
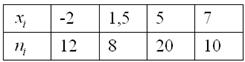
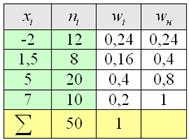
Дано статистическое распределение выборки
Составить эмпирическую функцию распределения, выполнить чертёж
Самостоятельно решить Пример 5 в Экселе, все числа и обозначения уже там.
Свериться с образцом можно ниже. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.
И я жду вас на третьем уроке, где речь пойдёт об интервальном вариационном ряде.
Пример 5. Решение: заполним расчётную таблицу:
Составим эмпирическую функцию распределения:
Выполним чертёж:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5