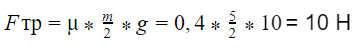Что такое покоится в физике
Отношение движения тела и покоя
Физическое тело, существующее в собственном времени и собственном пространстве, находится либо в состоянии движения, либо в состоянии покоя. Темой данной работы является отношение друг к другу неразличимых состояний движения тела и покоя и различимых состояний движения и покоя тела.
Великий итальянский физик и астроном, создатель основ механики Г. Галилей (1564-1642) установил закон инерции:
| если на тело не действуют никакие другие тела, то оно сохраняет состояние покоя или равномерного прямолинейного движения относительно Земли. |
В нём Земля принималась за инерциальное тело, на которое не действуют другие тела и которое сохраняет состояние покоя или равномерного прямолинейного движения. Признаком инерциальных тел и систем было принято такое их отношение к Земле, при котором они сохраняют состояние покоя или равномерного прямолинейного движения.
Позже, когда было доказано, что Земля вращается вокруг своей оси и совершает годовое обращение вокруг Солнца, она уже не могла считаться инерциальной системой отсчёта для всех остальных инерциальных тел и систем. Формулировка закона инерции Галилея не должна была содержать понятия Земли.
Великий английский физик, астроном и математик, основоположник классической механики И. Ньютон (1642-1727) обновил формулировку закона инерции Галилея:
| всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействия со стороны других тел не заставят его изменить это состояние. |
Признаком инерциальных систем было принято их соответствие второму закону Ньютона.
Закон инерции Галилея-Ньютона устанавливал различимость состояния покоя и состояния движения тела в различное время существования тела: в одно время тело находится в состоянии покоя, в другое время это же тело находится в состоянии равномерного прямолинейного движения. Короче, движение не есть покой, покой не есть движение.
Другой закон, названный принципом относительности Галилея устанавливал:
| состояние покоя тела и состояние его поступательного, равномерного и прямолинейного движения различить невозможно. |
Из него следовало, что поступательное, равномерное и прямолинейное движение Земли в целом не оказывает никакого влияния на физические процессы, происходящие внутри и на земной поверхности, никакими механическими экспериментами, проводимыми внутри инерциальной системы, нельзя определить, покоится она или движется равномерно и прямолинейно. Короче, движение есть покой, покой есть движение.
Может показаться, что принцип относительности Галилея противоречит закону инерции, что один из них является истинным, а другой — ложным.
На самом же деле не отношение закона инерции и принципа относительности заключает в себе противоречие, а отношение состояния покоя к состоянию движения заключает в себе противоречие, которое отражено и выражено отношением закона инерции и принципом относительности Галилея. Закон инерции и принцип относительности вводят теоретическую механику в область диалектики.
Состояние движения и состояние покоя тела являются едиными, имеющими одинаковыми все признаки и неразличимыми. С другой стороны, они имеют различные признаки, являются различимыми и противоположными.
Анализ единства противоположностей требует не только рассмотрения состояния движения тела, не только рассмотрения состояния покоя тела, но ещё и рассмотрения процесса обращения состояния движения в состояние покоя и состояния покоя в состояние движения. Подходящим телом для такого рассмотрения может служить маятник, совершающий гармонические колебания. Колебания маятника можно рассматривать как процесс взаимодействия его внутренних сил: единых и противоположных, друг друга определяющих и друг другу исключающих, т. е. представляющих собой единство противоположностей.
В классической механике инерциальные системы, для которых строго выполняются основные законы Ньютона, находятся на переднем плане, а неинерциальные колебательные системы находятся на заднем плане. В квантовой механике неинерциальные колебательные системы находятся на переднем плане, а инерциальные системы — на заднем плане. Поэтому квантовая механика первоначально называлась волновой механикой.
Знаменитый французский физик Луи де Бройль в 1924 г. выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Прежде было установлено, что фотоны, для которых не существует основной системы отсчёта, обладают корпускулярными и волновыми свойствами. Гипотеза Луи де Бройля устанавливала, что не только фотоны, но и электроны, нейтроны, атомы и молекулы, для которых существуют основные системы отсчёта, обладают корпускулярными и волновыми свойствами. Потом гипотеза де Бройля получила экспериментальное подтверждение и стала собой представлять достоверную научную теорию. Не смотря на это, универсальность корпускулярно-волнового дуализма ограничивалась областью физики микромира.
В статье «Интерпретация волновой механики» (пер с фр. опубликован в журнале «Вопросы философии» №6, 1956г.) Луи де Бройль писал: «Я старался представить себе корпускулу как очень маленькое местное нарушение, включённое в волну, а это привело меня к тому, чтобы рассматривать корпускулу как своего рода маленькие часы, фазы которых всегда должны быть согласованы с фазами той волны, с которой они объединены. Изучая различие между поведением частоты корпускулы-часов и частоты сопровождающей её волны я заметил, что согласование фаз навязывало прямолинейно и равномерно перемещающейся корпускуле совершенно определённое движение по отношению к плоской монохроматической волне, которую мне пришлось с ней ассоциировать»/ «Философские вопросы современной физики». Под ред. И.В. Кузнецова и М.Э. Омельяновского, М., 1958, с. 80/.
В мысленном эксперименте де Бройля движение корпускулы-часов пилотировала волна, игравшая в их взаимодействии активную роль. Корпускула-часы находилась в подчинённом отношении к волне, играла в нём пассивную роль, находилась с волной в одной общей форме, лишалась своих корпускулярных свойств и приобретала волновые свойства. Поэтому в волне она становилась ненаблюдаемой нелокализованной и неуловимой.
Хотя де Бройль предполагал и ожидал, что корпускула-часы, включённые в волну, обнаружат себя в определённом месте волны «как очень маленькое местное нарушение», но его предположение и ожидание не подтвердились.
Волна не вкушает корпускулу, как уж лягушку, которая расширяет его желудок и образует в определённом месте его тела наблюдаемое местное нарушение. Де Бройлю пришлось искать корпускулу в волне с помощью двойного решения уравнения волны и уравнения корпускулы-часов. Значения волновой функции показывали де Бройлю, что в очень маленькой области, в центре её, имеется математическая сингулярность с бесконечным значением. Его происхождение было неизвестным, а его значение — лишённым смысла. Поэтому оно было заменено большим конечным значением и не было включено в корпускулярно-волновую теорию и в теорию двойного решения.
Так как полученный результат мысленного эксперимента Луи де Бройля остался непонятым и невключённым в теорию, то в эксперимент мною были внесены изменения и дополнения. В частности, корпускула-часы были заменены маятником настенных часов типа ходиков. И не маятник был включён в волну, а волна была включена в маятник. Только лишь эти изменения в мысленном эксперименте Луи де Бройля имели своим следствием распространение универсального корпускулярно-волнового дуализм на все физические тела, состоящие из атомов и молекул.
Можно было сравнивать наблюдаемые гармонические колебания маятника с ненаблюдаемыми гармоническими колебаниями частицы линейного гармонического осциллятора и посредством сравнения установить их взаимно однозначное соответствие. В моём распоряжении оказалась прекрасная параллель, раскрывающая многие тайны. В их числе раскрылась тайна происхождения нулевого уровня энергии линейного гармонического осциллятора. Энергия нулевого уровня оказалась обменной энергией, присутствующей в гармонически колеблющейся частице, но ей не принадлежащей. Линейный гармонически осциллятор оказался нелинейным и открытой физической системой. Маятник тоже оказался не консервативной закрытой колебательной системой, внутри которой ничего не изменяется и не развивается, а открытой физической системой. Взаимодействие маятника и волны оказалось существующим в подчинённом отношении к ненаблюдаемой третьей внешней силе.
Собственное пространство маятника и волны и внешнее пространство сообщаются посредством очень маленькой области, через центр которой в маятник входит извне порция количества движения в одной форме в начале периода колебаний и выходит вовне в другой форме в конце периода. Причём, в один определённый момент времени выходящее во внешнее пространств количество движения завершает период, а входящее во внутреннее пространство количество движения начинает собой новый период.
Эта маленькая область и была обнаружена Луи де Бройлем, в центре которой находилась математическая сингулярность с бесконечным значением. За бесконечным значением волновой функции укрывалось двустороннее движение двух порций количества движения, принадлежащих ненаблюдаемой внешней силе. Количество движения, поступающее в маятник извне, проводит в нём всю свою «жизнь».
С начала и до конца периода проходит «детство», «юность», «молодость», «зрелость», «старость» и «дряхлость» вселённого в маятник количества движения. В конце периода происходит обмен старого количества движения на новое количество движения. Описание акта обмена — дело недалёкого будущего времени.
Теперь рассматривается отношение друг к другу состояния движения и состояния покоя маятника, начиная с его самой простой формы, которая соответствует принципу относительности Галилея.
А). Неразличимые состояние движения и состояния покоя принадлежат телу, существующему в своём времени и пространстве, которые неразличимы. Поэтому можно полагать, что
В). Изменение и развитие формы отношения состояний тела ведёт к тому, что неразличимые состояние движения и состояние покоя становятся различимыми состояниями тела, существующего во времени и пространстве, которые стали различимыми в отношении друг к другу и в отношении к самим себе. Определённое время существования тела отличается от его неопределённого времени. Определённое пространство существования тела отличается от его неопределённого пространства.
Движение маятника от верхнего правого положения через нижнее положение до верхнего левого положения осуществляется за половину периода Т времени, имеющему определённое точное значение. Оно осуществляется на неопределённой изменяющейся длине пространства. Определённое время делимо на определённые делимые моменты времени, а неопределённое время не слагается из неделимых «теперь» /Аристотель/.
Покоящийся маятник в верхнем правом положении, или в верхнем левом положении, существует на определённой длине L пространства неопределённое время. Определённая длина пространства делима на делимые свои части, а неопределённая длина пространства не слагается из неделимых «здесь».
Признаки состояний маятника можно обобщить и выразить в форме математического предложения, которое состоит из условияи из вытекающего из него заключения.
Предложение 1. Если тело находится в состоянии равномерного прямолинейного движения, то оно существует в своём определённом времени и неопределённом линейном пространстве.
Предложение 2, обратное. Если тело существует в определённом времени и неопределённом пространстве, то оно находится равномерного прямолинейного движения.
Наблюдаемое движение маятника не является равномерным и прямолинейным. Но из этого не следует, что маятник не находится в равномерном прямолинейном ненаблюдаемом движении. Если возможно воздействие на маятник и волну ненаблюдаемой внешней силы, то возможно и равномерное прямолинейное ненаблюдаемое движение маятника и волны под командной властью внешней силы.
Предложение 3. Если тело находится в состоянии покоя, то оно существует в определённом линейном пространстве неопределённое время.
Предложение 4, обратное. Если тело существует в определённом линейном пространстве неопределённое время, то оно находится в состоянии покоя.
Маятник обладает постоянным весом Р, Б а взаимодействующая с ним волна обладает переменным весом Р, по закону равенства действия и противодействия. Маятник находится в верхнем крайнем правом, или левом, положении в неустойчивом равновесии в состоянии покоя и невесомости. Переменный вес, присутствуя в веществе маятника, не изменяет его величины ни на один атом. Посредством наложения их друг на друга без взаимного искажения, согласно принципу суперпозиции, постоянный вес маятника как бы подпирается снизу переменным весом волны и приобретает свойство невесомости.
В нижнем крайнем положении маятник пересекает на предельно высокой скорости вертикаль справа налево, или слева направо. На его постоянный вес накладывается сверху переменный вес волны. В результате наложения переменного веса постоянный вес возрастает в два раза.
С). Дальнейшее изменение и развитие отношения состояния движения и состояния покоя приводит к тому, что их различие обращается в их прямую противоположность.
Тело переходит из состояния движения, которое соответствует низшему уровню развития отношения, в состояние покоя, которое соответствует высшему уровню развития отношения. Переход из состояния движения в состояние покоя возможен не раньше, чем закончится время Т состояния движения.
За время Т импульс неоднократно переходит из одной, менее развитой, своей формы в другую, более развитую, форму. Формы импульса следуют одна за другой в строгом порядке. И только последняя форма импульса способна обращаться в первую форму энергии. Обращение импульса в энергию происходит не мгновенно, не за один определённый момент времени, а весь период Т колебаний от первого до последнего его момента.
Другими словами, сколько времени существует импульс и состояние движения тела, столько же времени существует процесс обращения импульса в энергию и столько же времени существует энергия и состояние покоя тела.
Параллельно обращению импульса РТ в энергию РL происходит обращение времени Т в длину L пространства посредством их наложения друг на друга без взаимного искажения. В результате образуется пространственно-временной интервал. Его началом является конец «чистого», незамутнённого пространством, определённого времени. Его концом является начало «чистого», незамутнённого временем, определённого линейного пространства.
В каждом из четырёх математических предложений имеется неразлучная пара или определённого времени и неопределённого пространства тела, или определённого пространства и неопределённого времени тела. Эти пары показывают, что любая физическая система не может находиться в состоянии движения или в состоянии покоя, в которых время и пространство системы одновремённо принимают определённые, точные значения. Это значит, что отношение времени и пространства друг к другу любой физической системы представляет собой соотношение неопределённостей, одним из частных случаев которого является принцип неопределённости, открытый в 1927 г. В. Гейзенбергом. Координата центра инерции системы представляет собой линейное пространство, а импульс, в размерности которого имеется размерность времени, представляет собой время.
Закон всемирного тяготения Ньютона описывает силу тяготения как величину, которая зависит от расстояния, т. е. от длины пространства между взаимодействующими телами, и не зависит от времени.Почему? Ответ на вопрос помогает найти предложение 3. Взаимодействующие тела находятся на определённом расстоянии друг от друга в состоянии покоя. Покоящиеся тела существуют в определённом линейном пространстве неопределённое время, которое не имеет определённого, точного значения. Сила тяготения не может зависеть от неопределённого времени. По этой же причине сила взаимодействия электрических зарядов описывается законом Кулона как величина, которая зависит от расстояния и не зависит от времени. Покоящиеся электрические заряды существуют в определённом линейном пространстве неопределённое время.
Основные уравнения электродинамики — уравнения Максвелла — означают, что вихри электрического и магнитного полей определяются производными по времени и не зависят от значения длины пространства. Почему?
Движущиеся вихри электрического поля определяются производной по времени от магнитного поля, а магнитного поля — производной по времени от электрического поля. Электрические и магнитные вихри существуют определённое время в неопределённом пространстве, которое не имеет определённой длины.
В основе утверждения концепции дальнодействия находится существование вихреобразного движения эфира в определённом времени и неопределённом пространстве, а в основе утверждения принципа близкодействия находится существование взаимодействующих покоящихся тел в определённом линейном пространстве неопределённое время.
Можно было бы поставить ещё и другие вопросы и попытаться найти на них ответы. Но лучше подождать их самостоятельного появления. Тогда и ответы на них возникнут сами собой.
К состоянию движения и к состоянию покоя тела имеют непосредственное отношение знаменитые апории Зенона Элейского
См. статью Отношение движения и покоя в апориях Зенона Элейского
Сила трения
Сила трения: величина, направление
С силой трения вы сталкиваетесь буквально каждую секунду. Каждый раз, когда вы взаимодействуете с любой поверхностью — идете по асфальту, сидите на стуле, пьете чай из чашки — на вас действует сила трения.
Трение — это и есть взаимодействие в плоскости соприкосновения двух поверхностей.
Чтобы перевести трение на язык математики, вводится понятие сила трения.
Сила трения — это величина, которая характеризует процесс трения по величине и направлению.
Измеряется сила трения, как и любая сила — в Ньютонах.
Возникает сила трения по двум причинам:
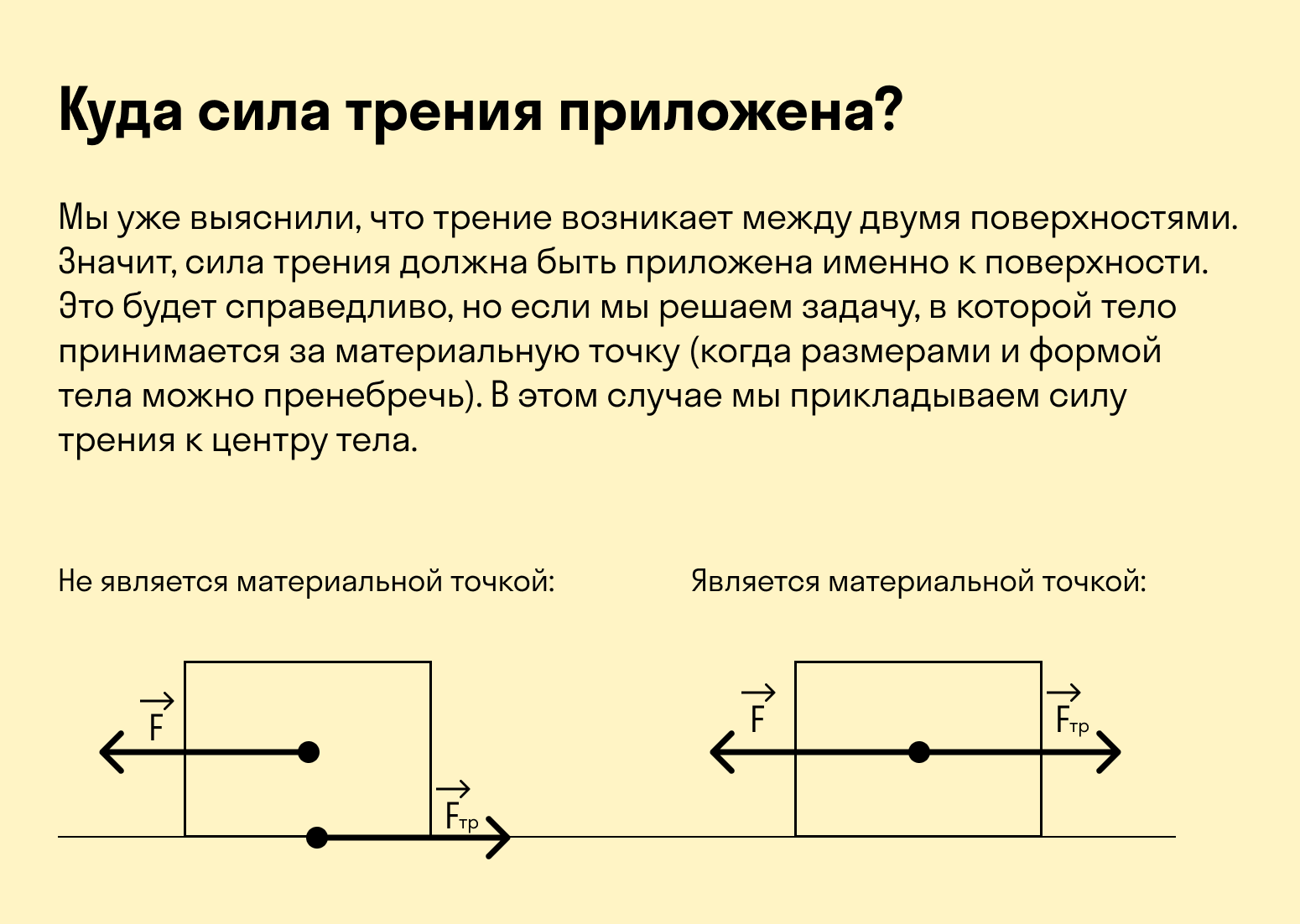
Направлена сила трения всегда против скорости тела. В этом плане все просто, но всегда есть вопрос:
В задачах часто пишут что-то вроде: «Поверхность считать идеально гладкой». Это значит, что сила трения в данной задаче отсутствует. Да, в реальной жизни это невозможно, но во имя красивой математической модели трением часто пренебрегают.
Не переживайте из-за этой несправедливости, а просто решайте задачи без трения, если увидели словосочетание «гладкая поверхность».
Сухое и вязкое трение
Есть очень большая разница между вашим соприкосновением с водой в бассейне во время плавания и соприкосновением между асфальтом и колесами вашего велосипеда.
В случае с плаванием мы имеем дело с вязким трением — явлением сопротивления при движении твердого тела в жидкости или воздухе. Самолет тоже подвергается вязкому трению и вон тот наглый голубь из вашего двора.
А вот сухое трение — это явление сопротивления при соприкосновении двух твердых тел. Например, если школьник ерзает на стуле или злодей из фильма потирает ладоши — это будет сухое трение.
Вязкое трение в школьном курсе физики не рассматривается подробно, а вот сухое — разбирают вдоль и поперек. У сухого трения также есть разновидности, давайте о них поговорим.
Трение покоя
Если вы решите сдвинуть с места грузовик, вряд ли у вас это получится. Не то, чтобы мы в вас не верим — просто это невозможно сделать из-за того, что масса человека во много раз меньше массы грузовика, да еще и сила трения мешает это сделать. Мир жесток, что тут поделать.
В случае, когда сила трения есть, но тело не двигается с места, мы имеем дело с силой трения покоя.
Сила трения покоя равна силе тяги. Например, если вы пытаетесь сдвинуть с места санки, действуя на них с силой тяги 10 Н, то сила трения будет равна 10 Н.
Сила трения покоя
Fтр = Fтяги
Fтр — сила трения скольжения [Н]
Задача
Найти силу трения покоя для тела, на которое действуют сила тяги в 4 Н.
Решение:
Тело покоится, значит
Ответ: сила трения равна 4 Н.
Трение скольжения
А теперь давайте скользить на коньках по льду. Каток достаточно гладкий, но, как мы уже выяснили, сила трения все равно будет присутствовать и вычисляться будет по формуле:
Сила трения скольжения
Fтр = μN
Fтр — сила трения скольжения [Н]
μ — коэффициент трения [-]
N — сила реакции опоры [Н]
Сила трения, которую мы получим по этой формуле будет максимально возможной — то есть больше уже никуда.
Сила реакции опоры — это сила, с которой опора действует на тело. Она численно равна силе нормального давления и противоположна по направлению.
Не совсем. Сила нормального давления направлена всегда перпендикулярно поверхности (нормаль — перпендикуляр к поверхности). Вес не обязательно направлен перпендикулярно поверхности.
В рамках школьного курса вес всегда направлен перпендикулярно поверхности, поэтому силу реакции опоры можно численно приравнивать к весу.
Подробнее про вес тела читайте в нашей статье😇
Также, если тело находится на горизонтальной поверхности, сила реакции опоры будет равна силе тяжести: N = mg.
Коэффициент трения — это характеристика поверхности. Он определяется экспериментально, не имеет размерности и показывает, насколько поверхность гладкая — чем больше коэффициент, тем более шероховатая поверхность. Коэффициент трения положителен и чаще всего меньше единицы.
Задача 1
Масса котика, лежащего на столе, составляет 5кг. Коэффициент трения µ=0,2. К коту прилагают внешнюю силу, равную 2,5Н. Какая сила трения при этом возникает?
Решение:
По условию данной задачи невозможно понять, двигается наш котик или нет. Решение о том, приравниваем ли мы к силе тяги силу трения, принять сразу нельзя. В таких случаях нужно все-таки рассчитать по формуле:
Так как котик лежит на горизонтальной поверхности, сила реакции опоры в данном случае равна силе тяжести: N = mg.
Мы получили максимально возможную силу трения. Внешняя сила по условию задачи меньше максимальной. Это значит, что котик находится в покое. Сила трения уравновешивает внешнюю силу. Следовательно, она равняется 2,5Н.
Ответ: возникает сила трения величиной 2,5 Н
Задача 2
Барсук скользит по горизонтальной плоскости. Найти коэффициент трения, если сила трения равна 5 Н, а сила давления тела на плоскость – 20 Н.
Решение:
В данной задаче нам известно, что барсучок скользит. Значит нужно воспользоваться формулой:
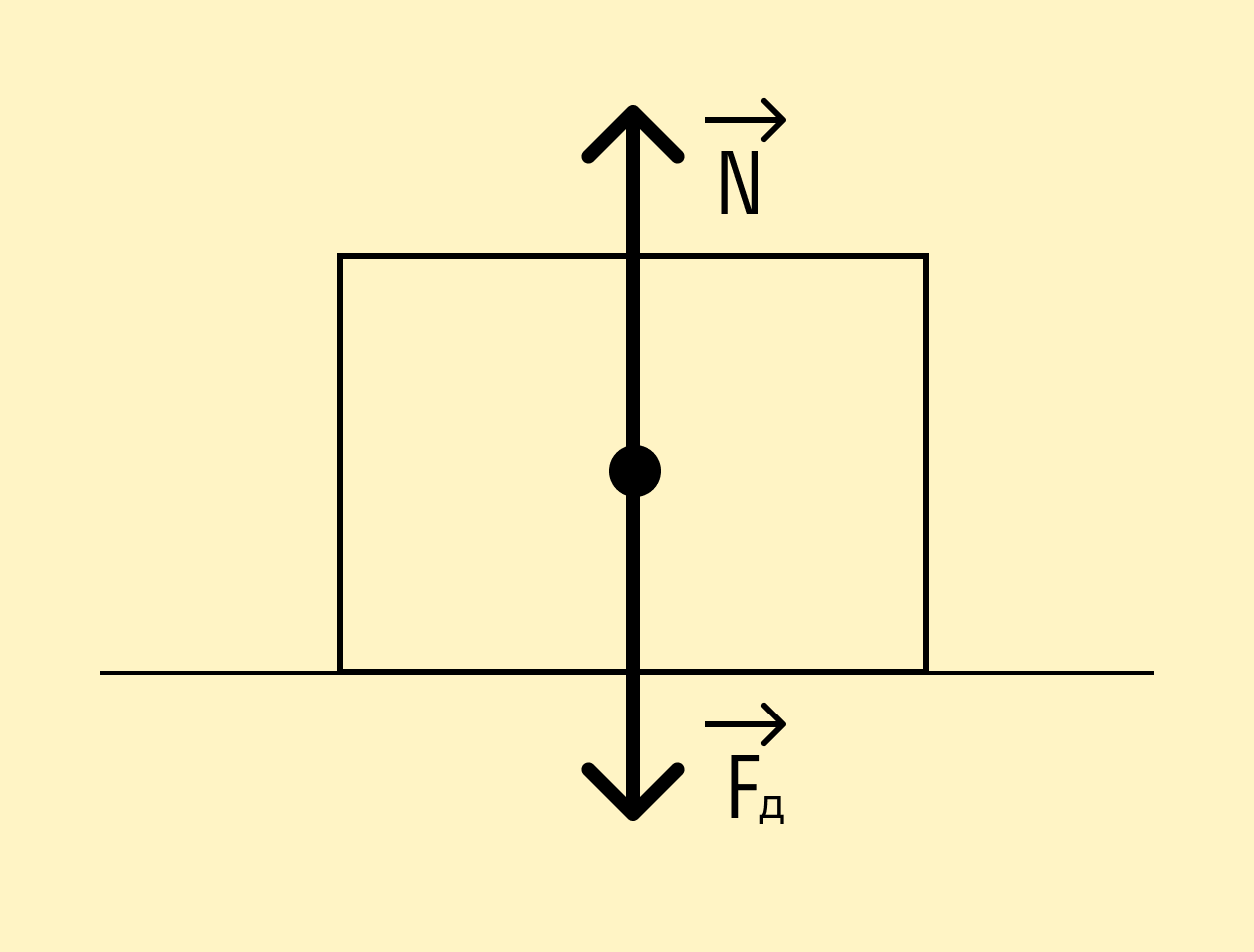
Так как барсук находится на горизонтальной поверхности, сила реакции опоры в данном случае равна силе давления на плоскость: N = Fд.
Выражаем коэффициент трения:
μ = Fтр/Fд = 5/20 = 0,25
Ответ: коэффициент трения равен 0,25
Задача 3
Пудель вашей бабушки массой 5 килограмм скользит по горизонтальной поверхности. Сила трения скольжения равна 20 Н. Найдите силу трения, если пудель сильно похудеет, и его масса уменьшится в два раза, а коэффициент трения останется неизменным.
Решение:
В данной задаче нам известно, что пудель скользит. Значит, нужно воспользоваться формулой:
Так как пудель находится на горизонтальной поверхности, сила реакции опоры в данном случае равна силе тяжести: N = mg.
Выразим коэффициент трения:
μ = Fтр/mg = 20/5*10 = 0,4
Теперь рассчитаем силу трения для массы, меньшей в два раза:
Ответ: сила трения будет равна 10 Н.
Задача 4
Ученик провел эксперимент по изучению силы трения скольжения, перемещая брусок с грузами равномерно по горизонтальным поверхностям с помощью динамометра.
Результаты экспериментальных измерений массы бруска с грузами m, площади соприкосновения бруска и поверхности S и приложенной силы F представлены в таблице.