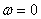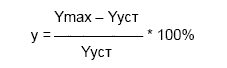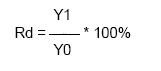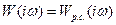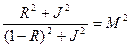Что такое показатель колебательности м

Что такое показатель колебательности м

Оценка качества при гармонических воздействиях

Качество переходных процессов в системах и объектах при гармонических воздействиях оценивают по частотным характеристикам, снятым экспериментально или рассчитанным по параметрам математической модели. В этом случае получают частотные критерии качества переходных процессов, которые относят к косвенным критериям.

Частотные критерии определяют по одной из частотных характеристик: амплитудно-фазовой, амплитудной, вещественной или логарифмической амплитудной. Рассмотрим в качестве основы определение косвенных показателей качества по амплитудной частотной характеристике (АЧХ) систем.

– показатель колебательности, определяемый как отношение максимального значения АЧХ к ее значению при

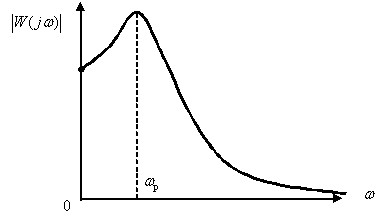
Показатель колебательности характеризует склонность систем или объектов к колебательности. Чем выше показатель колебательности, тем более колебательна система, то есть менее качественна.

При переходная характеристика системы неколебательная, а АЧХ системы имеет примерный вид, показанный на рис. 2.

Если , то говорят о незатухающих колебаниях переходной характеристики, а АЧХ системы имеет вид, показанный на рис. 3.

Считается допустимым, если .

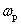
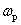
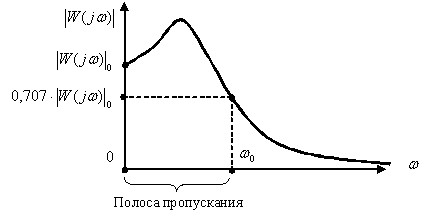
– резонансная частота системы или объекта, при которой АЧХ имеет максимум.

При гармонические сигналы проходят через систему с наибольшим усилением.

Полоса пропускания системы управления – это интервал частот от до частоты , в котором выполняется условие

.

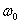
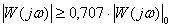
Полоса пропускания систем не должна быть очень широкой, чтобы не проходили высокочастотные помехи. С другой стороны, чем выше частота сигналов, которые пропускает система, тем выше ее быстродействие. 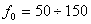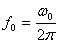В электроприводах полосу пропускания задают в герцах, для систем управления скоростью вращения двигателя полоса пропускания, в зависимости от типа двигателя и преобразователя энергии, находится в диапазоне Гц,

,

при этом накладывается дополнительное ограничение о том, что фазочастотная характеристика в полосе пропускания не должна опускаться ниже .

– частота среза, при которой АЧХ системы принимает значение, равное единице

,

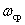
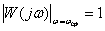
как это показано на рис. 5.

косвенно характеризует длительность переходного процесса, так же как и . Время регулирования системы обратно пропорционально частоте среза –

,

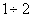
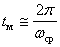
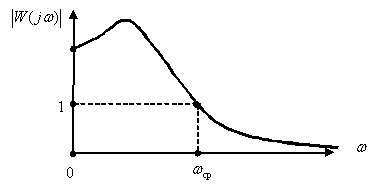
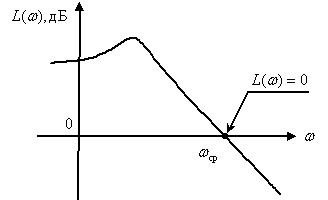
если переходный процесс имеет колебания, то можно установить связь между частотой среза т временем достижения первого максимума –

.

Полоса среза, как характеристика быстродействия систем получила распространение, так как она легко определяется на логарифмических частотных характеристиках (см. рис. 6).

Интегральные оценки качества

Интегральными оценками качества переходного процесса систем управления называют интегралы по времени от некоторых функций переходного процесса изменения ошибки регулирования.

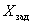
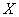
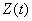
Рассмотрим скалярную линейную систему, показанную на рис. 7. На вход управления системы поступает ступенчатый сигнал с амплитудой , система предназначена для стабилизации заданного значения регулируемой переменной , на систему так же может действовать скалярное ступенчатое возмущение стремящееся снизить значение регулируемой переменной.

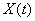
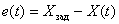
Примерный вид графиков переходных процессов регулируемой величины и ошибки регулирования –

,

показаны соответственно на рис. 8 и 9.

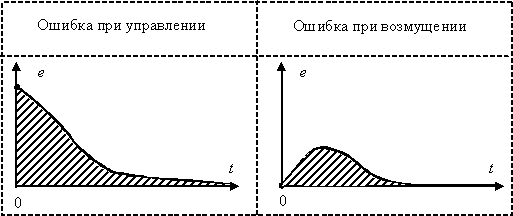
Основные области применения интегральных оценок в теории автоматического управления:

Общая оценка быстроты затухания и величины отклонения регулируемой величины в совокупности, без определения того и другого в отдельности.

Выбор при синтезе параметров систем, обеспечивающих оптимальность переходного процесса с точки зрения достижения минимума интегральных оценок.

Простейшей интегральной оценкой может служить линейная интегральная оценка следующего вида –

.

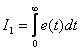
Геометрическая интерпретация этого интеграла представляет собой площадь под кривой 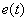, как это показано на рис. 10 для переходных процессов изменения ошибки при управлении и возмущении.

Если система управления устойчива и обладает свойством астатизма, тогда

,

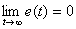
а интеграл стремится к конечному значению, равному площади под кривой . Параметры системы управления стремятся выбирать таким образом, чтобы добиться минимума , при этом идеальный переходный процесс будет стремиться к идеальной ступенчатой форма.

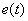
Контрольные вопросы и задачи

Как определить показатель колебательности по АЧХ системы?

Как определить частоту среза и полосу пропускания по АЧХ?

Как соотносятся частота среза системы и ее быстродействие?

Дайте определение линейной интегральной оценке, укажаите ее достоинства и недостатки.

Почему для интегральных оценок переходного процесса используют график изменения ошибки регулирования?

По графику АЧХ системы

определить показатель колебательности и частоту среза системы.

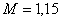
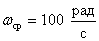
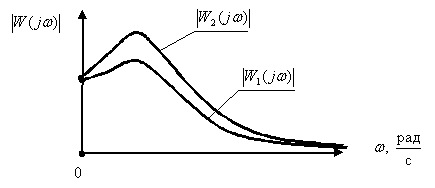
Показатель колебательности , частота среза .

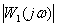
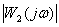
По графикам АЧХ двух систем: САУ1 – , САУ2 – ,

определить систему управления, переходные процессы которой имеют большую колебательность.

Большую колебательность переходных процессов имеет система САУ2.

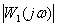
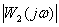
По графикам АЧХ двух систем: САУ1 – , САУ2 – ,

определить систему управления, которая имеет большее быстродействие.

Большую колебательность переходных процессов имеет система САУ1.

Источник

Показатель колебательности М.

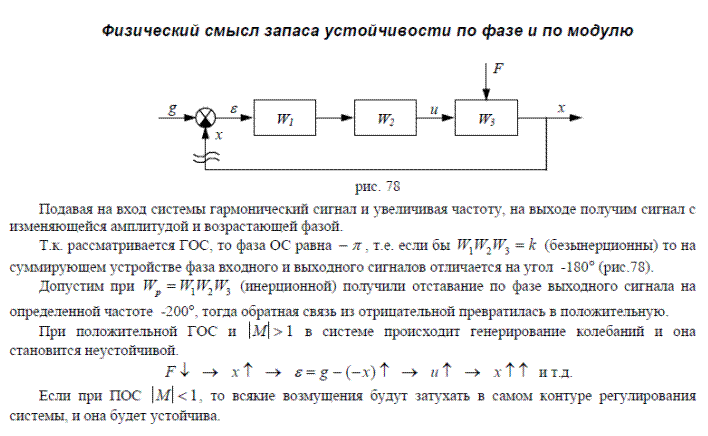
Запас устойчивости по модулю и фазе. Показатель колебательности.

Понятие запаса устойчивости по фазе и по модулю

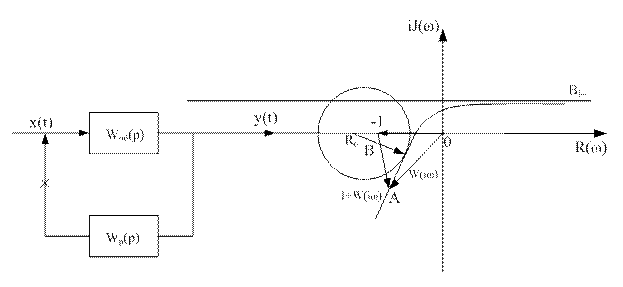
Т.к. параметры системы определяются приближенно и в процессе работы не остаются постоянными, то весьма важное значение имеет оценка удаления частотной характеристики от точки −1,j0. Это удаление характеризует запас устойчивости по фазе и запас устойчивости по модулю (усилению).

За критическую фазу принимается и модуль ϕ=−180οM=1. Для определения этих запасов на частотной характеристике разомкнутой системы проводится окружность радиусом 1 с центром в начале координат (рис.76). Тогда:

Показатель колебательности М.

Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. в этом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность в системе возрастает.

В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.

Источник

Большая Энциклопедия Нефти и Газа

Показатель колебательности М может быть определен и в случае использования логарифмических частотных характеристик. Для этого предварительно рассмотрим условия, которым должны удовлетворять отдельно амплитудная А ( ш) W ( / ш) и фазовая я) ( ш) arg W ( / u) частотные характеристики, для того чтобы а.ф.х. разомкнутой системы не заходила внутрь запретной зоны. [1]

Показатель колебательности М, так же как и степень затухания г з, является мерой устойчивости систем автоматического регулирования, и они тесно связаны между собой. [2]

Показатель колебательности широко используется при синтезе А СР. [4]

Показатель колебательности М, рассмотренный выше, характеризует свойства АСР по задающему воздействию и болыае пригоден для оценки качества следящих систем. [6]

Показатель колебательности М связан со степенью колебательности т и степенью затухания р ( см. гл. [7]

Показатель колебательности М и резонансная частота / т легко измеряются в реальной системе и, следовательно, могут быть полезны как практическое средство проверки выполненных на бумаге расчетов. Простого соотношения между Мп при резонансе и В или t не существует. Уравнение (2.34) в общем случае не справедливо, так как выведено для системы с одной парой полюсов. [8]

Показатель колебательности может быть определен из амплитудной частотной характеристики замкнутой системы или путем построений совместно с амплитудно-фазовой характеристикой разомкнутой системы. По амплитудно-фазовым характеристикам разомкнутой системы производится проверка устойчивости и определение качественных показателей работы замкнутой системы. [10]

Показатель колебательности служит для оценки качества по относительной величине максимума М амплитудой характеристики замкнутой системы ( фиг. [11]

Показатель колебательности легко выразить через передаточную функцию. Действительно, амплитудная характеристика замкнутой системы представляет собой модуль ее передаточной функции. [12]

Показатель колебательности характеризует собой склонность системы к колебаниям. [13]

Показателем колебательности называется максимальное значение модуля амплитудно-частотной характеристики замкнутой системы. В ряде случаев амплитудно-частотная характеристика системы имеет пик при некоторой частоте сор. Показатель колебательности представляет собой, таким образом, наибольшее отношение амплитуды выходного колебания к амплитуде входного. В эти режимах М служит прямым качественным критерием, имеющим ясный и глубокий физический смысл. [14]

Чтобы показатель колебательности был не больше заданного значения, ФЧХ не должна заходить в запретную зону по устойчивости. [15]

Источник

Показатели качества процесса управления

К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.

Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).

Классификация показателей качества состоит из нескольких групп:

Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:

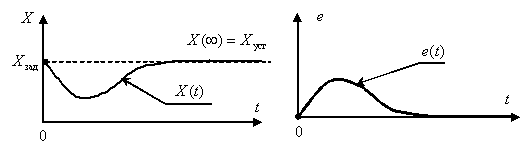
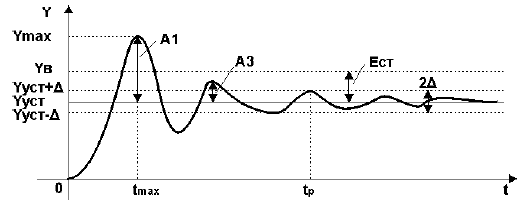
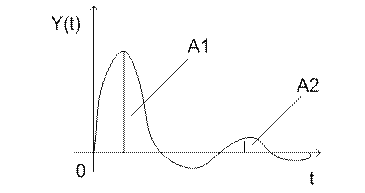
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.

Установившееся значение выходной величины Yуст

Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.

Степень затухания ?

Степень затухания ? определяется по формуле:

Время достижения первого максимума tmax

Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.

Время регулирования tp

Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.

В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.

Ошибка регулирования Ест

Перерегулирование у

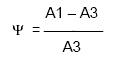
Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:

где значения величин Ymax и Yуст определяются согласно рис.1.

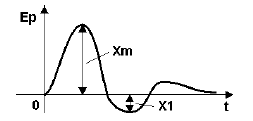
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:

где значения величин Xm и X1 определяются согласно рис. 2.

Динамический коэффициент регулирования Rd

Динамический коэффициент регулирования Rd определяется из формулы:

где значения величин Y1 и Y0 определяются согласно рис. 3.

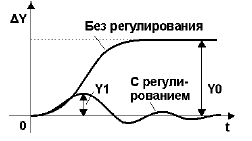
Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.

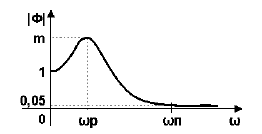
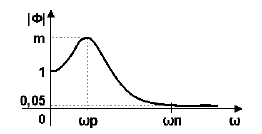
Показатель колебательности М

Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.

Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.

В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.

Источник

Лекция № 14. Устойчивость. Показатель колебательности

Устойчивость. Показатель колебательности.

В частотной области устойчивость оценивается по степени ИЧХ (характ-к) от опасной точки (-1; i0).

На АЧХ это отображается величиной её максимума

Предположим, имеется одноконтурная система, в которой имеется объект и регулятор.

Разомкнем эту систему в какой-то точке. Запишем:

Тогда:

В результате анализа и оценки прохождения годографа вблизи или на большом удалении от опасной точки меняется степень устойчивости.

Вывод:Если ИЧХ разомкн., система проходит далеко от опасной точки, то длина отрезка ВА будет все время больше ОА. И при ω→∞ ВА→1, а ОА→0.

Поэтому на АЧХ это отражается кривой 1.

3 –граничный случай–система находится на границе устойчивости.

Из этих 3-х случаев можно сделать вывод:

Чем больше максимум АЧХ разомкн.системы, тем ближе ИЧХ разомкн.системы проходит к опасной точке (-1; i0), а значит имеет меньший запас устойчивости.

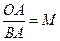
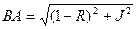
Обозначим: — показатель колебательности

, отсюда

Преобразуем это уравнение относительно переменной R. Тогда получим квадратное уравнение:

Данное уравнение является уравнением окружности с радиусом , а центр будет находиться в точке .

и W разомкнутой системы имеют общую точку (см. выше). Это означает, что изменяя М можно вывести систему на определенную частоту, в которой структура будет устойчивой.

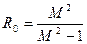
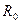
Вывод: Значение амплитуды замкнутой системы при некоторой частоте равно индексу (значению) М окружности, которую пересекает W разомкнутой системы на этой частоте.

Максимум амплитуды наблюдается в точке касания М окружности и W разомкнутой системы. При оценках устойчивости необходимо, чтобы КЧХ разомкнутой системы не заходила внутрь области с радиусом .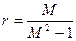

Для практических случаев или же при настройке систем обеспечения запаса устойчивости соответствует М=1,11,6. Это соответствует ψ=0,750,9

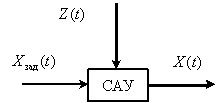
В САУ различают управляющие воздействие и возмущающее воздействие.

Управляющие воздействие должно воспроизводить как можно точнее задание, а на возмущение система должна реагировать как можно меньшими отклонениями регулируемой величины.

Возмущающие воздействия могут быть:

По математическому описанию возмущающие воздействия подразделяются на:

И те и другие воздействия являются функциями времени.

У детерминированных возмущений (функций) их значения заранее известны на любом промежутке времени.

Значения случайных функций на любом интервале времени заранее известны, поэтому случайные возмущения представляют в виде моделей или различного типа числовых характеристик (дисперсия, математическое ожидание, корреляционная функция и тд.).

При оценке работы, САР задаются математическими моделями, которые характеризуют физическую суть данных воздействий.

Одной из таких моделей для промышленных систем регулирования можно определить трехчленную функцию

математическое ожидание, стационарная случайная функция с нулевым математическим ожиданием. Реально данная функция может представляться в виде дифференциального уравнения.

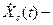
Для промышленных объектов 1 член представляет функцию снормальным распределением (гауссовское распределение) и формируется большим числом независимых друг от друга или слабозависимых факторов.

гармоническая функция

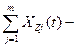
Формируется как результат взаимодействия разнообразных периодических явлений.

сумма самых разнообразных компонентов, имеющих очень низкочастотный характер ( уход со временем от своего заданного значения).

Исход из данного уравнения (модели) можно сделать вывод, что здесь учитывается как статическая непредставительность, так и периодическое воздействие (2 член), связанный с заданными (1 член).

Такой переход к оценке возмущающих воздействий позволяет более точно поддерживать реальную величину с учетом влияния различных возмущений.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник