Что такое побитовые операции
О битовых операциях
Авторизуйтесь
О битовых операциях
В этой статье я расскажу вам о том, как работают битовые операции. С первого взгляда они могут показаться вам чем-то сложным и бесполезным, но на самом деле это совсем не так. В этом я и попытаюсь вас убедить.
Введение
Побитовые операторы проводят операции непосредственно на битах числа, поэтому числа в примерах будут в двоичной системе счисления.
Я расскажу о следующих побитовых операторах:
Битовые операции изучаются в дискретной математике, а также лежат в основе цифровой техники, так как на них основана логика работы логических вентилей — базовых элементов цифровых схем. В дискретной математике, как и в цифровой технике, для описания их работы используются таблицы истинности. Таблицы истинности, как мне кажется, значительно облегчают понимание битовых операций, поэтому я приведу их в этой статье. Их, тем не менее, почти не используют в объяснениях побитовых операторов высокоуровневых языков программирования.
О битовых операторах вам также необходимо знать:
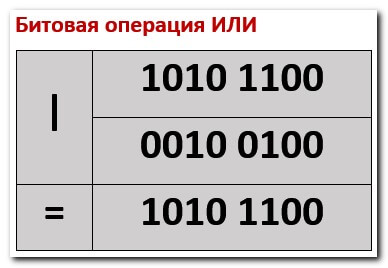
Побитовое ИЛИ (OR)
Побитовое ИЛИ действует эквивалентно логическому ИЛИ, но примененному к каждой паре битов двоичного числа. Двоичный разряд результата равен 0 только тогда, когда оба соответствующих бита в равны 0. Во всех других случаях двоичный результат равен 1. То есть, если у нас есть следующая таблица истинности:
38 | 53 будет таким:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A | B | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
Побитовое И (AND)
Побитовое И — это что-то вроде операции, противоположной побитовому ИЛИ. Двоичный разряд результата равен 1 только тогда, когда оба соответствующих бита операндов равны 1. Другими словами, можно сказать, двоичные разряды получившегося числа — это результат умножения соответствующих битов операнда: 1х1 = 1, 1х0 = 0. Побитовому И соответствует следующая таблица истинности:
Пример работы побитового И на выражении 38 & 53:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A & B | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
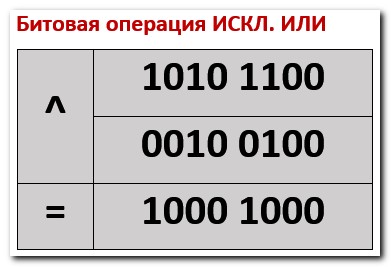
Исключающее ИЛИ (XOR)
Разница между исключающим ИЛИ и побитовым ИЛИ в том, что для получения 1 только один бит в паре может быть 1:
Например, выражение 138^43 будет равно…
| A | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| A ^ B | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
С помощью ^ можно поменять значения двух переменных (имеющих одинаковый тип данных) без использования временной переменной.
Также с помощью исключающего ИЛИ можно зашифровать текст. Для этого нужно лишь итерировать через все символы, и ^ их с символом-ключом. Для более сложного шифра можно использовать строку символов:
Исключающее ИЛИ не самый надежный способ шифровки, но его можно сделать частью шифровального алгоритма.
Побитовое отрицание (NOT)
Побитовое отрицание инвертирует все биты операнда. То есть, то что было 1 станет 0, и наоборот.
Вот, например, операция
Результатом будет 20310
При использовании побитового отрицания знак результата всегда будет противоположен знаку исходного числа (при работе со знаковыми числами). Почему так происходит, узнаете прямо сейчас.
Дополнительный код
Здесь мне стоит рассказать вам немного о способе представления отрицательных целых чисел в ЭВМ, а именно о дополнительном коде (two’s complement). Не вдаваясь в подробности, он нужен для облегчения арифметики двоичных чисел.
Главное, что вам нужно знать о числах, записанных в дополнительном коде — это то, что старший разряд является знаковым. Если он равен 0, то число положительное и совпадает с представлением этого числа в прямом коде, а если 1 — то оно отрицательное. То есть, 10111101 — отрицательное число, а 01000011 — положительное.
Чтобы преобразовать отрицательное число в дополнительный код, нужно инвертировать все биты числа (то есть, по сути, использовать побитовое отрицание) и добавить к результату 1.
Например, если мы имеем 109:
| A | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
A+1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Побитовый сдвиг влево
Побитовые сдвиги немного отличаются от рассмотренных ранее битовых операций. Побитовый сдвиг влево сдвигает биты своего операнда на N количество битов влево, начиная с младшего бита. Пустые места после сдвига заполняются нулями. Происходит это так:
Побитовый сдвиг вправо
Как вы могли догадаться, >> сдвигает биты операнда на обозначенное количество битов вправо.
Если операнд положительный, то пустые места заполняются нулями. Если же изначально мы работаем с отрицательным числом, то все пустые места слева заполняются единицами. Это делается для сохранения знака в соответствии с дополнительным кодом, объясненным ранее.
Вывод
Итак, теперь вы знаете больше о битовых операциях и не боитесь их. Могу предположить, что вы не будете использовать >>1 при каждом делении на 2. Тем не менее, битовые операции неплохо иметь в своем арсенале, и теперь вы сможете воспользоваться ими в случае надобности или же ответить на каверзный вопрос на собеседовании.
Битовые операции
Логические битовые (побитовые) операции
Битовые операции сдвига
В распространённых языках программирования встроенными средствами реализуются только четыре побитовые (битовые) логические операции : И, ИЛИ, НЕ и исключающее ИЛИ. Для задания произвольной побитовой логической операции вполне достаточно перечисленных операций.
И еще, регистр общего назначения (R0. R31) я буду обозначать аббревиатурой РОН.
Битовые (побитовые) логические операции
Битовая операция НЕ:
Если бит равен «1», то после выполнения операции он будет равен «0». И наоборот, если бит равен «0», то после выполнения операции он будет равен «1». (операция выполняется одновременно над всеми битами РОН). В качестве операнда может использоваться только РОН
Обозначается знаком «
Дополнительный код, как и прямой и обратный коды — наиболее распространённые способы представления десятичных чисел в двоичном коде. Это вопрос будет рассмотрен в отдельной статье.
Битовая операция И:
Если оба соответствующих бита операндов равны 1, результирующий двоичный разряд равен 1; если же хотя бы один бит из пары равен 0, результирующий двоичный разряд равен 0. В качестве операндов могут использоваться два РОН или РОН и константа (число, записанное в памяти МК)
Обозначается знаком «&»
Практическое применение:
— для сброса конкретного бита (битов) в ноль:

— для проверки бита на 0 или 1, оно же чтение конкретного бита (если результат равен 0, значит бит равен 0, иначе бит равен 1):
Битовая операция ИЛИ
Если оба соответствующих бита операндов равны 0, двоичный разряд результата равен 0; если же хотя бы один бит из пары равен 1, двоичный разряд результата равен 1. В качестве операндов могут использоваться два РОН или РОН и константа
Обозначается знаком «|» (вертикальная палочка)
Битовая операция ИСКЛЮЧАЮЩЕЕ ИЛИ
Результат действия выполнения операции равен 1, если число складываемых единичных битов нечётно и равен 0, если чётно. В качестве операндов могут использоваться только РОН
Обозначается знаком «^»
Практическое применение:
— для инвертирования битов регистра по маске
Битовые операции сдвига
Логический сдвиг влево
При логическом сдвиге влево происходит сдвиг всех разрядов регистра влево на одну позицию, старший бит (самый левый) при этом теряется, а в младший (самый правый) записывается 0.
Обозначается знаком «
Логический сдвиг вправо
При логическом сдвиге вправо происходит сдвиг всех разрядов регистра вправо на одну позицию, младший бит (самый правый) при этом теряется, а в старший (самый левый) записывается 0
Обозначается знаком «>>»
Логический сдвиг вправо используется как арифметическая операция для целочисленного деления на 2.


Битовые операции
Введение
Я зык Си иногда называют макроассемблером за его тягу к железу. Если не использовать оптимизацию, можно даже примерно оценить, в какие конструкции на ассемблере преобразуется код программы. Простота и минимализм языка (простоту языка не путать с простотой программирования на языке) привели к тому, что на многих платформах си остаётся единственным высокоуровневым языком программирования. Без обзора побитовых операций, конечно, изучения языка было бы неполным.
Побитовые операции, как понятно из названия, позволяют оперировать непосредственно с битами. Большое количество примеров использования побитовых операций можно найти, например, в книге Генри Уоррена «Алгоритмические трюки для программистов». Здесь мы рассмотрим только сами операции и примитивные алгоритмы.
Побитовые И, ИЛИ, НЕ, исключающее ИЛИ
ЗАМЕЧАНИЕ: здесь и далее в примерах используются 8-битные числа для упрощения записи. Всё это верно и для любых других чисел.
Н апомню для начала, что логические операции И, ИЛИ, исключающее ИЛИ и НЕ могут быть описаны с помощью таблиц истинности
| X | Y | X OR Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| X | Y | X XOR Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
В побитовых (bit-wise) операциях значение бита, равное 1, рассматривается как логическая истина, а 0 как ложь. Побитовое И (оператор &) берёт два числа и логически умножает соответствующие биты. Например, если логически умножить 3 на 8, то получим 0
Так как в двоичном виде 3 в виде однобайтного целого представляет собой
Первый бит переменной c равен логическому произведению первого бита числа a и первого бита числа b. И так для каждого бита.
00000011
00001000 ↓↓↓↓↓↓↓↓
00000000
00011111
00010001 ↓↓↓↓↓↓↓↓
00010001
Побитовое произведение чисел 35 и 15 равно 3.
00100011
00001111 ↓↓↓↓↓↓↓↓
00000011
Аналогично работает операция побитового ИЛИ (оператор |), за исключением того, что она логически суммирует соответствующие биты чисел без переноса.
00001111
00001011 ↓↓↓↓↓↓↓↓
00001111
00100001
00001011 ↓↓↓↓↓↓↓↓
00101011
Побитовое отрицание (оператор
) работает не для отдельного бита, а для всего числа целиком. Оператор инверсии меняет ложь на истину, а истину на ложь, для каждого бита. Например,
Исключающее ИЛИ (оператор ^) применяет побитово операцию XOR. Например, для чисел
Иногда логические операторы && и || путают с операторами & и |. Такие ошибки могут существовать в коде достаточно долго, потому что такой код в ряде случаев будет работать. Например, для чисел 1 и 0. Но так как в си истиной является любое ненулевое значение, то побитовое умножение чисел 3 и 4 вернёт 0, хотя логическое умножение должно вернуть истину.
Операции побитового сдвига
О пераций сдвига две – битовый сдвиг влево (оператор >). Битовый сдвиг вправо сдвигает биты числа вправо, дописывая слева нули. Битовый сдвиг влево делает противоположное: сдвигает биты влево, дописывая справа нули. Вышедшие за пределы числа биты отбрасываются.
Например, сдвиг числа 5 влево на 2 позиции
Сдвиг числа 19 вправо на 3 позиции
00010011 >> 3 == 00000010
Независимо от архитектуры (big-endian, или little-endian, или middle-endian) числа в двоичном виде представляются слева направо, от более значащего бита к менее значащему. Побитовый сдвиг принимает два операнда – число, над которым необходимо произвести сдвиг, и число бит, на которое необходимо произвести сдвиг.
Так как сдвиг вправо (>>) дописывает слева нули, то для целых чисел операция равносильна целочисленному делению пополам, а сдвиг влево умножению на 2. Произвести битовый сдвиг для числа с плавающей точкой без явного приведения типа нельзя. Это вызвано тем, что для си не определено представление числа с плавающей точкой. Однако можно переместить число типа float в int, затем сдвинуть и вернуть обратно
Но мы, конечно же, получим не 5.0f, а совершенно другое число.
Особенностью операторов сдвига является то, что они могут по-разному вести себя с числами со знаком и без знака, в зависимости от компилятора. Действительно, отрицательное число обычно содержит один бит знака. Когда мы будем производить сдвиг влево, он может пропасть, число станет положительным. Однако, компилятор может сделать так, что сдвиг останется знакопостоянным и будет проходить по другим правилам. То же самое и для сдвига вправо.
В данном случае при первом сдвиге всё работает, как и задумано, потому что число без знака. Во втором случае компилятор VSE2013 оставляет знак. Однако если посмотреть на представление этого числа, как беззнакового, сдвиг происходит по другим правилам, с сохранением самого левого бита. В последней строчке, если привести число со знаком к числу без знака, то произойдёт обычный сдвиг, и мы получим в результате положительное число.
Побитовые операторы и операторы сдвига не изменяют значения числа, возвращая новое. Они также как и арифметические операторы, могут входить в состав сложного присваивания
Примеры
1. Напишем функции, которые позволяют определять и изменять определённый бит числа
Для того, чтобы узнать, какой бит (1 или 0) стоит на позиции n, воспользуемся логическим умножением.
Пусть имеется число 9
Нужно узнать, выставлен ли бит на позиции 3 (начиная с нуля). Для этого умножим его на число, у которого все биты равны нулю, кроме третьего:
00001001 & 00001000 = 00001000
Теперь узнаем значение бита в позиции 6
00001001 & 01000000 = 00000000
Таким образом, если мы получаем ответ, равный нулю, то на искомой позиции находится ноль, иначе единица. Чтобы получить число, состоящее из нулей с одним битом на нужной позиции, сдвинем 1 на нужное число бит влево.
Заметьте, что в функции условие записано так
Потому что без скобок сначала будет вычислено равенство нулю и только потом выполнено умножение.
Функцию можно упростить
Функция, которая выставляет бит на n-й позиции в единицу.
Известно, что логическое сложение любого бита с 1 будет равно 1. Так что для установки n-го бита нужно логически сложить число с таким, у которого все биты, кроме нужного, равны нулю. Как получить такое число, уже рассмотрено.
Функция, которая устанавливает бит на n-й позиции в ноль.
Для этого нужно, чтобы все биты числа, кроме n-го, не изменились. Умножим число на такое, у которого все биты равны единице, кроме бита под номером n. Например
0001011 & 1110111 = 0000011
Чтобы получить такую маску, сначала создадим число с нулями и одной единицей, а потом инвертируем его.
Функция, изменющая значение n-го бита на противоположное.
Для этого воспользуемся функцией исключающего или: применим операцию XOR к числу, которое состоит из одних нулей и одной единицы на месте нужного бита.
Битовые флаги
Расммотрим синтетический пример. Пусть у нас есть три логические переменные, и нам нужно вывести определённое значение в зависимости от всех этих переменных сразу. Очевидно, что может быть 2 3 возможных вариантов. Запишем это условие в виде ветвления:
Мы получили 8 ветвей. Пусть теперь нам понадобилось добавить ещё одно условие. Тогда число ветвей удвоится, и программа станет ещё сложней для понимания и отладки. Перепишем пример.
Если каждое из наших логичесих значений сдвинуть на своё число бит влево и логически сложить, то мы получим свою уникальную комбинацию бит в зависимоти от значений a, b и c:
Используем этот подход к нашей задаче и заменим ветвеление на switch:
Этот метод очень часто используется для назначения опций функций в разных языках программирования. Каждый флаг принимает своё уникальное название, а их совместное значение как логическая сумма всех используемых флагов. Например, библиотека fcntl:
Здесь флаг O_RDWR рaвен
00000000000000000000001000000000
и O_APPEND
Битовые операции
Данный урок основан на оригинальном уроке по битовым операциям от Arduino, можете почитать его здесь – там всё описано чуть более подробно.
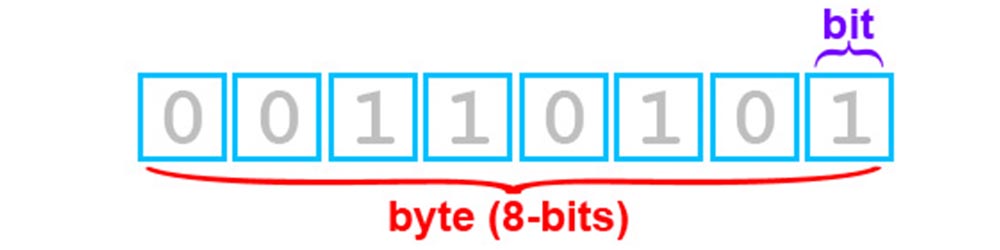
Двоичная система и хранение данных
| 2 в степени | DEC | BIN |
| 0 | 1 | 0b00000001 |
| 1 | 2 | 0b00000010 |
| 2 | 4 | 0b00000100 |
| 3 | 8 | 0b00001000 |
| 4 | 16 | 0b00010000 |
| 5 | 32 | 0b00100000 |
| 6 | 64 | 0b01000000 |
| 7 | 128 | 0b10000000 |
Таким образом, степень двойки явно “указывает” на номер бита в байте, считая справа налево (примечание: в других архитектурах может быть иначе). Напомню, что абсолютно неважно, в какой системе исчисления вы работаете – микроконтроллеру всё равно и он во всём видит единицы и нули. Если “сложить” полный байт в десятичном представлении битов, то мы получим как раз 255: 128+64+32+16+8+4+2+1 = 255. Нетрудно догадаться, что число 0b11000000 равно 128+64, то есть 192. Именно таким образом и получается весь диапазон от 0 до 255, который умещается в один байт. Если взять два байта – будет всё то же самое, просто ячеек будет 16, то же самое для 4 байт – 32 ячейки с единицами и нулями, каждая имеет свой номер согласно степени двойки. Давайте начнём манипуляции с битами с самого простого – с макро-функций, которые идут “в комплекте” с ядром Arduino.
Макросы для манипуляций с битами
В “библиотеке” Arduino.h есть несколько удобных макросов, которые позволяют включать и выключать биты в байте:
| Макросы Arduino.h | Действие |
| bitRead(value, bit) | Читает бит под номером bit в числе value |
| bitSet(value, bit) | Включает (ставит 1) бит под номером bit в числе value |
| bitClear(value, bit) | Выключает (ставит 0) бит под номером bit в числе value |
| bitWrite(value, bit, bitvalue) | Ставит бит под номером bit в состояние bitvalue (0 или 1) в числе value |
| bit(bit) | Возвращает 2 в степени bit |
| Другие встроенные макросы | |
| _BV(bit) | Возвращает 2 в степени bit |
| bit_is_set(value, bit) | Проверка на включенность (1) бита bit в числе value |
| bit_is_clear(value, bit) | Проверка на выключенность (0) бита bit в числе value |
Битовые операции
Переходим к более сложным вещам. На самом деле они максимально просты для микроконтроллера, настолько просты, что выполняются за один такт. При частоте 16 МГц (большинство плат Arduino) одна операция занимает 0.0625 микросекунды.
Битовое И
И (AND), оно же “логическое умножение”, выполняется оператором & или and и возвращает следующее:
Основное применение операции И – битовая маска. Позволяет “взять” из байта только указанные биты:
То есть при помощи & мы взяли из байта 0b11001100 только биты 10000111, а именно – 0b11001100, и получили 0b10000100 Также можно использовать составной оператор &=
Битовое ИЛИ
ИЛИ (OR), оно же “логическое сложение”, выполняется оператором | или or и возвращает следующее:
Основное применение операции ИЛИ – установка бита в байте:
Также можно использовать составной оператор |=
Вы уже поняли, что указывать на нужные биты можно любым удобным способом: в бинарном виде (0b00000001 – нулевой бит), в десятичном виде (16 – четвёртый бит) или при помощи макросов bit() или _BV() ( bit(7) даёт 128 или 0b10000000, _BV(7) делает то же самое)
Битовое НЕ
Битовая операция НЕ (NOT) выполняется оператором
и просто инвертирует бит:
Также она может инвертировать байт:
Битовое исключающее ИЛИ
Битовая операция исключающее ИЛИ (XOR) выполняется оператором ^ или xor и делает следующее:
Данная операция обычно используется для инвертирования состояния отдельного бита:
То есть мы взяли бит №7 в байте 0b11001100 и перевернули его в 0, получилось 0b01001100, остальные биты не трогали.
Битовый сдвиг
Битовый сдвиг делает не что иное, как умножает или делит байт на 2 в степени. Да, это операция деления, выполняющаяся за один такт процессора! К этому мы ещё вернёмся ниже. Посмотрите на работу оператора сдвига и сравните её с макросами bit() и _BV() :
Включаем-выключаем
Вспомним пример из пункта про битовое ИЛИ, про установку нужного бита. Вот эти варианты кода делают одно и то же:
Как насчёт установки нескольких бит сразу?
Или прицельного выключения бит? Тут чуть по-другому, используя &= и
Выключить несколько бит сразу? Пожалуйста!
Именно такие конструкции встречаются в коде высокого уровня и библиотеках, именно так производится работа с регистрами микроконтроллера. Вернёмся к устройству Ардуиновских макросов:
Я думаю, комментарии излишни: макросы состоят из тех же элементарных битовых операций и сдвигов!
Быстрые вычисления
Как я уже говорил, битовые операции – самые быстрые. Если требуется максимальная скорость вычислений – их можно оптимизировать и подогнать под “степени двойки”, но иногда компилятор делает это сам, подробнее смотри в уроке про оптимизацию кода. Рассмотрим базовые операции:
Примечание: рассмотренные выше операции работают только с целочисленными типами данных!
Экономия памяти
При помощи битовых операций можно экономить немного памяти, пакуя данные в блоки. Например, переменная типа boolean занимает в памяти 8 бит, хотя принимает только 0 и 1. В один байт можно запаковать 8 логических переменных, например вот так:
Ещё интересный пример сжатия
Таким образом мы отбросили у красного и синего младшие (правые) биты, в этом и заключается сжатие. Чем больше битов отброшено – тем менее точно получится “разжать” число. Например сжимали число 0b10101010 (170 в десятичной) на три бита, при сжатии получили 0b10101000, т.е. потеряли три младших бита, и в десятичной уже получится 168. Для упаковки используется битовый сдвиг и маска, таким образом мы берём первые пять битов красного, шесть зелёного и пять синего, и задвигаем на нужные места в результирующей 16-битной переменной. Всё, цвет сжат и его можно хранить. Для распаковки используется обратная операция: выбираем при помощи маски нужные биты и сдвигаем их обратно в байт:
Как и в примере со светодиодами, мы просто брали нужные биты ( в этом случае младшие два, 0b11 ) и сдвигали их на нужное расстояние. Для распаковки делаем в обратном порядке:
И получим обратно наши байты. Также маску можно заменить на более удобную для работы запись, задвинув 0b11 на нужное расстояние:
Ну и теперь, проследив закономерность, можно сделать для себя функцию или макрос чтения пакета:
Где x это пакет, а y – порядковый номер запакованного значения. Выведем посмотрим:
“Трюки” с битами
На битовых операциях можно сделать очень много всего интересного, и работать оно будет очень быстро и занимать мало места. Огромный список битовых трюков и хаков можно посмотреть в этой статье, их там очень много и все с примерами. Есть ещё один небольшой сборник самых простых и полезных хаков вот здесь (английский). Его я перевёл, смотрите ниже под спойлером. Другой вариант перевода (могут быть не все трюки) можно посмотреть здесь.
Перемотка бита
Целые
Установка n го бита
Выключение n го бита
Инверсия n го бита
Округление до ближайшей степени двойки
Округление вниз
Получение максимального целого
Получение минимального целого
Получение максимального long
Умножение на 2
Деление на 2
Умножение на m ую степень двойки
Деление на m ую степень двойки
Остаток от деления
Проверка равенства
Проверка на чётность (кратность 2)
Обмен значениями
Получение абсолютного значения
Максимум из двух
Минимум из двух
Проверка на одинаковый знак
Смена знака
Вернёт 2 n
Является ли число степенью 2
Остаток от деления на 2 n на m
Среднее арифметическое
Получить m ый бит из n (от младшего к старшему)
Получить m ый бит из n (от старшего к младшему)
Проверить включен ли n ый бит
Выделение самого правого включенного бита
Выделение самого правого выключенного бита
Выделение правого включенного бита
Выделение правого выключенного бита
n + 1
n – 1
Получение отрицательного значения
if (x == a) x = b; if (x == b) x = a;
Поменять смежные биты
Different rightmost bit of numbers m & n
Common rightmost bit of numbers m & n
Десятичные дроби
Примечание: хаки с float могут не работать на Ардуино! Разбить float в массив бит (unsigned uint32_t)
Вернуть массив бит обратно в float
Быстрый обратный квадратный корень
Быстрый n ый корень из целого числа
Быстрая степень
Быстрый натуральный логарифм
Быстрая экспонента
Строки
Конвертировать в нижний регистр
Конвертировать в верхний регистр
Инвертировать регистр
Позиция буквы в алфавите (англ)
Позиция большой буквы в алфавите (англ)
Позиция строчной буквы в алфавите (англ)
Другое
Быстрая конвертация цвета R5G5B5 в R8G8B8
Приоритет операций
Чтобы не плодить скобки, нужно знать приоритет операций. В C++ он такой: