Что такое плоская фигура

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
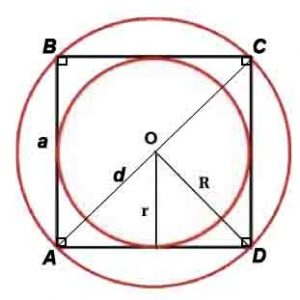
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
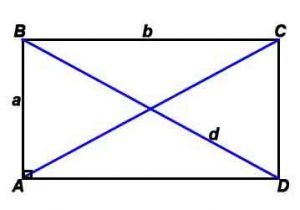
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).

Свойства:

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
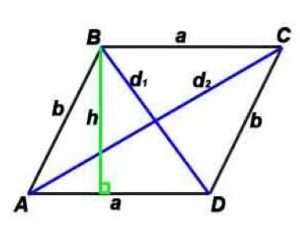
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства:

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α

Свойства:

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)

Свойства:

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4

где π = 3,14 (3,1415926535) – величина постоянная,
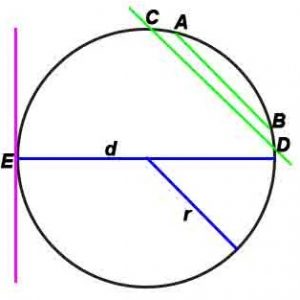
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Источник

Плоская фигура

Плоская фигура — связное замкнутое подмножество , ограниченное конечным числом попарно не пересекающихся жордановых кривых.

Многоугольная фигура

В случае, если все входящие в состав границы плоской фигуры кривые являются ломаными, то фигура называется многоугольной фигурой. Односвязная многоугольная фигура является многоугольником.

Литература

Смотреть что такое «Плоская фигура» в других словарях:

фигура — ы, ж. figure f., нем. Figure <, лат. figura внешний вид, образ. 1. устар. Форма, очертание чего л. БАС 1. А как те палаты сделаны и то дисение покажем в тетрате той о всяких фигурах. АК 1 124. Фигуры. Начертания. Кантемир Соч. 2 421. Какою же… … Исторический словарь галлицизмов русского языка

ФИГУРА — (лат. figura, от fingere лепить, ваять). 1) наружный вид предмета, внешнее очертание. 2) в геометрии: очерк плоскости, чертеж. 3) в картах: туз, король, дама, валет. 4) в риторике: украшение речи, оборот, употребляемый для красоты слога. 5) в… … Словарь иностранных слов русского языка

Фигура постоянной ширины — Треугольник Рело. Кривая постоянной ширины a плоская выпуклая кривая, длинa ортогональной проекции которой на любую прямую равна a. Иными словами, кривой постоянной ширины называется плоская выпуклая кривая, расстояние между любыми двумя… … Википедия

Фигура (шахматы) — Шахматы шахматные часы, шахматная доска, начальная расстановка шахматных фигур Количество игроков 2 Диапазон возрастов 5+ Время установки Обычно 10 60 секунд Длительность партии 10 секунд 7 часов * Сложность правил … Википедия

Звезда (геометрическая фигура) — Правильная четырёхконечная звезда Звезда определённый вид плоских невыпуклых многоугольников, не имеющий однако однозначного математического определения. Обычно под звёздами подразумевают фигуры, напоминающие по форме изображение звезды. Одно из … Википедия

круг — ▲ плоская фигура ↑ внутри, окружность круг область (плоская фигура), ограниченная окружностью. в радиусе каком … Идеографический словарь русского языка

полоса — ▲ плоская фигура ↑ имеющий, постоянный, ширина полоса протяженная плоская фигура постоянной ширины. полосовой (# железо). лента (# шоссе). ленточный. дорожка. ▼ кайма, берег, дорога … Идеографический словарь русского языка

Симметрия — I Симметрия (от греч. symmetria соразмерность) в математике, 1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости α в пространстве (относительно прямой а на плоскости), преобразование пространства… … Большая советская энциклопедия

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

Симметрия (в математике) — Симметрия (от греч. symmetria ‒ соразмерность) в математике, 1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости a в пространстве (относительно прямой а на плоскости), ‒ преобразование пространства (плоскости), при… … Большая советская энциклопедия

Источник

Геометрические фигуры плоские и объёмные

Цели урока:

Планируемые результаты:

личностные:

метапредметные:

предметные:

УУД общенаучные:

УУД личностные:

Тип урока: изучение нового материала.

Методы: словесные, исследовательские, наглядные, практические.

Формы работы: фронтальная, групповая, парная, индивидуальная.

1. Организация начала урока.

Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!

2. Актуализация знаний.

Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!

Чтобы дойти до цели, надо прежде всего идти.

Перед вами высказывание, прочитайте. Что означает это высказывание?

(Чтобы чего-то добиться, нужно что-то делать)

— И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.

— Начнем наш путь к достижению цели сегодняшнего урока.

3. Подготовительная работа.

— Посмотрите на экран. Что вы видите? (Геометрические фигуры)

Назовите эти фигуры.

— Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)

— У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.

— По какому признаку вы разделили эти фигуры?

— С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?

— Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)

— Чему мы должны научиться на уроке?

4. «Открытие» нового знания в практической исследовательской работе.

(Учитель показывает куб и квадрат.)

— Можно ли сказать, что это одно и тоже?

— Чем же отличается куб от квадрата?

— Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)

— Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?

! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)

— Можно ли куб полностью (весь) прижать к парте? Проверим.

— Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?

! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)

ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)

Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.

4. Открытие новых знаний.

1. Назовите фигуры, изображенные на рисунке.

— Какую форму имеют основания этих фигур?

— Какие еще формы можно увидеть на поверхности куба и призмы?

2. Фигуры и линии на поверхности объемных фигур имеют свои названия.

— Предложите свои названия.

— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.

— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.

Работа с тетрадями: чтение нового материала

Соотнесение реальных объектов и объёмных тел.

— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.

5. Физминутка.

1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.

(Ученики «обхватывают» руками и гладят воображаемый шар.)

А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.

Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.

Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!

6. Групповая работа:

(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 1. (Для изучения параллелепипеда)

Группа 2. (Для изучения пирамиды)

Группа 3. (Для изучения куба)

Далее каждая группа выступает, представляя свою объемную фигуру другим.

7. Решение кроссворда

8. Итог урока. Рефлексия деятельности.

Решение кроссворда в презентации

— Что нового вы для себя сегодня открыли?

+ Все геометрические фигуры можно разделить на объёмные и плоские.

Источник

Плоские геометрические фигуры, 2 класс

Описание презентации по отдельным слайдам:

Геометрические фигуры Плоские Объёмные

Линия Замкнутая Разомкнутая её начало и конец находятся в одной точке. её начало и конец не соединены

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками. А В

Круг — часть плоскости, ограниченная окружностью.

Овал — замкнутая выпуклая гладкая плоская кривая.

Через две точки можно начертить неограниченное количество кривых, но только одну прямую. А В А В

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков ВЕРШИНЫ ЗВЕНО

Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – его вершиной Прямой Острый Тупой

Многоугольник — это замкнутая ломанная линия

Точки называются вершинами четырехугольника, а соединяющие их отрезки – сторонами.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-076113

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Новые аккредитационные показатели для вузов вступят в силу с 1 марта

Время чтения: 1 минута

ОНФ проверит качество охраны в российских школах

Время чтения: 2 минуты

К 2024 году в каждой российской школе должен появиться спортивный клуб

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Петербургский Политех создал отдельное меню для вегетарианцев в своих столовых

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Математика. 5 класс

Конспект урока

Геометрические фигуры. Геометрические тела

Перечень вопросов, рассматриваемых в теме:

— единицы измерения длины;

— периметр и площадь многоугольника (прямоугольника, квадрата);

— плоские геометрические фигуры;

— объемные геометрические фигуры.

Геометрия – раздел математики, изучающий свойства фигур.

Треугольник – геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки – сторонами треугольника.

Прямоугольник – четырёхугольник, у которого все углы прямые (каждый – 90 градусов).

Квадрат – прямоугольник, у которого все стороны равны.

Плоские фигуры – фигуры, которые можно целиком расположить на одной плоской поверхности.

Периметр многоугольника – сумма длин всех его сторон.

Площадь – часть плоскости, заключённой внутри замкнутой геометрической фигуры.

Единицы измерения длины: миллиметр (мм), сантиметр (см), дециметр (дм), метр (м), километр (км).

Единицы измерения площади – квадратные миллиметры (мм 2 ), квадратные сантиметры (см 2 ), квадратные метры (м 2 ), квадратные километры (км 2 ).

Прямоугольным параллелепипедом называется фигура, в основании которой находится прямоугольник. Фигура имеет шесть граней. Грани, пресекаясь, образовывают ребра, их 12.

Куб – прямоугольный параллелепипед, у которого все грани- равные квадраты.

Теоретический материал для самостоятельного изучения

Мы знаем, что математика делится на несколько разделов. С одним разделом мы уже знакомы – это арифметика. В арифметике мы в основном занимаемся вычислениями, то есть действиями с числами. Ещё один раздел математики – геометрия. Что же такое геометрия? Разобьём слово «геометрия» на части: «гео» и «метрия». Слово «гео» в переводе с древнегреческого означает «земля». Слово «метрия» в переводе с древнегреческого означает «измерение». Следовательно, слово «геометрия» можно перевести как «землемерие».

А теперь давайте вспомним, какие единицы измерения длин нам известны. Если мы едем из одного города в другой, то расстояние, которое мы преодолели, измеряется в километрах. Обозначение километра – км.

Метры используются для измерения меньших расстояний и длин, например, для измерения роста человека. Обозначение метра – буква м.

Есть более маленькие единицы измерения длины – дециметры, сантиметры, миллиметры: все они используются для измерения небольших длин. Обозначение дециметра – дм, сантиметра – см, миллиметра – мм. Например, длина одной стороны шоколадки равна 1 дм, длина спички равна 4 см, длина муравья – 5 мм.

Стоит запомнить следующую информацию:

1 м = 10 дм = 100 см

А теперь вспомним основные геометрические фигуры.

Треугольник состоит из трёх точек и трёх отрезков, которые попарно соединяют эти точки. Точки – это вершины треугольника, а отрезки – его стороны. Вершины треугольника обозначаются заглавными латинскими буквами.

Следующая фигура – прямоугольник. Он уже состоит из четырёх точек и четырёх попарно соединяющих их отрезков, у него все углы прямые. Точки – это вершины прямоугольника, отрезки – стороны.

У прямоугольника две величины – длина и ширина. Вершины прямоугольника обозначаются заглавными латинскими буквами.

Прямоугольник, у которого все стороны равны, называется квадратом.

Треугольник, прямоугольник и квадрат – это многоугольники, так как у них много вершин – углов.

Ещё одна важная геометрическая фигура – круг. Чтобы начертить круг, мы используем циркуль.

Все фигуры, которые мы рассмотрели, плоские, то есть их можно целиком расположить на одной плоской поверхности.

У всех плоских многоугольников можно найти периметр и площадь. Мы знаем, что периметр – это сумма длин всех сторон. Обозначается периметр заглавной латинской буквой Р. Чтобы найти периметр прямоугольника, используют такую формулу:

P = 2 ∙ (а + b), где a – длина, b – ширина.

Чтобы найти периметр квадрата, используют эту формулу:

P = 4 ∙ a, где а – сторона квадрата.

Длина прямоугольника – 6 см, а ширина – 5 см. Найдите периметр прямоугольника.

Решение: чтобы найти периметр данного прямоугольника, воспользуемся формулой. Для этого вместо букв подставим в формулу заданные значения:

P = 2 ∙ (а + b) = 2 ∙ (5 + 6) = 2 ∙ 11 = 22 (см).

Также нам известно, что у прямоугольника и квадрата можно найти площадь, которая обозначается заглавной латинской буквой S. Площадь прямоугольника рассчитывается по следующей формуле:

S = a ∙ b, где a – длина, b – ширина.

Стоит отметить, что площадь измеряется в мм 2 ; см 2 ; м 2 ; км 2 и т. д.

Площадь квадрата находится по формуле:

S = а ∙ а, где а – сторона квадрата.

Найдите площадь участка земли, имеющего форму прямоугольника со сторонами 7 и 15 метров.

Решение: чтобы найти площадь прямоугольного участка, воспользуемся формулой площади прямоугольника. Для этого вместо букв подставим в формулу заданные значения: S = a ∙ b = 7 ∙ 15 = 105 (м 2 ).

Помимо плоских фигур существуют и объёмные фигуры, и вы с ними уже знакомы. Ежедневно они встречаются нам в домах и на улице. Это куб, параллелепипед, шар, пирамида, цилиндр, конус.

Сегодня мы с вами познакомились с одним из разделов математики – геометрией. Повторили единицы измерения длин. Вспомнили основные плоские и объёмные фигуры. Применили формулы вычисления периметра и площади прямоугольника и квадрата.

Нахождение площади прямоугольного треугольника.

Задача. Найдите площадь прямоугольного треугольника, если стороны, которые образуют прямой угол, равны 13 см и 16 см.

Решение: в задаче нам поможет прямоугольник. Давайте начертим фигуру со сторонами 13 см и 16 см.

Затем проведем отрезок, соединяющий две противоположные вершины, – диагональ. Обратите внимание, что диагональ разбивает этот прямоугольник на два равных прямоугольных треугольника.

Найдем площадь прямоугольника:

S = 13 ∙ 16 = 208 (см 2 ).

Так как диагональ разбивает прямоугольник на два равных треугольника, то можно сделать вывод, что и площади этих треугольников равны. Следовательно, площадь одного такого треугольника будет равна половине площади прямоугольника, то есть надо площадь прямоугольника поделить на 2:

S = 208 : 2 = 104 (см 2 ).

Разбор решения заданий тренировочного модуля

№ 1. Периметр треугольника равен 37 см. Одна сторона треугольника равна 10 см, вторая – 17 см. Найдите третью сторону.

Решение: чтобы решить данную задачу, нужно вспомнить определение периметра многоугольника: периметр – это сумма длин всех сторон. Чтобы найти неизвестную сторону надо от периметра отнять известные нам стороны:

Ответ: третья сторона равна 10 см.

Варианты ответов: 18 м; 9 м; 8 м; 16 м.

Решение: чтобы решить эту задачу, следует воспользоваться формулой площади квадрата S = а ∙ а

Нам надо найти такое число, которое при умножении само на себя даст 81. Такое число 9. Следовательно, сторона квадрата будет равна 9 м.

Источник