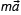Что такое плечо веса
Что такое плечо веса
§ 41. Остойчивость.
Остойчивостью называется способность судна, выведенного из положения нормального равновесия какими-либо внешними силами, возвращаться в свое первоначальное положение после прекращения действия этих сил.
К внешним силам, способным вывести судно из положения нормального равновесия, относятся ветер, волны, перемещение грузов и людей, а также центробежные силы и моменты, возникающие при поворотах судна.
Судоводитель обязан знать особенности своего судна и правильно оценивать факторы, влияющие на его остойчивость. Различают поперечную и продольную остойчивость.
Рис 89 Статические силы, действующие на судно при малых накренениях.
Поперечная остойчивость судна характеризуется взаимным расположением центра тяжести G и центра величины С.
Если судно накренить па один борт на малый угол (5—10°) (рис. 89), ЦВ переместится из точки С в точку С1.
Соответственно сила поддержания, действующая перпендикулярно к поверхности, пересечет диаметральную плоскость (ДП) в точке М.
Точка пересечения ДП судна с продолжением направления силы поддержания при крепе называется начальным метацентром М. Расстояние от точки приложения силы поддержания С до начального метацентра называется метацентрическим радиусом.
Расстояние от начального метацентра М до центра тяжести G называется начальной метацентрической высотой h 0.
Начальная метацентрическая высота характеризует остойчивость при малых наклонениях судна, измеряется в метрах и является критерием начальной остойчивости судна.
Как правило, начальная метацентрическая высота мотолодок и катеров считается хорошей, если она больше 0,5 м, для некоторых судов она допустима меньше, но не менее 0,35 м.
Рекомендуется практически начальную метацентрическую высоту (для килеватых судов) определять следующим приближенным способом.
Рис. 90. Зависимость начальной метацентрической высоты от длины судна
Резким наклонением вызывается поперечная качка судна и секундомером замеряется период свободной качки, т. е. время полного размаха от одного крайнего положения до другого и обратно. Поперечную метацентрическую высоту судна определяют по формуле:
h 0 = 0,525( 
) 2 м,
Т — период качки, сек.
Для оценки полученных результатов служит кривая на рис. 90, построенная по данным удачно спроектированных катеров. Если начальная метацентрическая высота h о, определенная по вышеприведенной формуле, окажется ниже заштрихованной полосы, то означает, что судно будет иметь плавную качку, но недостаточную начальную остойчивость, и плавание на нем может быть опасным.
Если метацентр расположен выше заштрихованной полосы, судно будет отличаться стремительной (резкой) качкой, но повышенной остойчивостью, и следовательно такое судно более мореходно, но обитаемость на нем неудовлетворительна. Оптимальными будут значения, попадающие в зону заштрихованной полосы.
Остойчивость мотолодки и катеров должна выдерживать следующие условия: угол крена полностью укомплектованного судна с мотором от размещения на борту груза, равного 60% установленной грузоподъемности, должен быть меньше угла заливания.
Установленная грузоподъемность судна включает в себя вес пассажиров и вес дополнительного груза (снаряжение, провиант).
Накрененный борт будет вытеснять воды больше, чем противоположный, и ЦВ сместится в сторону крена.
Тогда равнодействующие силы поддержания и веса будут неуравновешенными, образующими пару сил с плечом, равным
Повторное действие сил веса и поддержания измеряется восстанавливающим моментом
Где D — сила плавучести, равная силе веса судна;
l — плечо остойчивости.
Эта формула называется метацентрической формулой остойчивости и справедлива только для малых углов крена, при которых метацентр можно считать постоянным.
При больших углах крена метацентр не является постоянным, вследствие чего нарушается линейная зависимость между восстанавливающим моментом и углами крена.
Взаимным расположением груза на судне судоводитель всегда может найти наиболее выгодное значение метацентрической высоты, при которой судно будет достаточно остойчивым и меньше подвергаться качке.
Кренящим моментом называется произведение веса груза, перемещаемого поперек судна, на плечо, равное расстоянию перемещения. Если человек весом 75 кг, сидящий на банке, переместится поперек судна на 0,5 м, то кренящий момент будет равен 75*0,5 = 37,5 кг/м.
Рис 91. Диаграмма статической остойчивости
Для изменения момента, накреняющего судно па 10°, надо загрузить судно до полного водоизмещения совершенно симметрично относительно диаметральной плоскости.
Загрузку судна следует проверить по осадкам, измеряемым с обоих бортов. Креномер устанавливается строго перпендикулярно диаметральной плоскости таким образом, чтобы он показал 0°.
После этого надо перемещать грузы (например, людей) на заранее размеченные расстояния до тех пор, пока креномер не покажет 10°. Опыт для проверки следует произвести так: накренить судно на один, а затем на другой борт.
Зная крепящие моменты накреняющего судно на различные (до наибольшего возможного) углы, можно построить диаграмму статической остойчивости (рис. 91), что оценит остойчивость судна.
Остойчивость можно увеличивать за счет увеличения ширины судна, понижения ЦТ, устройства кормовых булей.
Если центр тяжести судна расположен ниже центра величины, то судно считается весьма остойчивым, так как сила поддержания при крене не изменяется по величине и направлению, но точка ее приложения смещается в сторону наклона судна (рис. 92, а).
Поэтому при крене образуется пара сил с положительным восстанавливающим моментом, стремящимся вернуть судно в нормальное вертикальное положение па прямой киль. Легко убедиться, что h>0, при этом метацентрическая высота равна 0. Это типично для яхт с тяжелым килем и нетипично для более крупных судов с обычным устройством корпуса.
Если центр тяжести расположен выше центра величины, то возможны три случая остойчивости, которые судоводитель должен хорошо знать.
Первый случай остойчивости.
Метацентрическая высота h>0. Если центр тяжести расположен выше центра величины, то при наклонном положении судна линия действия силы поддержания пересекает диаметральную плоскость выше центра тяжести (рис. 92, б).
Рис. 92. Случай остойчивого судна
В этом случае также образуется пара сил с положительным восстанавливающим моментом. Это типично для большинства судов обычной формы. Остойчивость в этом случае зависит от корпуса и положения центра тяжести по высоте.
При крене кренящийся борт входит в воду и создает дополнительную плавучесть, стремящуюся выровнять судно. Однако при крене судна с жидкими и сыпучими грузами, способными перемещаться в сторону крена, центр тяжести также сместится в сторону крена. Если центр тяжести при крене переместится за отвесную линию, соединяющую центр величины с метацентром, то судно опрокинется.
Второй случай неостойчивого судка при безразличном равновесии.
Метацентрическая высота h = 0. Если центр тяжести лежит выше центра величины, то при крене линия действия силы поддержания проходит через центр тяжести MG = 0 (рис. 93).
В данном случае центр величины всегда располагается на одной вертикали с центром тяжести, поэтому восстанавливающаяся пара сил отсутствует. Без воздействия внешних сил судно не может вернуться в прямое положение.
В данном случае особо опасно и совершенно недопустимо перевозить на судне жидкие и сыпучие грузы: при самой незначительной качке судно перевернется. Это свойственно шлюпкам с круглым шпангоутом.
Третий случай неостойчивого судна при неустойчивом равновесии.
Метацентрическая высота h
Сила тяжести и сила поддержания при малейшем крене образуют пару сил с отрицательным восстанавливающим моментом и судно опрокидывается.
Рис. 93. Случай неостойчивого судна при безразличном равновесии
Рис. 94. Случай неостойчивого судна при неустойчивом равновесии
Разобранные случаи показывают, что судно остойчиво, если метацентр расположен выше центра тяжести судна.
Чем ниже опускается центр тяжести, тем судно более остойчиво. Практически это достигается расположением грузов не на палубе, а в нижних помещениях и трюмах.
Рычаг. Равновесие сил на рычаге
Содержание
С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.
Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.
Рисунок 1. Строительство пирамид по Геродоту (гравюра XVIII века).
В данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.
Устройство рычага
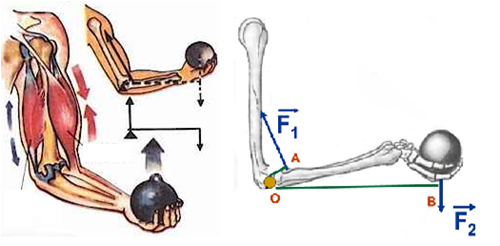
Рычаг – это любое твердое тело, которое может вращаться вокруг неподвижной опоры.
Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.
В обоих случаях у этого рычага есть неподвижная точка опоры – точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.
Сила, с которой Образавр действует на палку (рычаг) меньше веса камня, но, тем не менее, у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.
Таким образом, рычаги бывают двух видов (рисунок 3):
Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.
Условие равновесия рычага
Рисунок 4. Рычаг.
Рисунок 5. Схематическое изображение рычага.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.
С помощью таких опытов было установлено правило равновесия рычага:
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил
Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют – правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: “Дайте мне точку опору, и я переверну Землю!”.
Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.
Примеры задач
Показать решение и ответ
Решение:
Запишем правило равновесия рычага:
$F_1 = F_2 \cdot \frac
СИ:
$0.1 \space кг$
$0.2 \space кг$
$0.5 \space м$
$0.2 \space м$
Показать решение и ответ
$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 \frac<Н> <кг>\cdot (0.1 \space кг + 0.2 \space кг) = 9.8 \frac<Н> <кг>\cdot 0.3 \space кг \approx 3 \space Н$.
Запишем правило равновесия рычага:
Найдем массу груза:
$m_3 = \frac
О массе, силе, весе, рычаге и не только
В 7 классе мы начали изучать физику по УМК Перышкина А.В.
Я спешила познакомиться с этой наукой, потому, что моя мама закончила физический факультет Куйбышевского государственного университета. Она всегда говорит, что физика – это очень интересно и очень увлекательно!
Сейчас я учусь в 9 классе, скоро экзамены. На ОГЭ, кроме математики и русского языка, я выбрала физику. Физика, действительно, очень интересная, увлекательная наука, но и сложная.
В повседневной жизни многие физические понятия используются неверно. Например, очень часто можно услышать: «Мой вес 40 килограмм» или «Этот тортик весит полкило». Но, вес и масса – это два разных понятия! Их нельзя путать.
В учебнике физики Перышкина А.В. за 7 класс в §19 мы найдем определение массы. Масса тела – это физическая величина, которая характеризует его инертность.
А в § 26 найдем определение веса. Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Масса измеряется в килограммах, а вес в ньютонах.
Масса – это вещь постоянная. Массу можно изменить, если от тела, например, отломать кусочек. С весом все гораздо сложнее…
В 7 классе, до изучения второго закона Ньютона, в учебнике говорилось, что если тело и опора покоятся или движутся равномерно и прямолинейно, то вес тела равен силе тяжести и определяется по той же формуле:
Но следовало учитывать, что «сила тяжести действует на тело, а значит, приложена к самому телу, а вес действует на опору или подвес, т.е. приложен к опоре».
А в § 2 для дополнительного чтения, мы впервые узнали, что такое невесомость. В состоянии невесомости вес тела равен нулю, а сила тяжести, как и масса тела, нулю не равны.
Удивительно, но в момент прыжка, когда на нас действует только сила тяжести, а сопротивлением воздуха можно пренебречь, то наш вес равен нулю. Можно считать, что мы находимся в невесомости.
А вот в 9 классе в § 11 был введен второй закон Ньютона: ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе.
= 
И поэтому, вес тела – это результат совместного решения двух уравнений, составленных в соответствии со вторым и третьим законами Ньютона.
Если тело лежит на неподвижной опоре относительно Земли, то на тело действуют сила тяжести направленная вертикально вниз, и сила нормального давления или сила реакции опоры. Силы, действующие на тело, уравновешивают друг друга. В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой – весом, равной по модулю силе реакции опоры и направленной в противоположную сторону. Т.е. вес численно равен силе тяжести, это как раз то, о чем мы говорили в 7 классе.
Если же наше тело, будет находиться в лифте, который движется с ускорением, то вес тела может быть больше или меньше силы тяжести. Результат зависит от направления ускорения.
Таким образом, в физике принято строгое различие понятий веса, силы тяжести и массы. С точки зрения физики, приходя на рынок и обращаясь к продавцу, следовало бы говорить: «Дайте, пожалуйста, десять ньютон клубники». Но все уже привыкли к слову вес, как синониму термина «масса».
Но очень важно понимать, что это вовсе не одно и то же!
Однако, массы некоторых тел очень большие. А человеку часто приходится поднимать, двигать тяжелые предметы. С давних пор человек применяет различные вспомогательные приспособления для облегчения своего труда.
В § 55-56 учебника физики для 7 класса мы познакомились с простыми механизмами и в частности – рычагом.
В нашем современном мире рычаги находят широкое применение как в природе, так и в повседневной жизни, созданной человеком. Практически любой механизм, преобразующий механическое движение, в том или ином виде использует рычаги.
С помощью рычагов три тысячи лет назад при строительстве пирамид в Древнем Египте передвигали и поднимали на большую высоту тяжелые каменные плиты.
Рычаги позволяю получить выигрыш в силе!
Рычаги встречаются в разных частях тела человека и животных. Это, например, конечности, челюсти. Много рычагов можно увидеть в теле насекомых и птиц.
Рычаги так же распространены и в быту. Это и водопроводный кран, и дверь, и различные кухонные приборы
Правило рычага лежит в основе действия рычажных весов, различного рода инструментов и устройств, применяемых там, где требуется выигрыш в силе или в расстоянии.
Рычаг – это твёрдое тело, которое может вращаться вокруг точки опоры. Рычаг находится в равновесии, если сумма моментов сил равна нулю. Момент силы – это величина, равная произведению силы на плечо этой силы. M = Fl. Плечо – это кратчайшее расстояние от точки опоры, до линии, вдоль которой действует сила (перпендикуляр).
Различают рычаги 1 рода, в которых точка опоры располагается между точками приложения сил, и рычаги 2 рода, в которых точки приложения сил располагаются по одну сторону от опоры.
Среди рычагов 2 рода выделяют рычаги 3 рода, с точкой приложения «входящей» силы ближе к точке опоры, чем нагрузки, что даёт выигрыш в скорости и пути
Примеры: рычаги первого рода — детские качели (перекладина), ножницы; рычаги второго рода — тачка (точка опоры — колесо), приподнимание предмета ломом движением вверх; рычаги третьего рода — задняя дверь багажника или капот легковых автомобилей на гидравлических телескопических упорах, подъём кузова самосвала (с гидроцилиндром в центре), движение мышцами рук и ног человека и животных.
Рычаги очень часто встречаются в живой природе.
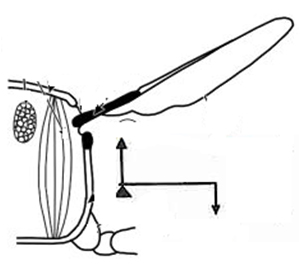
В скелете животных и человека все кости, имеющие некоторую свободу движения, являются рычагами.
Рычажные механизмы скелета в основном рассчитаны на выигрыш в скорости при потере в силе. Особенно большие выигрыши в скорости получаются у насекомых.
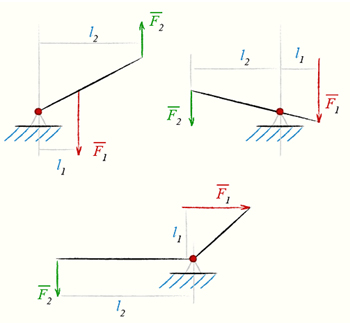
Для осуществления полета крылья должны иметь особое расположение и возможность свободно двигаться. Крыло насекомых можно сравнить с двуплечим рычагом. Короткое плечо представлено его внутренней частью (основанием), которая скрыта под мембраной, а длинное располагается снаружи: собственно, эту видимую часть и принято считать крылом. На внутренней поверхности экзоскелета, сразу под местом сочленения крыла с телом, находится плотный выступ, который называют плейральным столбиком; данная структура играет роль точки опоры при взмахе крыльев.
В скелете животных и человека все кости, имеющие некоторую свободу движения, являются рычагами, например, у человека – кости конечностей, нижняя челюсть, череп, фаланги пальцев.
Однажды я увидела в журнале рисунок, который захотелось использовать для оформления стенгазеты. Но рисунок был очень маленьким, а мне хотелось сохранить масштаб при увеличении его размеров. Я задумалась, как можно увеличить рисунок до нужных размеров. Оказывается, это можно сделать либо вручную «методом клеток», либо с помощью приборов: эпидиаскопа, или пантографа.
Пантограф (название происходит от двух греческих слов (pantos) – все и qrapho – пишу) – прибор в виде раздвижного шарнирного параллелограмма для перерисовки рисунков, чертежей, схем в другом (увеличенном или уменьшенном масштабе). В основе работы этого прибора тоже лежит рычаг. Важной особенностью пантографа является простота его конструкции и очень высокая «точность» скопированного изображения. Но купить пантограф в магазине оказалось делом не простым. Тогда я решила его изготовить самостоятельно.
Пантографы широко используются в технике.
Так одним из основных видов городского транспорта является трамвай. Большинство трамваев используют электротягу с подачей электроэнергии через воздушную контактную сеть с помощью токоприёмников, чаще всего токоприёмник изготовлен в виде пантографов.
Очень часто пантографы используют в мебели. В этом случае пантограф по представляет собой штангу с подъемным механизмом. Обеспечивая легкий доступ к верхнему ярусу, пантограф способствует более эффективному использованию внутреннего пространства шкафа и лучшей организации хранения вещей.
Практическая часть
Прежде чем изготовить пантограф, я изготовила качели – рычаги.
Качели с перемещаемым сиденьем
Всем известны обычные детские качели рычажного типа, когда 2 ребёнка садятся по разным концам качелей и качаются, поочерёдно отталкиваясь от земли ногами. Но дети бывают разного веса. И обычно лёгкий ребёнок сидит наверху, а тяжёлый перевешивает его. Последний должен больше работать ногами, чтобы качели хоть как-то качались. Чтобы уравнять работу обоих, можно сделать перемещаемое сиденье на конструкции качелей. Тогда в зависимости от веса ребёнка подбирается длина рычага и у обоих детей уравниваются возможности и количество отталкиваний от земли в единицу времени.
2 модель:
тяжёлый груз перевешивает ребёнка
3 модель: При перемещении сидения равновесие снова устанавливается
Изготовление пантографа
Воспользовавшись описанием изготовления пантографа с сайта «Мир самоделок»[5] я купила пластмассовые линейки, болты и гайки и изготовила свой пантограф.
Я изготовила анимационный материал, ссылка на который представлена: https://cloud.mail.ru/home/ВавилинаЕА.mkv
Работая над этим материалом, я не только повторила основные законы, определения. Я узнала много нового о рычагах. Изготовила пантограф и научилась его использовать. Изготовила небольшой анимационный материал.
Пожалуй, самое удивительное, это то, что когда я начала свою работу над проектом для участия во Всероссийском заочном конкурсе для обучающихся «Я учу физику», посвящённого 115-летию А.В. Пёрышкина, я не знала что получится. Оказывается, физические явления вокруг нас словно цепляются друг за друга. Так и хочется сказать: «Все взаимосвязано! А физика самая интересная и увлекательная наука!»