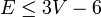Что такое планарный граф
Планарный граф
Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.
Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины — это точки плоскости, а ребра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.
Содержание
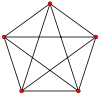
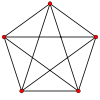
Два примера непланарных графов
Здесь мы пользуемся интуитивным понятием слова «линия», подробнее см. в соответствующей статье.
Полный граф с пятью вершинами
Лемма. Полный граф с пятью вершинами (К5) нельзя уложить на плоскость.
«Домики и колодцы»
Задача о трёх колодцах. Есть три дома и три колодца. Можно ли так проложить дорожки между домами и колодцами, чтобы от каждого дома к каждому колодцу вела дорожка, и никакие две дорожки не пересекались бы. Мосты строить нельзя.
Лемма. Полный двудольный граф с тремя вершинами в каждой из долей (К3,3) нельзя уложить на плоскость.
Теорема Понтрягина-Куратовского
Очевидно утверждение: если граф G содержит подграф, гомеоморфный K5 или K3,3, его невозможно разложить на плоскости. Оказывается, верно и обратное.
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных полному графу из пяти вершин (K5) или графу «домики и колодцы» (K3,3).
Теорему также можно сформулировать в следующем варианте (иногда его называют «теорема Вагнера»).
Граф планарен тогда и только тогда, когда не содержит подграфов, стягивающихся в K5 или K3,3.
Признаки непланарных графов
Формула Эйлера
Для связного плоского графа справедливо следующее соотношение между количеством вершин 


Оно было найдено Эйлером в 1736 г. [1] при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариант поверхности, для плоскости или сферы он равен двум. Формула имеет множество полезных следствий. Если каждая грань ограничена не менее чем тремя ребрами (при условии, что в графе больше двух ребер), а каждое ребро разделяет две грани, то
то есть, при большем числе ребер такой граф заведомо непланарен. Обратное утверждение не верно, например, граф Петерсена. Отсюда следует, что в планарном графе всегда можно найти вершину степени не более 5.
Планарные графы в задачах
Раскраска карты. Необходимо раскрасить плоскую карту заданным числом красок так, что любые две страны, имеющие общий участок границы, имели различные цвета. Оказывается, что при отсутствии анклавов, всегда достаточно четырех красок, но это утверждение чрезвычайно сложно доказать, см. Проблема четырёх красок.
Спрямление графа. Любой плоский граф можно перерисовать так, чтобы он остался плоским, а рёбра стали прямолинейными.
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Планарный граф» в других словарях:
планарный граф — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN planar graph … Справочник технического переводчика
ГРАФ ПЛОСКИЙ — планарный граф, граф, допускающий правильную укладку на плоскости (см. Графа укладка). Иными словами, граф G наз. плоским, если он может быть изображен на плоскости так, что вершинам соответствуют различные точки плоскости, а линии,… … Математическая энциклопедия
Граф Петерсена — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
Плоский граф — Планарный граф граф, который может быть изображен на плоскости без пересечения ребер. Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его … Википедия
Вершина (граф) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
плоский граф — планарный граф — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы планарный граф EN flat graph … Справочник технического переводчика
Двудольный граф — Биграф Двудольный граф или биграф это математический термин теории графов, обозначающий граф, множество вершин которого можно разбить на две части таким образом, что ка … Википедия
Планарность — Планарный граф граф, который может быть изображен на плоскости без пересечения ребер. Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его … Википедия
Теория графов — Граф с шестью вершинами и семью рёбрами Теория графов раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строго … Википедия
Гамма-алгоритм — Гамма алгоритм алгоритм плоской укладки графа и проверки его на планарность. Содержание 1 Определения 2 Алгоритм 3 Реализация … Википедия
Планарность
Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.
Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины это точки плоскости, а ребра линии на ней, области, на которые граф разбивает поверхность называются гранями. Плоский граф — граф уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.
Содержание
Критерий непланарности
Теорема Понтрягина-Куратовского
Граф планарен тогда и только тогда, когда не содержит подграфов, гомеоморфных K5 или K3,3.
Граф планарен тогда и только тогда, когда он не содержит подграфов, стягиваемых в K5 или K3,3.
Формула Эйлера
Для связного плоского графа справедливо следующее соотношение между количеством вершин V, ребер E и граней F:
Оно было найдено Эйлером в 1736 г. [1] при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариант поверхности, для плоскости или сферы он равен двум.
Формула имеет множество полезных следствий. Из того, что каждая грань ограничена не более чем тремя ребрами, следует, что для плоского графа
то есть, при большем числе ребер граф заведомо непланарен. (Обратное утверждение не верно, пример.) Отсюда следует, что в планарном графе всегда можно найти вершину степени не более 5.
Планарные графы в задачах
Задача о трех колодцах. Есть три дома и три колодца. Доказать, что невозможно так проложить дорожки между домами и колодцами, чтобы от каждого дома к каждому колодцу вела дорожка, и никакие две дорожки не пересекались бы. (Мосты строить нельзя.)
Раскраска карты. Необходимо раскрасить плоскую карту заданным числом красок так, что любые две страны имеющий общий участок границы имели различные цвета. Оказывается, что при отсутствии анклавов, всегда достаточно четырех красок, но это утверждение чрезвычайно сложно доказать, см. Проблема четырёх красок.
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Планарность» в других словарях:
Киприанов, Андрей Иванович — [р. 4 (16) июля 1896] сов. химик органик, акад. АН УССР (с 1945). В 1919 окончил Харьков. ун т, где работал до 1941 (с 1940 проф.). С 1944 проф. Киев. ун та; одновременно (с 1945) дир. Ин та органич. химии АН УССР. Осн. работы выполнены в области … Большая биографическая энциклопедия
ИНТЕГРАЛЬНАЯ СХЕМА — твердотельное устройство, содержащее группу приборов и их соединения (связи), выполненное на единой пластине (подложке). В И. с. интегрируются пассивные элементы (ёмкости, сопротивления) и активные элементы, действие к рых основано на разл. физ.… … Физическая энциклопедия
ГИПЕРГРАФ — обобщение понятия графа. Г. задается множеством V, элементы к рого наз. вершинами, и семейством подмножеств множества V, называемых ребрами Г.; Г. обозначается Понятие Г. является вариантом давно известных понятий комплекса, блок схемы, а также… … Математическая энциклопедия
Теория графов — Граф с шестью вершинами и семью рёбрами Теория графов раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строго … Википедия
Планарный граф — Планарный граф граф, который может быть изображен на плоскости без пересечения ребер. Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим … Википедия
Гамма-алгоритм — Гамма алгоритм алгоритм плоской укладки графа и проверки его на планарность. Содержание 1 Определения 2 Алгоритм 3 Реализация … Википедия
Гипотеза Хадвигера — Не следует путать с проблемой Нелсона Эрдеша Хадвигера. Гипотеза Хадвигера одна из неразрешённых гипотез теории графов. Она формулируется следующим образом: всякий k хроматический граф стягиваем к полному графу на вершинах.… … Википедия
Система графов — Системой графов является такая совокупность или множество графов, где между элементами зафиксировано соотношение. Графы систематизируются исходя из характеристик, чаще всего, таких как планарность, регулярность, транзитивность и т.д. Большая… … Википедия
СОДЕРЖАНИЕ
Теоремы Куратовского и Вагнера
Вместо того, чтобы рассматривать подразделения, теорема Вагнера имеет дело с несовершеннолетними :
Минор графа результатов принимать подграф и неоднократно стягивание края в вершину, с каждым соседом исходных конечных вершин становится соседом новой вершины.
Другие критерии планарности
На практике трудно использовать критерий Куратовского, чтобы быстро решить, является ли данный граф плоским. Однако существуют быстрые алгоритмы решения этой проблемы: для графа с n вершинами можно определить за время O ( n ) (линейное время), может ли граф быть плоским или нет (см. Проверка планарности ).
Для простого связного плоского графа с v вершинами, e ребрами и f гранями для v ≥ 3 выполняются следующие простые условия :
Формула Эйлера
Средняя степень
Графики монет
Плотность планарного графика
Связанные семейства графов
Максимальные плоские графы
Внешнепланарные графы
Графики Халина
Другие родственные семьи
Перечисление планарных графов
Почти все плоские графы имеют экспоненциальное число автоморфизмов.
Другие факты и определения
Теорема о четырех цветах утверждает, что каждый планарный граф можно раскрашивать в четыре цвета (т. Е. С четырьмя частями).
Двойственные полезны, потому что многие свойства двойственного графа связаны простыми способами со свойствами исходного графа, что позволяет доказывать результаты о графах, исследуя их двойственные графы.
Хотя дуальный, построенный для конкретного вложения, уникален (с точностью до изоморфизма ), графы могут иметь разные (т. Е. Неизоморфные) дуальные, полученные из разных (т. Е. Негомеоморфных ) вложений.
Теорема о плоском разделителе утверждает, что любой планарный граф с n вершинами можно разбить на два подграфа размером не более 2 n / 3 путем удаления O ( √ n ) вершин. Как следствие, планарные графы также имеют ширину дерева и ширину ветвления O ( √ n ).
Для двух плоских графов с v вершинами можно определить за время O ( v ), изоморфны они или нет (см. Также проблему изоморфизма графов ).
Представимые в виде слов плоские графы включают в себя плоские графы без треугольников и, в более общем смысле, трехцветные плоские графы, а также определенные подразделения граней треугольных сеточных графов и определенные триангуляции покрытых сеткой цилиндрических графов.
Планарный график
СОДЕРЖАНИЕ
Теоремы Куратовского и Вагнера [ править ]
Вместо того, чтобы рассматривать подразделения, теорема Вагнера имеет дело с несовершеннолетними :
Минор графа результатов принимать подграф и неоднократно стягивание края в вершину, с каждым соседом исходных конечных вершин становится соседом новой вершины.
Другие критерии планарности [ править ]
На практике трудно использовать критерий Куратовского, чтобы быстро решить, является ли данный граф плоским. Однако существуют быстрые алгоритмы решения этой проблемы: для графа с n вершинами можно определить за время O ( n ) (линейное время), может ли граф быть плоским или нет (см. Проверка планарности ).
Для простого связного плоского графа с v вершинами, e ребрами и f гранями для v ≥ 3 выполняются следующие простые условия :
Формула Эйлера [ править ]
Средняя степень [ править ]
Графики монет [ править ]
Плотность планарного графика [ править ]
Связанные семейства графиков [ править ]
Максимальные планарные графики [ править ]
Внешнепланарные графики [ править ]
Графики Халина [ править ]
Другие родственные семейства [ править ]
Перечисление плоских графов [ править ]
Почти все плоские графы имеют экспоненциальное число автоморфизмов. [9]
Другие факты и определения [ править ]
Теорема о четырех цветах утверждает, что каждый плоский граф 4- раскрашиваем (т. Е. 4-долен).
Двойственные полезны, потому что многие свойства двойственного графа связаны простыми способами со свойствами исходного графа, что позволяет доказывать результаты о графах, исследуя их двойственные графы.
Хотя двойственный, построенный для конкретного вложения, уникален (с точностью до изоморфизма ), графы могут иметь разные (т. Е. Неизоморфные) двойственные, полученные из разных (т. Е. Негомеоморфных ) вложений.
Теорема о плоском разделителе утверждает, что любой планарный граф с n вершинами может быть разбит на два подграфа размером не более 2 n / 3 путем удаления O ( √ n ) вершин. Как следствие, планарные графы также имеют ширину дерева и ширину ветвления O ( √ n ).
Для двух плоских графов с v вершинами можно определить за время O ( v ), изоморфны они или нет (см. Также проблему изоморфизма графов ). [11]
Представимые в виде слов плоские графы включают плоские графы без треугольников и, в более общем смысле, трехцветные плоские графы, [13], а также некоторые подразделения граней треугольных сеточных графов [14] и некоторые триангуляции покрытых сеткой цилиндрических графов. [15]
Гамма-алгоритм
| Задача: |
| Определить, является ли граф планарным, и, если да, произвести его плоскую укладку. |
Чтобы проверить планарность графа и произвести его плоскую укладку, удобно пользоваться гамма-алгоритмом.
Содержание
Входные данные [ править ]
На вход алгоритму подаются графы со следующими свойствами:
Если нарушено свойство 1, то граф нужно укладывать отдельно по компонентам связности. Если нарушено свойство 2, то граф — дерево и нарисовать его плоскую укладку тривиально.
Более подробно рассмотрим случай, когда в графе [math]G[/math] нарушено свойство 3. Сначала все мосты нужно убрать, далее произвести отдельную укладку всех компонент следующим образом: уложим одну компоненту связности, а следующую компоненту, связанную с первой в графе [math]G[/math] мостом, будем рисовать в той грани, в которой лежит вершина, принадлежащая мосту. Иначе может сложиться ситуация, когда концевая вершина моста будет находиться внутри плоского графа, а следующая компонента — снаружи. Таким образом мы сможем соединить мостом нужные вершины. Далее будем так поступать с каждой новой компонентой.
Описание алгоритма [ править ]
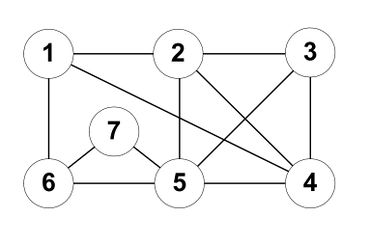
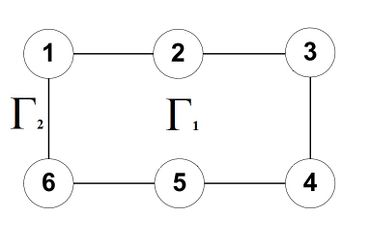
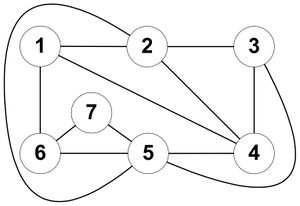
Рассмотрим работу алгоритма, параллельно разбирая на примере каждый шаг. Пусть дан граф [math]G[/math] (рис. 1).
Инициализация [ править ]
Первый этап — инициализация алгоритма.
Общий шаг [ править ]
Второй этап — общий шаг.
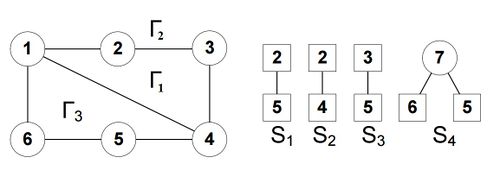
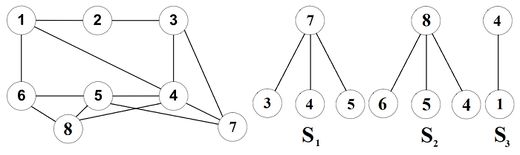
Построим множество сегментов. Каждый сегмент [math]S[/math] относительно уже построенного [math]G_
Вершины, одновременно принадлежащие [math]G_
Пусть в каком-то сегменте нет ни одной контактной вершины. В таком случае граф до выделения [math]G_
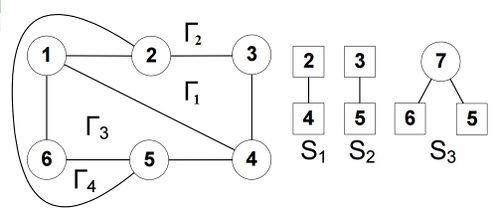
Третий и последующие этапы аналогичны второму. Повторять вышеуказанные действия нужно либо до тех пор, пока не будет получена плоская укладка, то есть множество сегментов не останется пустым, либо пока не будет получено, что граф не планарен.
Опишем алгоритм коротко и формально:
Доказательство корректности гамма-алгоритма [ править ]
Перед доказательством корректности приведем ряд важных вспомогательных лемм.
Пусть два сегмента [math]S_<1>[/math] и [math]S_<2>[/math] называются конфликтующими относительно уже уложенной части, если:
| Определение: |
| Частичной укладкой [math]G'[/math] планарного графа [math]G[/math] называется граф, который можно получить из какой-либо укладки графа [math]G[/math] на плоскости путем удаления некоторых ребер и вершин. |
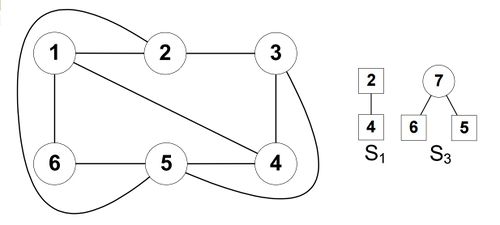
Например, для графа на рис. 1 служебный граф будет иметь вид (рис. 2):
Докажем индукцией по числу шагов.
Таким образом, на каждом шаге мы получаем частичную укладку графа, что доказывает корректность гамма-алгоритма.[math]\triangleleft[/math]
Следствие: Если граф [math]G[/math] планарный, то гамма-алгоритм строит его плоскую укладку.