Что такое периодичность тангенса
Что такое периодичность тангенса
ЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
Четность тригонометрических функций.
Углы φ и —φ образуются при повороте луча в двух взаимно противоположных направлениях (по часовой стрелке и против часовой стрелки).
Поэтому конечные стороны OA 1 и ОА 2 этих углов симметричны относительно оси абсцисс.
Следовательно, синус является нечетной, а косинус — четной функцией угла.
Поэтому тангенс и котангенс являются нечетными функциями угла.
Выяснить, какие из данных функций являются четными и какие нечетными:
1) у = sin (—х); 4) у = sin x cos х; 7) у = sin 2 x;
2) у = cos (—х); 5) у = sec x; 8) у = cos 2 x;
3) у = tg (2х); 6) у = cosec x; 9) у = sin x + tg x.
Периодичность функций sin φ и cos φ
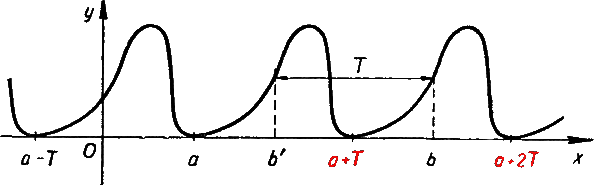
Предположим, что вектор ОА = (х, у) единичной длины образует с осью абсцисс угол φ.
Если сделать полный оборот вектора ОА вокруг точки О против часовой стрелки, то получится угол φ + 360°. Но вектор ОА при этом займет первоначальное положение, а потому координаты его х и у не изменятся.
Эти соотношения показывают, что значения функций sin φ и cos φ не изменяются, если их аргумент, увеличить на 360°.
Пусть f(х) есть некоторое выражение, зависящее от переменной величины х.
(Например, f(х) = x 2 , f(х) = sin x и т. д.)
Определяет у как функцию аргумента х.
Если при любых допустимых значениях аргумента х
где Т — некоторое отличное от нуля число, то функция f (x) называется периодической, а число Т — ее периодом.
Согласно этому определению функции sin x и cos х являются периодическими с периодом Т = 360°.
При n полных оборотах вектора ОА против часовой стрелки образуется угол φ + 360°n, а по часовой стрелке — угол φ — 360°n. В каждом из этих случаев координаты х и у вектора не изменяются, а потому не изменяются sin φ и cos φ.
Таким образом, cos φ = cos (φ + 360°n),
sin φ = sin (φ + 360°n), (1)
где n — любое целое число (положительное, отрицательное или нуль).
Можно доказать, что любая периодическая функция (а не только sin φ и cos φ) имеет бесконечное множество периодов.
Говоря о периоде функции, удобно из бесконечного множества всех ее периодов иметь в виду какой-нибудь один вполне определенный период. Обычно выделяют наименьший положительный период функции.
Из всех рассмотренных выше периодов функции sin φ наименьшим положительным периодом является угол в 360°. Но, может быть, существует еще меньший угол, который мы просто упустили из виду, но который, Также является периодом функции sin φ? Чтобы решить этот вопрос, предположим, что наименьший положительный период функции sin φ равен Т. Тогда при любом φ
В частности, при φ = 0 получаем: sinТ = sin 0° = 0.
Составляет ли он период функции sin φ? Если бы это было так, то равенство sin (φ + 180°) = sin φ должно было бы выполняться при всех значениях φ. В частности, при φ = 90° мы получили бы
Аналогично можно доказать, что периодом функции cos φ также является угол в 360° Предлагаем учащимся убедиться в этом самостоятельно.
1. Доказать следующие соотношения:
а) sin 740° = sin 20°; в) cos 54° = cos (—1026°);
б) sin (—1000°) = sin 80°; г) cos (—1750°) = cos 50°.
2. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 360°:
a) sin 820°; б) cos (—7363°); в) sin (—600°).
3. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 180°:
a) cos 729°; б) sin 1268°; в) sin (— 535°); г) cos (— 1001°).
4. Доказать, что угол в 540° является одним из периодов функции у = cos2х.
5. Доказать, что угол и 360° является одним из периодов функции у = tgx.
6. Докажите, что любой период Т функции у = cos х является корнем уравнения
Верно ли обратное утверждение?
Периодичность функций tg φ и ctg φ
Следовательно, при любом φ
Это означает, что функция tg φ является периодической с периодом 180°. Но будет ли угол в 180° наименьшим жительным периодом этой функции?
Предположим, что наименьший положительный период функции tg φ равен Т. Тогда для всех допустимых значений φ должно быть
В частности, при φ = 0° получаем:
Но тангенс положительного угла равен нулю лишь тогда, когда синус этого угла равен нулю, то есть при Т = 180°, 360°, 540° и т, д. Следовательно, никакой положительный угол, меньший 180°, не может быть периодом функции tg φ. Остается признать, чтб периодом (то есть наименьшим положительным периодом) функции tg φ является угол в 180°.
Аналогично можно доказать, что периодом функции сtg φ также является угол в 180°. Предлагаем учащимся убедиться в этом самостоятельно.
1. Данные выражения преобразовать так, чтобы входящие в них углы были положительными и не превышали 180°:
a) tg 205°; б) tg (—185°); в) ctg 300°; г) ctg (—210°).
2. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 90°:
3. Доказать, что угол в 120° является одним из периодов функции у = ctg 3х.
4. Доказать, что любой период Т функции у = ctg х является корнем уравнения
Верно ли обратное утверждение?
О периодических функциях.
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой.
Действительно, пусть периодическая функция f(x) задана в интервале (а, а + Т), где Т — период этой функции.
Покажем, как можно определить значения этой функции в интервале ( а + Т, а + 2 T ).
Для любой точки b из этого интервала можно указать точку b‘ из интервала (а, а + T ), отстоящую от b на расстоянии T.
В силу периодичности функции f(x)
Таким образом, по заданным значениям функции f
Итак, задание периодической с периодом Т функции f(x) на любом интервале длины Т дает возможность полностью охарактеризовать ее на всей числовой прямой. Поэтому для исследования функции f(x), периодической с периодом Т, достаточно изучить ее поведение лишь на каком-нибудь интервале длины Т. Например, для исследования функций у = sin φ и у = cos φ достаточно рассмотреть их лишь при 0° <φ <360°. Для исследования функции у = tg φ можно было бы ограничиться интервалом 0° <φ <180°. Но при φ = 90° tg φ не определен. Поэтому в данном случае целесообразнее выбрать какой-нибудь другой интервал, в каждой точке которою функция у = tg φ была бы определена. Мы отдадим предпочтение интервалу —90° < φ < 90°. Однако в принципе можно было бы выбрать, конечно, и интервал 0° <φ <180°. Для изучения функции сtg φ целесообразно выбрать интервал 0° < φ < 180°.
2. Может ли периодическая с периодом Т функция f(x) удовлетворить условию
Если может, то в каком случае? Ответ пояснить примерами.
Уроки математики и физики для школьников и родителей
суббота, 4 сентября 2021 г.
Урок 5. Периодичность тригонометрических функций
Из этого определения сразу следует, что если Т – период функции
– также периоды функций. Значит у периодической функции бесконечно много периодов.
Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом .
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
у = х – [х] , где [х] – целая часть числа. Если к произвольному значение аргумента этой функции добавить 1 , то значение функции от этого не изменится :
Следовательно, при любом значении х
sin (α + 360 ° ) = sin α
Таким образом, функции sin α и cos α от прибавления к аргументу α одного полного оборота ( 2π или 360 ° ) не меняют своих значений.
где k – любое целое число.
Следовательно, функции sin α и cos α – периодические.
Наименьшее положительное число, от прибавления которого к любому допустимому значению аргумента не изменяется значение функции, называется периодом функции.
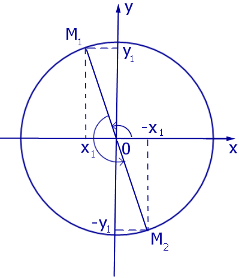
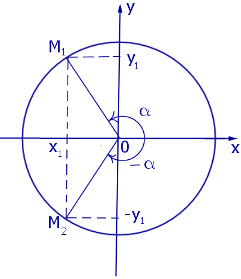
В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным радиусом ОМ единичной окружности.
отсюда следует, что значения tg α и с tg α не изменяются, если к углу α прибавить любое число полуоборотов:
где k – любое целое число.
вычисляются по формуле
равен наименьшему числу, при делении которого на T 1 и T 2 получаются целые числа.
Найти период функции
не существует, так как такого числа, при делении которого на 2π и на 2 получались бы целые числа, нет.
Периода не существует.
Доказать следующее утверждение :
Так как тангенс – периодическая функция с минимальным периодом 20 ∙ 180 ° , то получим :
Доказать следующее утверждение :
Так как косинус – чётная и периодическая функция с минимальным периодом 2π , то получим :
сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.
Доказать следующее утверждение :
Так как синус – нечётная и периодическая функция с минимальным периодом 20 ∙ 360 ° , то получим :
Найти основной период функции
Пусть Т основной период функции, тогда:
так как 2 πk период синуса, то получим :
sin (7х + 7 t ) = sin (7х + 2 πk ),
Найти основной период функции
Пусть Т основной период функции, тогда:
со s 0,3х = со s 0,3(х + t ) = со s (0,3х + 0,3 t )
так как 2 πk период косинуса, то получим :
Найти период функции :
y = 5 sin 2 x + 2 ctg 3х.
Наименьшее число, при делении которого на
Найти период функции :
Находим периоды слагаемых. Период функции
Очевидно, что период заданной функции равен
Найти период функции :
Периода у заданной функции не существует, так как нет такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.
Найти период функции :
Приведём к общему знаменателю периоды :
Тогда наименьшее общее кратное (НОК) будет :
Теперь найдём период заданной функции :
Тригонометрические функции. Понятие периодичности.
Когда точно известно, какой именно угол принимается за единицу измерения, можно говорить об одинаковости масштабов на обеих осях. Тогда число х, измеряющее угол, и число у, выражающее его синус, можно изобразить отрезками, пропорциональными этим числам.
При построении графиков тригонометрических функций обычно принято за единицу измерения угла использовать радиан. Тогда функция у = sin x (под х подразумевается наименование «радианов») изображается графиком, приведенным ниже (масштабы на осях одинаковы). Если за единицу измерения угла принять полрадиана, то, сохраняя те же масштабы, график растянется вдоль оси абсцисс в отношении 2:1.
Линия, являющаяся графиком функции у = sin x, называется синусоидой.
При смещении графика синуса или косинуса на отрезок 2π (вправо или влево) он (график) совмещается сам с собой.
Таким образом, можно сказать, что если график некоторой функции у = f(x) при смещении его на некоторый отрезок вдоль оси абсцисс совмещается сам с собой, то функция называется периодической.
Периодом функции f(x) называется число р, которое измеряет отрезок на оси. Это словесное определение кратко выражается формулой:
Все тригонометрические функции имеют период 2π.
Функции тангенса и котангенса у = tgx и у = ctg х имеют сверх того период π (так как tg (х ± k π) = tg х).
График тангенса у = tg х показан на рисунке.
На рисунке ниже представлен график функции котангенс у = ctg х.
График тангенса неограниченно приближается к прямым, которые параллельны оси ординат и отстоят от нее на расстоянии равном ± π/2, ± 3(π/2), ± 5(π/2) и т.п., но не достигают этих прямых.
Аналогичную роль для графика функции котангенса играют прямые, отстоящие от оси OY на ± π, ±2π, ±3π, и т. д., собственно и сама ось OY.
Свойства тригонометрических функций
Содержание
Знаки тригонометрических функций
определяются тем, в каком квадранте (четверти) координатной плоскости Oxy лежит луч OM (рисунки 1, 2, 3, 4).
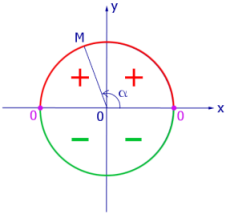 | 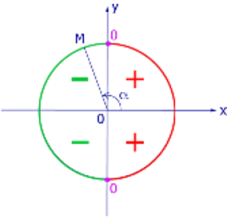 |
| Рис.1. Знак sin α | Рис.2. Знак cos α |
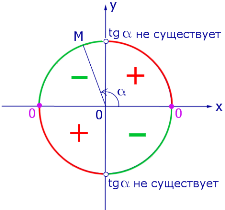 | 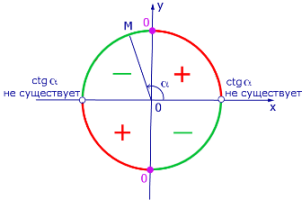 |
| Рис.3. Знак tg α | Рис.4. Знак ctg α |
 |
| Рис.1. Знак sin α |
 |
| Рис.2. Знак cos α |
 |
| Рис.3. Знак tg α |
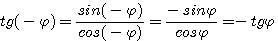
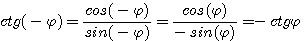














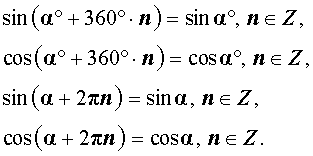


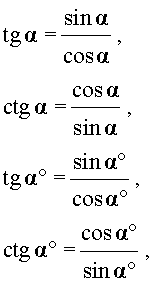

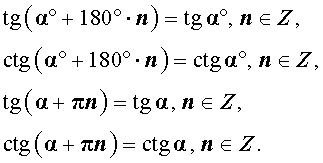


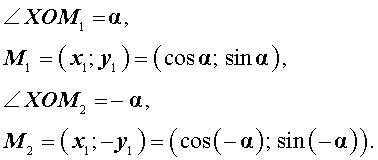






.png)