Что такое пересечение отрезков

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Пересечение отрезков и поворот: определение, свойства, вычисление

Содержание

Аффинное пространство [ править ]

Ориентация [ править ]

Ориентация векторов [ править ]

Из курса линейной алгебры известно, что любые две такие формы отличаются друг от друга только на некоторый множитель. Зафиксируем одну из таких форм (например, считая, что форма равна 1 на наборе из векторов выделенного базиса). Назовем ориентацией набора из N N-мерных векторов знак значения этой формы на этом наборе векторов.

Отметим свойства ориентации:

Неформальное объяснение второго свойства: рассмотрим тройку векторов, таких, что если смотреть из конца первого вектора на второй, то он будет левее, чем третий. Перестановка второго и третьего векторов будет означать, что второй вектор будет виден правее третьего, что означает смену ориентации.

Заметим, что определитель является в точности кососимметричной линейной формой от N N-мерных векторов, а значит, подходит для вычисления ориентации набора векторов.

Ориентация точек [ править ]

Нетрудно заметить, что ориентация набора точек обладает свойствами, похожими на ориентацию векторов:

Предикат левый поворот [ править ]

О точном вычислении ориентации см. раздел Ссылки.

Пересечение отрезков [ править ]

В случае, если обе ориентации в одной из строк равны нулю, отрезки лежат на одной прямой, и в этом случае пересечение можно проверить способом, аналогичным пересечению отрезков на действительной прямой (считаем, что точки сравниваются лексикографически):

Если предикат вычисления ориентации был абсолютно точным, то таким же будет описанный алгоритм.

Источник

Точка пересечения двух отрезков

Введение

Уже не раз на habr затрагивалась данная тема: раз, два.

Я лишь хочу поделиться своей реализацией. Думаю, это кому-то пригодится.

Предупреждаю, данный метод не учитывает некоторые пограничные случаи и вхождение отрезков друг в друга.

Подготовка

Весь последующий код будет приведён на языке Java

Для начала создадим вспомогательный класс Dot. В нём всего две переменные x и y:

Задача 1: определить, касаются ли отрезки.

Решение:
Из векторного произведения мы можем узнать, обхо́дим мы вектор по часовой или против часовой. Это поможет понять где находятся точки. Соединим точки A и D, A и C.

Перемножим вектора main и v2, main и v1. Если полученные произведения имеют разные знаки, значит точки C и D находятся по разные стороны относительно отрезка AB. Назовём такой метод fromDifferentSides:

Таким же образом необходимо проверить точки A и B относительно отрезка CD. Соединим это в один метод и получится следующее:

Задача 2: определить точку касания.

Решение:
Как и в предыдущей задаче определяем, касаются ли отрезки. Если касаются, начинаем определять эту точку. Через подобие найдём длину DO. Коэффициент подобия (k) равен отношению уже известных нам векторных произведений:

В третей строчке проверяем пограничный случай. Теперь узнаем чему равно DO. Для этого решим систему уравнений:

DO = CO*k
Подставляем во второе уравнение:
CO*k+CO = CD
CO(k+1)= CD
CO = CD/(k+1)
В итоге:
DO = (CD/(k+1))*k

Теперь создаём вектор CD и уменьшаем его до длинны DO. Но поскольку мы будем его умножать, нужно взять обратное от (k+1)*k:

Теперь осталось добавить вектор к точке D:

Вот и всё! Мы получили заветную точку.

Предупреждаю, данный метод не учитывает некоторые пограничные случаи и вхождение отрезков друг в друга.

Функцию нахождения точки я назвал pointOfIntersection. Привожу полный код на Java:

Источник

Нахождение точки пересечения двух прямых (и отрезков)

Введение

Довольно часто при разработке игр возникает необходимость находить точку пересечения прямых, отрезков, лучей и т.д. О том, как реализовать это максимально простым способом, в этой статье.

Популярные способы и их критика

Возможно, многие вспомнят способ из школьной алгебры — составить уравнения двух прямых, приравнять их правые части, найти x, и подставить его в уравнение прямой, чтобы найти y (Подробнее здесь).

Однако данный способ становится достаточно громоздким при написании кода (возможно поэтому вы сейчас читаете эту статью), к тому же, он не является универсальным: если одна из прямых параллельна оси Y, мы получим ошибку деления на ноль при вычислении углового коэффициента, и нам придётся прописать код на этот случай; если две прямые перпендикулярны осям, требуется повозиться с обработкой и этого случая. Такой код становится длинным и некрасивым.

В поисках более элегантного решения данной проблемы я наткнулся на весьма интересные способы, основанные на векторном умножении ( habr.com/ru/post/267037 ) и ray castinging’е ( ru.wikipedia.org/wiki/Ray_casting#Концепция ). Но на мой взгляд, они неоправданно сложные в вычислительном плане. Поэтому представляю вашему вниманию (и критике) мой способ.

Мой способ

Задача

Даны координаты двух отрезков. Нужно узнать, пересекаются ли отрезки, и если да, в какой точке. Для этой цели напишем функцию.

Решение

Условные обозначения для исключения недопониманий: a — вектор a, a(y) — проекция вектора a на ось Y, a — вектор a, заданный координатами x1,y1.

Представим наши отрезки в виде двух векторов: a и b. Обратите, внимание, что вектор b имеет противоположное от ожидаемого направление. Введём вектор c. Заметим, что a*k+b*n=c, где k,n — некоторые коэффициенты. Таким образом, получаем систему уравнений:

a(x)*k+b(x)*n=c(x)
a(y)*k+b(y)*n=c(y)
Наша задача сводится к нахождению этих коэффициентов (правда сказать, достаточно найти лишь один из них).

Внимательный читатель заметит, что при a(y)=0, мы получим ошибку. Пропишем ветвление на этапе нахождения a(y). Этот случай ещё проще, ведь мы сразу получаем уравнение с одной неизвестной.

Рекомендую попробовать вывести n самостоятельно, так будет понятнее, что откуда берётся в коде ниже.

Зная n, можно найти точку пересечения, для этого мы отнимем от координаты точки (x3,y3) вектор b*n

Собираем воедино

Данная функция принимает координаты вершин и возвращает значение 1, если прямые отрезков (именно прямые) пересекаются, иначе 0. Если же вам нужны координаты вершин, вы сможете взять их из массива dot[].

Важно: при введении двух совпадающих прямых, алгоритм выводит отсутствие пересечения. Алгоритм находит точку пересечения прямых, на которых лежат отрезки, поэтому точка может оказаться за пределами отрезка (что вам придётся дополнительно проверить в уже своём коде).

Источник

Урок 32. Пересекаются ли два отрезка?

Урок из серии «Геометрические алгоритмы»

Здравствуйте, дорогой читатель. Напишем еще три новые функции.

Функция LinesCross() будет определять, пересекаются ли два отрезка. В ней взаимное расположение отрезков определяется с помощью векторных произведений. Для вычисления векторных произведений напишем функцию — VektorMulti().

Функция RealLess() будет использоваться для реализации операции сравнения «

Задача1. Два отрезка заданы своими координатами. Составить программу, которая определяет, пересекаются ли эти отрезки, не находя точку пересечения.

Решение
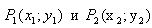
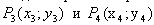
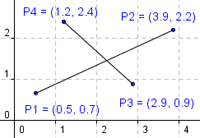
Пусть даны два отрезка. Первый задан точками . Второй задан точками .

Взаимное расположение отрезков можно проверить с помощью векторных произведений:

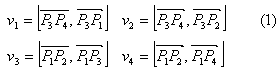
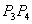
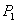
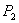
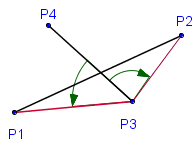
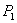
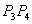
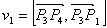
Рассмотрим отрезок и точки и .

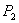
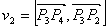
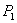
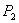
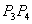
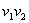
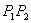
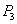
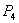
Точка лежит слева от прямой , для нее векторное произведение > 0, так как векторы положительно ориентированы.

Точка расположена справа от прямой, для нее векторное произведение и , лежали по разные стороны от прямой , достаточно, чтобы выполнялось условие и точек и .

Итак, если 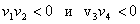, то отрезки пересекаются.

Для проверки этого условия используется функцию LinesCross(), а для вычисления векторных произведений – функция VektorMulti().

Векторное произведение двух векторов вычисляется по формуле:

ax, ay — координаты первого вектора,

bx, by — координаты второго вектора.

Результаты выполнения программы:

Мы написали программу, определяющую, пересекаются ли отрезки, заданные своими координатами.

На следующем уроке мы составим алгоритм, с помощью которого можно будет определить, лежит ли точка внутри треугольника.

Уважаемый читатель. Вы уже познакомились с несколькими уроками из серии «Геометрические алгоритмы». Все ли доступно написано? Я буду Вам очень признательна, если Вы оставите отзыв об этих уроках. Возможно, что-то нужно еще доработать.

Источник