Что такое переместительное и сочетательное свойство сложения
Свойства сложения и вычитания
Свойства (или законы) арифметических действий на числовых примерах мы рассматривали в теме «Законы арифметики» для начальной школы.
В 5 классе законы арифметики записываются с помощью буквенных выражений. Поэтому теперь мы рассмотрим эти и другие свойства в виде буквенных выражений.
Свойства сложения
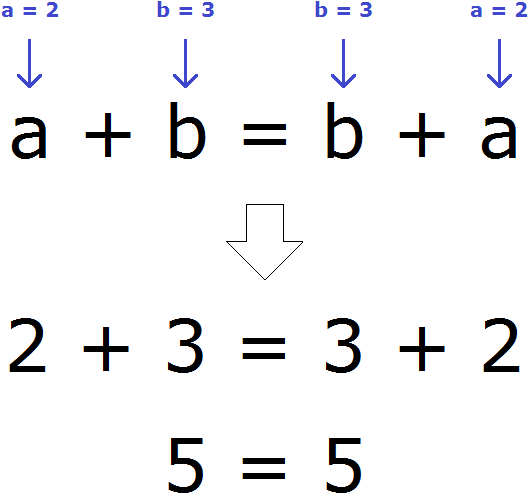
Переместительное свойство сложения
От перестановки слагаемых сумма не меняется.
В буквенном виде свойство записывается так:
Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.
Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто « a + b + с ».
Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.
При сложении нескольких чисел их можно как угодно объединять в группы и переставлять.
Свойство нуля при сложении
Сумма двух натуральных чисел всегда больше каждого из слагаемых. Но это не так, если хотя бы одно из слагаемых равно нулю.
Если к числу прибавить нуль, получится само число.
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.
Скобки в выражении « (a − b) − c » не имеют значения и их можно опустить.
Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
Если из числа вычесть само число, то получится нуль.
Свойства сложения
Содержание
Мы уже умеем складывать числа с помощью рисунка и координатного луча. Умеем складывать однозначные числа, такие как 7 и 5, и многозначные, такие как 123 и 456.
Для того чтобы складывать числа было легче, существует несколько простых правил. Их еще называют законами сложения или свойствами.
Закон – это что-то, что никогда не меняется, и что можно применять для всех чисел.
Заучивать законы сложения не нужно, их нужно только один раз понять и научиться использовать в примерах и задачах. Сделать это очень просто. Сейчас мы сможем в этом убедиться.
Переместительное свойство
Первый закон сложения называется переместительным законом сложения. Звучит он так:
От перестановки слагаемых сумма не меняется.
Чтобы понять этот закон, мы решим один и тот же пример двумя способами.
А теперь поменяем наши числа местами и посчитаем ответ:
Результаты сложения получились одинаковыми. Но заметим, что во втором случае посчитать было гораздо проще, не так ли? Значит, проще было поменять числа местами и потом посчитать.
Сложение с нулем
В корзине было 100 яблок, туда положили 0 яблок, сколько яблок стало в корзине?
Очевидно, что если в корзину не положили яблок, то количество яблок в ней не изменилось, то есть по-прежнему равно 100.
От прибавления нуля число не изменяется
$10+0 = 10$
$0 + 8 = 8$
$0 + 0 = 0$
Сочетательное свойство
В некоторых примерах бывает нужно сложить не два числа, а несколько.
Складываем все числа слева направо привычным для нас способом. Получаем:
Если мы внимательно посмотрим на числа, то сможем увидеть, что легче сначала сложить 4 и 6, а затем к полученной сумме прибавить и число 29.
$29 + 4 + 6 = 24 + 10 = 39$
Ответ получился таким же.
Значит, при сложении нескольких чисел можно складывать сначала те числа, которые нам удобнее сложить. А затем уже к полученной сумме прибавляем оставшиеся числа. Мы, так сказать, сочетаем те числа, которые легче посчитать при сложении.
Этот закон называется сочетательный закон сложения. Кратко он звучит так:
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
Законы сложения можно применять при сложении не только двух или трех, но и большего количество чисел.
Чтобы решить этот пример, посмотрим внимательно на числа. Заметим, что легче всего было бы сложить 128 и 12, а к числу 383 легче прибавить 17. Поэтому мы сейчас поменяем местами числа 17 и 12. То есть применим в нашем примере переместительный закон. Получим:
Теперь группируем попарно числа, которые будем складывать. То есть применим сочетательный закон. Для этого мы используем скобки:
Считаем, сколько получится в скобках и складываем результаты:
Вот так легко и быстро мы получили ответ, применяя законы сложения.
Законы математики
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
Запишем сочетательный закон сложения с помощью переменных:
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
Запишем переместительный закон умножения с помощью переменных:
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
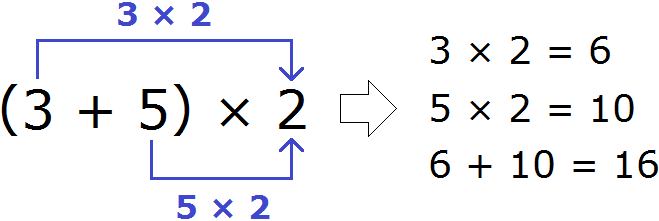
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
Свойства сложения и вычитания
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
При этом саму запись (2 + 5) можно тоже назвать суммой.
Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
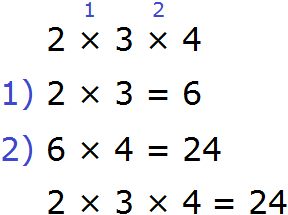
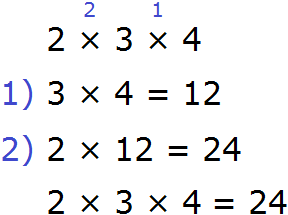
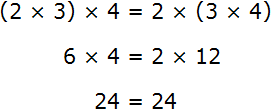
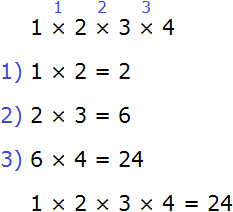
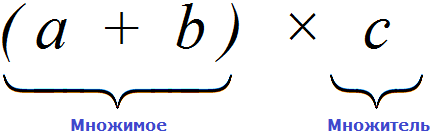
Числа 3 и 4, которые мы сложили называется слагаемыми. А результат сложение число 7 называется суммой.
В буквенном виде этот пример будет выглядеть так:
Второй вариант таблицы сложения.
Если посмотрим на таблицы сложения, видно как работает переместительный закон.